أثناء عملية إنشاء رسم تطوير مكوّن الصفائح المعدنية، من الضروري أيضًا مراعاة تأثير سُمك مادة المعالجة، أي إجراء تعديلات مناسبة على سُمك اللوحة.
بشكل عام، بالنسبة لمواد الصفيحة التي يقل سمكها عن 3 مم، لا يلزم تعديل سمك الصفيحة. يمكن حسابها وفقًا للقطر المركزي لمادة الصفيحة أو وفقًا لخطوط القطع الداخلية والخارجية للسطح الداخلي والخارجي. تكون الأبعاد بعد التشكيل ضمن نطاق الانحراف المسموح به. عندما تكون سماكة الصفيحة أكبر من 3 مم، يجب حسابها وفقًا للقطر المركزي لمادة الصفيحة. ولتسهيل الوصف، تشير الحسابات الخاصة بالمواد المطورة التالية إلى القطر المركزي لمادة الصفيحة.
1. حساب تطوير الأصداف الأسطوانية
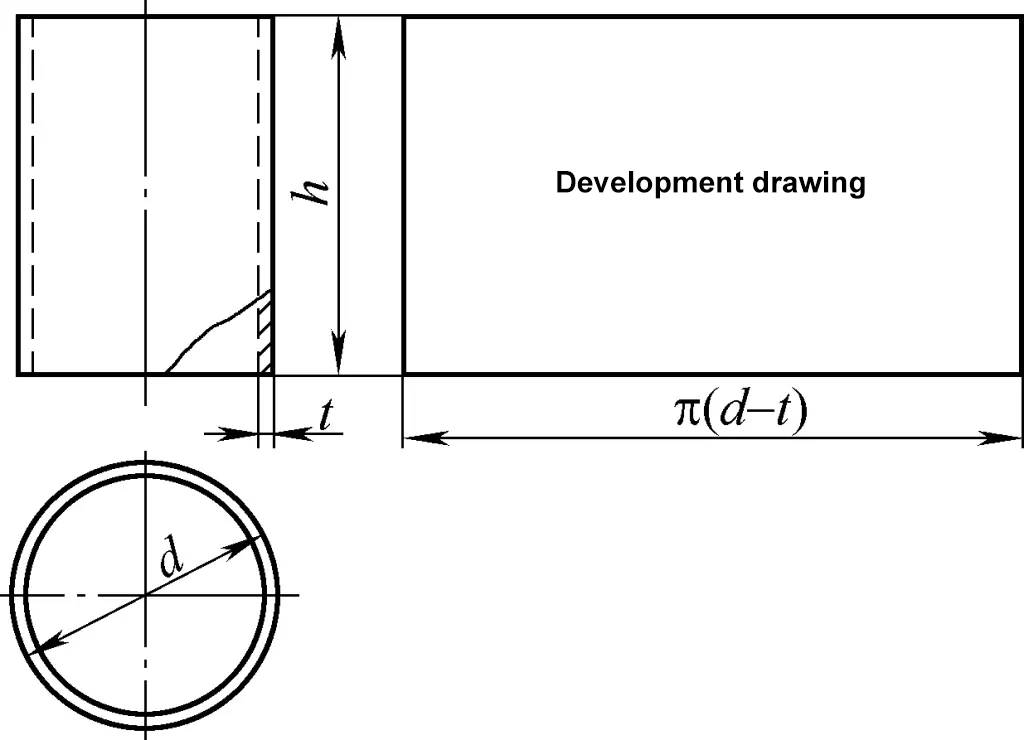
تنتمي القشرة الأسطوانية إلى السطح الأسطواني، ورسم تطورها عبارة عن مستطيل. أحد ضلعي المستطيل يساوي محيط الأسطوانة π (d-t)، والضلع الآخر هو ارتفاع الأسطوانة h، كما هو موضَّح في الشكل 1. في الشكل، d هو القطر الخارجي للأسطوانة و t هو سُمك الصفيحة.
2. حساب تطوير المخروط الدائري الأيمن
الرسم التطويري للمخروط الدائري الأيمن عبارة عن قوس قطاعي. الصيغة الحسابية لرسم تطوير المخروط الدائري الأيمن الموضَّح في الشكل 2 هي
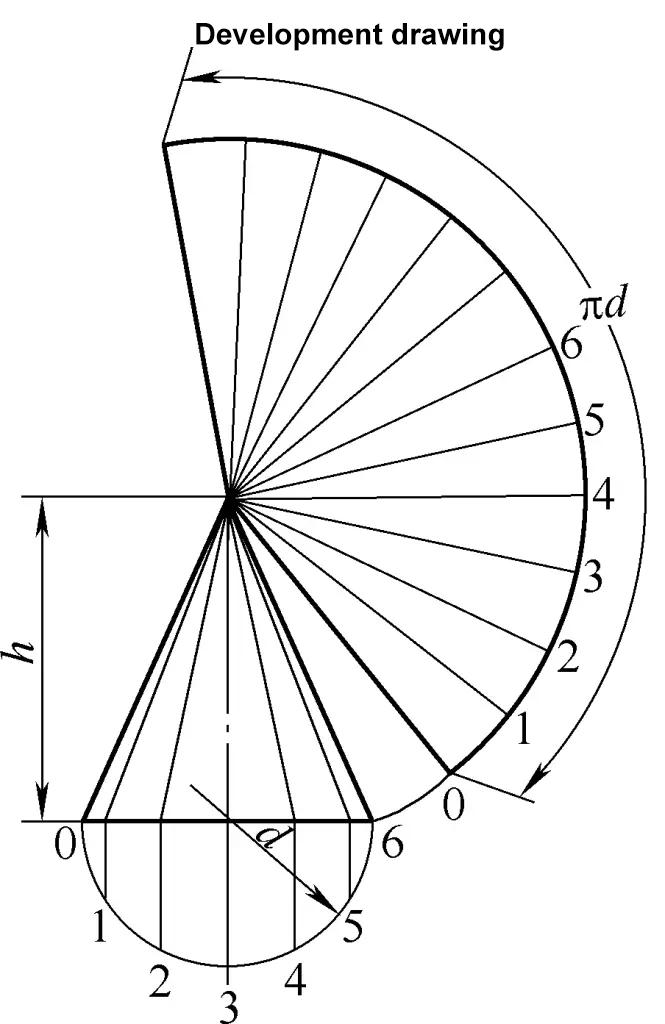
R=1/2√(d2+4h2)
α=180 د/180/د/ر
ل=2ص=2رسين ألفا/2
في الصيغة
- R - نصف قطر قوس القطاع (مم);
- α - زاوية القطاع (°);
- L - طول وتر قوس القطاع (مم).
3. حساب تطوير المخروط الدائري الأيمن المقطوع
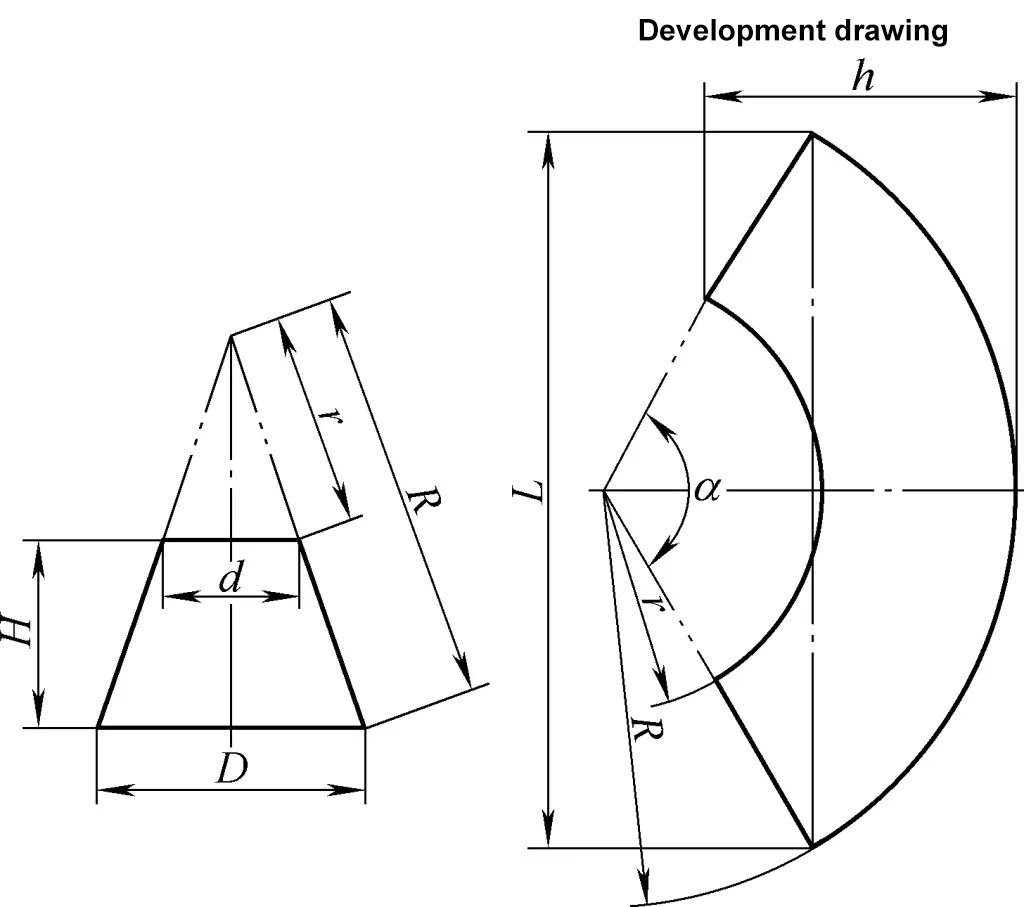
إن الرسم التطويري للمخروط الدائري القائم المقطوع هو قوس قطاعي متحد المركز. الصيغة الحسابية لرسم تطوير المخروط الدائري القائم المبتور المقطوع الموضَّح في الشكل 3 هي
R=√{(D/2)2+[د.د/(د-د)]2}
ص=د/د/د
α=180د/180/ص
ل=2ص=2رسين ألفا/2
ح=ص-ر-ركوس ألفا/2
عندما تكون α>180°، h=R+R+rsin[(α-180)/2]
لمعرفة معاني الرموز في الصيغة، راجع الشكل 3.
4. حساب تطور المخروط الدائري المائل الأيمن المائل
الرسم التطويري للمخروط الدائري المائل القائم المائل هو قوس قطاع غير منتظم. الصيغة الحسابية لرسم تطوير المخروط الدائري الأيمن المائل الموضح في الشكل 4 هي
تان1= h/[1/2(D1-d1)+l]
تان2= ح/[1/2(د1-D1)+l]
د=د1-t/2 (sinβ1+ sinβ2)
د=د1-t/2 (sinβ1+ sinβ2)
أ=دال/(د-د)
ح=آه/لتر
fn=√[(أ-د/2ج/ج/جوس ألفاn)2+(D/2)2الخطيئة2αn+H2]
yn=fn(1-ح/ح/ح)
m=Dsin(180°/n )
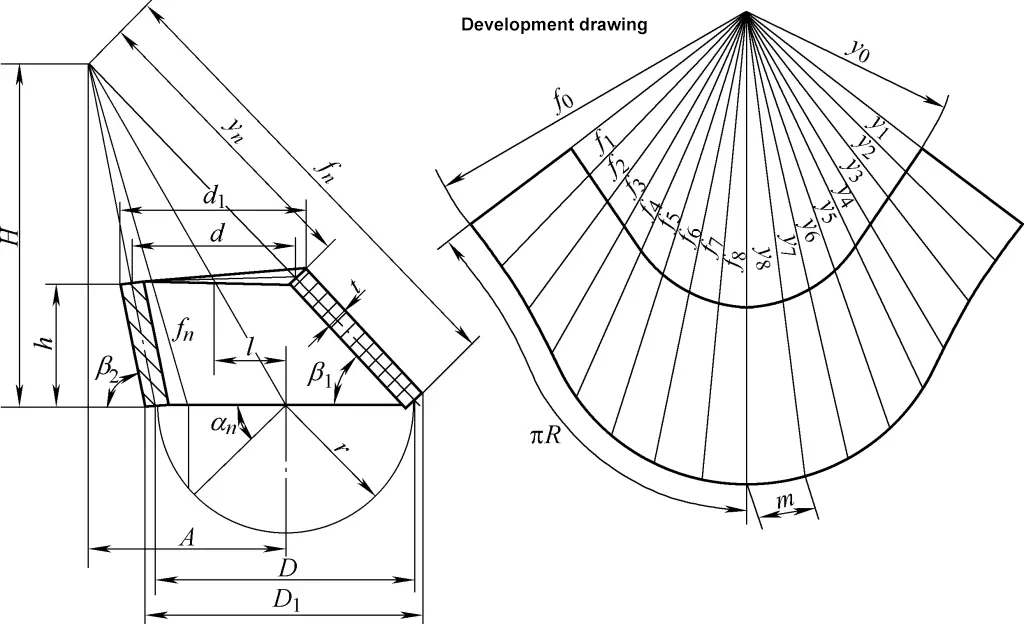
في الصيغة
- D1, d1 - الأقطار الخارجية للأطراف الكبيرة والصغيرة (مم);
- D، d - الأقطار المركزية للطرفين الكبير والصغير (مم);
- ح - الارتفاع المركزي (مم);
- ل - المسافة اللامتراكزة (مم);
- n - عدد الأقسام حول المحيط؛ كلما زاد عدد الأقسام، كلما كان عدد الأقسام أكبر، كلما كان الحساب أكثر تعقيدًا ولكن الرسم أكثر دقة. بشكل عام، يمكن الرجوع إلى عدد الأقسام في الجدول 1;
- fn, yn - أطوال الخطوط المائلة للمخروط الدائري القائم المائل (مم).
الجدول 1 عدد أقسام تطويرات الصفائح المعدنية
| نصف قطر القطعة المطورة/مم | عدد الأقسام |
| في حدود 50 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| أكثر من 2000 | 96 |
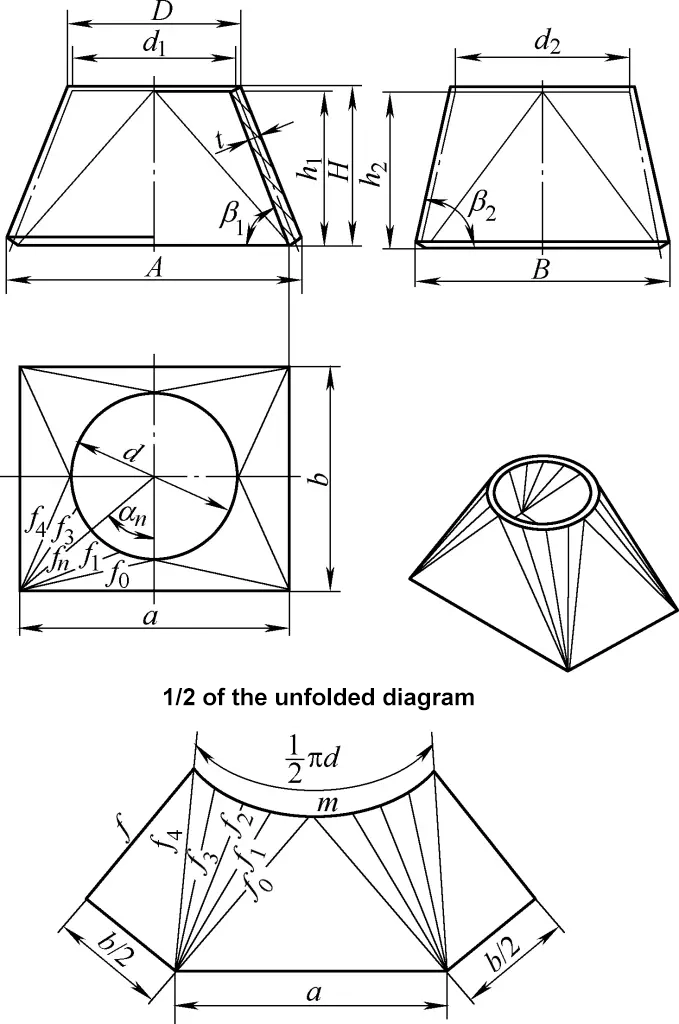
5. حساب تطوير القناة الانتقالية المستطيلة إلى الدائرية المستطيلة إلى الدائرية
تتكون القناة الانتقالية المستطيلة المتعامدة المستطيلة إلى الدائرية الموضحة في الشكل 5 من أربعة أسطح مخروطية دائرية قائمة مائلة متساوية وأربعة مستويات مثلثة متماثلة. الصيغة الحسابية لرسم تطورها هي:
تان1=2 ه/(أ-د)
تان2=2 ه/(ب-د)
d1= د-تسين بيتا1
d2= د-تسين بيتا2
د=1/2(د1+d2)= د-ت/2 (sinβ1+سين بيتا2)
أ=أ-2 تسين بيتا1
ب=ب-2 ت-2 تسن بيتا2
h1= هـ-ت/2 ج/ج/جوس1
h2= هـ-ت/2 ج/ج/جوس2
ح=1/2 (ح=1/2 (ح1+h2)= H-t/4 (جتا بيتا1+جوس بيتا2)
f0=1/2√[a2+(ب-د2)2+4h22]
fn=1/2√(أ-دسين ألفاn)2+(ب-دكوس ألفاn)2+4h2(عندما 0 <α<90 درجة مئوية)
fn=1/2√(أ-دسين ألفاn)2+(ب-دكوس ألفاn)2+4h12(عندما تكون α=90 درجة مئوية)
f=1/2√[(أ-د)2+4h12]
م= 𞸎/د/ن
لمعرفة معاني الرموز في الصيغة، راجع الشكل 5، و n هو عدد الأقسام حول المحيط. بشكل عام، يمكن أن يفي عدد الأقسام في الجدول 1 بمتطلبات الحساب.