Untuk komponen pembengkokan lembaran logam, menghitung ukuran kosong merupakan prasyarat untuk merumuskan rencana proses pembengkokan. Teknisi yang berbeda dapat memilih faktor kelonggaran tekukan yang berbeda dalam dokumen proses mereka, dan keakuratan ukuran blanko secara langsung berdampak pada keakuratan dimensi dan kualitas produk komponen tekukan.
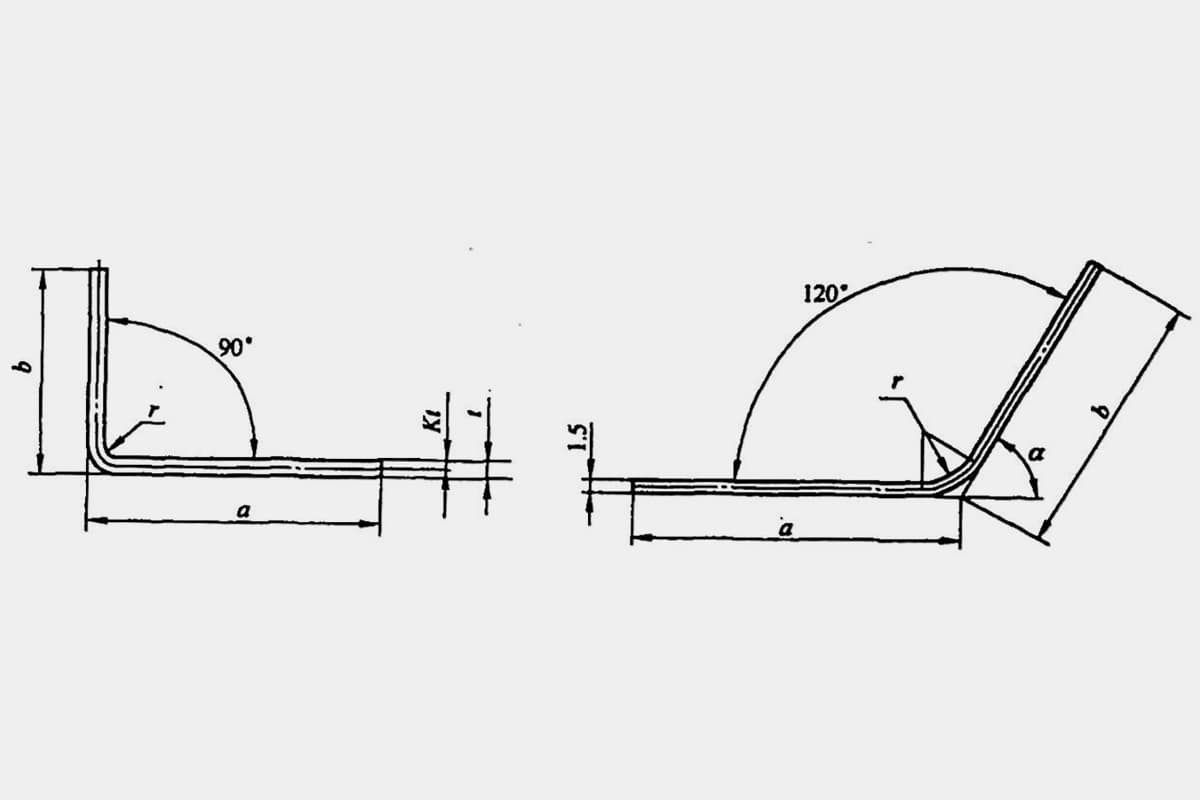
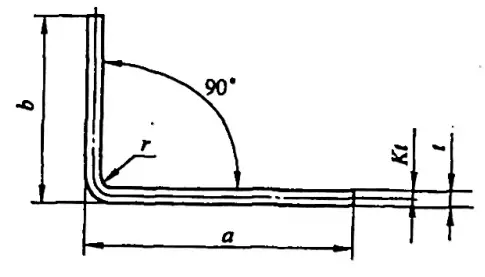
Terkadang, perhitungan yang tidak akurat bahkan dapat menghasilkan produk limbah. Panjang yang tidak dilipat L dari bagian tekukan sederhana yang khas (lihat Gambar 5-1) adalah L = a + b - y (di mana y adalah pengurangan tekukan, juga dikenal sebagai nilai koreksi untuk bagian R).
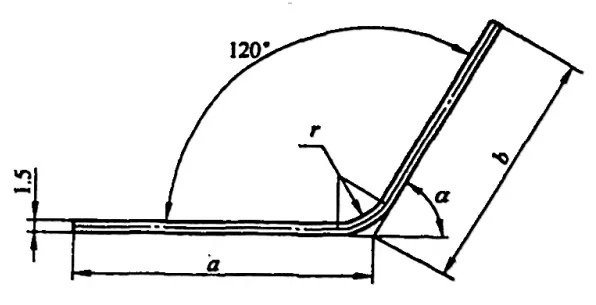
Namun, dalam berbagai manual dan material, pengurangan pembengkokan untuk φ = 90° dapat diperoleh secara langsung, sedangkan untuk pembengkokan non-90°, seperti yang ditunjukkan pada Gambar 5-2, teknisi perlu menghitungnya berdasarkan faktor pengalaman (faktor K).
Bacaan terkait: Seni Membentangkan Lembaran Logam Dijelaskan
1. Prinsip Menghitung Dimensi Tekukan Lembaran Logam yang Tidak Dilipat
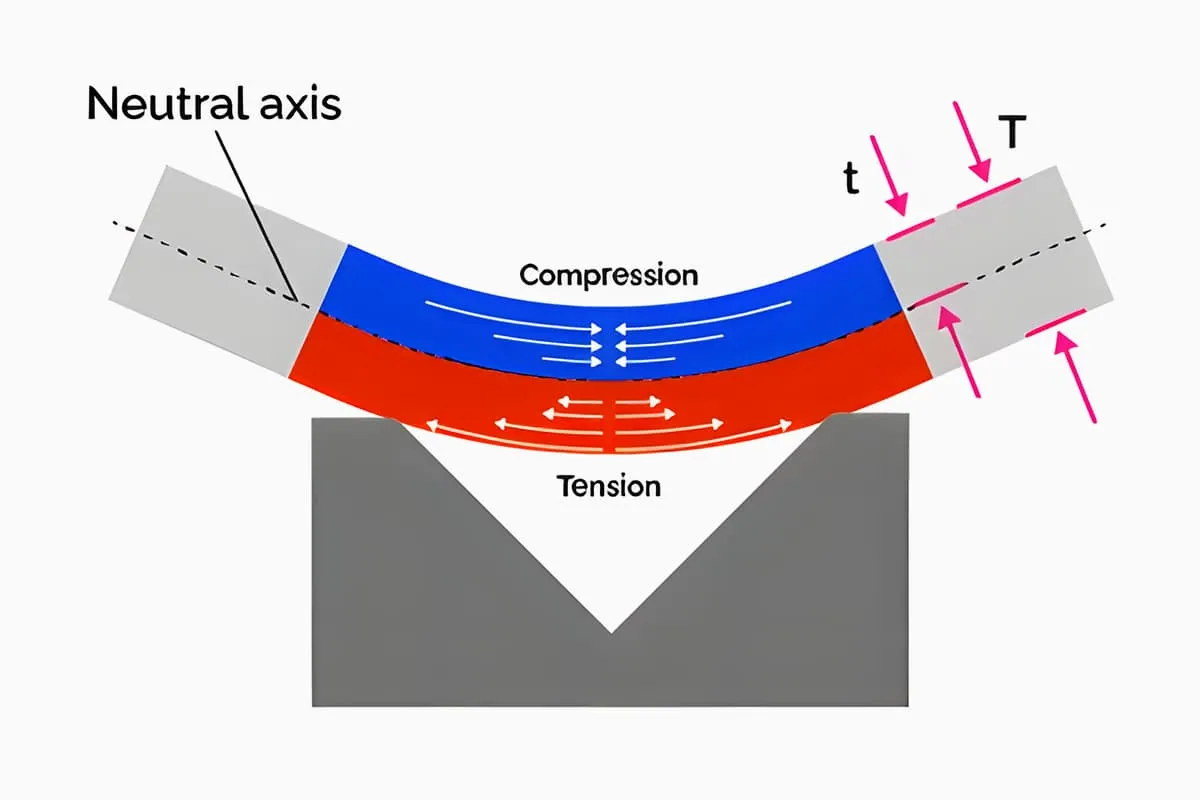
Dimensi yang tidak dilipat dari blanko yang ditekuk ditentukan berdasarkan prinsip bahwa panjang lapisan netral tetap tidak berubah sebelum dan sesudah ditekuk. Apabila lembaran logam ditekuk, serat lapisan luar bagian kosong diregangkan, dan serat lapisan dalam dikompresi.
Peregangan serat lapisan luar secara bertahap berkurang dari luar ke dalam, dan kompresi serat lapisan dalam juga secara bertahap berkurang dari dalam ke luar.
Ketika serat bertransisi dari peregangan ke kompresi atau dari kompresi ke peregangan, harus ada lapisan serat yang tegangan dan regangannya nol, dan panjangnya tetap tidak berubah sebelum dan sesudah ditekuk.
Lapisan inilah yang kita definisikan sebagai lapisan netral. Oleh karena itu, kunci untuk menghitung dimensi yang tidak dilipat dari blanko yang ditekuk adalah menentukan posisi lapisan netral. Posisi lapisan netral ditentukan berdasarkan kondisi volume bagian yang ditekuk dan blanko sama sebelum dan sesudah deformasi plastis.
2. Menentukan Jari-jari Kelengkungan ρ dari Lapisan Netral
Secara teori, karena deformasi yang tidak merata di sepanjang arah ketebalan bagian yang ditekuk, lapisan netral adalah permukaan parabola, tetapi demi perhitungan, biasanya dianggap sebagai permukaan busur melingkar. Ketika deformasi tekukan sangat kecil (r / t> 6,5), lapisan netral dapat dianggap berada di tengah-tengah ketebalan material, yaitu radius kelengkungan lapisan netral adalah ρ = r + t/2.
Apabila deformasi sangat besar (r/t≤6,5), ketebalan material akan menjadi lebih tipis, dan distorsi penampang menjadi sangat besar, seperti yang ditunjukkan pada Gambar 5-3.
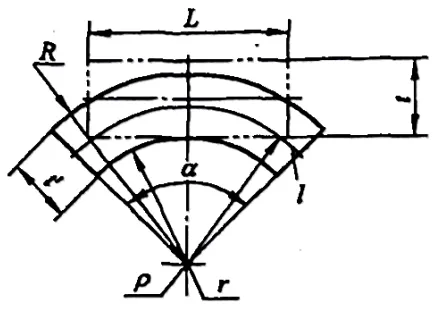
Pada saat ini, untuk memenuhi kondisi keseimbangan bahwa resultan gaya dari semua gaya yang bekerja pada bagian tersebut adalah nol, maka lapisan netral harus bergerak ke arah permukaan bagian dalam material.
Pada titik ini, kita dapat menentukan radius kelengkungan lapisan netral berdasarkan kondisi volume tidak berubah selama deformasi plastis, yaitu volume sebelum ditekuk: V0=LBt, dan volume setelah ditekuk:
V = (R2-r2)α*B'/2.
Dalam rumus, B adalah lebar blanko (mm); B' adalah lebar rata-rata blanko setelah ditekuk (mm); α adalah sudut pusat tekukan. Menurut prinsip bahwa volume sama sebelum dan sesudah pembengkokan, kita memiliki V0=V, yaitu,
LBt = (R2-r2)α*B'/2, dan L=(R2-r2)α*B'/2tB (5-1).
Dari tegangan dan regangan nol dari lapisan netral, kita mendapatkan L = l = αρ, di mana L adalah panjang sebelum deformasi lapisan netral (mm), dan l adalah panjang setelah deformasi lapisan netral (mm).
Dengan mengganti persamaan (5-1), kita mendapatkan ρ = (R2-r2)B'/2tB. Jika kita mengganti R = r + t' ke dalam persamaan di atas, kita bisa mendapatkan bentuk lain dari persamaan tersebut ρ = (r/t + η/2) tβη (5-2)dengan β adalah faktor lebar, β = B'/B, dan umumnya ketika pelat lebar (B>3t) ditekuk, biasanya dianggap bahwa β = 1; η adalah faktor penipisan, η = t'/t.
Persamaan (5-2) adalah rumus untuk menghitung posisi lapisan netral secara teoretis. Saat menghitung, kita harus mengetahui η, yaitu aturan penipisan. Nilai η dapat dirujuk pada Tabel 5-1.
Perlu diperhatikan bahwa aturan penipisan cukup kompleks, distribusi posisi lapisan netral di area pembengkokan tidak seragam, dan aturan penipisan juga terkait dengan banyak faktor seperti metode pembengkokan, lebar slot cetakan bawah pembengkokan, dan ketebalan material.
Hal ini menyebabkan kesalahan yang tidak dapat dihindari pada perhitungan teoretis posisi lapisan netral, sehingga mengurangi nilai aplikasi praktis metode penentuan teoretis.
Tabel 5-1: Faktor penipisan η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
Dalam produksi aktual, rumus empiris, yang lebih mudah daripada komputasi teoretis, biasanya digunakan untuk menentukan posisi sumbu netral, sebagai berikut:
ρ = r + Kt (5-3)
Dimana:
- ρ - Radius kelengkungan sumbu netral (mm)
- r - Jari-jari dalam pembengkokan bahan baku (mm)
- t - Ketebalan material (mm)
- K - Koefisien sumbu netral (empiris Faktor K), lihat Tabel 5-2
Tabel 5-2: Nilai empiris dari koefisien sumbu netral K
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
Catatan:
- K1 dapat digunakan untuk tikungan berbentuk V atau U dengan pelat atas atau pelat tekan.
- K2 cocok untuk tikungan berbentuk V tanpa pelat atas.
3. Perhitungan Dimensi Kosong yang Tidak Dilipat untuk Beberapa Tikungan Lembaran Logam Khas
Berdasarkan definisi lapisan netral, dimensi kosong yang tidak dilipat harus sama dengan panjang lapisan netral. Biasanya, berdasarkan pada bagian dalam radius tikungan r dari blanko, tikungan dikategorikan sebagai tikungan bersudut bundar dan tidak bersudut bundar: tikungan dianggap bersudut bundar apabila r>0,5t, dan tidak bersudut bundar apabila r<0,5t.
Selanjutnya, berdasarkan lebar pelat B, tikungan dikategorikan menjadi tikungan pelat lebar dan sempit: bila lebar pelat B>3t, maka disebut sebagai tikungan pelat lebar, dan bila lebar pelat B<3t, maka disebut sebagai tikungan pelat sempit.
Dalam praktik produksi, tikungan dengan radius sudut bundar (r>0,5t) dan pelat lebar (B>3t) adalah yang paling banyak digunakan, dan dengan mempertimbangkan universalitas tikungan, kami terutama membahas perhitungan dimensi kosong yang tidak dilipat untuk tikungan dengan radius sudut bundar dan pelat lebar selama penekukan.
3.1 Perhitungan Dimensi Kosong yang Tidak Dilipat untuk Tikungan Sudut Bulat (r>0,5t)
Ketika r>0,5t, B>3t, karena penipisan bagian tekukan tidak parah dan distorsi penampang kecil, panjang blanko dapat ditentukan berdasarkan prinsip bahwa panjang lapisan netral sama dengan dimensi blanko yang tidak dilipat.
Metode umum untuk menghitung dimensi kosong yang tidak dilipat dari tikungan sudut bundar (r>0,5t) dibagi menjadi: perhitungan koefisien tekukan dan perhitungan nilai pengurangan tekukan.
1. Perhitungan Koefisien Tekuk Tikungan Sudut Bulat (r>0.5t) untuk Dimensi Kosong yang Tidak Dilipat:
1) Koefisien tekukan adalah panjang bagian busur yang diukur di sepanjang lapisan netral zona deformasi tekukan (bagian R tekukan), seperti yang ditunjukkan pada Gambar 5-4.
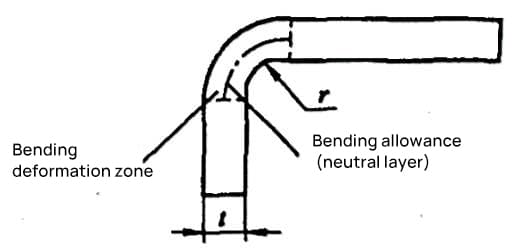
Koefisien tekukan dihitung dengan rumus (5-4): x = παρ / 180° (5-4)
Di mana ρ adalah jari-jari kelengkungan lapisan netral (mm).
2) Gambar 5-5 menunjukkan contoh notasi dimensi untuk perhitungan koefisien tekuk dimensi kosong yang tidak dilipat, dan rumusnya untuk menghitung koefisien tekuk dimensi kosong yang tidak dilipat adalah sebagai berikut.

a) φ> 90° b) φ≤90
L = a + b + x (5-5)
Dengan mengganti persamaan (5-3) ke dalam persamaan (5-4), kita mendapatkan rumus untuk koefisien tekukan:
x = πα (r + Kt) / 180° (5-6)
Dengan mengganti persamaan (5-6) ke dalam persamaan (5-5), kita memperoleh rumus untuk menghitung ukuran blanko yang tidak dilipat:
L = a + b + πα (r + Kt) / 180° (5-7)
Dimana:
- L - Ukuran blanko yang tidak dilipat (mm);
- K - Koefisien untuk faktor-K, lihat Tabel 5-2 untuk mengetahui nilainya;
- α - Sudut pusat pembengkokan, hubungannya dengan sudut bagian yang ditekuk adalah α = 180°-φ;
- r - Jari-jari tekukan lapisan dalam blanko (mm);
- t - Ketebalan bahan (mm);
- a, b - Panjang bagian lurus komponen (mm), masing-masing.
2. Perhitungan pengurangan tekukan untuk ukuran yang tidak dilipat dari bagian yang ditekuk pada sudut yang dibulatkan (r>0,5t)
1) Pengurangan tekukan (juga dikenal sebagai nilai koreksi untuk bagian R) adalah selisih antara dua kali R dari zona deformasi tekukan (bagian R dari tekukan) dan koefisien tekukan, seperti yang ditunjukkan pada Gambar 5-6.

Pengurangan pembengkokan (nilai koreksi untuk bagian R) dihitung sesuai persamaan (5-8):
y = 2R-παr / 180° (5-8)
2) Gambar 5-7 menunjukkan contoh anotasi dimensi untuk perhitungan pengurangan tekukan untuk ukuran blanko yang tidak dilipat. Pengurangan tekukan y dihitung dengan rumus berikut ini:
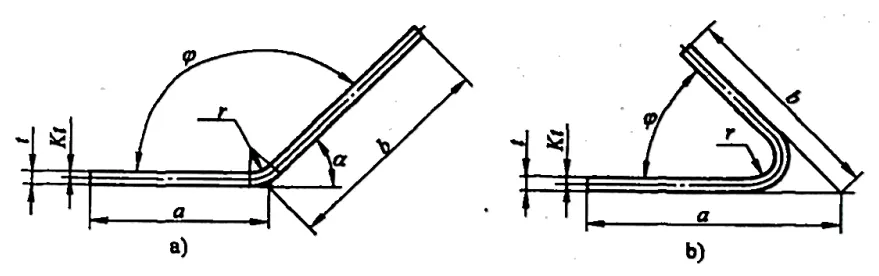
a)90° <φ≤165° b)φ≤90°
(1)Apabila φ ≤ 90°:
R = (r + t) / tan (φ/2)
Dengan mengganti rumus di atas dan rumus (5-3) ke dalam rumus (5-8), kita mendapatkan pengurangan pembengkokan (yaitu, nilai koreksi dari bagian R) untuk pembengkokan φ≤90° (lihat Gambar 5-7b):
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
②Ketika 90°<φ≤165°:
R=(r+t)tan[(180°-φ)/2]
Dengan mengganti rumus di atas dan rumus (5-3) ke dalam rumus (5-8), kita mendapatkan pengurangan pembengkokan (yaitu, nilai koreksi bagian R) untuk pembengkokan 90° <φ≤165° (lihat Gambar 5-7a):
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
③Ketika 165°<φ≤180°:
y≈0
3) Rumus untuk menghitung nilai pengurangan pembengkokan dari ukuran kosong bagian yang ditunjukkan pada Gambar 5-7 adalah:
L = a + b - y (5-11)
(1)Ketika φ≤90°, dengan mengganti rumus (5-9) ke dalam rumus (5-11), kita mendapatkan rumus untuk menghitung nilai pengurangan pembengkokan ukuran kosong sebagai berikut:
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
②Jika 90°<φ≤165°, dengan mengganti rumus (5-10) ke dalam rumus (5-11), kita mendapatkan rumus untuk menghitung nilai pengurangan tekukan ukuran kosong sebagai berikut:
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
③Ketika 165°<φ≤180°:
L≈a+b (5-14)
Dimana,
- y - Pengurangan pembengkokan (mm)
- L - Ukuran kosong bagian (mm)
- r - Jari-jari tekukan bagian dalam blanko (mm)
- t - Ketebalan material (mm)
- α - Sudut pusat tekukan, hubungannya dengan sudut tekukan adalah α = 180°-φ
- a, b-Panjang tepi bagian (mm) ke titik tekuk.
3. Perhitungan ukuran kosong untuk tikungan multi-sudut
Untuk tikungan multi-sudut, ukuran kosong adalah jumlah dari bagian R dan panjang tepi lurus.
1) Perhitungan ukuran blanko tikungan multi-sudut dengan koefisien tekukan:
L = l1+l2+...+ln+1+nx (5-15)
Di mana l1, l2...ln+1 adalah panjang bagian lurus dari setiap tepi bagian (mm);
n adalah jumlah tikungan R.
2) Perhitungan ukuran blanko tikungan multi-sudut dengan pengurangan tekukan:
L = l1+l2+...+ln+1-ny (5-16)
Di mana l1, l2...ln+1 adalah panjang tepi bagian (mm) ke titik tekuk;
n adalah jumlah tikungan R.
Contoh 5-1: Hitung ukuran kosong untuk tikungan yang ditunjukkan pada Gambar 5-8.
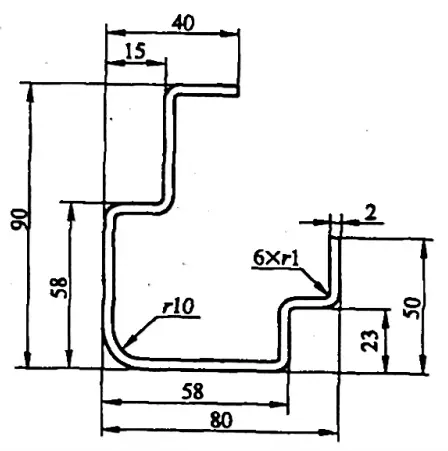
Solusi 1: Hitung ukuran blanko dengan menggunakan koefisien tekukan.
Lihat Lampiran A: Ketika sudut potongan lentur φ = 90°, ketebalan t = 2mm, dan jari-jari r = 10mm, koefisien lenturnya adalah 2,68mm;
Apabila sudut potongan lentur 90°, ketebalan t = 2mm, dan jari-jari r = 10mm, maka koefisien lenturnya adalah x2 = 16,9mm.
Dari persamaan (5-5) dan (5-15), ukuran datar blanko untuk bagian yang ditekuk dihitung sebagai:
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2,68 + 16,9] mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240,98mm.
Solusi 2: Hitung ukuran datar blanko dengan menggunakan nilai pengurangan tekukan.
Lihat Lampiran C: Untuk tikungan dengan sudut φ = 90°, ketebalan t = 2mm, dan jari-jari r = 1mm, nilai koreksi untuk bagian R adalah y1 = 3,32mm; untuk tikungan dengan sudut φ = 90°, ketebalan t = 2mm, dan jari-jari r = 10mm, nilai koreksi untuk bagian R adalah y2 = 7,1mm.
Ukuran baku bagian yang ditekuk dapat diperoleh dari persamaan (5-11) dan (5-16):
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3,32 - 7,1] mm
= (25+34+17+116+25+24+27-19,92-7,1) mm
= 240,98 mm
Contoh 5-2: Hitung ukuran mentah dari bagian yang ditekuk yang ditunjukkan pada Gambar 5-9.
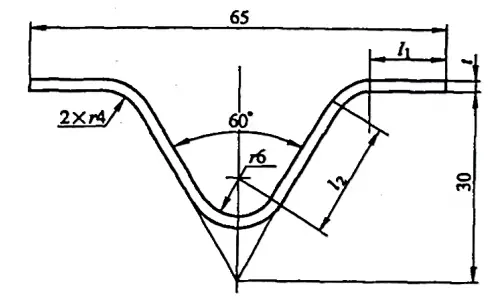
Solusi: Hitung ukuran baku dengan menggunakan koefisien pembengkokan.
Rumus untuk menghitung dimensi kosong dari bagian yang ditekuk dari persamaan (5-5) dan (5-15) adalah:
L = 2l1+2l2+2x1+x2
di mana l1 = [32,5 - (30tan30° + 4tan30°)] mm = 12,87 mm
dan l2 = [(30/cos30°) - (8/tan30° + 4tan30°)] mm = 18,47 mm
Merujuk Lampiran A: ketika sudut tekukan φ = 120°, t = 2mm, r = 4mm, nilai faktor tekukan adalah x1=4,98 mm; ketika sudut tekukan φ = 60 °, t = 2mm, r = 6mm, nilai faktor tekukan adalah x2=14.16mm.
Dengan mengganti nilai-nilai ini ke dalam rumus, akan menghasilkan panjang blanko yang tidak dilipat sebagai L= (2×12,87 + 2×18,47 + 2×4,98 + 14,16) mm = 86,8 mm.
Perlu dicatat bahwa untuk tikungan yang lebih sederhana dengan persyaratan presisi yang lebih rendah, dimensi blanko yang tidak dilipat dapat langsung dihitung. Namun demikian, untuk tikungan yang lebih rumit, atau yang memiliki persyaratan presisi yang lebih tinggi, bentuk dan dimensi blanko yang tidak dilipat perlu diuji berulang kali dan terus direvisi untuk mengonfirmasikan bentuk dan dimensi blanko.
3.2 Perhitungan Dimensi Pengembangan Kosong untuk Komponen Tikungan Tajam (r <0,5t)
Ketika radius tikungan r dari suatu komponen kurang dari 0,5t, maka komponen tersebut disebut sebagai tikungan tajam. Perhitungan dimensi pengembangan kosong untuk komponen tersebut didasarkan pada prinsip konsistensi volume sebelum dan sesudah pembengkokan.
Pada tikungan yang tajam, akibat penipisan material yang parah pada tikungan, proses deformasi menjadi sangat kompleks, sehingga sulit untuk menghitung dimensi pengembangan blank secara akurat. Oleh karena itu, dimensi pengembangan blank yang dihitung perlu dikoreksi berdasarkan data empiris atau melalui uji coba pembengkokan.
Rumus perhitungan untuk dimensi pengembangan blanko komponen tikungan tajam (r<0.5t, φ=90°) dapat ditemukan pada Tabel 5-3.
Tabel 5-3 Rumus perhitungan untuk dimensi pengembangan kosong dari komponen tikungan tajam (r <0,5t, φ = 90°) (satuan: mm)
| Nomor Seri | Fitur Pembengkokan | Skema | Formula |
| 1 | Membelok di tikungan. |  | L = a + b + 0,4t |
| 2 | Ratakan. |  | L = a + b - 0,43t |
| 3 | Tekuk dua sudut sekaligus. | 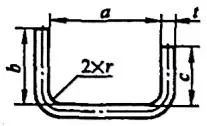 | L = a + b + c + 0,6t |
| 4 | Tekuk tiga sudut secara bersamaan. | 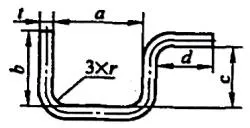 | L = a + b + c + d + 0,75t |
| 5 | Tekuk dua sudut pada contoh pertama, dan tekuk sudut lainnya pada contoh kedua. | L = a + b + c + d + t | |
| 6 | Tekuk empat sudut secara bersamaan. | 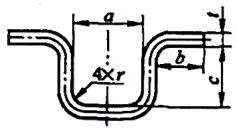 | L = a + 2b + 2c + 1.2t |
| 7 | Tekuk untuk membentuk empat sudut dalam dua contoh. | L = a + 2b + 2c + 1.2t |
3.3 Perhitungan Dimensi yang Tidak Dilipat untuk Komponen Tekuk Tipe Engsel
Untuk tipe engsel bagian yang bengkok dengan r = (0,6 ~ 3,5) t (lihat Gambar 5-10), proses flensing biasanya mengikuti pola yang ditunjukkan pada Gambar 5-11. Selama proses flensing, ketebalan lembaran logam bertambah dan lapisan netral bergeser ke luar. Dimensi blanko yang tidak dilipat dapat dihitung secara perkiraan dengan rumus berikut:
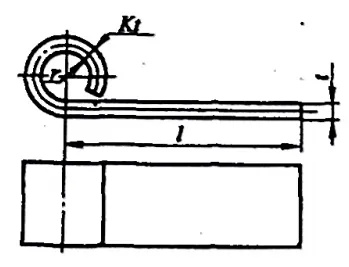
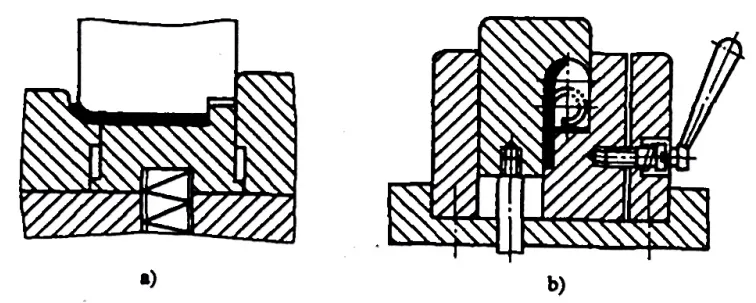
- a) Operasi pertama
- b) Operasi kedua
L = l + 1,57π (r + Kt) + r
Dimana:
- L - Dimensi blanko yang tidak dilipat (mm);
- l - Panjang segmen lurus (mm);
- r - Jari-jari tekukan internal blanko (mm);
- K - Koefisien perpindahan lapisan netral. Apabila r/t = 0,5 ~ 1,8, K biasanya diambil sebagai 0,5 ~ 0,70 (semakin kecil nilai r/t, semakin besar nilai K; sebaliknya, semakin kecil nilai K). Ini juga dapat dipilih menurut Tabel 5-4.
Tabel 5-4 Koefisien Perpindahan Lapisan Netral untuk Komponen Lentur Tipe Engsel
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |