Durante il processo di creazione del disegno di sviluppo del componente in lamiera, è necessario considerare anche l'impatto dello spessore del materiale di lavorazione, ovvero effettuare le opportune regolazioni dello spessore della lamiera.
In generale, per le lamiere di spessore inferiore a 3 mm, non è necessaria alcuna regolazione dello spessore della piastra. Può essere calcolato in base al diametro centrale della lamiera o in base alle linee di taglio della superficie interna ed esterna. Le dimensioni dopo la formatura rientrano nell'intervallo di deviazione consentito. Quando lo spessore della lamiera è superiore a 3 mm, deve essere calcolato in base al diametro centrale della lamiera. Per comodità di descrizione, i calcoli per i seguenti materiali sviluppati si riferiscono al diametro centrale della lamiera.
1. Calcolo dello sviluppo di gusci cilindrici
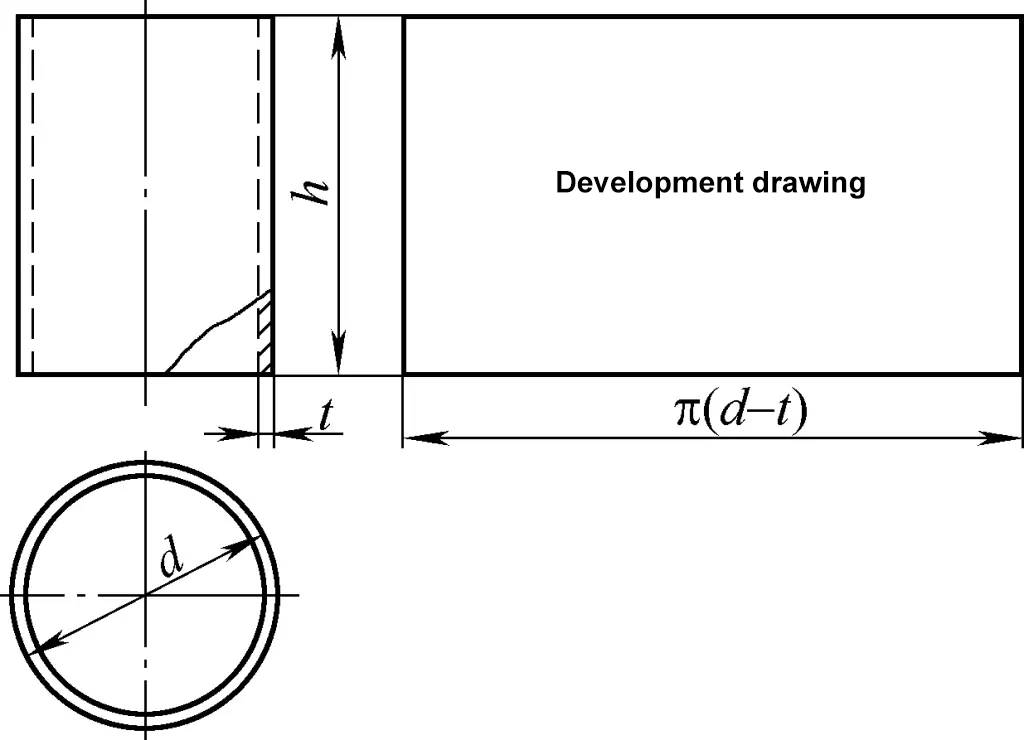
Il guscio cilindrico appartiene alla superficie cilindrica e il suo disegno di sviluppo è un rettangolo. Un lato del rettangolo è uguale alla circonferenza del cilindro π(d-t) e l'altro lato è l'altezza h del cilindro, come mostrato nella Figura 1. Nella figura, d è il diametro esterno del cilindro e t è lo spessore della piastra. Nella figura, d è il diametro esterno del cilindro e t è lo spessore della piastra.
2. Calcolo dello sviluppo di coni circolari retti
Il disegno di sviluppo del cono circolare destro è un arco di settore. La formula di calcolo per il disegno di sviluppo del cono circolare destro mostrato nella Figura 2 è:
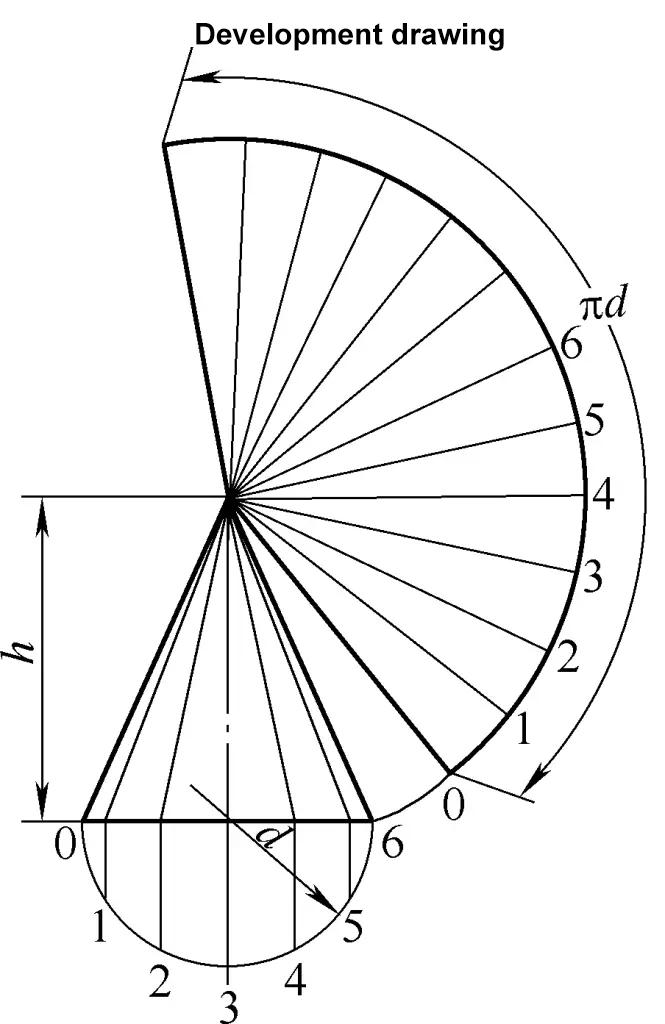
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
Nella formula
- R - Raggio dell'arco di settore (mm);
- α - Angolo del settore (°);
- L - Lunghezza della corda dell'arco di settore (mm).
3. Calcolo dello sviluppo di coni circolari destri troncati
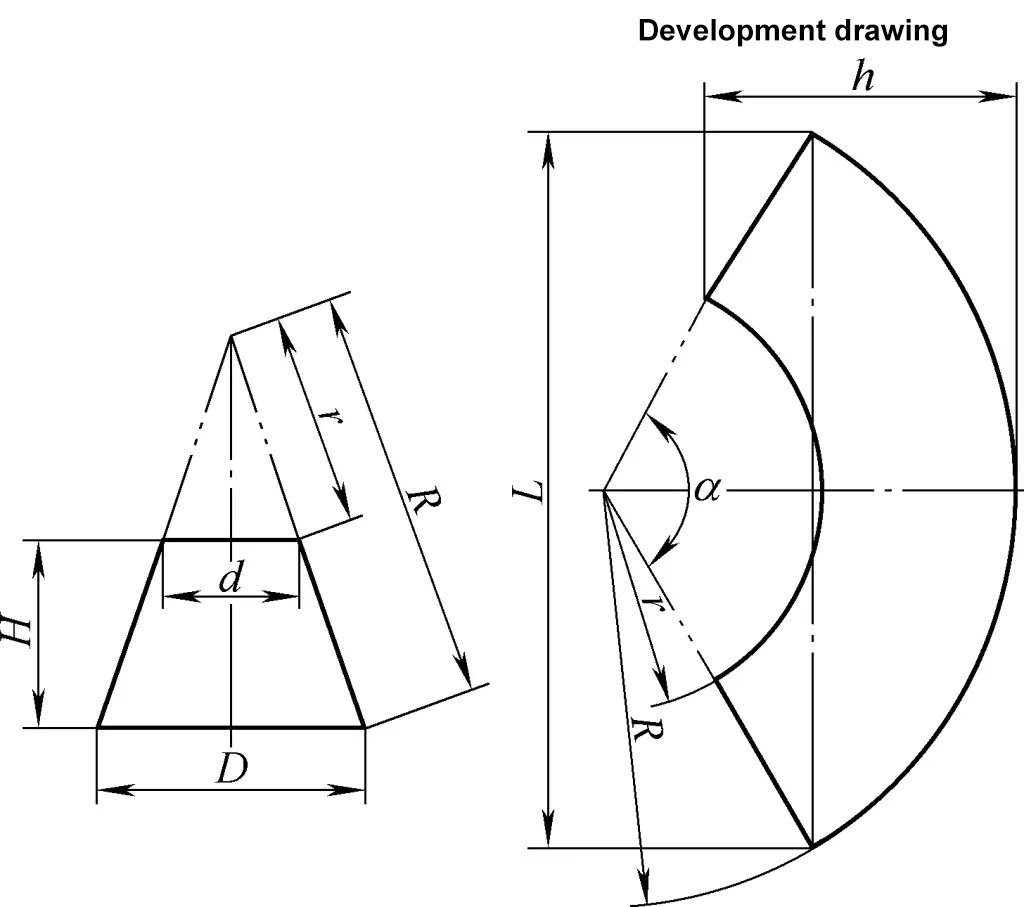
Il disegno di sviluppo del tronco di cono circolare destro è un arco di settore concentrico. La formula di calcolo per il disegno di sviluppo del tronco di cono circolare destro mostrato nella Figura 3 è:
R=√{(D/2)2+[DH/(D-d)]2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
Quando α>180°, h=R+rsin[(α-180)/2]
Per il significato dei simboli della formula, fare riferimento alla Figura 3.
4. Calcolo dello sviluppo di coni circolari retti obliqui
Il disegno di sviluppo del cono circolare destro obliquo è un arco di settore irregolare. La formula di calcolo per il disegno di sviluppo del cono circolare obliquo destro mostrato nella Figura 4 è:
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[(A-D/2cosαn)2+(D/2)2peccato2αn+H2]
yn=fn(1-h/H)
m=Dsin(180°/n )
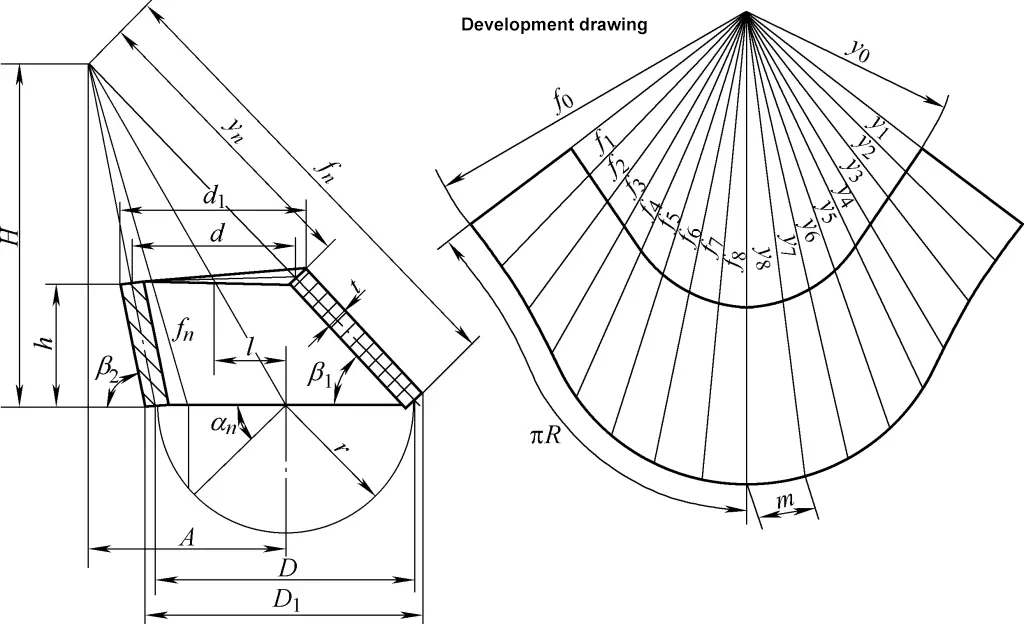
Nella formula
- D1, d1 - Diametri esterni delle estremità grandi e piccole (mm);
- D, d - Diametri centrali delle estremità grandi e piccole (mm);
- h - Altezza centrale (mm);
- l - Distanza eccentrica (mm);
- n - Numero di divisioni intorno alla circonferenza; più alto è il numero di divisioni, più complesso è il calcolo ma più accurato è il disegno. In generale, il numero di divisioni può essere indicato nella Tabella 1;
- fn, yn - Lunghezze delle linee oblique del cono circolare destro obliquo (mm).
Tabella 1 Numero di divisioni per lo sviluppo della lamiera
| Raggio del pezzo sviluppato/mm | Numero di divisioni |
| Entro il 50 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| Oltre 2000 | 96 |
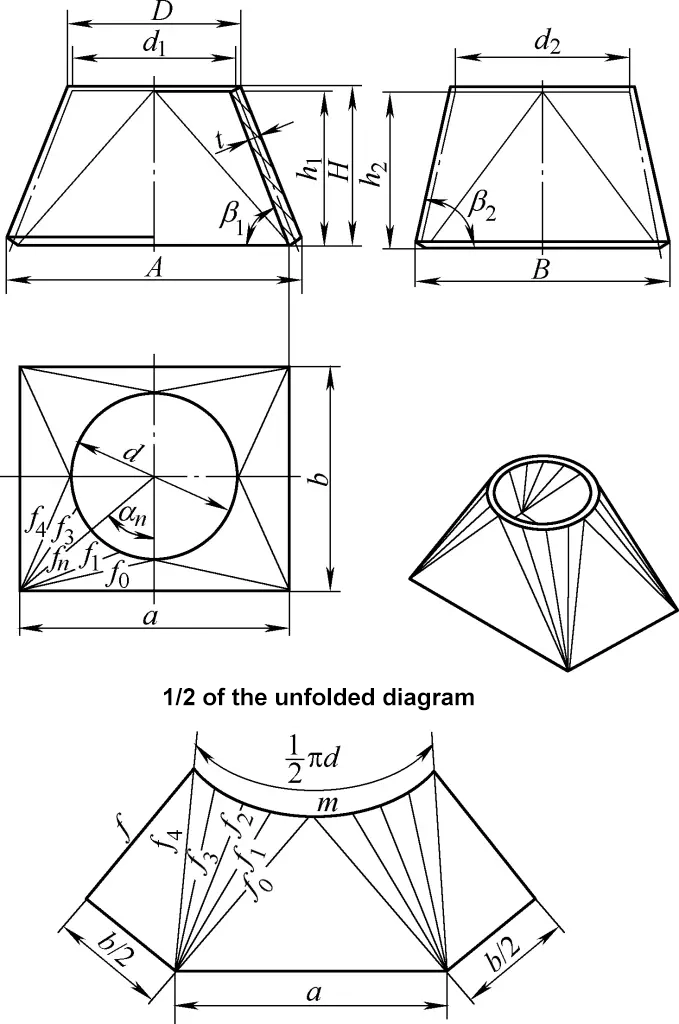
5. Calcolo dello sviluppo del condotto di transizione ortogonale da rettangolare a rotondo
Il condotto di transizione ortoconico da rettangolare a rotondo mostrato nella Figura 5 è costituito da quattro superfici coniche circolari destre oblique uguali e da quattro piani triangolari simmetrici. La formula di calcolo per il suo disegno di sviluppo è:
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(quando 0<α<90°)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(quando α=90°)
f=1/2√[(a-d)2+4h12]
m=πd/n
Per il significato dei simboli della formula, fare riferimento alla Figura 5, mentre n è il numero di divisioni intorno alla circonferenza. In generale, il numero di divisioni della Tabella 1 può soddisfare i requisiti di calcolo.