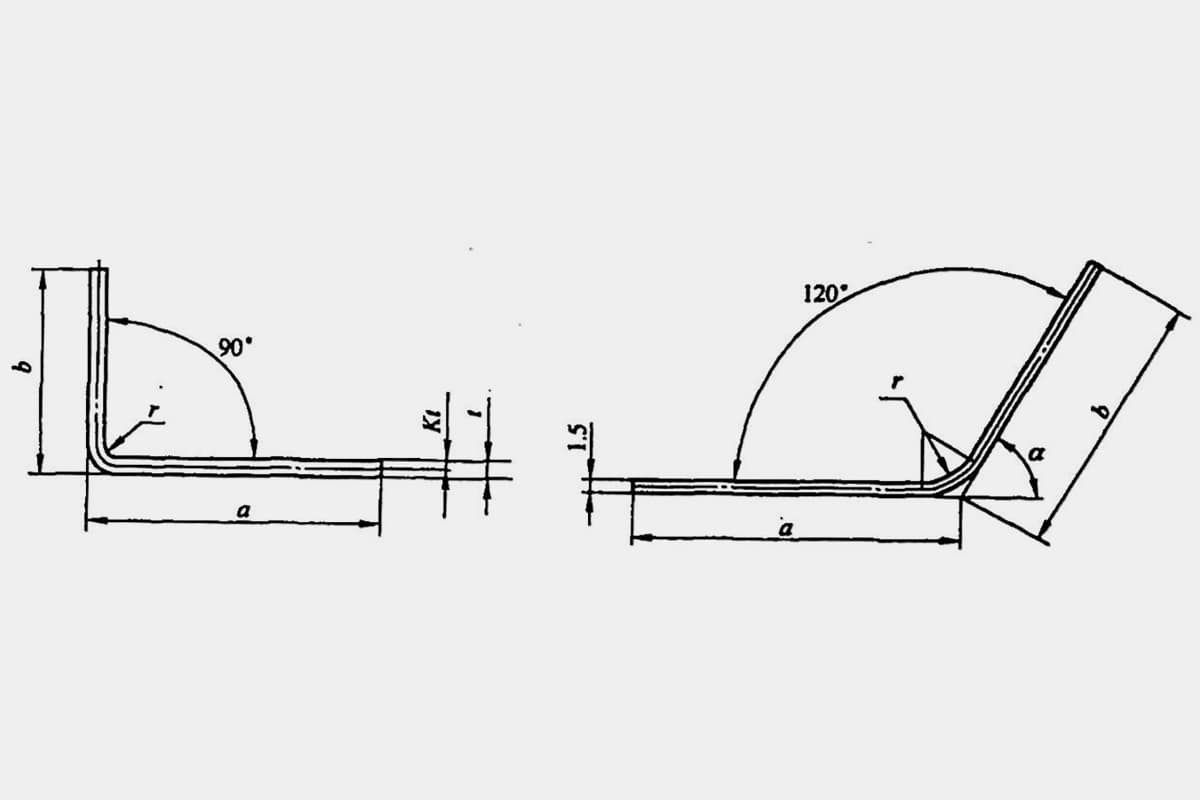
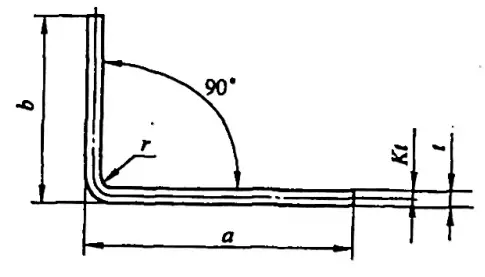
Per i pezzi di piegatura della lamiera, il calcolo delle dimensioni dello spezzone è un prerequisito per la formulazione del piano del processo di piegatura. Tecnici diversi possono selezionare fattori di tolleranza di piegatura diversi nei loro documenti di processo e l'accuratezza delle dimensioni dello spezzone influisce direttamente sulla precisione dimensionale e sulla qualità del prodotto dei pezzi di piegatura.
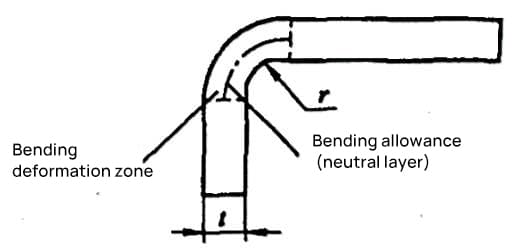
A volte, calcoli imprecisi possono addirittura dare origine a prodotti di scarto. La lunghezza dispiegata L di un tipico pezzo a flessione semplice (vedi Figura 5-1) è L = a + b - y (dove y è la deduzione di flessione, nota anche come valore di correzione per il pezzo R).
Tuttavia, in vari manuali e materiali, la deduzione di flessione per φ=90° può essere ottenuta direttamente, mentre per le curve non a 90°, come quelle mostrate nella Figura 5-2, i tecnici devono calcolarla in base a un fattore di esperienza (fattore K).
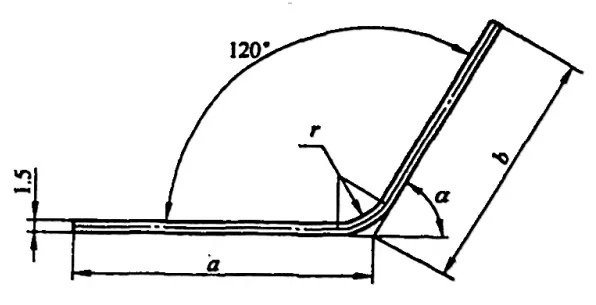
Lettura correlata: L'arte della piegatura delle lamiere spiegata
1. Principio di calcolo della dimensione non piegata delle curve di lamiera
La dimensione non piegata di un pezzo grezzo piegato è determinata in base al principio che la lunghezza dello strato neutro rimane invariata prima e dopo la piegatura. Quando la lamiera viene piegata, le fibre dello strato esterno della sezione del grezzo si allungano e le fibre dello strato interno si comprimono.
L'allungamento delle fibre dello strato esterno diminuisce gradualmente dall'esterno verso l'interno e anche la compressione delle fibre dello strato interno diminuisce gradualmente dall'interno verso l'esterno.
Quando le fibre passano dall'allungamento alla compressione o dalla compressione all'allungamento, deve esistere uno strato di fibre in cui le sollecitazioni e le deformazioni sono nulle e la cui lunghezza rimane invariata prima e dopo la flessione.
Questo strato è quello che definiamo strato neutro. Pertanto, la chiave per calcolare la dimensione non piegata del pezzo piegato è determinare la posizione dello strato neutro. La posizione dello strato neutro viene determinata in base alla condizione che il volume della parte piegata e del pezzo grezzo siano uguali prima e dopo la deformazione plastica.
2. Determinazione del raggio di curvatura ρ dello strato neutro
In teoria, a causa della deformazione non uniforme lungo la direzione dello spessore della parte piegata, lo strato neutro è una superficie parabolica, ma per motivi di calcolo viene solitamente considerato come una superficie ad arco di cerchio. Quando la deformazione di flessione è molto piccola (r/t >6,5), lo strato neutro può essere approssimativamente considerato a metà dello spessore del materiale, cioè il raggio di curvatura dello strato neutro è ρ=r+t/2.
Quando la deformazione è molto grande (r/t≤6,5), lo spessore del materiale si assottiglia e la distorsione della sezione è molto grande, come mostrato nella Figura 5-3.
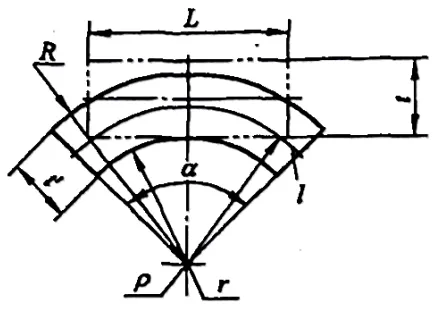
A questo punto, per soddisfare la condizione di equilibrio secondo cui la risultante di tutte le forze agenti nella sezione è pari a zero, lo strato neutro deve spostarsi verso la superficie interna del materiale.
A questo punto, possiamo determinare il raggio di curvatura dello strato neutro in base alla condizione che il volume non cambi durante la deformazione plastica, cioè il volume prima della flessione: V0=LBt, e il volume dopo la piegatura:
V=(R2-r2)α*B'/2.
Nella formula, B è la larghezza del grezzo (mm); B' è la larghezza media del grezzo dopo la piegatura (mm); α è l'angolo centrale di piegatura. Secondo il principio che il volume è uguale prima e dopo la piegatura, si ha V0=V, cioè,
LBt=(R2-r2)α*B'/2, e L=(R2-r2)α*B'/2tB (5-1).
Dalle tensioni e dalle deformazioni nulle dello strato neutro, si ottiene L=l=αρ, dove L è la lunghezza prima della deformazione dello strato neutro (mm) e l è la lunghezza dopo la deformazione dello strato neutro (mm).
Sostituendo l'equazione (5-1), si ottiene ρ=(R2-r2)B'/2tB. Se sostituiamo R=r+t' all'equazione precedente, possiamo ottenere un'altra forma di equazione ρ=(r/t+η/2)tβη (5-2), dove β è il fattore di larghezza, β=B'/B, e in genere quando una lastra larga (B>3t) viene piegata, si considera che β=1; η è il fattore di assottigliamento, η=t'/t.
L'equazione (5-2) è la formula per calcolare teoricamente la posizione dello strato neutro. Per il calcolo è necessario conoscere η, ovvero la regola di assottigliamento. Il valore di η è riportato nella Tabella 5-1.
Va sottolineato che la regola dell'assottigliamento è piuttosto complessa, la distribuzione della posizione dello strato neutro nell'area di piegatura non è uniforme e la regola dell'assottigliamento è anche legata a molti fattori, come il metodo di piegatura, la larghezza della fessura inferiore dello stampo di piegatura e lo spessore del materiale.
Ciò comporta inevitabili errori nel calcolo teorico della posizione dello strato neutro, riducendo così il valore di applicazione pratica del metodo di determinazione teorica.
Tabella 5-1: Fattore di assottigliamento η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
Nella produzione reale, per determinare la posizione dell'asse neutro si utilizza in genere una formula empirica, più semplice del calcolo teorico, come segue:
ρ = r + Kt (5-3)
Dove:
- ρ - Raggio di curvatura dell'asse neutro (mm)
- r - Raggio interno di curvatura della materia prima (mm)
- t - Spessore del materiale (mm)
- K - Coefficiente dell'asse neutro (empirico) Fattore K), fare riferimento alla Tabella 5-2
Tabella 5-2: Valori empirici del coefficiente dell'asse neutro K
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
Nota:
- K1 è applicabile alle curve a V o a U con piastra superiore o piastra di pressatura.
- K2 è adatto alle curve a V senza piastra superiore.
3. Calcolo delle dimensioni del vuoto non piegato per diverse curve tipiche della lamiera
In base alla definizione di strato neutro, la dimensione del fustellato dispiegato deve essere pari alla lunghezza dello strato neutro. In genere, in base alla dimensione interna raggio di curvatura r del pezzo grezzo, le curve sono classificate come curve ad angolo tondo e non ad angolo tondo: le curve sono considerate ad angolo tondo quando r>0,5t, e non ad angolo tondo quando r<0,5t.
Inoltre, in base alla larghezza della piastra B, le curve vengono classificate in curve a piastra larga e stretta: quando la larghezza della piastra B>3t, si parla di curva a piastra larga, mentre quando la larghezza della piastra B<3t, si parla di curva a piastra stretta.
Nella pratica produttiva, le curve con raggio ad angolo tondo (r>0,5t) e le lamiere larghe (B>3t) sono le più utilizzate e, considerando l'universalità delle curve, discutiamo principalmente il calcolo delle dimensioni del grezzo non piegato per le curve con raggio ad angolo tondo e le lamiere larghe durante la piegatura.
3.1 Calcolo delle dimensioni del vuoto non piegato per curve ad angolo tondo (r>0,5t)
Quando r>0,5t, B>3t, a causa dell'assottigliamento della parte in flessione non è grave e la distorsione della sezione trasversale è piccola, la lunghezza del grezzo può essere determinata in base al principio che la lunghezza dello strato neutro è uguale alla dimensione del grezzo non piegato.
I metodi comuni per il calcolo delle dimensioni del grezzo non piegato delle curve ad angolo tondo (r>0,5t) si dividono in: calcolo del coefficiente di flessione e calcolo del valore di deduzione della flessione.
1. Calcolo del coefficiente di flessione per le dimensioni del vuoto non piegato:
1) Il coefficiente di flessione è la lunghezza della parte di arco misurata lungo lo strato neutro della zona di deformazione da flessione (parte R di flessione), come illustrato nella Figura 5-4.
Il coefficiente di flessione è calcolato con la formula (5-4): x=παρ/180° (5-4)
Dove ρ è il raggio di curvatura dello strato neutro (mm).
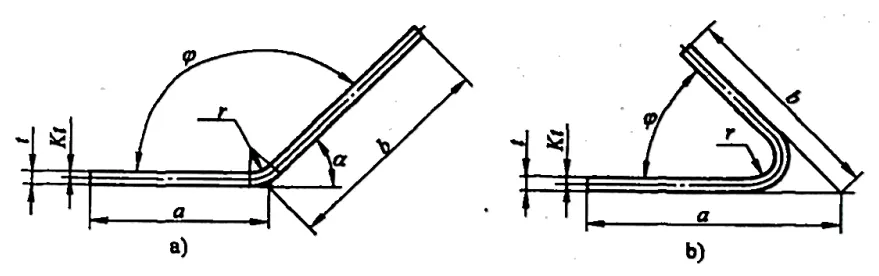
2) La Figura 5-5 mostra un esempio di notazione dimensionale per il calcolo del coefficiente di flessione delle dimensioni del grezzo non piegato e la formula per il calcolo del coefficiente di flessione delle dimensioni del grezzo non piegato è la seguente.

a) φ > 90° b) φ≤90
L=a+b+x (5-5)
Sostituendo l'equazione (5-3) nell'equazione (5-4), si ottiene la formula del coefficiente di flessione:
x=πα(r+Kt)/180° (5-6)
Sostituendo l'equazione (5-6) nell'equazione (5-5), si ottiene la formula per il calcolo delle dimensioni del fustellato piegato:
L=a+b+πα(r+Kt)/180° (5-7)
Dove:
- L - La dimensione del fustellato non piegato (mm);
- K - Coefficiente per il fattore K, fare riferimento alla Tabella 5-2 per il suo valore;
- α - L'angolo centrale di flessione, il suo rapporto con l'angolo della parte piegata è α=180°-φ;
- r - Raggio di curvatura dello strato interno del pezzo grezzo (mm);
- t - Lo spessore del materiale (mm);
- a, b - Le lunghezze delle parti diritte del componente (mm), rispettivamente.
2. Calcolo della deduzione di flessione per la dimensione non piegata di una parte piegata ad angolo arrotondato (r>0,5t)
1) La deduzione di flessione (nota anche come valore di correzione per la parte R) è la differenza tra il doppio di R della zona di deformazione di flessione (la parte R della flessione) e il coefficiente di flessione, come mostrato nella Figura 5-6.

La deduzione di flessione (valore di correzione per la parte R) viene calcolata secondo l'equazione (5-8):
y = 2R-παr/180° (5-8)
2) La Figura 5-7 mostra un esempio di annotazione delle dimensioni per il calcolo della deduzione di flessione per la dimensione non piegata del pezzo grezzo. La deduzione di flessione y viene calcolata con la seguente formula:
a)90°<φ≤165° b)φ≤90°
Quando φ ≤ 90°:
R=(r+t)/tan(φ/2)
Sostituendo la formula precedente e la formula (5-3) nella formula (5-8), si ottiene la deduzione di curvatura (cioè il valore di correzione della parte R) per una curvatura φ≤90° (vedere Figura 5-7b):
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
②Quando 90°<φ≤165°:
R=(r+t)tan[(180°-φ)/2]
Sostituendo la formula precedente e la formula (5-3) nella formula (5-8), si ottiene la deduzione di curvatura (cioè il valore di correzione della parte R) per una curvatura di 90°<φ≤165° (vedere Figura 5-7a):
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
③Quando 165°<φ≤180°:
y≈0
3) La formula per calcolare il valore della deduzione di flessione della dimensione del pezzo grezzo mostrato nella Figura 5-7 è la seguente:
L=a+b-y (5-11)
①Quando φ≤90°, sostituendo la formula (5-9) nella formula (5-11), si ottiene la formula per il calcolo del valore della deduzione di flessione della dimensione dello spezzone come segue:
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
②Quando 90°<φ≤165°, sostituendo la formula (5-10) nella formula (5-11), si ottiene la formula per il calcolo del valore della deduzione di flessione della dimensione dello spezzone come segue:
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
③Quando 165°<φ≤180°:
L≈a+b (5-14)
Dove,
- y - Deduzione di flessione (mm)
- L - Dimensione del pezzo in bianco (mm)
- r - Raggio interno di curvatura del pezzo grezzo (mm)
- t - Spessore del materiale (mm)
- α - Angolo del centro di curvatura, la sua relazione con l'angolo di curvatura è α=180°-φ
- a, b-Lunghezze degli spigoli del pezzo (mm) rispetto al vertice di flessione.
3. Calcolo delle dimensioni dello spezzone per le curve multiangolo
Per le curve multiangolo, la dimensione dello spezzone è data dalla somma della parte R e delle lunghezze dei bordi rettilinei.
1) Calcolo delle dimensioni del pezzo grezzo a piegatura multiangolare in base al coefficiente di piegatura:
L=l1+l2+...+ln+1+nx (5-15)
Dove l1, l2...ln+1 sono le lunghezze delle parti rettilinee di ciascun bordo del pezzo (mm);
n è il numero di curve R.
2) Calcolo delle dimensioni del grezzo di piegatura multiangolare mediante la deduzione di piegatura:
L=l1+l2+...+ln+1-ny (5-16)
Dove l1, l2...ln+1 sono le lunghezze dei bordi del pezzo (mm) rispetto al vertice di flessione;
n è il numero di curve R.
Esempio 5-1: Calcolare le dimensioni dello spezzone per la curva illustrata nella Figura 5-8.
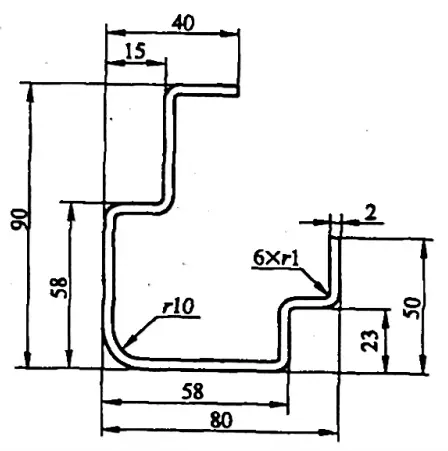
Soluzione 1: calcolare la dimensione dello spezzone utilizzando il coefficiente di flessione.
Fare riferimento all'Appendice A: quando l'angolo di piegatura del pezzo φ=90°, lo spessore t=2 mm e il raggio r=10 mm, il coefficiente di piegatura è di 2,68 mm;
Quando l'angolo di curvatura è di 90°, lo spessore t=2mm e il raggio r=10mm, il coefficiente di curvatura è x2=16,9mm.
Dalle equazioni (5-5) e (5-15), la dimensione piana del pezzo grezzo per il pezzo piegato è calcolata come:
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2,68 + 16,9]mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240,98 mm.
Soluzione 2: calcolare la dimensione piana del pezzo grezzo utilizzando il valore della deduzione di piegatura.
Fare riferimento all'Appendice C: per una curva con angolo φ=90°, spessore t=2mm e raggio r=1mm, il valore di correzione per la sezione R è y1=3,32mm; per una curva con angolo φ=90°, spessore t=2mm e raggio r=10mm, il valore di correzione per la sezione R è y2=7,1mm.
La dimensione grezza della parte piegata può essere ottenuta dalle equazioni (5-11) e (5-16):
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3.32 - 7.1] mm
= (25+34+17+116+25+24+27-19,92-7,1) mm
= 240,98 mm
Esempio 5-2: Calcolo della dimensione grezza del pezzo piegato mostrato nella Figura 5-9.
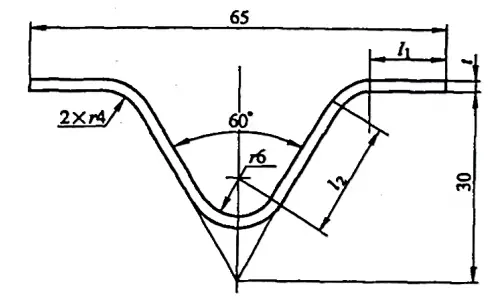
Soluzione: Calcolare la dimensione grezza utilizzando il coefficiente di flessione.
La formula per calcolare le dimensioni dello spezzone del pezzo piegato dalle equazioni (5-5) e (5-15) è la seguente:
L=2l1+2l2+2x1+x2
dove l1 = [32,5 - (30tan30°+4tan30°)] mm = 12,87 mm
e l2 = [(30/cos30°) - (8/tan30°+4tan30°)] mm = 18,47 mm
Facendo riferimento all'Appendice A: quando l'angolo di curvatura φ=120°, t=2mm, r=4mm, il valore del fattore di curvatura è x1=4,98 mm; quando l'angolo di curvatura φ=60°, t=2 mm, r=6 mm, il valore del fattore di curvatura è x2=14,16 mm.
Sostituendo questi valori nella formula, la lunghezza dello spezzone aperto risulta L= (2×12,87 + 2×18,47 + 2×4,98 + 14,16) mm = 86,8 mm.
Va notato che per le curve più semplici con requisiti di precisione inferiori, le dimensioni dello spezzone non piegato possono essere calcolate direttamente. Tuttavia, per curve più complesse o con requisiti di precisione più elevati, la forma e le dimensioni dello spezzone non piegato devono essere ripetutamente testate e continuamente riviste per confermare la forma e le dimensioni dello spezzone.
3.2 Calcolo delle dimensioni di sviluppo del grezzo per i componenti a curva stretta (r<0,5t)
Quando il raggio di curvatura r di un componente è inferiore a 0,5t, si parla di curva a gomito. Il calcolo della dimensione di sviluppo del pezzo grezzo per questi componenti si basa sul principio della consistenza del volume prima e dopo la piegatura.
Nelle curve strette, a causa del forte assottigliamento del materiale in corrispondenza della curva, il processo di deformazione è estremamente complesso e rende difficile il calcolo accurato delle dimensioni di sviluppo dello spezzone. Pertanto, le dimensioni di sviluppo dello spezzone calcolate devono essere corrette sulla base di dati empirici o mediante piegature di prova.
La formula di calcolo per le dimensioni di sviluppo dello spezzone di componenti a curva acuta (r<0,5t, φ=90°) è riportata nella Tabella 5-3.
Tabella 5-3 Formula di calcolo per le dimensioni di sviluppo dello spezzone di componenti a curva acuta (r<0,5t, φ=90°) (unità: mm)
| Numero di serie | Caratteristiche di piegatura | Schema | Formula |
| 1 | Piegare un angolo. |  | L=a+b+0,4t |
| 2 | Appiattirlo. |  | L=a+b-0,43t |
| 3 | Piegare due angoli contemporaneamente. | 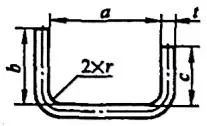 | L=a+b+c+0,6t |
| 4 | Piegare tre angoli contemporaneamente. | 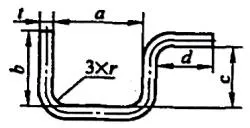 | L=a+b+c+d+0,75t |
| 5 | Piegare due angoli nel primo caso e piegare un altro angolo nel secondo. | L=a+b+c+d+t | |
| 6 | Piegare quattro angoli contemporaneamente. | 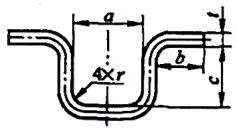 | L=a+2b+2c+1,2t |
| 7 | Piegare per formare quattro angoli in due tempi. | L=a+2b+2c+1,2t |
3.3 Calcolo delle dimensioni non piegate per le parti piegate a cerniera
Per il tipo a cerniera parti di piegatura con r= (0,6~3,5)t (fare riferimento alla Figura 5-10), il processo di flangiatura segue di solito l'andamento mostrato nella Figura 5-11. Durante la flangiatura, lo spessore della lamiera aumenta e lo strato neutro si sposta verso l'esterno. Le dimensioni del grezzo non piegato possono essere calcolate approssimativamente con la seguente formula:
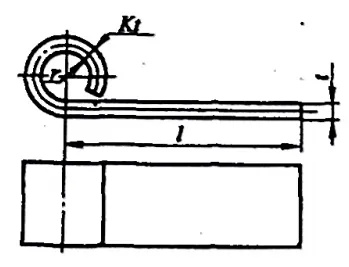
- a) Prima operazione
- b) Seconda operazione
L=l+1,57π(r+Kt)+r
Dove:
- L - Dimensioni del fustellato non piegato (mm);
- l - Lunghezza del segmento rettilineo (mm);
- r - Raggio interno di curvatura del pezzo grezzo (mm);
- K - Coefficiente di spostamento dello strato neutro. Quando r/t=0,5~1,8, K è solitamente considerato 0,5~0,70 (minore è il valore di r/t, maggiore è il valore di K; viceversa, minore è il valore di K). Può anche essere selezionato in base alla Tabella 5-4.
Tabella 5-4 Coefficiente di spostamento dello strato neutro per parti in flessione di tipo a cerniera
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |