1.曲げスプリングバック
あらゆる塑性変形と同様に、チューブの曲げ加工も弾性変形を伴う。荷重を取り除くと、曲げ中立層の外側にある繊維は弾性回復により短くなり、内側にある繊維は長くなるため、曲げ速度と曲げ角度が変化する。この現象をスプリングバックという。スプリングバックには、図4-25に示すように2つの形態がある。
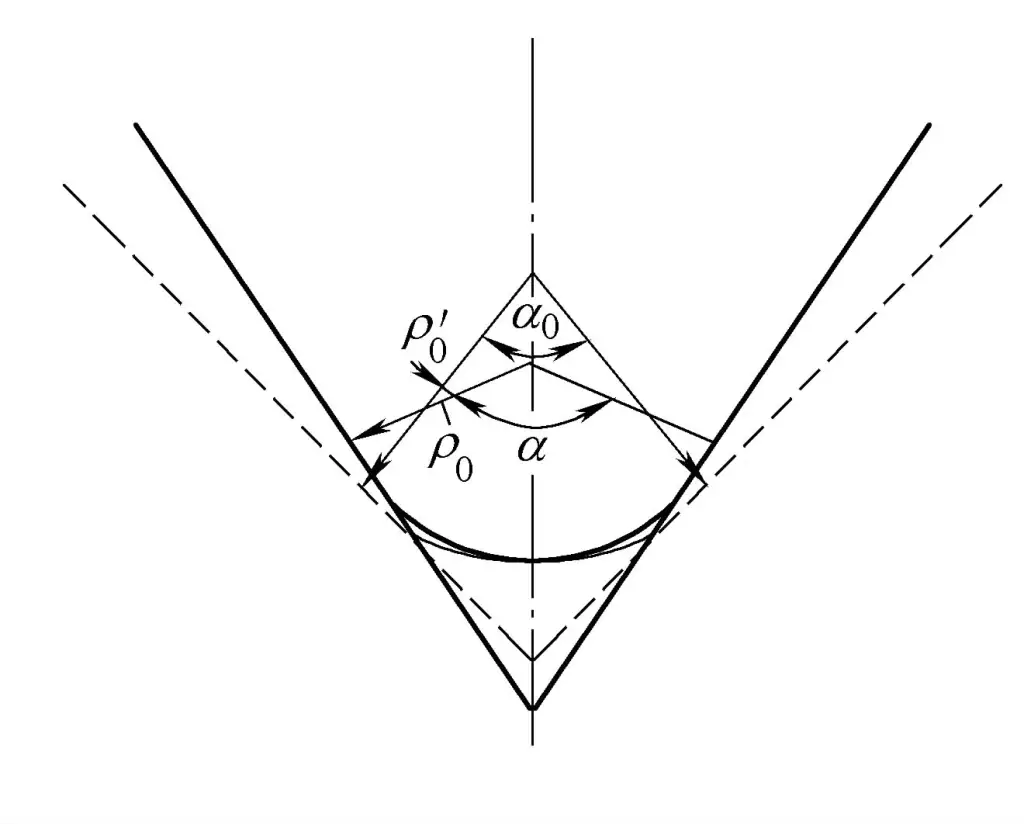
1) 曲率が減少する。
曲率は1/ρから減少する。0 荷降ろし前に1/ρ'0 荷降ろし後
2) 曲げ角度が減少する。
曲げ角度は除荷前のαからαに減少する。 0 除荷後スプリングバックの大きさは、曲率の変化ΔKまたは曲げ角度の変化Δα(スプリングバック角とも呼ばれる)によって計算することができます。
Δα = α - α 0
(1) 曲げスプリングバックに影響する要因
曲げ加工において、スプリングバック量に影響を与える要因は数多くあるが、主な要因は以下の通りである:
1) ブランクの機械的特性。
σの値が小さいほどs /E、つまりσが小さいほどs Eが大きいほど、スプリングバック値Δαは小さくなる。
2) 変形の程度 r/t.
同じ条件下では、r/tが小さいほど曲げ変形の程度が大きくなり、全変形に占める弾性変形の割合が減少するため、曲げのスプリングバックが減少する。
3) 屈曲中心角α。
曲げ中心角αが大きいほど、変形領域の長さは長くなる。同じ変形条件では、単位長さあたりの変形量は減少する。したがって、曲げ角度αが大きくなるほど、全変形量に占める弾性変形の割合が大きくなり、スプリングバック値Δaも大きくなります。
4) ダイ・クリアランス Z.
より大きい ダイ・クリアランススプリングバックが大きい。
5) 曲げ方式。
スプリングバック量は、ドロー曲げ工程では小さく、プッシュ曲げ工程では最も小さい。
6) ワーク形状と材料組織の状態。
複雑な形状、複数の相互引っ張りにより、スプリングバックが小さく、冷間加工硬化後にスプリングバックが大きくなる。
7) 金型構造とプレス力の大きさ。
エッジを押す力が大きいため、ワークが曲がった後の反発量が小さい。
(2) リバウンド値の決定
ワークの反発値を決定することは、反発を克服するための対応策を講じることであり、曲げ加工されたワークが設計パターンの精度要求を満たすことができるようにすることである。リバウンド値を決定する方法には、ルックアップチャート法、ルックアップテーブル法、計算法などがあります。
実際のところ 曲げ成形一方、形材の曲げ加工中に中立層を正確に決定することは困難であり、反発の計算をより難しくしている。形材曲げの反発計算は、板材曲げの反発計算よりもはるかに複雑である。 チューブ曲げ はすべて概算であり、実際の状況とは大きな差がある。
現在、国内外でリバウンドに関する研究が進められている。反発には様々な要素が絡み合い、非常に複雑であるため、正確な計算式は今のところ存在しない。そのため、反発値の管理は、一般的に構造の異なる金型を用いて、主に金型試験時に補正している。
(3) リバウンドの低減および防止方法
リバウンドを低減・防止する方法は、原理的な観点から大きく2つに分けられる。第一のカテゴリーは、変形を大きくすることによってリバウンド後の部品の形状を確保する方法である。このカテゴリの主な対策は、金型の形状を修正したり、部品の曲げ曲率を小さくしたり、曲げ角度を大きくしたりして、リバウンド後の部品が設計要件を満たすようにすることです。
もう一つのカテゴリーは、曲げ変形部の応力分布を変えることでリバウンドを抑える方法です。このカテゴリーでは、接線方向の引張応力を加え、曲げ変形部断面の応力分布を均一にすることで、除荷時の弾性回復の不均一を抑え、リバウンド量を低減する方法が最もよく使われます。
曲げ成形におけるリバウンドは、部品の寸法精度と生産効率に影響を及ぼす主な要因の一つである。リバウンドの予測は成形プロセス全体と密接に関係しているため、リバウンドの問題は非常に複雑であり、曲げ成形の研究におけるホットで困難なポイントとなっています。 プロファイル曲げ フォーミング国内外の多くの学者が綿密な調査と議論を行ってきた。
現在、管の曲げ加工におけるリバウンドの問題に対処する方法はいくつかある:
1) 経験に基づくリバウンドデータ表をリストアップする。
例えば、いくつかの国内造船所はCNCを購入している。 パイプ曲げ機 アメリカのWALLACE COAST社製で、リバウンド補正のために制御システムに設定された経験データを使用する。しかし、この方法の誤差が大きいため、CNCパイプ曲げ機の曲げ精度は理想的ではありません。
2) 理論的な計算方法を用いる。
パイプ曲げ時の力の状況は非常に複雑であり、計算時に仮定や単純化を行う必要があり、材料特性や実際の作業条件を予測することは困難であるため、これまでのところ、リバウンド理論計算式を実際に使用して成功した前例は見つかっておらず、さらなる議論が必要である。
3) 航空機や自動車の製造業界では、アメリカのイートン・レオナード社に代表される方法が長年使われてきた。
この方法では、パイプ曲げのリバウンドに影響する要因はたくさんあるが、工作機械を調整すれば、プロセス・パラメーター(曲げ半径曲げ角度、曲げ速度、クランプ力など)を決定し、このとき、素材パイプを一括して曲げた状態で、曲げ角度とリバウンド後の成形角度の関係を測定する。したがって、パイプ曲げ機のアームの旋回角度とパイプの成形角度は、直線的な関係とみなすことができる。
この方法は、パイプ曲げ機でパイプを125°と22°で曲げ、パイプを曲げた後、CNCパイプ形状測定機の上に置いて、実際の成形角度を120°と20°として測定し、2点を通る直線方程式を確立することで、パイプ曲げ機のアームの回転角度とパイプの必要な成形角度の関係を得ることができます。この方法は良い効果がある。
パイプ曲げのリバウンド問題を解決するために、以下の作業が行われた:
1)多くのリバウンド実験が行われた。
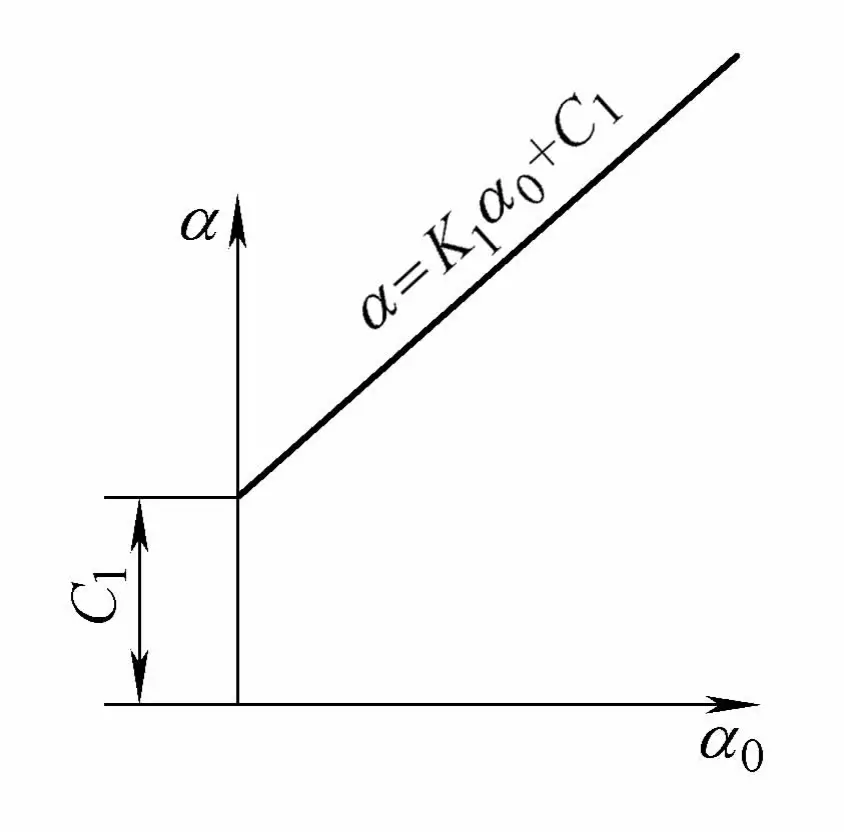
複数のパイプ曲げ機で様々な仕様のコアレスおよびコア付きパイプの曲げ実験を行い、測定データに対して回帰分析計算を行うことにより、曲げ角度αおよび成形角度αが、曲げ角度αと成形角度αとの間に相関関係があることがわかった。 0 これは線形変化の理論計算と一致する。しかし、異なっているのは、この直線は原点を通らず、区間距離C1 図4-26に示すように。
α = K1 α0 + C1
式中、K1 は直線の傾きである;
C1 は直線の切片である。
上式から、以下の結論が導かれる:同じバッチの材料から曲げ加工されたチューブの場合、工学的な曲げ角度の範囲内では、曲げ角度αと成形角度αの関係は、次のようになる。 0 は常に原点を通らない直線である。
2) チューブ曲げスプリングバック実験の理論解析。
スプリングバック実験の結論の正しさを分析するため、管曲げ機の作業条件について力解析を行い、いくつかの仮定と単純化を行った後、大量の計算を行った。
計算の結果、曲げ角度の小さい範囲では、曲げ角度αと成形角度αの関係は、曲げ角度αの方が成形角度αよりも大きいことがわかった。 0 が湾曲し、曲げ角度が1より大きくなった後、曲げ角度αと成形角度αの関係は、次のようになる。 0 これは、実験中に観察された直線関係と同じ傾向を示しており、スプリングバック実験の結論が正しいことを示している。
この2つの値には大きな差があるが、これは理論計算における仮定と単純化、および実際のチューブの曲げ条件が計算よりもはるかに複雑であることに起因している。
したがって、上記の研究は、「管曲げ機のアームの旋回角度と管の曲げ角度の関係を直線的なものとみなす」EATON LEONARD社に代表される研究結果よりも深い。
まとめると、管材の曲げスプリングバックの問題に対処するための現在の最良の方法は、次のとおりです:管材のバッチを曲げる場合、所定の管曲げ機で2つの異なる曲げ角度(たとえば30°と90°)の実験を行うことができます。実験中、管材曲げ機のアームの2つの実際の回転角度αを記録する。1 , α2 そして、チューブの2つの成形角αを測定する。01 , α02 .次に、以下の式を使って係数を計算する。
K1 = (α 2 - α 1 )/ (α 02 - α 01 )
C1 = α 1 - α 1 (α 2 - α 1 )/ (α 02 - α 01 )
上記の2つの式をリバウンド実験のαの式に代入することで、得られる一次方程式がそのバッチのパイプ材料のリバウンドルールとなる。
2.曲げ伸び
曲げ機械で曲げた後、ある長さのパイプの軸方向の長さが長くなる。軸方向長さの増加はパイプの伸びと呼ばれる。曲げ伸びは部品の寸法精度に影響する。この問題を解決するために、過去に用いられた方法には次のようなものがある:
1) 経験に基づく伸びのデータ表が生産用に作成されたが、この方法を使用すると誤差が大きい。
2) パイプの曲げ伸びの理論に関する計算方法。リバウンドと同様、理論的な計算式で実際にうまく使われているものは今のところなく、さらなる議論が必要である。
3) 航空機や自動車製造業界では、イートンレオナード社に代表される方法が長年使用されている。すなわち、CNCチューブプロファイラで反発を測定しながら、いわゆるアーク定数を計算式で算出し、曲げ角度が100°のときに使用される材料長であり、また、パイプの伸びは成形角度に正比例すると考えられている。
パイプ曲げの伸びの問題を解決するために、以下の作業が行われた:
1) 多数の伸長実験が行われた。
5つの造船所の複数のベンディングマシンでコアレスおよびコア入りの様々な仕様の曲げ実験を行い、各バッチの材料から得られたデータについて回帰分析計算を行った結果、伸び△Lは成形角度α'と原点を通らない直線関係にあることがわかった。すなわち
ΔL = K 2 α'+C 2
式の中で、
- K 2 - 直線の傾き;
- C 2 - 直線。
測定データの回帰分析により、相関係数γは0.97~0.99となり、明確な直線関係が示された。したがって、以下の結論が導き出される:同じバッチの材料の管について、工学的な曲げ角度の範囲内では、伸びΔLと成形角度α'は、原点を通らない直線関係にある。
2) 関連造船所のスプリングバック・データ表についても回帰検証を行った。
経験的な計算から、伸びΔLと成形角度α'も直線関係にあることが知られており、相関係数γは0.99以上で高い直線性を示すが、切片は一般に小さい。
3) パイプ曲げ伸び実験の理論的解析。
伸び実験の結論の正しさをさらに証明するため、パイプベンダーのパイプ曲げ条件について力解析を行い、いくつかの仮定と単純化を行った後、大量の計算を行った。計算の結果、曲げ角度が小さい範囲では、伸びΔLと成形角度α'は曲線的な関係を持ち、曲げ角度が3°を超えると、伸びΔLと成形角度α'は直線的な関係を持つことがわかった。
理論解析の線形関係部分と実験中の線形関係の傾向は同じであり、これはパイプ曲げ伸び実験の結論の正しさを証明している。両者の値には大きな差があることに注意すべきであるが、これは理論計算の仮定と単純化、および実際のパイプ曲げ条件が計算された状況よりもはるかに複雑であることに起因する。
本研究の結論は、同一材種の管について、工学的な曲げ角度の範囲内では、伸びΔLと成形角度α'は原点を通らない直線関係を有するというものであり、伸びと成形角度が正比例するという従来の考え方とは異なり、前者の方がパイプベンダーによる管曲げの実態に即している。
要約すると、パイプ材料の曲げ伸びの問題に対する現時点での最良のアプローチは、次のようになるはずである。パイプ材料のバッチを曲げる場合、同じ長さLで曲げ角度が異なる2つの曲げ実験(例えば、30°と90°)を所定のパイプベンダーで行うことができる。実験後、パイプを取り外し、2つの実際の成形角度α'を測定する。 1 , α' 2 と、実際の2本のパイプ軸の長さL'の増加分である。 1 , L' 2 そして、伸びを計算することができる。
δl1 = (l1 '-l) δl2 = (l2 '-l)
このことから、ΔLに関係する一次方程式の係数は、以下の2つの式を用いて計算することができる。
K 2 = (ΔL 2 -ΔL 1 )/ (α' 2 -α' 1 )
C 2 = ΔL 1 -α' 1 (ΔL 2 -ΔL 1 )/ (α' 2 -α' 1 )
上記の2つの式をΔLに関する一次方程式に代入することで、このバッチのパイプの伸び則が得られる。インテリジェントパイプ曲げ測定器は、この伸び則を簡便に求めることができる。
3.パイプ曲げ後の成形半径とスプリングバックの問題への対処法
パイプ材が曲げられてはね返った後、その成形半径R'は金型半径Rより大きくなり、パイプの接点が変化する。したがって、パイプを曲げる場合、曲げ機械はこれによって生じる曲げ開始点の変化を考慮する必要がある。EATON LEONARD社が採用している方法は、CNCチューブプロファイラを使用してスプリングバックの関連パラメータを測定し、スプリングバック後の成形半径を計算式で算出し、この算出半径を使用して開始曲げ点を補正する方法です。
この計算式で曲げ開始点を求めると、規格の小さいパイプ(3mm未満など)を曲げる場合は、誤差が大きくなるものの、まだ使用可能であり、規格の大きいパイプを曲げる場合は、特に誤差が大きくなり、その効果もよくないことがわかった。これは、パイプ曲げ加工時の状況が非常に複雑であり、材料特性や実際の作業条件を予測することが難しいため、成形半径の理論計算式が実際のニーズに対応できないためでもある。
曲げ開始点がうまく処理されないと、曲げ成形精度の確保が難しくなり、ノーマージン曲げ加工を実施する際に困難が生じる。この問題を解決するためには、最新の測定器を使用すべきである。
あるパイプ曲げ機を対象として、パイプ材料の曲げとスプリングバック後の成形半径を実際に測定し、工程内の曲げ開始点を処理する基礎となる。インテリジェントパイプ曲げ測定器は便利にパイプ材料の曲げとスプリングバック後の成形半径を得ることができ、測定の計算原理は次の計算式に示されている。
4.インテリジェントパイプ曲げ測定器によるスプリングバック、伸び、成形半径の測定方法
インテリジェントパイプ曲げ測定器は、主に上記のパイプ曲げ原理に基づいており、CNCパイプ曲げ機で使用するために特別に開発されました。測定器は、測定装置(測定機構、角度センサーを含む)とマイクロコンピュータシステム(マイクロコンピュータ、インタフェースボードを含む)で構成されています。角度0.1°、長さ0.25mmと高精度です。
本測定器の測定機構は、図4-27に示すような4本の棒からなる平面機構であり、節点a、b、cに角度センサーが設置され、隣接する2本の棒の間の角度を測定することができる。dとeの測定ヘッドは平面であるため、測定中、ロッドadとbeはdghe管の直管部分に対して垂直になることができる。
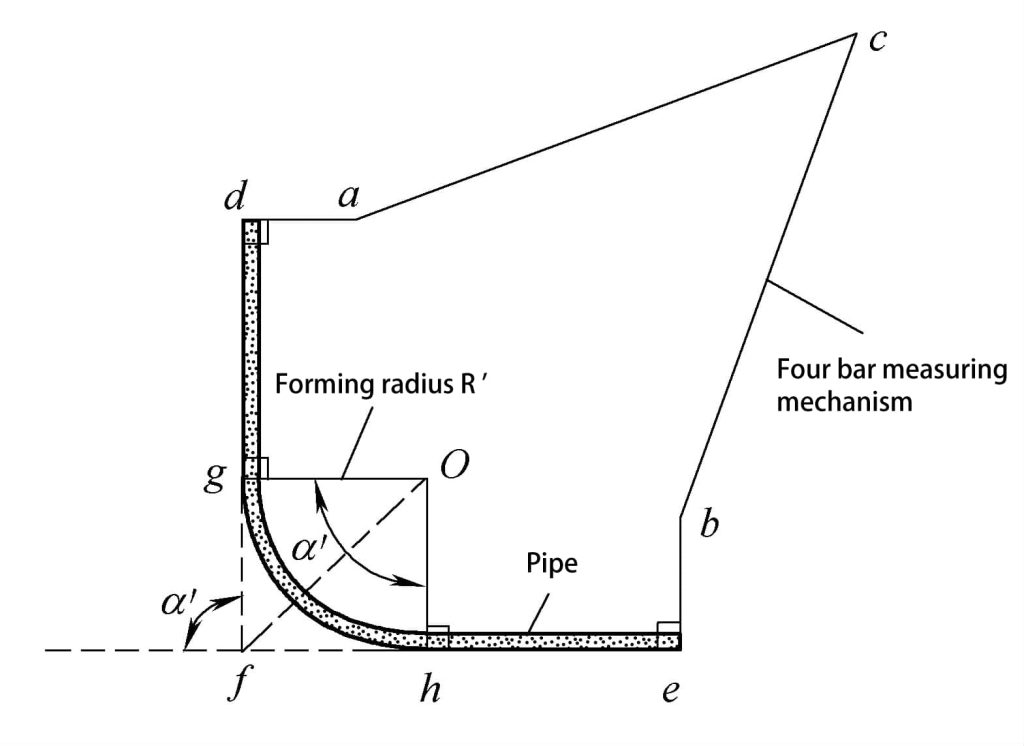
4本バーの平面機構の各ロッドの長さは既知であるため、dgheパイプの関連する幾何学的パラメータを測定し、計算することができる。その方法は以下の通りである:
1) 機構の既知の条件と角度センサーによって測定された角度に基づいて、パイプの成形角度α'を計算することができる。
2) 既知の機構条件と角度センサーで測定された角度に基づき、直管軸の交点の距離dfとfeを計算することができる。
3) パイプの折り曲げ開始点からの距離dgが0.5mm以下の場合。 フィッティング がわかっていれば、実際の成形半径R'をさらに計算することができる。
R'=O g = (df-dg) / tan(α'/2)
4) パイプ軸の長さL'はさらに計算できる。
L’=df+fe-2R’tan(α’/2) +πR’α’/180
上記の原理と式に基づき、パイプベンダー上で同じ長さLの2つの試験片を、それぞれ距離dとgの曲げ開始点から所定の角度(H 1 =この測定器は自動的に実測を完了し、異なる金属材料とパイプモデルの反発変動パターン、伸び変動パターン、反発後の成形半径を印刷することができます。
また、ワークのパイプ形状が与えられている場合、本装置は、取り代なしで曲げるためのブランキングデータを提供することができ、始点補正とリバウンド補正を含むCNCパイプベンダーの加工プログラムを提供することができます(本装置はパイプ形状を測定する機能も備えています)。計器が提供するデータは、CNCパイプベンダーの成形精度を大幅に向上させるだけでなく、技術進歩を促進し、労働強度の削減、鋼材の節約、生産効率の向上という目的を達成する。
5.曲げ半径
パイプ材の曲げ変形の程度は、相対曲げ半径R/Dと相対厚さt/D(Rはパイプ材の断面中心層の曲率半径、Dはパイプ材の外径、tはパイプ材の肉厚)の値に依存する。R/Dとt/Dの値が小さいほど、曲げ変形の程度が大きくなり、曲げ中立層の外壁は過度に薄くなり、破断に至ることさえある。
同時に、変形の程度が大きくなると、断面の歪み(偏平化)も大きくなる。したがって、パイプ材の成形品質を確保するためには、変形度を許容範囲内に制御する必要がある。パイプ材を曲げ加工する際の許容変形度を曲げ成形限界という。管材の曲げ成形限界は、管材の機械的性質や曲げ方法だけでなく、管継手の使用条件にも依存する。
汎用の曲げ加工部品の場合、成形限界を定義する条件は、最大伸びひずみε マックス 曲げ変形領域の外側の中立層から最も遠い位置で発生する曲げ変形は、材料の塑性が許容する限界値を超えてはならない。
管継手の曲げ変形領域外の外面層に亀裂が生じないという条件下では、限界曲げ半径r 分 管継手曲げの成形限界としては、部品の内側に曲げることができるrが用いられる。 分 は、材料の機械的特性、管継手の構造サイズ、曲げ加工方法、およびその他の要因に関連している。
曲げ加工方法の違いによる最小曲げ半径を表4-6に示す。
表4-6 パイプ曲げ最小曲げ半径(単位:mm)
| 曲げ加工方法 | 最小曲げ半径 (r分) |
| プレス曲げ | (3~5)D |
| ラップ曲げ | (2~2.5)D |
| ロール曲げ | 6D |
| プッシュ・ベンディング | (2.5~3)D |
注:Dはパイプの外径。
鋼管とアルミ管の最小曲げ半径は表4-7に示す。
表4-7 鋼管およびアルミ管の最小曲げ半径(単位:mm)
| パイプ外径 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| 最小曲げ半径 r分 | 8 | 12 | 16 | 20 | 28 | 32 | 40 | 45 | 50 | 56 |
| パイプ外径 | 24 | 28 | 30 | 32 | 35 | 38 | 40 | 44 | 48 | 50 |
| 最小曲げ半径 r分 | 68 | 84 | 90 | 96 | 105 | 114 | 120 | 132 | 144 | 150 |