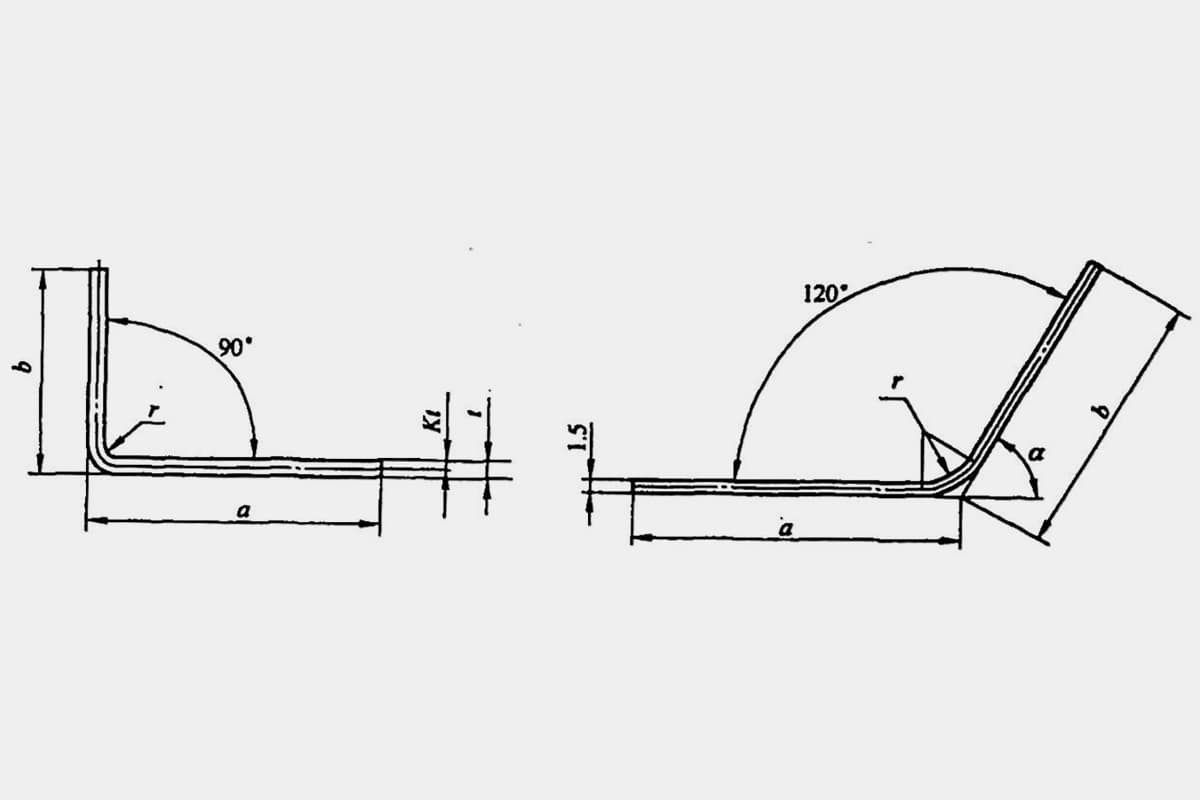
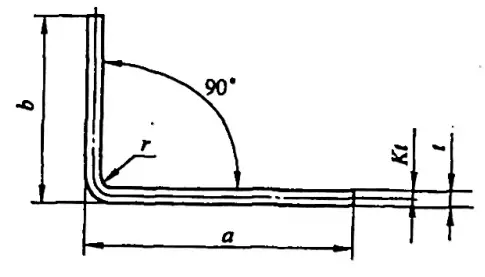
板金曲げ部品の場合、ブランク寸法の算出は曲げ工程計画策定の必須条件です。技術者によって、工程表で選択する曲げ許容係数が異なる場合があり、ブランクサイズの精度は、曲げ部品の寸法精度と製品品質に直接影響します。
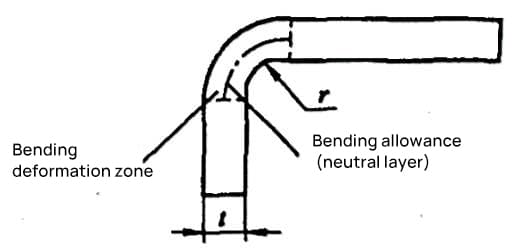
時には、不正確な計算が廃棄物を生んでしまうことさえある。典型的な単純曲げ部品の展開長さL(図5-1参照)は、L=a+b-y(ここでyは曲げ控除であり、R部の補正値としても知られている)である。
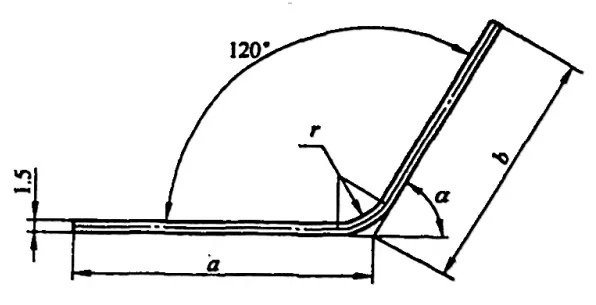
しかし、様々なマニュアルや資料では、φ=90°の曲げ控除は直接求めることができますが、図5-2に示すような90°以外の曲げの場合は、技術者が経験係数(K係数)に基づいて計算する必要があります。
関連記事 板金展開の技術を解説
1.板金曲げの展開寸法の計算原理
曲げられたブランクの展開寸法は、中立層の長さが曲げの前後で変化しないという原則に基づいて決定される。シートメタルが曲げられると、ブランク部分の外層繊維は引き伸ばされ、内層繊維は圧縮される。
外層繊維の伸びは外側から内側に向かって徐々に減少し、内層繊維の圧縮も内側から外側に向かって徐々に減少する。
繊維が伸張から圧縮へ、あるいは圧縮から伸張へ移行するとき、応力とひずみがゼロで、曲げの前後で長さが変わらない繊維の層が存在しなければならない。
この層が、私たちがニュートラル層と定義するものである。したがって、曲げられたブランクの展開寸法を計算する鍵は、中立層の位置を決定することです。中立層の位置は、塑性変形の前後で曲げ部分とブランクの体積が等しいという条件に基づいて決定されます。
2.中立層の曲率半径ρの決定
理論的には、曲げ部の厚み方向に沿った不均一な変形により、中立層は放物面であるが、計算の都合上、通常は円弧面とみなされる。曲げ変形が非常に小さい場合(r/t >6.5)、中立層はおおよそ材料厚みの中央にあると考えることができる。 ρ=r+t/2.
変形が非常に大きい場合(r/t≦6.5)、材料の厚さは薄くなり、図5-3に示すように断面の歪みは非常に大きくなる。
このとき、断面に作用するすべての力の合力がゼロになるという釣り合い条件を満たすためには、中立層は材料の内面に向かって移動しなければならない。
このとき、中立層の曲率半径は、塑性変形時に体積が変化しないという条件、つまり曲げる前の体積から求めることができる:V0=LBtであり、曲げ後の体積である:
V=(R2-r2)α*B'/2。
式中、Bはブランクの幅(mm)、B'は曲げ後のブランクの平均幅(mm)、αは曲げ中心角である。曲げの前後で体積が等しくなる原理から、V0=つまりVだ、
LBt=(R2-r2)α*B'/2、L=(R2-r2)α*B'/2tB (5-1)。
中立層の応力とひずみがゼロであることから、L=l=αρが得られる。ここで、Lは中立層の変形前の長さ(mm)、lは中立層の変形後の長さ(mm)である。
式(5-1)を代入すると、次のようになる。 ρ=(R2-r2)B'/2tB.上の式にR=r+t'を代入すると、別の形の式が得られる。 ρ=(r/t+η/2)tβη (5-2)ここで、βは幅係数、β=B'/Bであり、一般に幅の広い板(B>3t)が曲げられる場合、通常β=1とみなされる;ηは薄化係数、η=t'/tである。
式(5-2)は中性層の位置を理論的に計算する式である。計算の際には、η、すなわち間引きの法則を知る必要がある。ηの値は表5-1を参照されたい。
薄肉化ルールは非常に複雑であり、曲げ領域における中立層の位置の分布は一様ではなく、また薄肉化ルールは曲げ方法、曲げ下金型の溝幅、材料の厚さなど多くの要因に関係していることを指摘しなければならない。
このため、中立層の位置の理論計算には避けられない誤差が生じ、理論的な決定方法の実用的な応用価値が低下する。
表5-1:シンニング係数η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
実際の生産現場では、中立軸の位置を決めるのに、理論的な計算よりもわかりやすい経験式が一般的に使われる:
ρ = r + Kt (5-3)
どこでだ:
- ρ - 中立軸の曲率半径(mm)
- r - 素材の内側曲げ半径(mm)
- t - 素材の厚さ(mm)
- K - 中立軸係数(経験値 K因子を参照。
表5-2:中立軸係数Kの経験値
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
注:
- K1 は、トッププレートまたはプレスプレートによるV字型またはU字型のベンドに適用されます。
- K2 は、トッププレートのないV字型ベンドに適しています。
3.いくつかの典型的なシートメタルベンドに対するブランクの折り曲げなし寸法の計算
中立層の定義に基づけば、ブランクの展開寸法は中立層の長さに等しいはずである。一般的に、内側の 曲げ半径 r>0.5tの場合は角丸ベンド、r<0.5tの場合は非角丸ベンドとなる。
さらに、板幅Bによって広板ベンドと狭板ベンドに分類され、板幅B>3tの場合を広板ベンド、板幅B<3tの場合を狭板ベンドと呼ぶ。
生産現場では、角丸半径(r>0.5t)と幅広板(B>3t)の曲げが最も広く使用されており、曲げの普遍性を考慮して、ここでは主に角丸半径と幅広板の曲げ時のブランク展開寸法の計算について述べる。
3.1 丸角ベンド(r>0.5t)のブランク展開寸法の計算
r>0.5t、B>3tの場合、曲げ部の薄肉化がひどくなく、断面の歪みが小さいため、ブランクの長さは、中立層の長さがブランクの展開寸法に等しいという原則に基づいて決定することができる。
角丸曲げ(r>0.5t)のブランク展開寸法を計算する一般的な方法は、曲げ係数の計算と曲げ控除値の計算に分けられる。
1.角丸曲げ(r>0.5t) ブランクの折り目なし寸法に対する曲げ係数の計算:
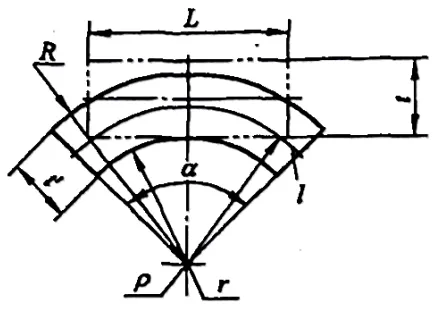
1) 曲げ係数とは、図5-4に示すように、曲げ変形部の中立層(曲げR部)に沿って測定した円弧部の長さをいう。
曲げ係数は式(5-4)で計算される: x=παρ/180° (5-4)
ρは中立層の曲率半径(mm)。
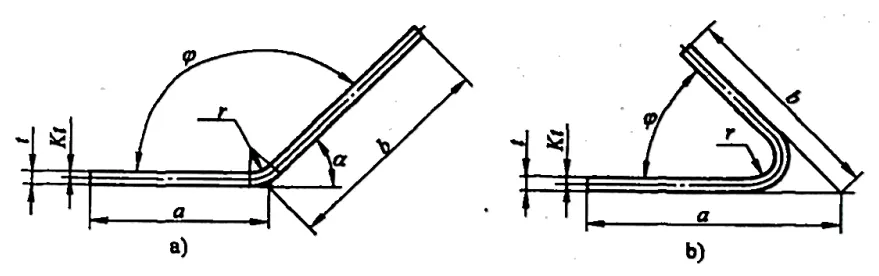
2) 図 5-5 にブランク展開寸法の曲げ係数算出のための寸法表記例を示すが、ブランク展開寸法の曲 げ係数の算出式は次のとおりである。

a) φ > 90° b) φ≤90
L=a+b+x (5-5)
式(5-3)を式(5-4)に代入すると、曲げ係数の式が得られる:
x=πα(r+Kt)/180° (5-6)
式(5-6)を式(5-5)に代入すると、曲げブランクの展開サイズの計算式が得られる:
L=a+b+πα(r+Kt)/180° (5-7)
どこでだ:
- L - ブランクの展開サイズ(mm);
- K - K係数の係数で、その値は表5-2を参照;
- α-曲げの中心角で、曲げ部分の角度との関係はα=180°-φ;
- r - ブランク内層の曲げ半径(mm);
- t - 素材の厚さ(mm);
- a, b - それぞれ部品の直線部分の長さ(mm)。
2.角丸曲げ部品(r>0.5t)の展開サイズに対する曲げ控除額の計算
1) 曲げ減点(R部の補正値ともいう)は、図5-6に示すように、曲げ変形部(曲げのR部)のRの2倍と曲げ係数の差である。

曲げ控除(R部分の補正値)は、式(5-8)に従って計算される:
y = 2R-παr/180° (5-8)
2) 図 5-7 にブランクの展開サイズに対する曲げ控除計算のための寸法注釈の例を示す。曲げ減点yは以下の式で計算される:
a)90°<φ≦165° b)φ≦90
φ≦90°のとき:
R=(r+t)/tan(φ/2)
上式と(5-3)式を(5-8)式に代入すると、曲げφ≦90°の場合の曲げ控除(すなわちR部の補正値)が得られる(図5-7b参照):
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
90°<φ≦165°の場合:
R=(r+t)tan[(180°-φ)/2]
上式と式(5-3)を式(5-8)に代入すると、90°<φ≦165°の曲がりに対する曲げ減点(すなわちR部の補正値)が得られる(図5-7a参照):
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
165°<φ≦180°のとき:
y≈0
3) 図5-7に示す部品のブランク寸法の曲げ控除値の計算式は次の通りである:
L=a+b-y (5-11)
φ≦90°のとき、式(5-9)を式(5-11)に代入すると、ブランク寸法の曲げ減点値の計算式は次のようになる:
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
90°<φ≦165°のとき、(5-10)式を(5-11)式に代入すると、ブランク寸法の曲げ減点値の計算式は次のようになる:
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
165°<φ≦180°のとき:
L≈a+b (5-14)
どこでだ、
- y - 曲げ控除(mm)
- L - ブランク寸法(mm)
- r - ブランクの内側曲げ半径(mm)
- t - 素材の厚さ(mm)
- α-曲げ中心角、曲げ角度との関係はα=180°-φ。
- a、b-部品の曲げ頂点までの長さ(mm)。
3.マルチアングルベンドのブランクサイズの計算
マルチアングルベンドの場合、ブランクサイズはR部分とストレートエッジの長さの合計となる。
1) 曲げ係数による多角度曲げブランクサイズ計算:
L=l1+l2+...+ln+1+nx (5-15)
l1, l2...ln+1 は各辺の直線部分の長さ(mm)である;
nはベンドRの数。
2) 曲げ控除による多角度曲げブランクサイズ計算:
L=l1+l2+...+ln+1-NY(5勝16敗)
l1, l2...ln+1 は部品の端から曲げ頂点までの長さ(mm);
nはベンドRの数。
例 5-1: 図 5-8 に示す曲げのブランク・サイズを計算する。
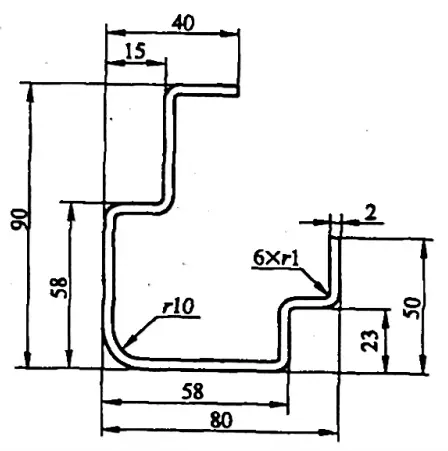
解決策1:曲げ係数を用いてブランクサイズを計算する。
付録A参照:曲げピース角度φ=90°、厚さt=2mm、半径r=10mmの場合、曲げ係数は2.68mm;
曲げピースの角度が90°、厚さt=2mm、半径r=10mmの場合、曲げ係数はx2=16.9mmとなる。
式(5-5)と式(5-15)から、曲げピースのブランクの平面サイズは次のように計算される:
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2.68 + 16.9]mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240.98mm。
解決策2:曲げ控除値を用いてブランクの平面サイズを計算する。
付録C参照:角度φ=90°、厚さt=2mm、半径r=1mmの曲げの場合、R部の補正値はy1=3.32mm、角度φ=90°、厚さt=2mm、半径r=10mmの曲げの場合、R部の補正値はy2=7.1mm。
曲げられた部分の生サイズは、式(5-11)と(5-16)から求めることができる:
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3.32 - 7.1] mm
= (25+34+17+116+25+24+27-19.92-7.1) mm
= 240.98 mm
例 5-2: 図 5-9 に示す曲げ部分の生サイズを計算する。
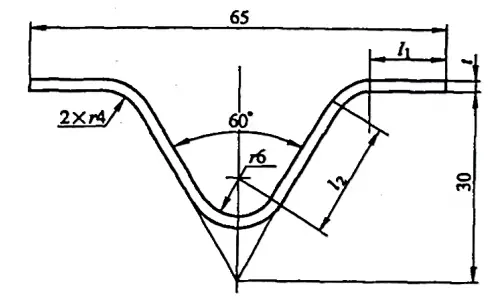
解答曲げ係数を用いて生サイズを計算する。
式(5-5)と式(5-15)から曲げ部のブランク寸法を計算する式は次のようになる:
L=2l1+2l2+2x1+x2
ここで1 = [32.5 - (30tan30°+4tan30°)] mm = 12.87 mm
そして2 = [(30/cos30°) - (8/tan30°+4tan30°)] mm = 18.47 mm
付録Aを参照:曲げ角度φ=120°、t=2mm、r=4mmの場合、曲げ係数の値はx1=曲げ角度φ=60°、t=2mm、r=6mmの場合、曲げ係数の値はx2=14.16mm。
これらの値を式に代入すると、ブランクの展開長さはL= (2×12.87 + 2×18.47 + 2×4.98 + 14.16) mm = 86.8mmとなる。
精度の要求が低い単純な曲げ加工では、ブランクの展開寸法を直接計算できることに留意すべきである。しかし、より複雑な曲げ加工や、より高い精度が要求される曲げ加工では、展開されたブランクの形状と寸法を確認するために、繰り返し試験を行い、継続的に修正する必要があります。
3.2 シャープベンド部品(r<0.5t)のブランク展開寸法の計算
部品の曲げ半径rが0.5t未満の場合、シャープベンドと呼ばれる。このような部品のブランク展開寸法の計算は、曲げ前後の体積整合性の原則に基づいています。
鋭角曲げの場合、曲げ部での材料の減肉が激しいため、変形過程が非常に複雑となり、ブランク展開寸法を正確に算出することが困難となる。そのため、計算されたブランク展開寸法は、経験的データに基づくか、試曲げによって補正する必要がある。
シャープベンド部品(r<0.5t、φ=90°)のブランク展開寸法の計算式は表5-3にある。
表5-3 シャープベンド部品(r<0.5t、φ=90°)のブランク展開寸法の計算式(単位:mm)
| シリアル番号 | 曲げの特徴 | 概略図 | フォーミュラ |
| 1 | コーナーを曲げる。 |  | L=a+b+0.4t |
| 2 | 平らにする。 |  | L=a+b-0.43t |
| 3 | 一度に2つの角を曲げる。 | 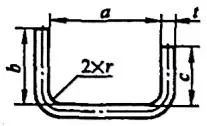 | L=a+b+c+0.6t |
| 4 | 3つの角を同時に曲げる。 | 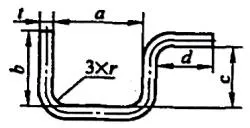 | L=a+b+c+d+0.75t |
| 5 | 最初の例では2つの角を曲げ、2番目の例では別の角を曲げる。 | L=a+b+c+d+t | |
| 6 | 四隅を同時に曲げる。 | 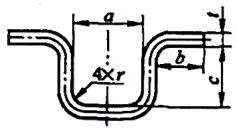 | L=a+2b+2c+1.2t |
| 7 | 曲げて四隅を形成する2つの例。 | L=a+2b+2c+1.2t |
3.3 ヒンジ式曲げ部品の展開寸法の計算
ヒンジタイプの場合 曲げ部品 r=(0.6~3.5)t(図5-10参照)の場合、フランジ加工は通常、図5-11に示すパターンに従う。フランジ加工中、板金の厚みは増加し、中性層は外側に移動する。ブランクの展開寸法は、次式で近似的に計算できる:
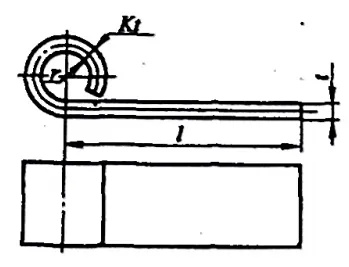
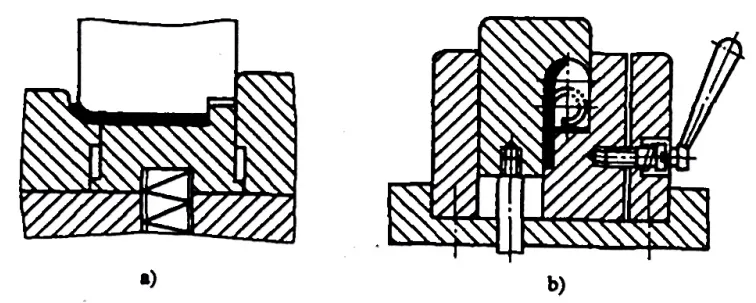
- a) 最初の手術
- b) 2回目の手術
L=l+1.57π(r+Kt)+r
どこでだ:
- L - ブランクの展開寸法(mm);
- l - ストレートセグメントの長さ(mm);
- r - ブランクの内部曲げ半径(mm);
- K - 中立層の変位係数。r/t=0.5〜1.8のとき、Kは通常0.5〜0.70とされる(r/tの値が小さいほどKの値は大きくなり、逆に小さいほどKの値は小さくなる)。また、表5-4に従って選択することもできる。
表 5-4 ヒンジ型曲げ部品の中立層の変位係数
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |