板金部品展開図の作成過程では、加工材料の板厚の影響も考慮する、つまり適切な板厚調整を行う必要がある。
一般的に、板厚が3mm以下のシート材の場合、板厚調整は不要です。板材の中心径、または内外面の切断線から計算できます。成形後の寸法は許容偏差範囲内です。板厚が3mmを超える場合は、板材の中心径で計算する。説明の便宜上、以下の開発材は板材の中心径で計算する。
1.円筒シェル開発計算
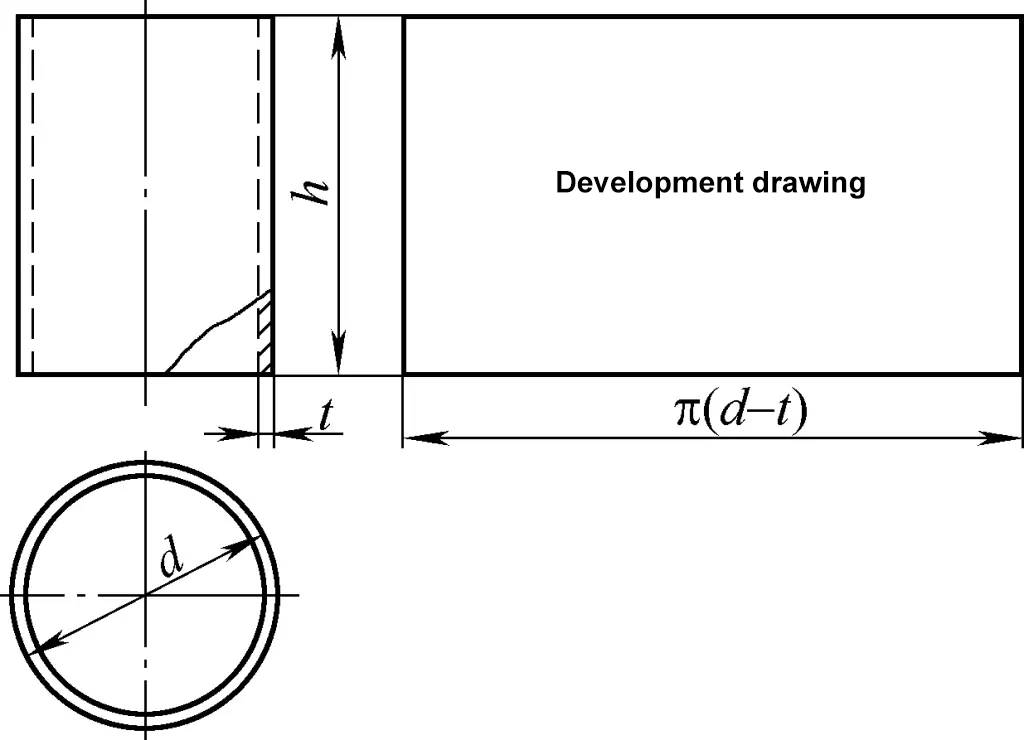
円筒殻は円筒面に属し、その展開図は長方形である。図1に示すように、長方形の一辺は円筒の円周π(d-t)に等しく、もう一辺は円筒の高さhである。図中、dは円筒の外径、tは板厚である。
2.直円錐台の開発計算
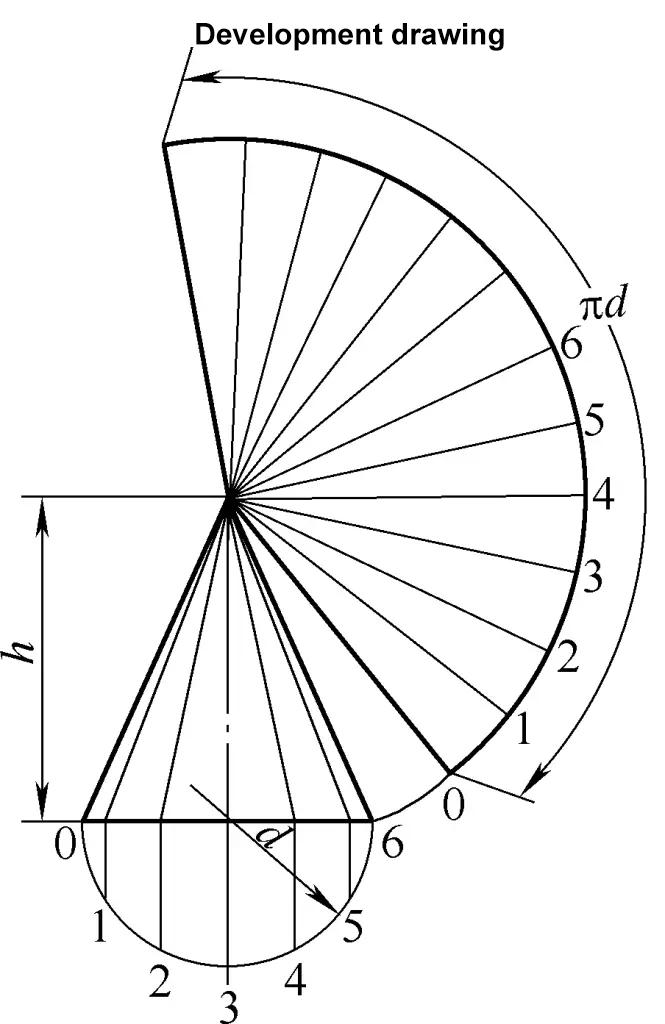
右円錐の展開図はセクター・アークである。図 2 に示す右円錐の展開図の計算式は次のとおりである:
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
式中
- R - セクターアークの半径(mm);
- α - セクター角度(°);
- L - セクターアークのコード長(mm)。
3.切頭直円錐の開発計算
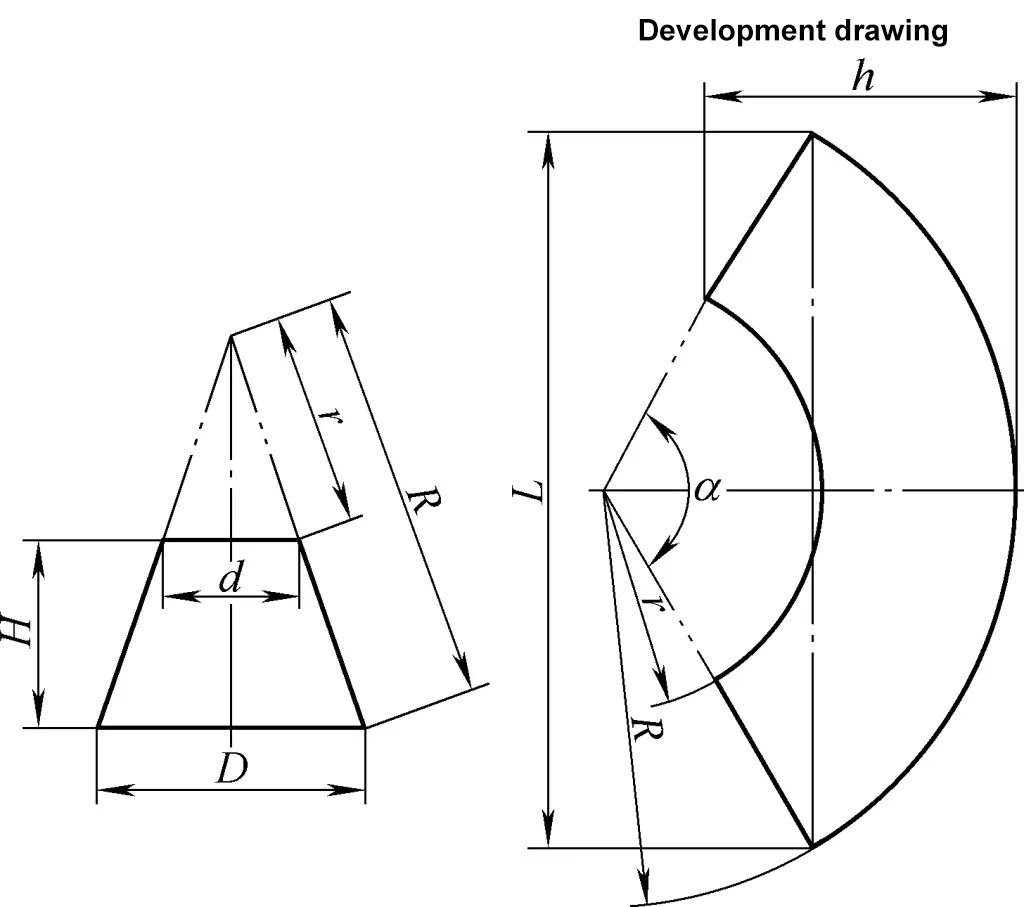
切り捨てられた右円錐の展開図は、同心セクタ円弧である。図3に示す切頭右円錐の展開図の計算式は次のとおりである:
R=√{(D/2)2+DH/(D-d)]である。2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
α>180°のとき、h=R+rsin[(α-180)/2]となる。
式中の記号の意味については、図3を参照のこと。
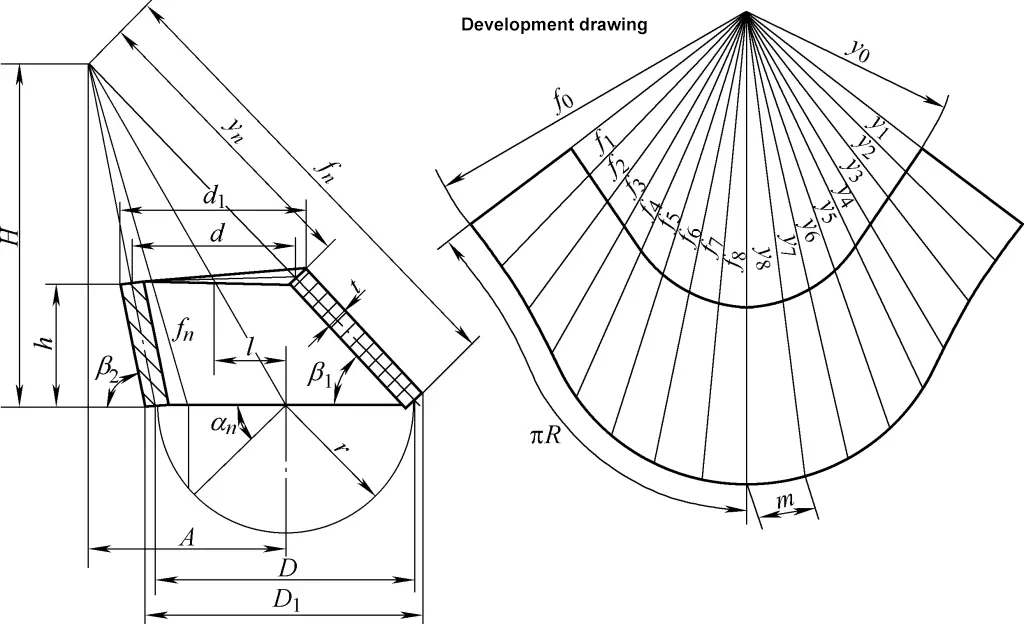
4.斜め右円錐の展開計算
斜め右円錐の展開図は不規則なセクター円弧である。図4に示す斜め右円錐の展開図の計算式は以下の通り:
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[A-D/2cosαn)2+(D/2)2罪2αn+H2]
yn=fn(1-h/H)
m=Dsin(180°/n )
式中
- D1, d1 - 大端と小端の外径(mm);
- D, d - 大端と小端の中心径(mm);
- h - 中心の高さ(mm);
- l - 偏心距離(mm);
- n - 円周の分割数。分割数が多いほど計算は複雑になるが、図面の精度は高くなる。一般的に、分割数は表1を参照することができる;
- fn, yn - 斜め右円錐の傾斜線の長さ(mm)。
表1 シートメタル開発部門数
| 現像ピースの半径/mm | 部門数 |
| 50%以内 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| 2000人以上 | 96 |
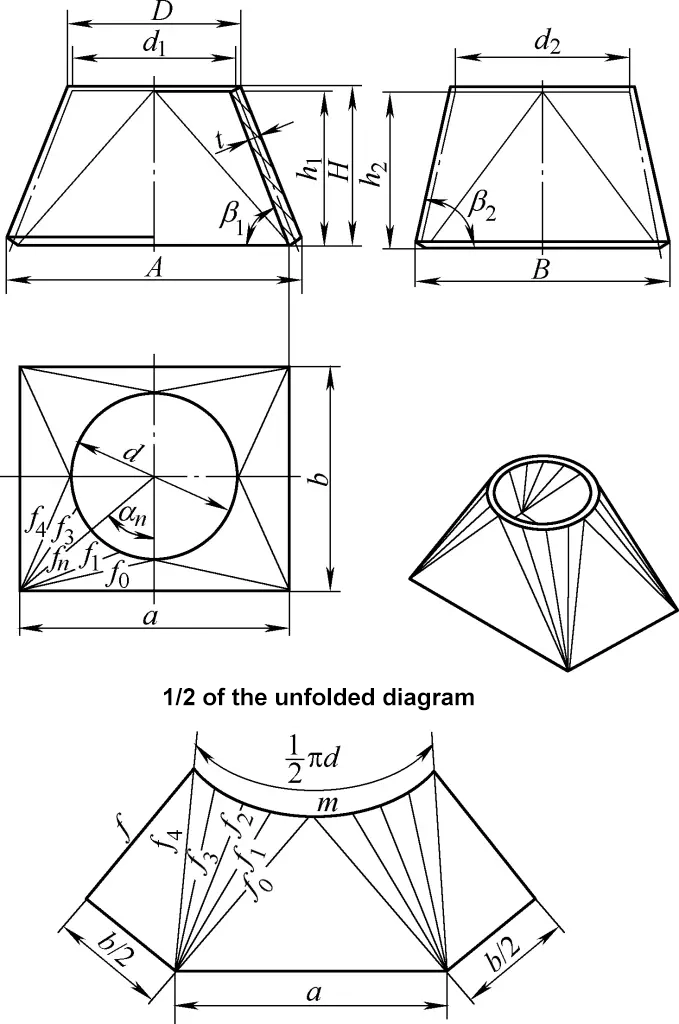
5.正方形から円形への移行ダクトの開発計算
図5に示す直交長方形から円形への移行ダクトは、4つの等しい斜めの直円錐面と4つの対称三角形面から構成される。その展開図の計算式は
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(0<α<90°のとき)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(α=90°のとき)
f=1/2√(a-d)2+4h12]
m=πd/n
式中の記号の意味は図5を参照し、nは円周上の分割数である。一般的には表1の分割数で計算が可能である。