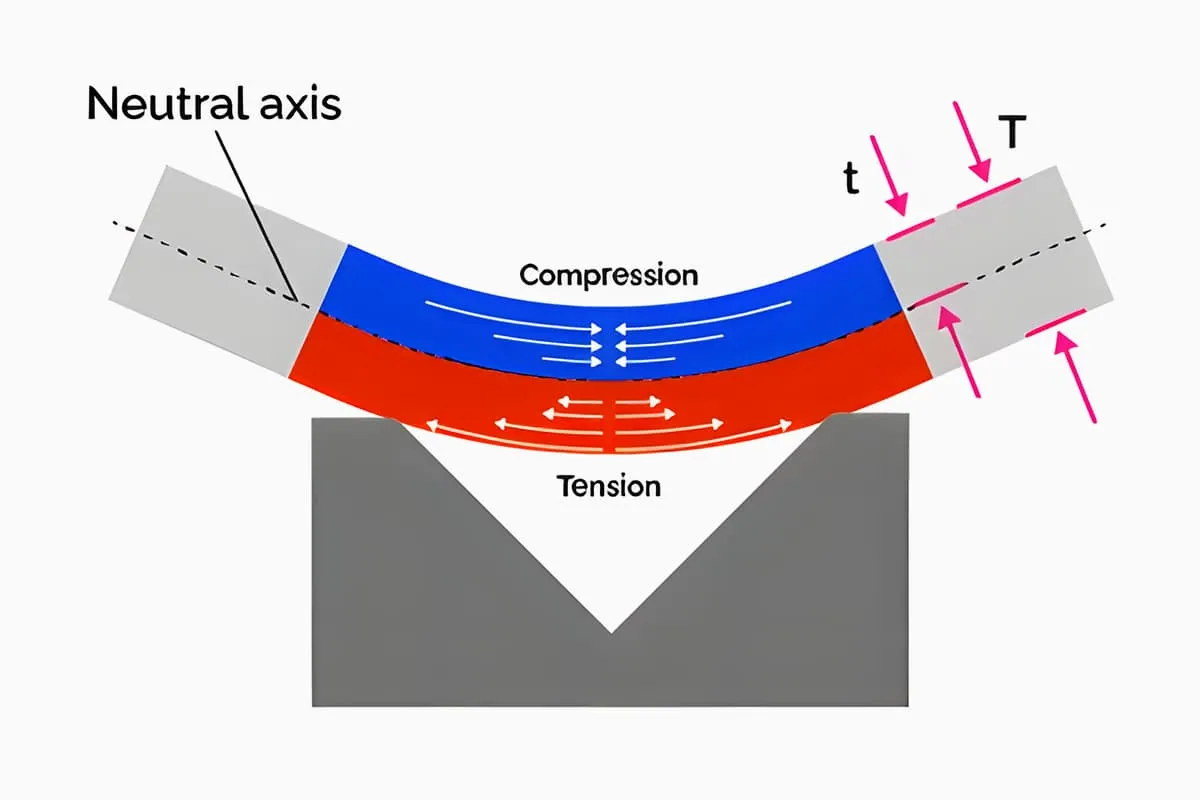
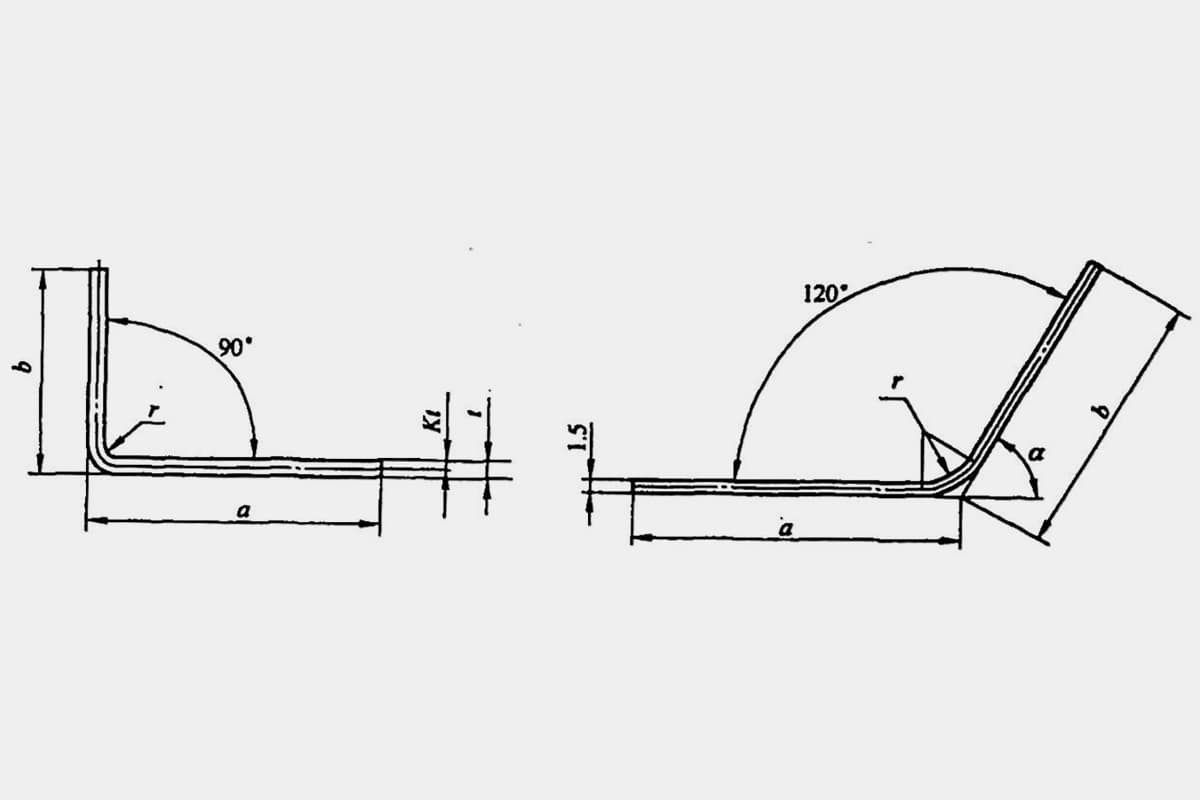
금속 재료의 이론적 무게 G를 계산하는 방법은 단면적 A에 길이 L을 곱한 다음 재료의 밀도 ρ을 곱하는 것입니다. 공식은 다음과 같습니다.
G=ALρ/1000
공식에서
- G - 금속 재료의 이론적 무게(kg)입니다;
- A - 금속 재료의 단면적 (mm2), 표 1은 다양한 강철 단면적에 대한 계산 공식을 제공합니다;
- L - 금속 재료의 길이(m)입니다;
- ρ - The 금속의 밀도 재료(g/cm3), 표 2는 일반적으로 사용되는 금속 재료의 밀도를 제공합니다.
표 1 강철 단면적 계산 공식
| 강철 이름 | 단면적 계산 공식 | 코드 설명 |
| 스퀘어 스틸 | A=a2 | a-사이드 너비 |
| 코너 스퀘어 스틸 | A=a2-0.8584r2 | a-사이드 너비; r-코너 반경 |
| 강판, 평강, 스트립 강판 | A=at | a-사이드 너비; t-두께 |
| 코너 플랫 스틸 | A=at-0.8584r2 | a-사이드 너비; t-두께; r-코너 반경 |
| 원형 강철, 원형 막대, 강선 | A=0.8584d2 | d-외경 |
| 육각 강철 | A=0.866초2=2.598a2 | 반대편 사이의 거리입니다; a-사이드 너비 |
| 팔각형 강철 | A=0.8284초2=4.8284a2 | |
| 강철 파이프 | A=3.1416δ(D-δ) | D-외경; Δ-벽 두께 |
| 등각 강철 | A=d(2b-d)+0.2146(r)2-2r12) | d- 가장자리 두께; b- 가장자리 너비; r-내부 모서리 반경; r1-끝 가장자리 반경 |
| 불균등 각도 강철 | A=d(B+b-d)+0.2146(r)2-2r12) | d- 가장자리 두께; b- 짧은 가장자리 너비; B-긴 가장자리 너비; r-내부 모서리 반경; r1-끝 가장자리 반경 |
| I-Beam | A=hd+2δ(b-d)+0.8584(r2-r12) | h-높이; b-다리 너비; d-허리 두께; Δ-평균 다리 두께; r-내부 모서리 반경; r1-끝 가장자리 반경 |
| 채널 스틸 | A=hd+2δ(b-d)+0.4292(r2-r12) |
표 2 일반적인 금속 재료의 밀도
| 재료 이름 | 밀도/(g/cm3) |
| 탄소강 | 7.85 |
| 주강 | 7.80 |
| 회색 주철 | 6.80～7.20 |
| 연성 철 | 7.20～7.40 |
| 경질 합금(텅스텐) | 13.90～14.90 |
| 고속 강철 | 8.30～8.70 |
| 순수 구리 | 8.90 |
| 황동 | 8.40～8.85 |
| 주석 청동 | 8.70～8.90 |
| 우시 브론즈 | 7.50～8.20 |
| 산업용 알루미늄 | 2.70 |
| 마그네슘 합금 | 0.74～1.81 |
| 실리콘 강판 | 7.55～7.80 |
| 주석 기반 베어링 합금 | 7.34～7.75 |
| 납 기반 베어링 합금 | 9.33～10.67 |
냉간 가공 제품 중 가장 널리 사용되고 가장 많은 양이 사용되는 재료는 강판입니다. 강판의 무게를 계산할 때 ρ는 7.85g/cm이므로 다음과 같이 계산합니다.3
에서 강판의 면적 A를 위의 공식에 대입하면 강판의 무게 G에 대한 계산식을 구할 수 있습니다:
G=7.85At
공식에서
- G - 강판의 이론적 무게(kg)입니다;
- A - 강판의 면적(m2);
- t - 강판의 두께(mm)입니다.
한국어 
English 
العربية 
Bahasa Indonesia 
Deutsch 
Español 
Français 
Italiano 
日本語 
Nederlands 
Português 
Português do Brasil 
Русский 
Polski 
Türkçe