판금 절곡 부품의 경우 블랭크 크기를 계산하는 것은 절곡 공정 계획을 수립하기 위한 전제 조건입니다. 기술자마다 공정 문서에서 서로 다른 벤딩 허용 계수를 선택할 수 있으며, 블랭크 크기의 정확성은 벤딩 부품의 치수 정확도와 제품 품질에 직접적인 영향을 미칩니다.
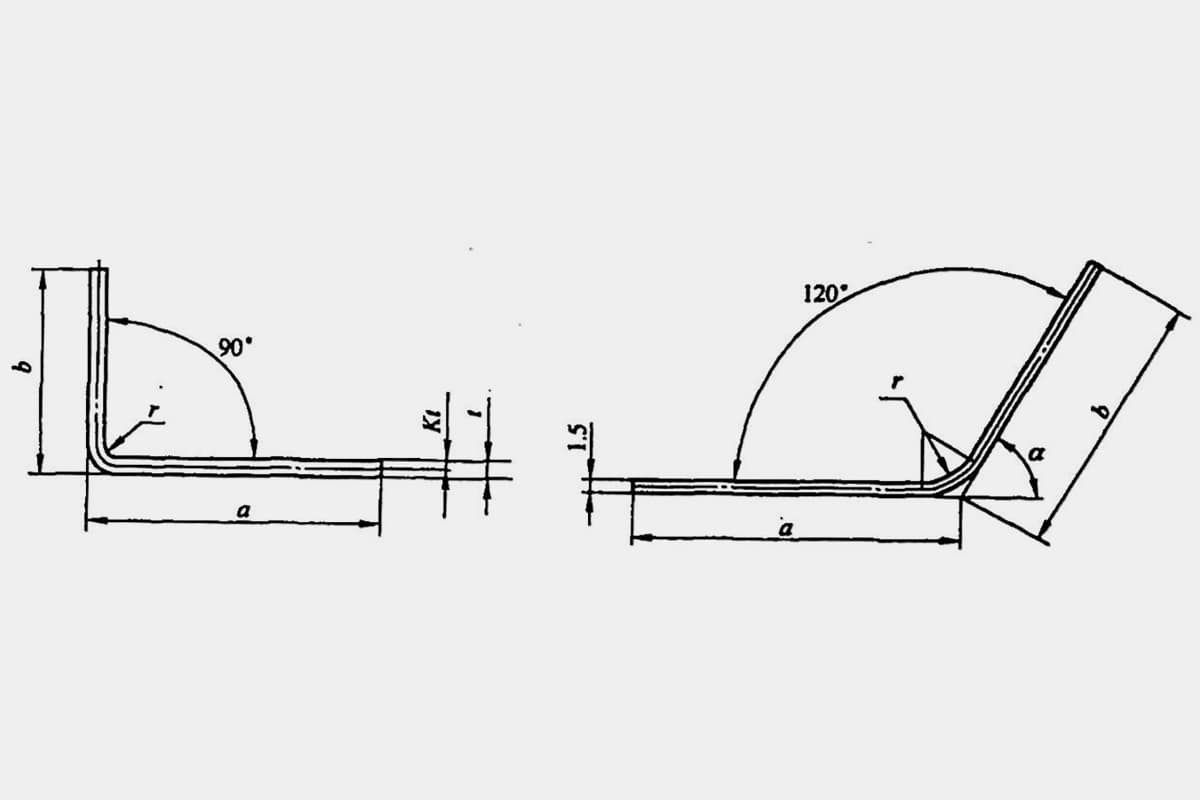
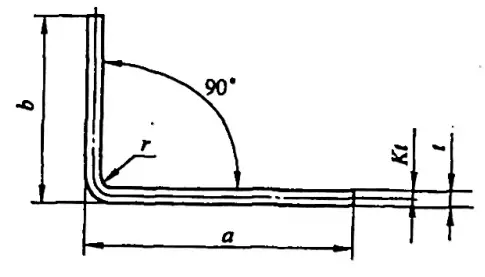
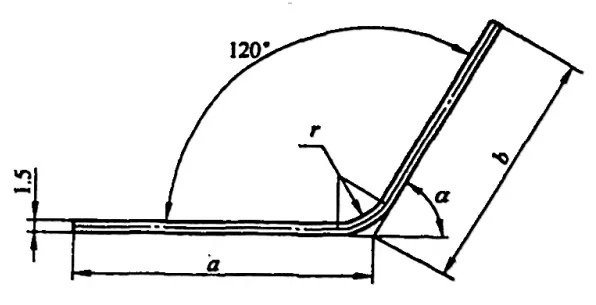
때로는 부정확한 계산으로 인해 낭비가 발생할 수도 있습니다. 일반적인 단순 굽힘 부품(그림 5-1 참조)의 펼쳐진 길이 L은 L = a + b - y입니다(여기서 y는 굽힘 공제이며 R 부분에 대한 보정 값이라고도 함).
그러나 다양한 매뉴얼과 자료에서 φ=90°에 대한 굽힘 공제는 직접 구할 수 있지만, 그림 5-2와 같이 90°가 아닌 굽힘의 경우 기술자는 경험 계수(K 계수)를 기반으로 계산해야 합니다.
관련 읽기: 판금 접기 기술 설명
1. 판금 굽힘의 펼쳐진 치수 계산 원리
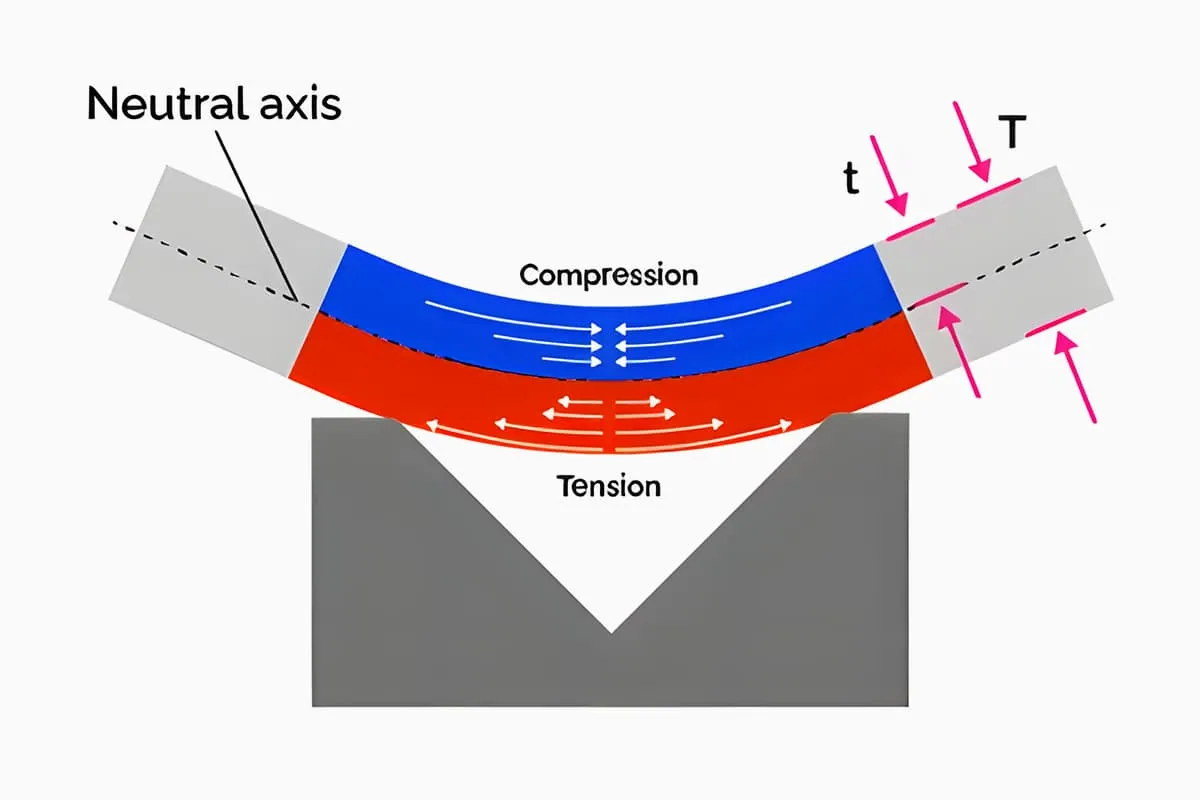
구부러진 블랭크의 펼쳐진 치수는 구부리기 전후에 중성층의 길이가 변하지 않는다는 원칙에 따라 결정됩니다. 판재가 구부러지면 블랭크 섹션의 외층 섬유는 늘어나고 내층 섬유는 압축됩니다.
외층 섬유의 신축성은 바깥쪽에서 안쪽으로 점차 감소하고 내층 섬유의 압축도 안쪽에서 바깥쪽으로 점차 감소합니다.
섬유가 연신에서 압축으로 또는 압축에서 연신으로 전환될 때 응력과 변형이 0이고 굽힘 전후에 길이가 변하지 않는 섬유 층이 있어야 합니다.
이 레이어를 중립 레이어라고 정의합니다. 따라서 구부러진 블랭크의 펼쳐진 치수를 계산하는 데 있어 핵심은 중성층의 위치를 결정하는 것입니다. 중성층의 위치는 소성 변형 전후에 구부러진 부분과 블랭크의 부피가 같다는 조건에 따라 결정됩니다.
2. 중성층의 곡률 반경 ρ 결정하기
이론적으로 구부러진 부분의 두께 방향에 따라 변형이 고르지 않기 때문에 중성층은 포물면이지만 계산을 위해 일반적으로 원호 표면으로 간주합니다. 굽힘 변형이 매우 작은 경우(r/t >6.5), 중성층은 대략 재료 두께의 중간, 즉 중성층의 곡률 반경으로 간주할 수 있습니다. ρ=r+t/2.
변형이 매우 큰 경우(r/t≤6.5), 그림 5-3과 같이 재료 두께가 얇아지고 단면 왜곡이 매우 커집니다.
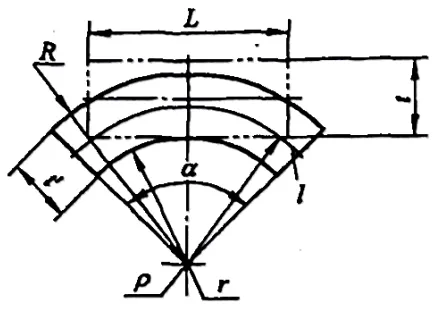
이때 단면 내 모든 작용력의 결과 힘이 0이라는 균형 조건을 만족시키기 위해서는 중성층이 재료의 안쪽 표면으로 이동해야 합니다.
이때 소성 변형 중 부피가 변하지 않는 조건, 즉 구부리기 전의 부피를 기준으로 중성층의 곡률 반경을 결정할 수 있습니다: V0=LBt, 구부린 후의 볼륨입니다:
V=(R2-r2) α*B'/2.
공식에서 B는 블랭크의 너비(mm), B'는 구부린 후 블랭크의 평균 너비(mm), α는 구부림 중심 각도입니다. 구부리기 전과 후의 부피가 같다는 원칙에 따라 V0=V입니다,
LBt=(R2-r2) α*B'/2, L=(R2-r2) α*B'/2tB(5-1).
중성층의 제로 응력과 변형률에서 L=l=αρ을 구할 수 있으며, 여기서 L은 중성층의 변형 전 길이(mm)이고, l은 중성층의 변형 후 길이(mm)입니다.
방정식 (5-1)을 대입하면 다음과 같습니다. ρ=(R2-r2) B'/2tB. 위의 방정식에 R=r+t'를 대입하면 다른 형태의 방정식을 얻을 수 있습니다. ρ=(r/t+η/2)tβη (5-2)여기서 β는 폭 계수, β=B'/B이며, 일반적으로 넓은 판(B>3t)을 구부릴 때 일반적으로 β=1, η는 얇아짐 계수, η=t'/t로 간주합니다.
방정식 (5-2)는 이론적으로 중성층의 위치를 계산하는 공식입니다. 계산할 때 η, 즉 희석 법칙을 알아야 합니다. η의 값은 표 5-1에서 참조할 수 있습니다.
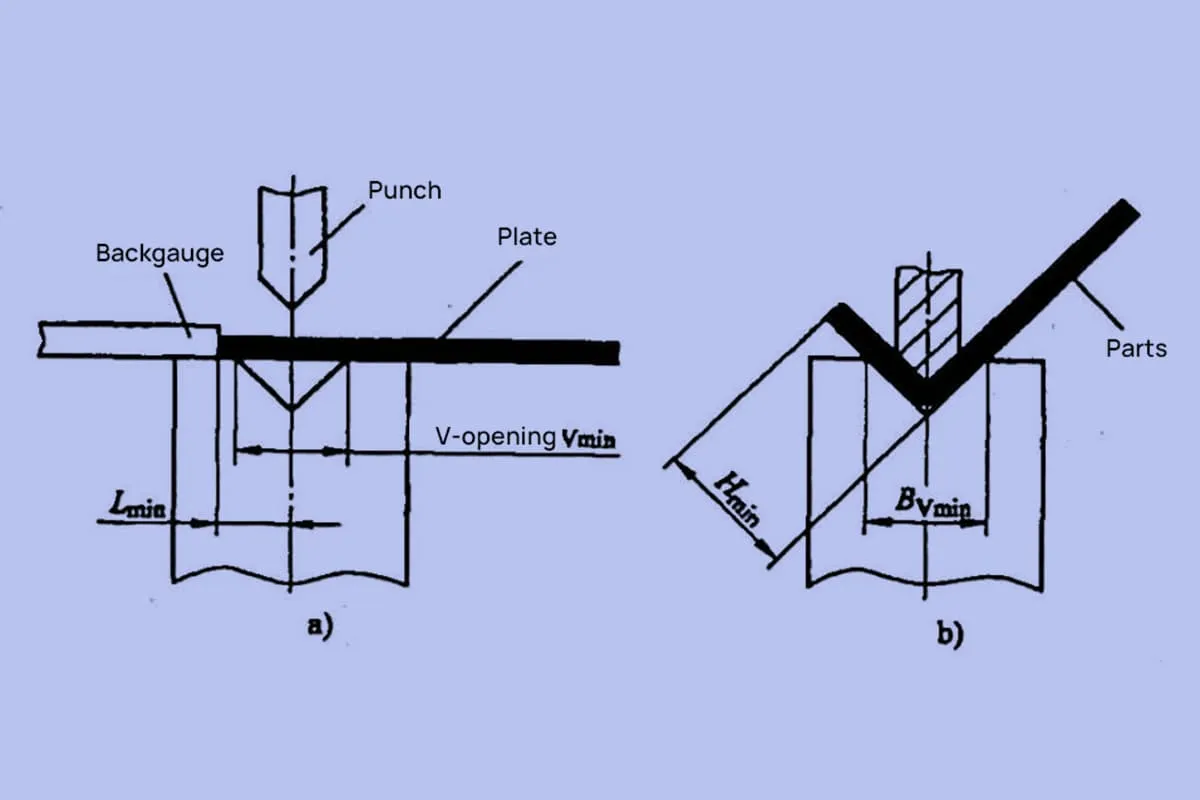
엷게하는 규칙은 매우 복잡하고 굽힘 영역에서 중성층의 위치 분포가 균일하지 않으며 엷게하는 규칙은 굽힘 방법, 굽힘 하단 다이 슬롯의 너비 및 재료 두께와 같은 많은 요소와 관련이 있다는 점을 지적해야합니다.
이로 인해 중성층 위치의 이론적 계산에 불가피한 오류가 발생하여 이론적 결정 방법의 실제 적용 가치가 감소합니다.
표 5-1: 얇아짐 계수 η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
실제 제작에서는 일반적으로 다음과 같이 이론적 계산보다 더 간단한 경험적 공식을 사용하여 중립축의 위치를 결정합니다:
ρ = r + Kt (5-3)
Where:
- ρ - 중립축의 곡률 반경(mm)
- r - 원재료의 내부 굽힘 반경(mm)
- t - 재료 두께(mm)
- K - 중립축 계수(경험적 K 팩터), 표 5-2를 참조하십시오.
표 5-2: 중립축 계수 K의 경험적 값
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
참고:
- K1 는 상판 또는 프레스 플레이트가 있는 V자형 또는 U자형 굴곡에 적용할 수 있습니다.
- K2 는 상판이 없는 V자형 굴곡에 적합합니다.
3. 여러 가지 일반적인 판금 굽힘에 대한 블랭크 펼쳐진 치수 계산 3.
중립 레이어의 정의에 따라 펼쳐진 빈 치수는 중립 레이어의 길이와 같아야 합니다. 일반적으로 내부 굽힘 반경 r의 값에 따라 굴곡은 둥근 모서리와 둥근 모서리가 아닌 굴곡으로 분류되며, r>0.5t인 경우 굴곡은 둥근 모서리로 간주되고 r<0.5t인 경우 둥근 모서리가 아닌 굴곡으로 간주됩니다.
또한, 굽힘은 판 폭 B에 따라 넓은 판 굽힘과 좁은 판 굽힘으로 분류되는데, 판 폭 B>3t일 경우 넓은 판 굽힘, 판 폭 B<3t일 경우 좁은 판 굽힘으로 구분합니다.
생산 실무에서는 둥근 모서리 반경(r>0.5t)과 넓은 판(B>3t)의 벤딩이 가장 널리 사용되며, 벤딩의 보편성을 고려하여 벤딩 시 둥근 모서리 반경과 넓은 판을 가진 벤딩의 빈 펼침 치수 계산에 대해 주로 논의합니다.
3.1 둥근 모서리 굴곡(r>0.5t)의 블랭크 펼쳐진 치수 계산
굽힘 부분의 얇아짐이 심하지 않고 단면 왜곡이 작기 때문에 r>0.5t, B>3t인 경우 중성층의 길이가 블랭크 펼쳐진 치수와 같다는 원칙에 따라 블랭크의 길이를 결정할 수 있습니다.
둥근 모서리 굽힘(r>0.5t)의 빈 펼쳐진 치수를 계산하는 일반적인 방법은 굽힘 계수 계산과 굽힘 공제 값 계산으로 나뉩니다.
1. 빈 펼친 치수에 대한 둥근 모서리 굽힘(r>0.5t) 굽힘 계수 계산:
1) 굽힘 계수는 그림 5-4와 같이 굽힘 변형 영역(굽힘 R 부분)의 중성층을 따라 측정한 아크 부분의 길이입니다.
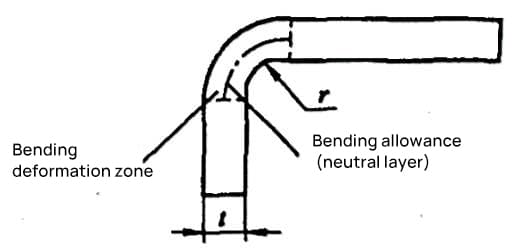
굽힘 계수는 공식 (5-4)에 의해 계산됩니다: x=παρ/180° (5-4)
여기서 ρ는 중성층의 곡률 반경(mm)입니다.
2) 그림 5-5는 빈 펼침 치수의 휨 계수 계산을 위한 치수 표기 예시이며, 빈 펼침 치수의 휨 계수 계산 공식은 다음과 같습니다.

a) φ > 90° b) φ≤90
L=a+b+x(5-5)
방정식 (5-3)을 방정식 (5-4)에 대입하면 굽힘 계수에 대한 공식을 구할 수 있습니다:
x=πα(r+Kt)/180°(5-6)
방정식 (5-6)을 방정식 (5-5)에 대입하면 구부러진 공백의 펼쳐진 크기를 계산하는 공식을 구할 수 있습니다:
L=a+b+πα(r+Kt)/180°(5-7)
Where:
- L - 블랭크의 펼쳐진 크기(mm)입니다;
- K - K 계수, 해당 값은 표 5-2를 참조하세요;
- α - 굽힘의 중심 각도, 구부러진 부분의 각도와의 관계는 α=180°-φ입니다;
- r - 블랭크 내부 레이어의 굽힘 반경(mm)입니다;
- t - 소재의 두께(mm)입니다;
- a, b - 각각 구성 요소의 직선 부분의 길이(mm)입니다.
2. 둥근 모서리 구부러진 부분의 펼쳐진 크기에 대한 굽힘 공제 계산(R>0.5T)
1) 굽힘 공제(R 부분에 대한 보정 값이라고도 함)는 그림 5-6과 같이 굽힘 변형 영역(굽힘의 R 부분)의 R과 굽힘 계수의 두 배의 차이로, 굽힘 공제는 굽힘 계수라고도 합니다.

굽힘 공제(R 부분에 대한 보정 값)는 공식 (5-8)에 따라 계산됩니다:
y = 2R-παr/180°(5-8)
2) 그림 5-7은 블랭크의 펼쳐진 크기에 대한 굽힘 공제 계산을 위한 치수 주석의 예를 보여줍니다. 굽힘 공제 Y는 다음 공식으로 계산됩니다:
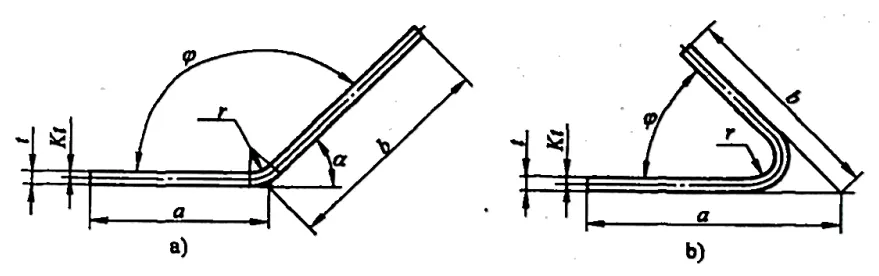
A)90°<φ≤165° B)φ≤90°
φ ≤ 90°인 경우:
R=(r+t)/탄(φ/2)
위의 공식과 공식 (5-3)을 공식 (5-8)에 대입하면 φ≤90° 굽힘에 대한 굽힘 공제(즉, R 부분의 보정 값)를 구할 수 있습니다(그림 5-7b 참조):
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
90°<φ≤165°인 경우:
R=(r+t)tan[(180°-φ)/2]
위의 공식과 공식 (5-3)을 공식 (5-8)에 대입하면 90°<φ≤165° 굽힘에 대한 굽힘 공제(즉, R 부분의 보정 값)를 구할 수 있습니다(그림 5-7a 참조):
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
165°<φ≤180°인 경우:
y≈0
3) 그림 5-7에 표시된 부품의 블랭크 사이즈의 휨 공제값을 계산하는 공식은 다음과 같습니다:
L=a+b-y(5-11)
φ≤90°일 때 식 (5-9)를 식 (5-11)에 대입하면 다음과 같이 블랭크 사이즈의 휨 공제값을 계산하는 공식을 구할 수 있습니다:
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
90°<φ≤165°일 때 식 (5-10)을 식 (5-11)에 대입하면 다음과 같이 블랭크 사이즈의 휨 공제값을 계산하는 공식을 구할 수 있습니다:
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
165°<φ≤180°인 경우:
L≈a+b(5-14)
Where,
- Y - 굽힘 공제(mm)
- L - 부품의 블랭크 크기(mm)
- r - 블랭크의 내부 굽힘 반경(mm)
- t - 재료 두께(mm)
- α - 굽힘 중심 각도, 굽힘 각도와의 관계는 α=180°-φ입니다.
- a, b - 구부러지는 버텍스까지 부품의 가장자리 길이(mm)입니다.
3. 다각도 굴곡을 위한 블랭크 크기 계산
다중 각도 벤드의 경우 빈 크기는 R 부분과 직선 가장자리의 길이를 합한 값입니다.
1) 굽힘 계수에 의한 다각도 굽힘 블랭크 크기 계산:
L=l1+l2+...+ln+1+nx (5-15)
여기서 l1, l2...ln+1 는 부품의 각 가장자리 직선 부분의 길이(mm)입니다;
n은 벤드 R의 수입니다.
2) 굽힘 공제에 의한 다중 각도 굽힘 블랭크 크기 계산:
L=l1+l2+...+ln+1-ny (5-16)
여기서 l1, l2...ln+1 는 부품의 가장자리에서 굽힘 꼭지점까지의 길이(mm)입니다;
n은 벤드 R의 수입니다.
예 5-1: 그림 5-8에 표시된 굴곡의 빈 크기를 계산합니다.
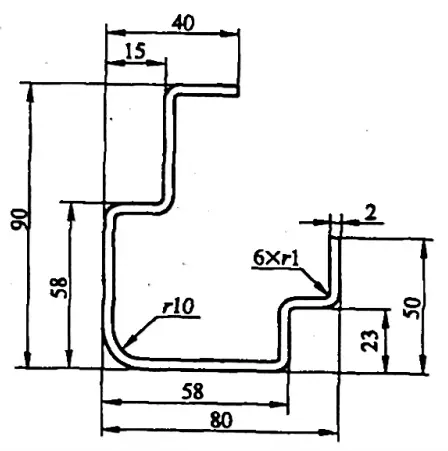
해결 방법 1: 굽힘 계수를 사용하여 빈칸 크기를 계산합니다.
부록 A 참조: 굽힘 조각 각도 φ=90°, 두께 t=2mm, 반경 r=10mm일 때 굽힘 계수는 2.68mm입니다;
굽힘 조각 각도가 90°, 두께 t=2mm, 반경 r=10mm인 경우 굽힘 계수는 x2=16.9mm입니다.
방정식 (5-5) 및 (5-15)에서 구부러진 조각에 대한 블랭크의 평평한 크기는 다음과 같이 계산됩니다:
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2.68 + 16.9]mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240.98mm.
해결 방법 2: 굽힘 공제 값을 사용하여 블랭크의 평평한 크기를 계산합니다.
부록 C 참조: 각도 φ=90°, 두께 t=2mm, 반경 r=1mm의 굽힘의 경우 R 섹션의 보정 값은 y1=3.32mm이고 각도 φ=90°, 두께 t=2mm, 반경 r=10mm의 굽힘의 경우 R 섹션의 보정 값은 y2=7.1mm입니다.
구부러진 부분의 원시 크기는 방정식 (5-11) 및 (5-16)에서 얻을 수 있습니다:
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3.32 - 7.1] mm
= (25+34+17+116+25+24+27-19.92-7.1) mm
= 240.98 mm
예 5-2: 그림 5-9에 표시된 구부러진 부분의 원시 크기를 계산합니다.
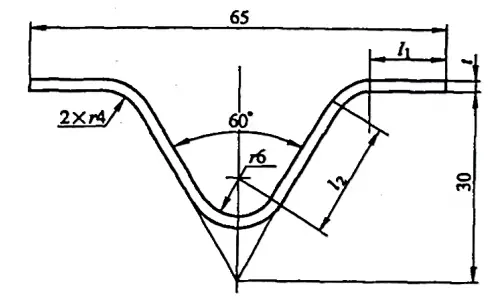
솔루션: 굽힘 계수를 사용하여 원시 크기를 계산합니다.
방정식 (5-5) 및 (5-15)에서 구부러진 부분의 빈 치수를 계산하는 공식은 다음과 같습니다:
L=2l1+2l2+2x1+x2
여기서 l1 = [32.5 - (30tan30°+4tan30°)] mm = 12.87 mm
및 l2 = [(30/cos30°) - (8/tan30°+4tan30°)] mm = 18.47 mm
부록 A 참조: 굽힘 각도 φ=120°, t=2mm, r=4mm인 경우 굽힘 계수 값은 x입니다.1=4.98mm; 굽힘 각도 φ=60°, t=2mm, r=6mm일 때 굽힘 계수 값은 x입니다.2=14.16mm.
이 값을 공식에 대입하면 빈 펼친 길이는 L= (2×12.87 + 2×18.47 + 2×4.98 + 14.16) mm = 86.8mm가 됩니다.
정밀도 요구 사항이 낮은 간단한 벤드의 경우 블랭크의 펼쳐진 치수를 직접 계산할 수 있다는 점에 유의하세요. 그러나 더 복잡한 벤드 또는 더 높은 정밀도 요구 사항이 있는 벤드의 경우, 펼쳐진 블랭크의 모양과 치수를 반복적으로 테스트하고 지속적으로 수정하여 블랭크의 모양과 치수를 확인해야 합니다.
3.2 샤프 벤드 컴포넌트의 블랭크 개발 치수 계산(r<0.5t)
구성 요소의 굽힘 반경 r이 0.5t 미만인 경우 이를 날카로운 굽힘이라고 합니다. 이러한 컴포넌트에 대한 블랭크 개발 치수의 계산은 굽힘 전후의 부피 일관성 원칙을 기반으로 합니다.
급격한 굽힘의 경우 굽힘 부위의 재료가 심하게 얇아지기 때문에 변형 과정이 매우 복잡하여 블랭크 개발 치수를 정확하게 계산하기 어렵습니다. 따라서 계산된 블랭크 개발 치수는 경험적 데이터를 기반으로 또는 시험 굽힘을 통해 보정해야 합니다.
날카로운 굽힘 구성 요소(r<0.5t, φ=90°)의 블랭크 개발 치수에 대한 계산 공식은 표 5-3에서 확인할 수 있습니다.
표 5-3 날카로운 굴곡 부품(r<0.5t, φ=90°)의 블랭크 개발 치수 계산 공식(단위: mm)
| 일련 번호 | 벤딩 기능 | 도식 | 공식 |
| 1 | 모서리를 구부립니다. |  | L=a+b+0.4t |
| 2 | 평평하게 만듭니다. |  | L=a+b-0.43t |
| 3 | 한 번에 두 모서리를 구부립니다. | 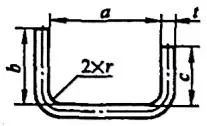 | L=a+b+c+0.6t |
| 4 | 세 모서리를 동시에 구부립니다. | 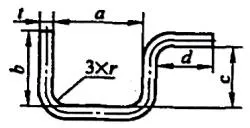 | L=a+b+c+d+0.75t |
| 5 | 첫 번째 모서리 두 개를 구부리고 두 번째 모서리를 구부린 다음 다른 모서리를 구부립니다. | L=a+b+c+d+t | |
| 6 | 네 모서리를 동시에 구부립니다. | 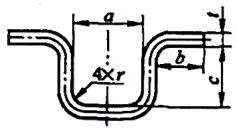 | L=a+2b+2c+1.2t |
| 7 | 구부려서 두 번에 걸쳐 네 모서리를 만듭니다. | L=a+2b+2c+1.2t |
3.3 힌지형 벤딩 파트의 펼쳐진 치수 계산
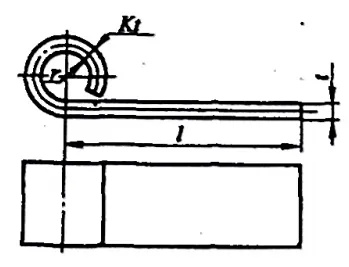
힌지형 굽힘 부품 r= (0.6~3.5)t(그림 5-10 참조)인 경우, 플랜지 공정은 일반적으로 그림 5-11에 표시된 패턴을 따릅니다. 플랜징하는 동안 판금의 두께가 증가하고 중성층이 바깥쪽으로 이동합니다. 블랭크의 펼쳐진 치수는 다음 공식으로 대략적으로 계산할 수 있습니다:
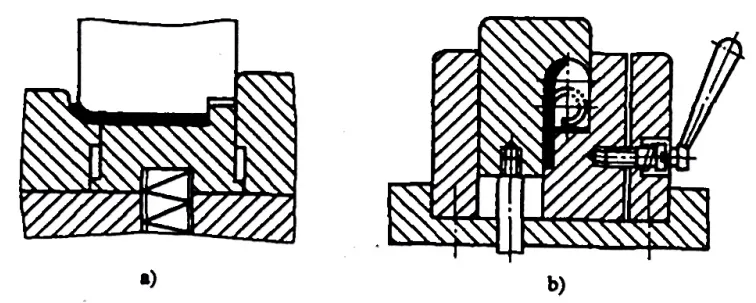
- a) 첫 번째 작업
- b) 두 번째 작업
L=l+1.57π(r+Kt)+r
Where:
- L - 블랭크의 펼친 치수(mm)입니다;
- l - 직선 세그먼트의 길이(mm)입니다;
- r - 블랭크의 내부 굽힘 반경(mm);
- K - 중성층의 변위 계수. r/t = 0.5~1.8인 경우 K는 일반적으로 0.5~0.70으로 간주합니다(r/t 값이 작을수록 K 값이 커지고, 반대로 작을수록 K 값이 작아집니다). 표 5-4에 따라 선택할 수도 있습니다.
표 5-4 힌지형 굽힘 부품의 중성층 변위 계수
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |