판금 부품 개발 도면을 작성하는 과정에서 가공 재료 두께의 영향, 즉 적절한 판재 두께 조정도 고려해야 합니다.
일반적으로 두께가 3mm 미만인 시트 소재의 경우 판재 두께 조정이 필요하지 않습니다. 시트 재료의 중심 직경 또는 내부 및 외부 표면 절단선에 따라 계산할 수 있습니다. 성형 후 치수는 허용 편차 범위 내에 있습니다. 판재 두께가 3mm보다 큰 경우 판재의 중심 직경에 따라 계산해야 합니다. 설명의 편의를 위해 다음 개발 재료에 대한 계산은 시트 재료의 중심 직경을 기준으로 합니다.
1. 원통형 쉘의 개발 계산
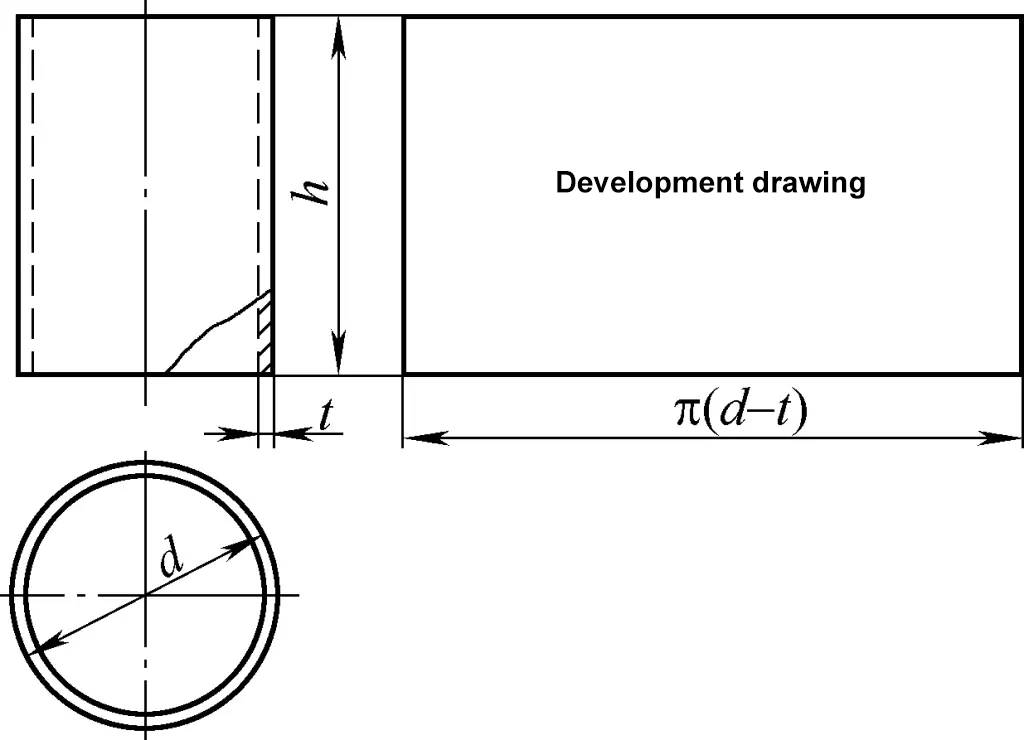
원통형 쉘은 원통형 표면에 속하며 개발 도면은 직사각형입니다. 직사각형의 한 변은 그림 1과 같이 원통의 둘레 π(d-t)와 같고 다른 한 변은 원통의 높이 h입니다. 그림에서 d는 원통의 외경이고 t는 판 두께입니다.
2. 오른쪽 원형 콘의 개발 계산
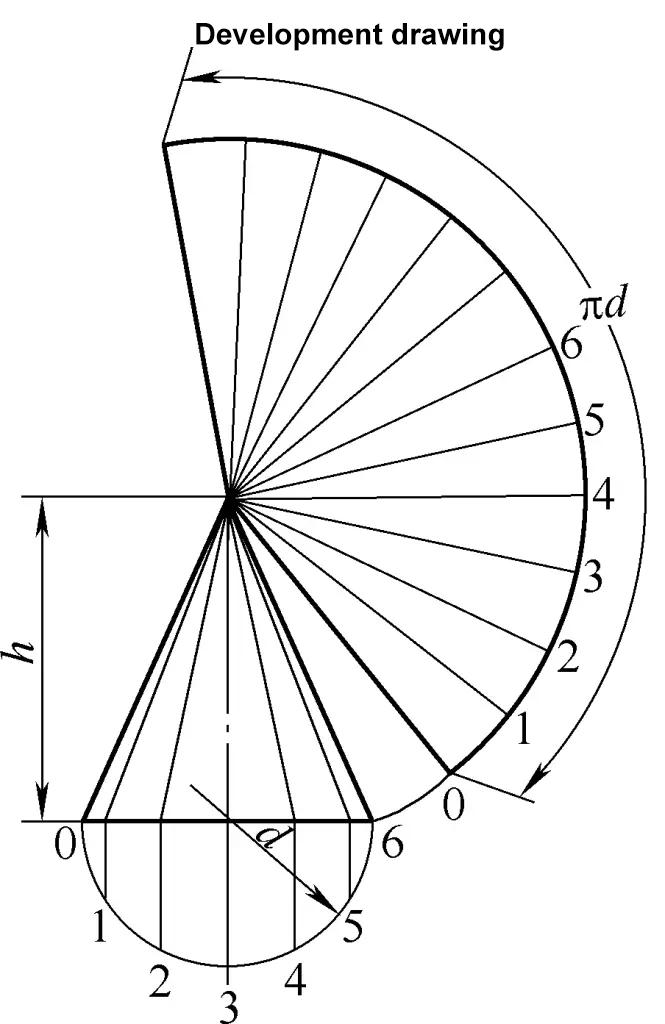
오른쪽 원형 원뿔의 전개도는 섹터 호입니다. 그림 2에 표시된 오른쪽 원뿔의 전개도 계산 공식은 다음과 같습니다:
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
공식에서
- R - 섹터 호의 반경(mm)입니다;
- α - 섹터 각도(°);
- L - 섹터 아크의 코드 길이(mm)입니다.
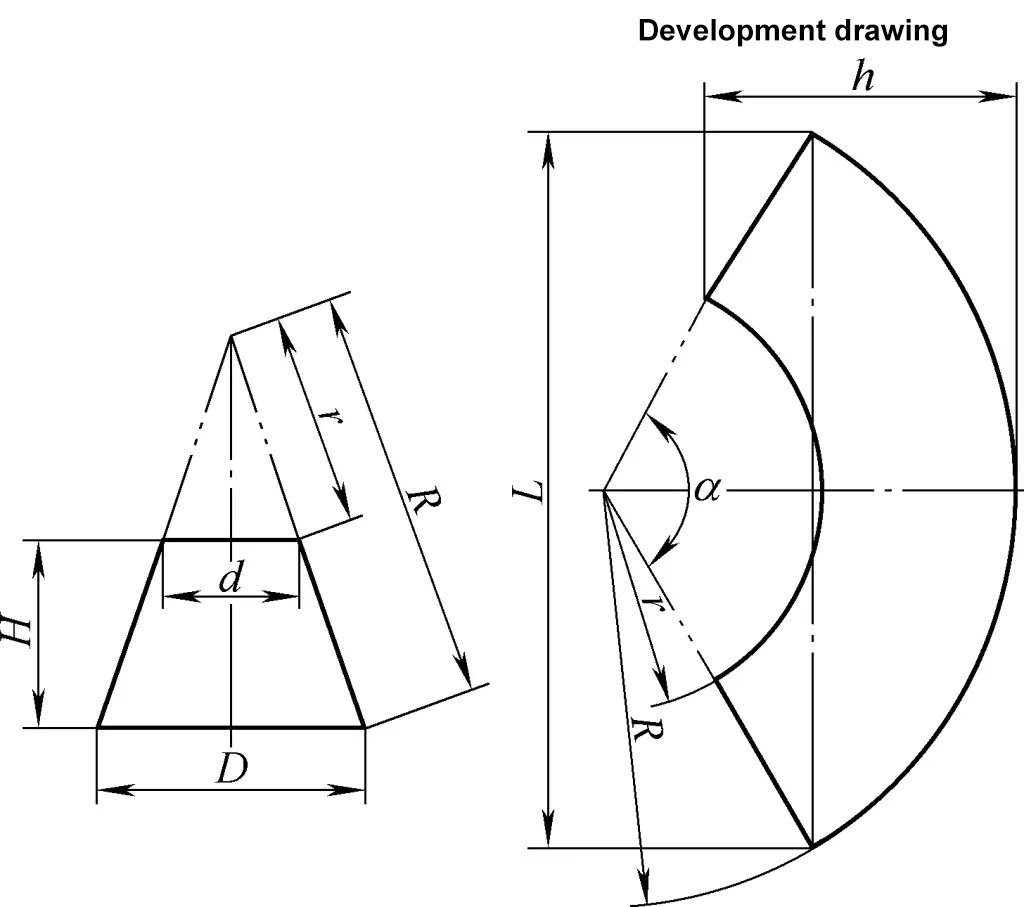
3. 잘린 오른쪽 원형 원뿔의 개발 계산
잘린 오른쪽 원뿔의 전개도는 동심 섹터 호입니다. 그림 3에 표시된 잘린 오른쪽 원뿔의 전개도 계산 공식은 다음과 같습니다:
R=√{(D/2)2+[DH/(D-d)]2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
α>180°일 때, h=R+rsin[(α-180)/2]
공식에서 기호의 의미는 그림 3을 참조하세요.
4. 비스듬한 오른쪽 원형 원뿔의 개발 계산
비스듬한 오른쪽 원형 원뿔의 전개도는 불규칙한 섹터 호입니다. 그림 4에 표시된 비스듬한 오른쪽 원형 원뿔의 전개도 계산 공식은 다음과 같습니다:
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[(A-D/2cosαn)2+(D/2)2죄2αn+H2]
yn=fn(1시간/H)
m=Dsin(180°/n )
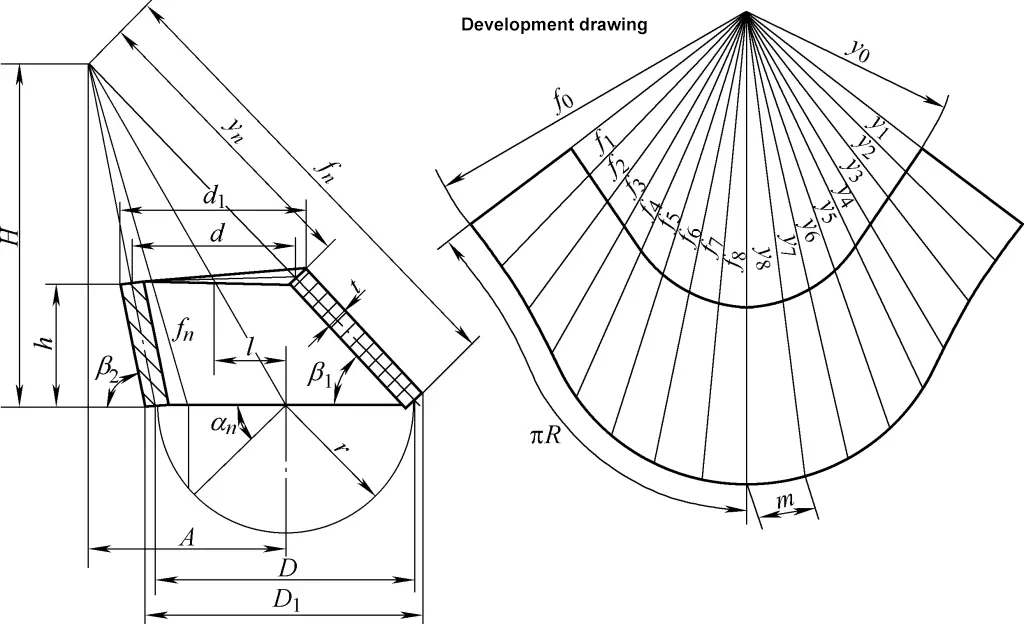
공식에서
- D1, d1 - 큰 끝과 작은 끝의 외경(mm)입니다;
- D, d - 큰 끝과 작은 끝의 중심 지름(mm)입니다;
- h - 중앙 높이(mm);
- l - 편심 거리(mm);
- n - 원주 주위의 분할 수; 분할 수가 많을수록 계산이 복잡해지지만 그림이 더 정확해집니다. 일반적으로 분할 수는 표 1에서 참조할 수 있습니다;
- fn, yn - 비스듬한 오른쪽 원형 원뿔의 경사선 길이(mm)입니다.
표 1 판금 개발을 위한 부서 수
| 개발된 조각의 반경/mm | 부서 수 |
| 50% 이내 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| 2000 이상 | 96 |
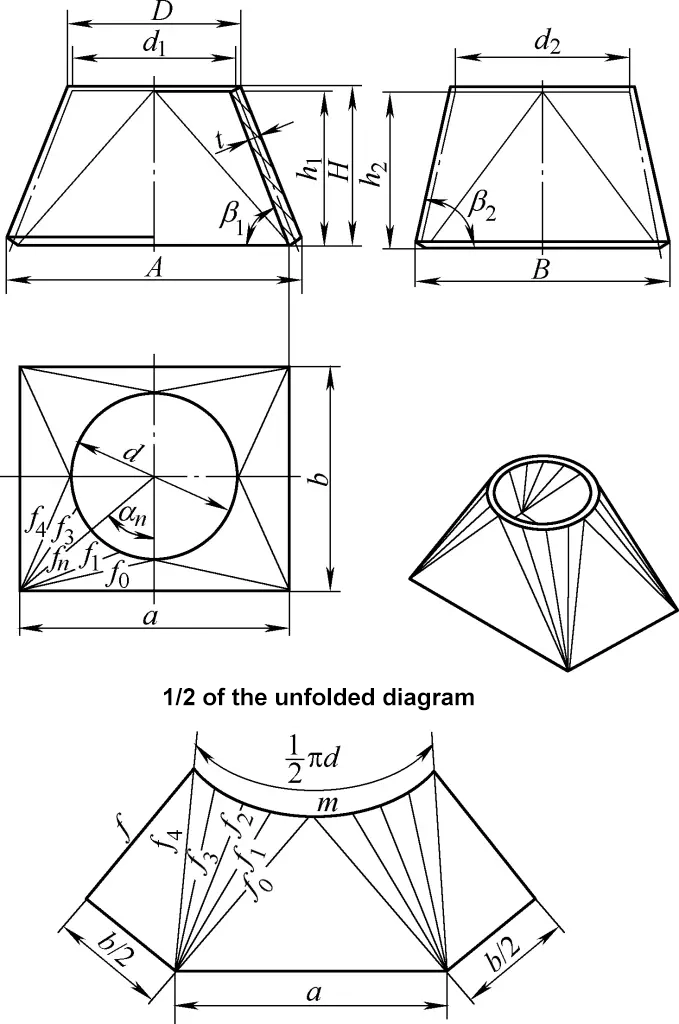
5. 직사각형에서 원형으로 전환하는 직사각형 전환 덕트의 개발 계산
그림 5에 표시된 직교 직사각형에서 원형 전환 덕트는 4개의 동일한 비스듬한 오른쪽 원형 원추형 표면과 4개의 대칭 삼각형 평면으로 구성됩니다. 개발 도면의 계산 공식은 다음과 같습니다:
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(0<α<90°일 때)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(α=90°일 때)
f=1/2√[(a-d)2+4h12]
m=πd/n
공식에서 기호의 의미는 그림 5를 참조하고, n은 원주 주위의 분할 수를 나타냅니다. 일반적으로 표 1의 나눗셈 개수는 계산 요구 사항을 충족할 수 있습니다.