Tijdens het maken van de ontwikkelingstekening van het plaatwerkonderdeel moet ook rekening worden gehouden met de invloed van de dikte van het verwerkingsmateriaal, dat wil zeggen dat de plaatdikte moet worden aangepast.
Over het algemeen is voor plaatmateriaal met een dikte van minder dan 3 mm geen aanpassing van de plaatdikte nodig. Deze kan worden berekend aan de hand van de centrale diameter van het plaatmateriaal of aan de hand van de snijlijnen aan de binnen- en buitenzijde. De afmetingen na het vormen vallen binnen het toelaatbare afwijkingsbereik. Als de plaatdikte groter is dan 3 mm, moet deze berekend worden aan de hand van de centrale diameter van het plaatmateriaal. Gemakshalve verwijzen de berekeningen voor de volgende ontwikkelde materialen naar de centrale diameter van het plaatmateriaal.
1. Ontwikkelingsberekening van cilindrische schalen
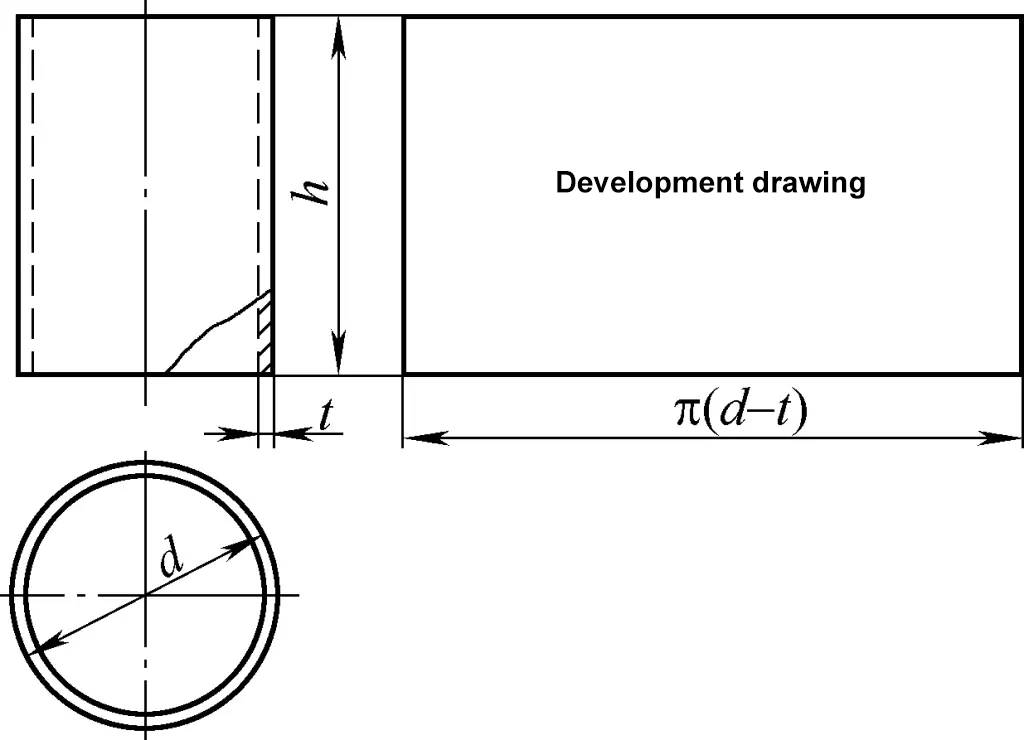
De cilindrische schil behoort tot het cilindrische oppervlak en de ontwikkelingstekening ervan is een rechthoek. Eén zijde van de rechthoek is gelijk aan de omtrek van de cilinder π(d-t), en de andere zijde is de hoogte h van de cilinder, zoals weergegeven in figuur 1. In de figuur is d de buitendiameter van de cilinder en t de plaatdikte.
2. Ontwikkeling Berekening van rechthoekige kegels
De ontwikkelingstekening van de rechter cirkelkegel is een sectorboog. De berekeningsformule voor de ontwikkelingstekening van de rechter cirkelkegel in figuur 2 is:
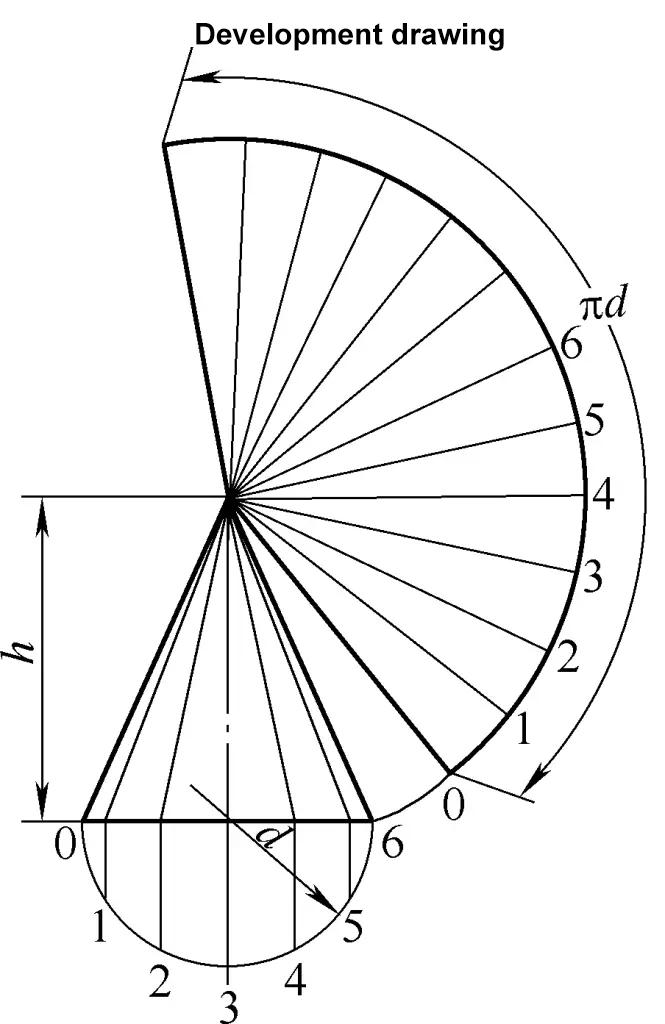
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
In de formule
- R - Straal van de sectorboog (mm);
- α - Sectorhoek (°);
- L - koordlengte van de sectorboog (mm).
3. Ontwikkelingsberekening van afgeknotte rechthoekige kegels
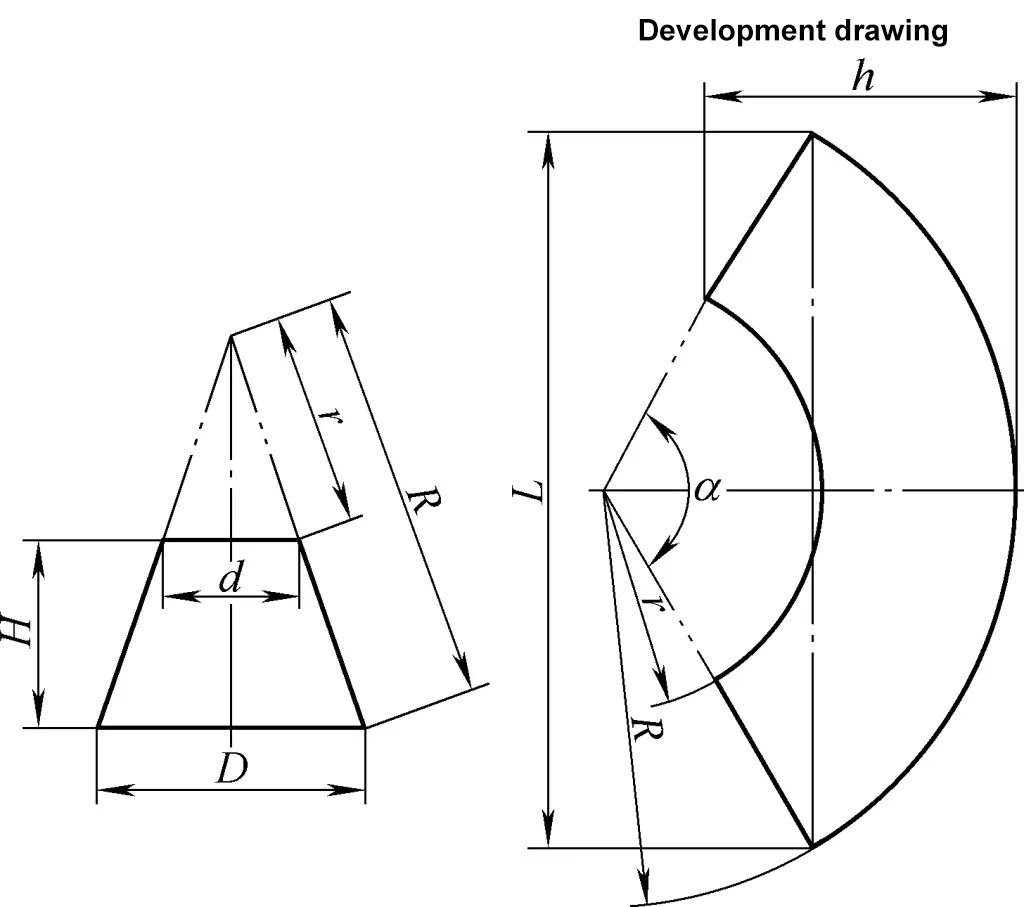
De ontwikkelingstekening van de afgeknotte rechte cirkelkegel is een concentrische sectorboog. De berekeningsformule voor de ontwikkelingstekening van de afgeknotte rechte cirkelkegel in figuur 3 is:
R=√{(D/2)2+[DH/(D-d)]2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
Wanneer α>180°, h=R+rsin[(α-180)/2]
Raadpleeg Figuur 3 voor de betekenis van de symbolen in de formule.
4. Ontwikkeling Berekening van schuine rechthoekige kegels
De ontwikkelingstekening van de schuine rechtse cirkelkegel is een onregelmatige sectorboog. De berekeningsformule voor de ontwikkelingstekening van de schuine rechtse cirkelkegel in figuur 4 is:
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[(A-D/2cosαn)2+(D/2)2zonde2αn+H2]
yn=fn(1-h/H)
m=Dsin(180°/n )
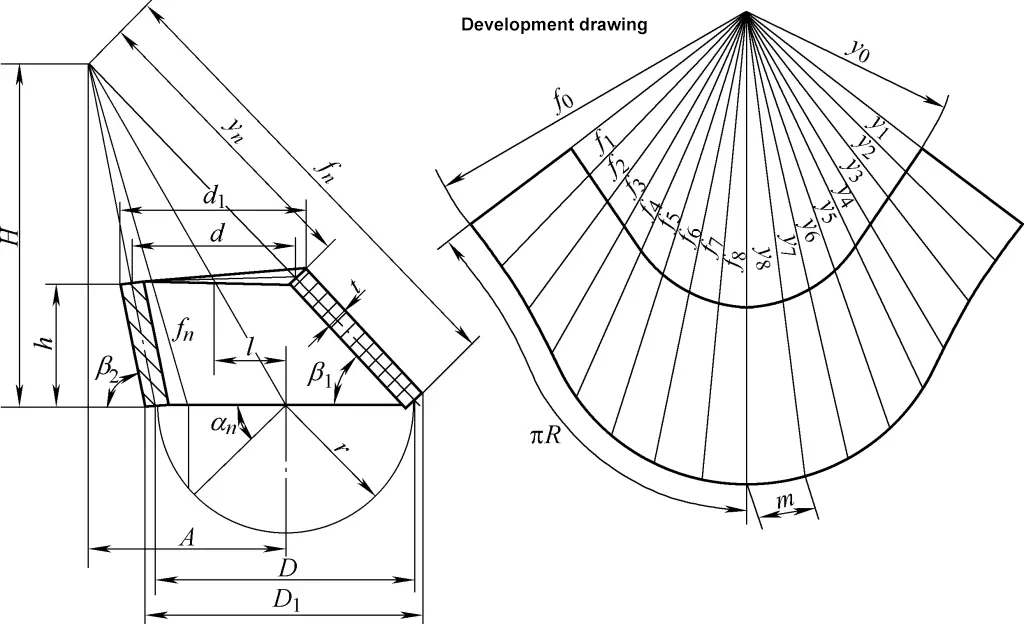
In de formule
- D1, d1 - Buitendiameter van de grote en kleine uiteinden (mm);
- D, d - Centrale diameters van de grote en kleine uiteinden (mm);
- h - centrale hoogte (mm);
- l - Excentrische afstand (mm);
- n - Aantal verdelingen rond de omtrek; hoe hoger het aantal verdelingen, hoe complexer de berekening maar hoe nauwkeuriger de tekening. Over het algemeen kan het aantal verdelingen worden weergegeven in tabel 1;
- fn, yn - Lengtes van de schuine lijnen van de schuine rechte cirkelkegel (mm).
Tabel 1 Aantal divisies voor plaatwerkontwikkelingen
| Straal van Ontwikkeld Stuk/mm | Aantal divisies |
| Binnen 50 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| Meer dan 2000 | 96 |
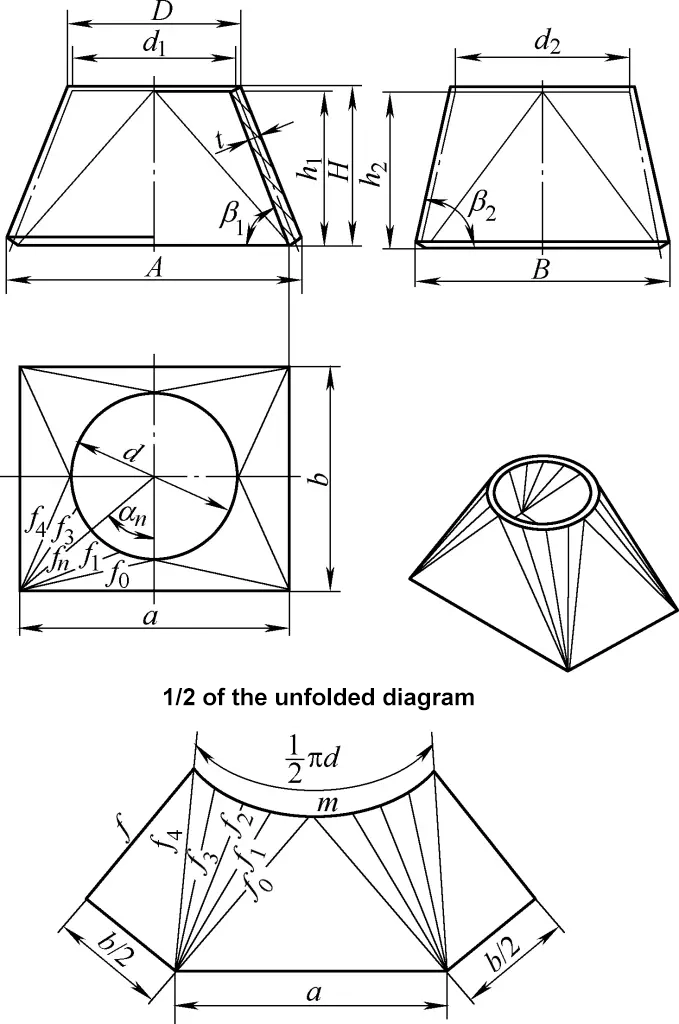
5. Ontwikkelingsberekening van de orthokonische rechthoekige naar ronde overgangskoker
De orthokonische rechthoekige naar ronde overgangskoker getoond in Figuur 5 bestaat uit vier gelijke schuine rechthoekige conische vlakken en vier symmetrische driehoekige vlakken. De berekeningsformule voor de ontwikkelingstekening is:
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(wanneer 0<α<90°)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(wanneer α=90°)
f=1/2√[(a-d)2+4h12]
m=πd/n
Zie figuur 5 voor de betekenis van de symbolen in de formule, en n is het aantal verdelingen rond de omtrek. Over het algemeen kan het aantal verdelingen in tabel 1 voldoen aan de berekeningsvereisten.