1. Sprężystość gięcia
Jak każda forma odkształcenia plastycznego, zginaniu rur towarzyszy odkształcenie sprężyste. Po usunięciu obciążenia, włókna po zewnętrznej stronie zginanej warstwy neutralnej skracają się z powodu sprężystego powrotu, a włókna po wewnętrznej stronie wydłużają się, zmieniając w ten sposób szybkość zginania i kąt zginania. Zjawisko to znane jest jako sprężynowanie. Istnieją dwie formy sprężynowania, jak pokazano na rysunku 4-25.
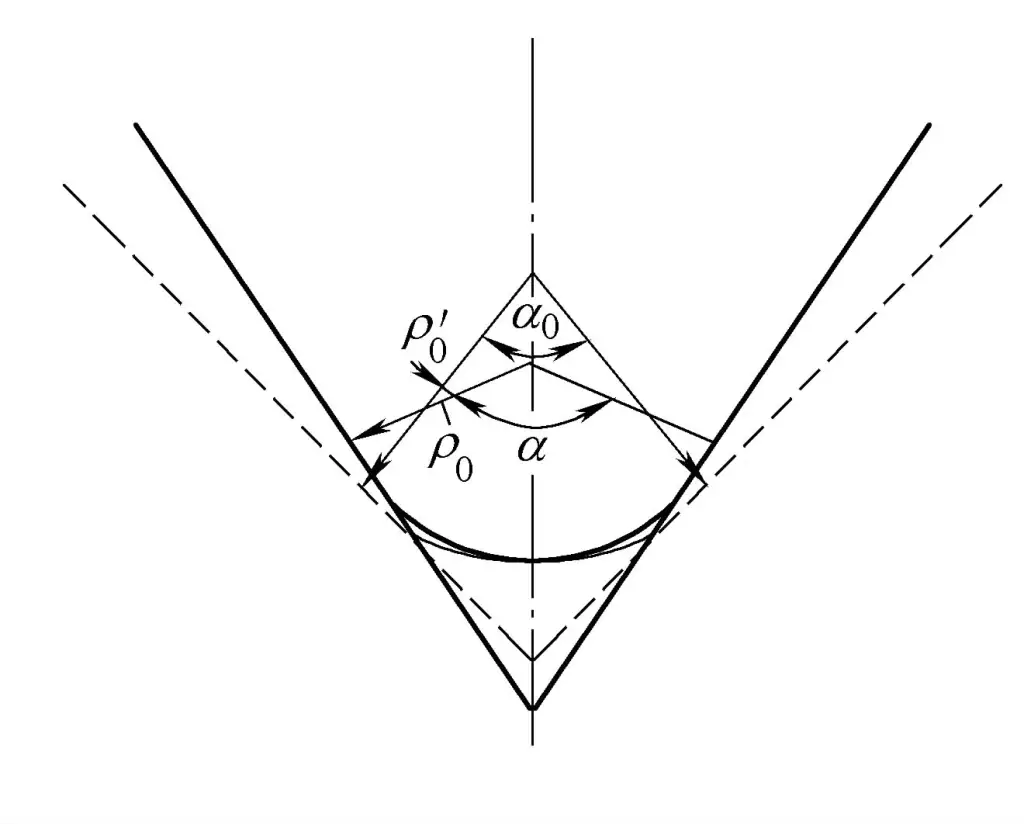
1) Krzywizna zmniejsza się.
Krzywizna zmniejsza się z 1/ρ0 przed rozładowaniem do 1/ρ'0 po rozładunku.
2) Kąt gięcia zmniejsza się.
Kąt zgięcia zmniejsza się z α przed rozładowaniem do α 0 po rozładowaniu. Wielkość sprężynowania można obliczyć na podstawie zmiany krzywizny ΔK lub zmiany kąta zgięcia Δα (zwanego również kątem sprężynowania).
Δα = α - α 0
(1) Czynniki wpływające na sprężynowanie przy zginaniu
W procesie gięcia istnieje wiele czynników wpływających na wielkość sprężynowania, główne czynniki są następujące:
1) Właściwości mechaniczne półfabrykatu.
Im mniejsza wartość σs /E, czyli im mniejsze σs a im większa wartość E, tym mniejsza wartość sprężynowania Δα.
2) Stopień odkształcenia r/t.
W tych samych warunkach, im mniejsza wartość r/t, tym większy stopień odkształcenia zginającego, udział odkształcenia sprężystego w całkowitym odkształceniu maleje, a więc zmniejsza się sprężystość zginania.
3) Centralny kąt gięcia α.
Im większy kąt centralny zginania α, tym większa długość strefy odkształcenia. W tych samych warunkach odkształcenia zmniejsza się wielkość odkształcenia na jednostkę długości. Dlatego im większy kąt zginania α, udział odkształcenia sprężystego w całkowitym odkształceniu odpowiednio wzrośnie, a wartość sprężynowania Δa będzie większa.
4) Prześwit matrycy Z.
Większy prześwit matrycywiększe sprężynowanie.
5) Metoda gięcia.
Wielkość sprężynowania jest niewielka w procesie gięcia ciągnionego, a najmniejsza w procesie gięcia pchanego.
6) Kształt przedmiotu obrabianego i stan struktury materiału.
Złożone kształty, wielokrotne wzajemne przyciąganie powodują małe sprężynowanie, duże sprężynowanie po hartowaniu na zimno.
7) Struktura formy i wielkość siły nacisku.
Siła docisku krawędzi jest duża, co skutkuje niewielkim odbiciem po wygięciu przedmiotu obrabianego.
(2) Określenie wartości odbicia
Określenie wartości odbicia przedmiotu obrabianego ma na celu podjęcie odpowiednich środków w celu przezwyciężenia odbicia, tak aby wygięty przedmiot obrabiany mógł spełnić wymagania dotyczące dokładności wzorca projektowego. Metody określania wartości odbicia obejmują metodę tabeli odnośników, metodę tabeli odnośników i metodę obliczeniową.
W rzeczywistości formowanie gięciaZ drugiej strony, trudno jest dokładnie określić warstwę neutralną podczas procesu gięcia profili, co sprawia, że obliczenie odbicia jest trudniejsze. Obliczanie odbicia w przypadku gięcia profili jest znacznie bardziej złożone niż w przypadku gięcia płyt, więc metody obliczania odbicia w przypadku gięcia profili są znacznie bardziej złożone niż w przypadku gięcia płyt. gięcie rur są przybliżone i znacznie różnią się od rzeczywistej sytuacji.
Obecnie, zarówno w kraju, jak i za granicą, badania nad odbiciem wciąż trwają. Ponieważ odbicie wiąże się z wieloma czynnikami i jest dość złożone, obecnie nie ma dokładnej formuły obliczeniowej. Dlatego też kontrola wartości odbicia jest zazwyczaj korygowana przy użyciu form o różnych strukturach, głównie korygowanych podczas testowania form.
(3) Metody ograniczania i zapobiegania odbiciom
Metody redukcji i zapobiegania odbiciom można podzielić na dwie główne kategorie z perspektywy zasad. Pierwsza kategoria metod zapewnia kształt części po odbiciu poprzez zwiększenie deformacji. Główne działania w tej kategorii polegają na skorygowaniu kształtu formy, zmniejszeniu krzywizny gięcia części lub zwiększeniu kąta gięcia, tak aby część po odbiciu spełniała wymagania projektowe.
Inną kategorią metod jest zmniejszenie odbicia poprzez zmianę rozkładu naprężeń w wygiętej zdeformowanej części. W tej kategorii najczęściej stosowanym środkiem jest zastosowanie stycznego naprężenia rozciągającego, dzięki czemu rozkład naprężeń na przekroju wygiętej części jest jednolity, zmniejszając w ten sposób nierównomierność sprężystego powrotu podczas rozładunku i zmniejszając ilość odbicia.
Odbicie podczas formowania na zginanie jest jednym z głównych czynników wpływających na dokładność wymiarową i wydajność produkcji części. Ponieważ przewidywanie odbicia jest ściśle związane z całym procesem formowania, problem odbicia jest dość złożony i stanowi gorący i trudny punkt w badaniach nad formowaniem. gięcie profili formowanie. Wielu naukowców w kraju i za granicą przeprowadziło dogłębne badania i dyskusje.
Obecnie istnieje kilka metod radzenia sobie z problemem odbicia podczas gięcia rur:
1) Wymień tabelę danych odbicia na podstawie doświadczenia.
Na przykład, kilka krajowych stoczni zakupiło CNC giętarki do rur amerykańskiej firmy WALLACE COAST, które wykorzystują zestaw danych z doświadczenia w systemie sterowania do kompensacji odbicia. Jednak ze względu na duży błąd tej metody, dokładność gięcia giętarki CNC do rur nie jest idealna.
2) Wykorzystanie teoretycznych metod obliczeniowych.
Ponieważ sytuacja siłowa podczas gięcia rur jest bardzo złożona, podczas obliczeń należy przyjąć założenia i uproszczenia, a właściwości materiału i rzeczywiste warunki pracy są trudne do przewidzenia, jak dotąd nie znaleziono udanego precedensu wykorzystania teoretycznych formuł obliczeniowych odbicia w praktyce i potrzebna jest dalsza dyskusja.
3) W przemyśle lotniczym i samochodowym metoda reprezentowana przez amerykańską firmę EATON LEONARD jest stosowana od wielu lat.
Metoda ta zakłada, że chociaż istnieje wiele czynników wpływających na odbicie gięcia rur, po dostosowaniu obrabiarki parametry procesu (promień gięcia), a w tym czasie zależność między kątem gięcia a kątem formowania po odbiciu jest mierzona w warunkach gięcia partii rur materiałowych, dzięki czemu kąt obrotu ramienia giętarki do rur i kąt formowania rury można uznać za zależność liniową.
Metoda polega na zginaniu rur pod kątem 125° i 22° na giętarce do rur, a po zgięciu rur, umieszczeniu ich na maszynie CNC do pomiaru kształtu rur, aby zmierzyć ich rzeczywiste kąty formowania jako 120° i 20°, ustanawiając równanie linii prostej przez dwa punkty można uzyskać zależność między kątem skrętu ramienia giętarki do rur a wymaganym kątem formowania rury. Metoda ta przynosi dobre efekty.
Aby rozwiązać problem odbicia podczas gięcia rur, przeprowadzono następujące prace:
1) Przeprowadzono dużą liczbę eksperymentów z odbiciem.
Przeprowadzając eksperymenty gięcia rur bezrdzeniowych i rdzeniowych o różnych specyfikacjach na wielu giętarkach do rur i wykonując obliczenia analizy regresji na zmierzonych danych, wiadomo, że kąt gięcia α i kąt formowania α 0 zmienia się liniowo, co jest zgodne z teoretycznymi obliczeniami zmiany liniowej. Jednak inaczej, linia ta nie przechodzi przez początek, istnieje odległość przekroju C1 jak pokazano na rysunku 4-26.
α = K1 α0 + C1
We wzorze, K1 to nachylenie linii prostej;
C1 jest punktem przecięcia linii prostej.
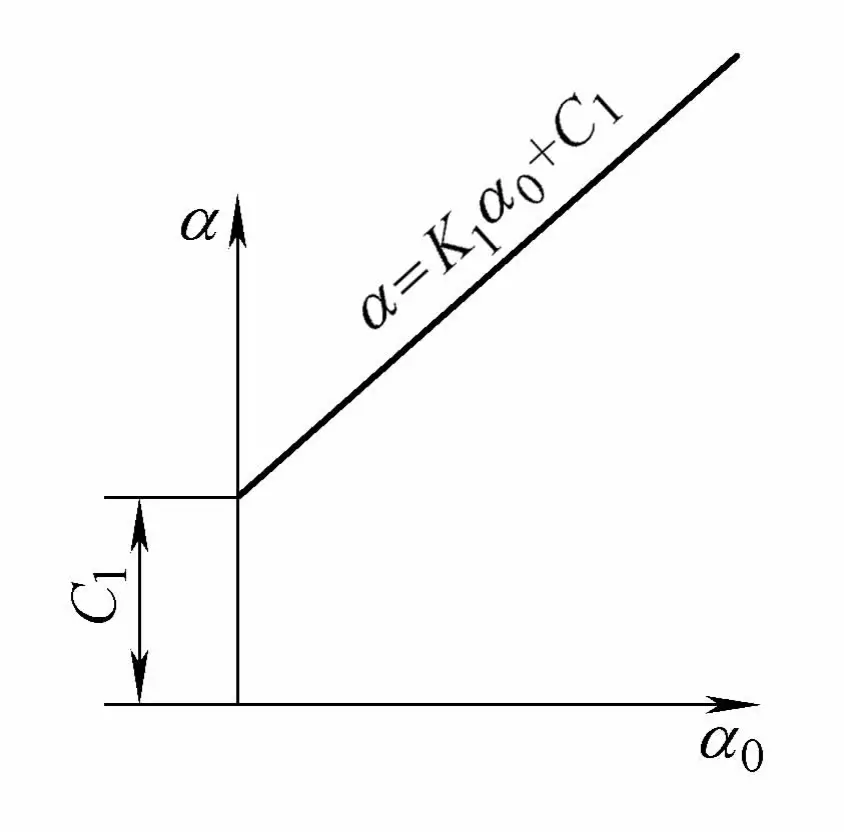
Z powyższego wzoru można wyciągnąć następujący wniosek: Dla rur giętych z tej samej partii materiału, w zakresie inżynierskich kątów gięcia, zależność między kątem gięcia α i kątem formowania α 0 jest zawsze linią prostą, która nie przechodzi przez punkt początkowy.
2) Teoretyczna analiza eksperymentu sprężystego zginania rur.
W celu przeanalizowania poprawności wniosków z eksperymentu sprężynowania przeprowadzono analizę siły dla warunków pracy giętarki do rur, a po przyjęciu pewnych założeń i uproszczeń wykonano dużą liczbę obliczeń.
Wyniki obliczeń pokazują, że w mniejszym zakresie kątów gięcia, zależność między kątem gięcia α i kątem formowania α 0 jest zakrzywiony, a po kącie gięcia jest większy niż 1, zależność między kątem gięcia α a kątem formowania α 0 jest liniowa i podąża za tym samym trendem, co liniowa zależność zaobserwowana podczas eksperymentu, tym samym wykazując poprawność wniosków z eksperymentu sprężystości.
Należy zauważyć, że istnieje znaczna różnica między tymi dwiema wartościami, co jest spowodowane założeniami i uproszczeniami przyjętymi w obliczeniach teoretycznych oraz faktem, że rzeczywiste warunki zginania rur są znacznie bardziej złożone niż sytuacje obliczeniowe.
W związku z tym wspomniana powyżej praca sięga głębiej niż wyniki badań reprezentowane przez firmę EATON LEONARD, która uważa "zależność między kątem skrętu ramienia giętarki do rur a kątem gięcia rury za liniową".
Podsumowując, najlepszą obecnie metodą radzenia sobie z problemem sprężynowania giętego materiału rurowego jest: podczas gięcia partii materiałów rurowych można przeprowadzić eksperymenty z dwoma różnymi kątami gięcia (na przykład 30° i 90°) na danej giętarce do rur. Podczas eksperymentu należy zapisać dwa rzeczywiste kąty obrotu ramienia giętarki α1 , α2 i zmierzyć dwa kąty formujące rury α01 , α02 . Następnie oblicz współczynniki za pomocą poniższego wzoru.
K1 = (α 2 - α 1 ) / (α 02 - α 01 )
C1 = α 1 - α 1 (α 2 - α 1 ) / (α 02 - α 01 )
Podstawiając powyższe dwa wzory do wzoru na α w eksperymencie odbicia, otrzymane równanie liniowe jest regułą odbicia dla tej partii materiału rury.
2. Wydłużenie przy zginaniu
Po gięciu na giętarce, długość osiowa rury o określonej długości zwiększy się, co jest zjawiskiem znanym jako wydłużenie gięcia. Wzrost długości osiowej nazywany jest wydłużeniem rury. Wydłużenie gięcia wpływa na dokładność wymiarową części. Metody stosowane w przeszłości w celu rozwiązania tego problemu obejmują:
1) Tabela danych wydłużenia oparta na doświadczeniu została opracowana do użytku produkcyjnego, ale metoda ta obarczona jest dużym błędem.
2) Metody obliczeniowe związane z teorią wydłużenia gięcia rur. Podobnie jak w przypadku odbicia, obecnie nie ma teoretycznej formuły obliczeniowej, która została z powodzeniem zastosowana w praktyce, co nadal wymaga dalszej dyskusji.
3) W przemyśle lotniczym i samochodowym od wielu lat stosowana jest metoda reprezentowana przez firmę EATON LEONARD, to znaczy podczas pomiaru odbicia za pomocą profilera rur CNC, tak zwana stała łuku jest obliczana za pomocą wzoru, który jest długością materiału używaną, gdy kąt gięcia wynosi 100 °, a także uważa się, że wydłużenie rury jest wprost proporcjonalne do kąta formowania.
Aby rozwiązać problem wydłużenia podczas gięcia rur, przeprowadzono następujące prace:
1) Przeprowadzono dużą liczbę eksperymentów wydłużania.
Przeprowadzając różne specyfikacje eksperymentów gięcia bezrdzeniowego i rdzeniowego na wielu maszynach do gięcia w pięciu stoczniach i wykonując obliczenia analizy regresji na danych uzyskanych z każdej partii materiałów, wiadomo, że wydłużenie △L ma liniową zależność od kąta formowania α', który nie przechodzi przez początek. To znaczy:
ΔL = K 2 α'+C 2
W formule,
- K 2 - nachylenie linii;
- C 2 - linia prosta.
Dzięki analizie regresji zmierzonych danych współczynnik korelacji γ wynosi od 0,97 do 0,99, co wskazuje na wyraźną zależność liniową. W związku z tym można wyciągnąć następujący wniosek: Dla rur z tej samej partii materiałów, w zakresie inżynierskich kątów gięcia, wydłużenie ΔL i kąt formowania α' mają liniową zależność, która nie przechodzi przez początek.
2) Weryfikacja regresji została również przeprowadzona na tabelach danych sprężynowania z powiązanych stoczni.
Z obliczeń empirycznych wiadomo, że wydłużenie ΔL i kąt formowania α' również mają zależność liniową, przy czym współczynnik korelacji γ wynosi powyżej 0,99, co wskazuje na wysoką liniowość, ale punkt przecięcia jest ogólnie mały.
3) Analiza teoretyczna eksperymentu wydłużania przy zginaniu rur.
Aby dodatkowo udowodnić poprawność wniosków z eksperymentu wydłużania, przeprowadzono analizę siły dla warunków gięcia rur giętarki do rur, a po przyjęciu pewnych założeń i uproszczeń wykonano dużą liczbę obliczeń. Wyniki obliczeń pokazują, że w małym zakresie kąta gięcia, wydłużenie ΔL i kąt formowania α' mają zależność krzywoliniową; gdy kąt gięcia jest większy niż 3°, wydłużenie ΔL i kąt formowania α' mają zależność liniową.
Zależność liniowa w części teoretycznej analizy i trend zależności liniowej podczas eksperymentu są takie same, co dowodzi poprawności wniosków z eksperymentu wydłużenia gięcia rur. Należy zauważyć, że istnieje znaczna różnica w wartościach między nimi, co jest spowodowane założeniami i uproszczeniami obliczeń teoretycznych, a rzeczywiste warunki gięcia rur są znacznie bardziej złożone niż sytuacje obliczeniowe.
Wniosek z badania, że dla rur z tej samej partii materiałów, w zakresie inżynierskich kątów gięcia, wydłużenie ΔL i kąt formowania α' mają liniową zależność, która nie przechodzi przez początek, różni się od tradycyjnie utrzymywanego poglądu, że wydłużenie jest wprost proporcjonalne do kąta formowania, przy czym ten pierwszy jest bardziej zgodny z rzeczywistą sytuacją gięcia rur przez giętarkę do rur.
Podsumowując, obecnie najlepszym podejściem do problemu wydłużenia gnącego materiału rurowego powinno być: podczas gięcia partii materiałów rurowych można przeprowadzić dwa eksperymenty gięcia o tej samej długości L, ale różnych zagięciach (na przykład 30° i 90°) na danej giętarce do rur. Po zakończeniu eksperymentu należy usunąć rury i zmierzyć dwa rzeczywiste kąty formowania α' 1 , α' 2 oraz zwiększone długości dwóch rzeczywistych osi rur L' 1 , L' 2 Następnie można obliczyć wydłużenie.
ΔL1 = (L1 '-L) ΔL2 = (L2 '-L)
Na tej podstawie współczynniki równania liniowego związanego z ΔL można obliczyć za pomocą następujących dwóch wzorów.
K 2 = (ΔL 2 -ΔL 1 ) / (α' 2 -α' 1 )
C 2 = ΔL 1 -α' 1 (ΔL 2 -ΔL 1 ) / (α' 2 -α' 1 )
Podstawiając powyższe dwa równania do równania liniowego dotyczącego ΔL, uzyskuje się prawo wydłużenia tej partii rur. Inteligentny przyrząd do pomiaru gięcia rur może wygodnie uzyskać to prawo wydłużenia.
3. Metoda radzenia sobie z problemem promienia formowania po gięciu rur i sprężynowania
Po wygięciu i odskoczeniu materiału rury, jej promień formowania R' staje się większy niż promień formy R, co spowoduje zmianę punktu stycznego rury. Dlatego też, podczas gięcia rur, giętarka powinna uwzględniać spowodowaną tym zmianę początkowego punktu gięcia. Metoda stosowana przez firmę EATON LEONARD polega na użyciu profilera rur CNC do pomiaru odpowiednich parametrów sprężynowania, a następnie obliczeniu promienia formowania po sprężynowaniu za pomocą wzoru i użyciu tego obliczonego promienia do skorygowania początkowego punktu gięcia.
Podczas korzystania z tego wzoru do radzenia sobie z początkowym punktem gięcia stwierdzono, że podczas gięcia rur o małych specyfikacjach (takich jak <3 mm), chociaż błąd jest większy, nadal można go wykorzystać; podczas gięcia rur o większych specyfikacjach błąd jest szczególnie duży, a efekt nie jest dobry. Wynika to również z bardzo złożonej sytuacji podczas gięcia rur oraz trudności w przewidywaniu właściwości materiału i rzeczywistych warunków pracy, co sprawia, że teoretyczny wzór obliczeniowy promienia formowania nie jest w stanie zaspokoić rzeczywistych potrzeb.
Jeśli początkowy punkt gięcia nie jest dobrze obsługiwany, trudno jest zapewnić dokładność formowania gięcia i wystąpią trudności podczas wdrażania procesu gięcia bez marży. Aby rozwiązać ten problem, należy stosować nowoczesne przyrządy pomiarowe.
Biorąc za obiekt określoną maszynę do gięcia rur, promień formowania partii materiałów rurowych po gięciu i sprężynowaniu jest faktycznie mierzony, co służy jako podstawa do radzenia sobie z początkowym punktem gięcia w procesie. Inteligentny przyrząd pomiarowy do gięcia rur może wygodnie uzyskać promień formowania materiału rury po gięciu i sprężynowaniu, a zasada obliczania pomiaru jest przedstawiona w poniższym wzorze obliczeniowym.
4. Metoda pomiaru sprężynowania, wydłużenia i promienia formowania za pomocą inteligentnego przyrządu pomiarowego do gięcia rur
Inteligentny przyrząd pomiarowy do gięcia rur opiera się głównie na wyżej wymienionej zasadzie gięcia rur, opracowanej specjalnie do użytku z giętarkami do rur CNC. Przyrząd składa się z urządzenia pomiarowego (w tym mechanizmu pomiarowego, czujnika kąta) i systemu mikrokomputerowego (w tym mikrokomputera, płyty interfejsu). Przyrząd charakteryzuje się wysoką precyzją, z kątem 0,1° i długością 0,25 mm.
Mechanizm pomiarowy przyrządu jest czteroprętowym mechanizmem płaskim, jak pokazano na rysunku 4-27, z czujnikiem kąta zainstalowanym w węzłach a, b i c, który może mierzyć kąt między dwoma sąsiednimi prętami. Głowice pomiarowe d i e są płaskie, więc podczas pomiaru pręty ad i be mogą być prostopadłe do prostego odcinka rury dghe.
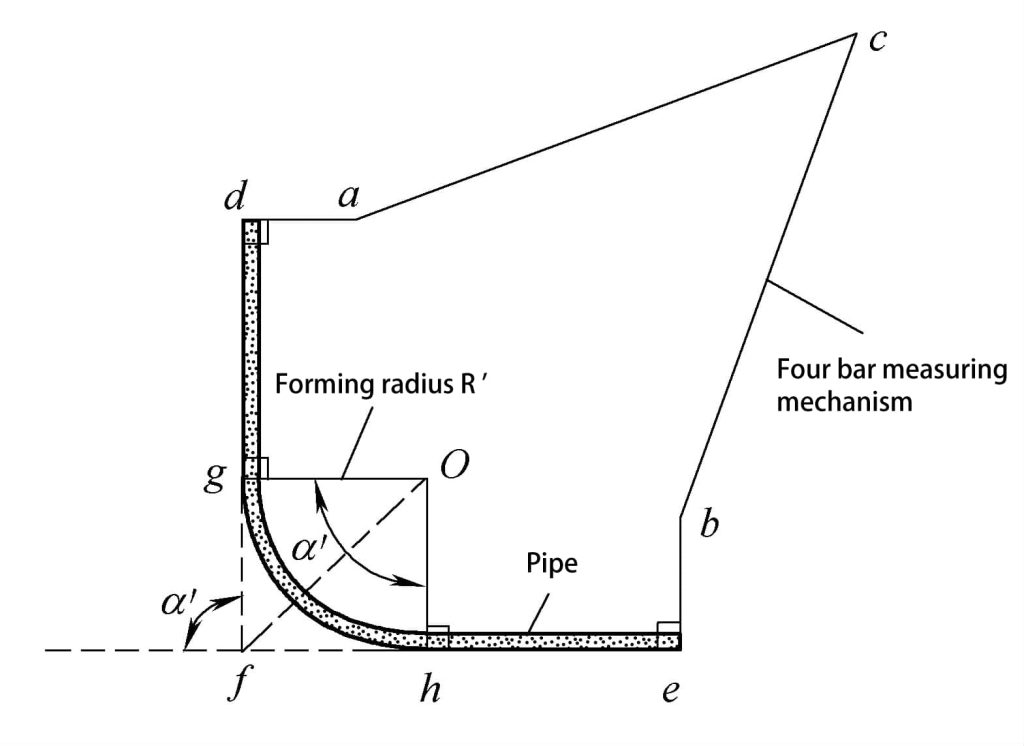
Długości każdego pręta w czterotaktowym mechanizmie płaskim są znane, więc można zmierzyć i obliczyć odpowiednie parametry geometryczne rury. Metoda jest następująca:
1) Na podstawie znanych warunków mechanizmu i kąta zmierzonego przez czujnik kąta można obliczyć kąt formowania α' rury.
2) Na podstawie znanych warunków mechanizmu i kąta zmierzonego przez czujnik kąta można obliczyć odległości df i fe punktów przecięcia osi prostej rury.
3) Gdy odległość dg od początkowego punktu gięcia rury dopasowanie jest znany, rzeczywisty promień formowania R' można dalej obliczyć.
R'=O g = (df-dg) / tan(α'/2)
4) Długość L' osi rury może być dalej obliczana.
L’=df+fe-2R’tan(α’/2) +πR’α’/180
W oparciu o powyższe zasady i wzory konieczne jest jedynie wygięcie dwóch elementów testowych o tej samej długości L i początkowych punktach gięcia odpowiednio w odległościach d i g na giętarce do rur pod ustalonymi kątami (H 1 =30°, H=90°), a następnie usunąć je i zmierzyć za pomocą inteligentnego przyrządu pomiarowego do gięcia rur, który może automatycznie zakończyć rzeczywisty pomiar i wydrukować wzór zmiany odbicia, wzór zmiany wydłużenia i uformowany promień po odbiciu różnych materiałów metalowych i modeli rur.
W przypadku podania kształtu rury przedmiotu obrabianego, przyrząd może również dostarczyć dane wykroju do gięcia bez naddatku, a także może dostarczyć program obróbki dla giętarki CNC do rur, w tym korektę punktu początkowego i kompensację odbicia (przyrząd ma również funkcję pomiaru kształtu rury). Dane dostarczane przez przyrząd nie tylko znacznie poprawiają dokładność formowania giętarki CNC do rur, ale także promują postęp technologiczny, osiągając cel zmniejszenia pracochłonności, oszczędności stali i poprawy wydajności produkcji.
5. Promień gięcia
Stopień odkształcenia zginającego materiału rury zależy od wartości względnego promienia gięcia R/D i względnej grubości t/D (R to promień krzywizny środkowej warstwy przekroju poprzecznego materiału rury, D to zewnętrzna średnica materiału rury, t to grubość ścianki materiału rury). Im mniejsze wartości R/D i t/D, tym większy stopień odkształcenia przy zginaniu, zewnętrzna ściana warstwy neutralnej przy zginaniu stanie się nadmiernie cienka, prowadząc nawet do pęknięcia; najbardziej wewnętrzna ściana pogrubi się, stając się nawet niestabilna i pomarszczona.
Jednocześnie, wraz ze wzrostem stopnia odkształcenia, zniekształcenie przekroju poprzecznego (spłaszczenie) również staje się bardziej dotkliwe. Dlatego też, aby zapewnić jakość formowania materiału rury, konieczne jest kontrolowanie stopnia odkształcenia w dopuszczalnym zakresie. Dopuszczalny stopień odkształcenia przy gięciu materiału rury nazywany jest granicą formowania przy gięciu. Granica formowania gięcia materiału rury zależy nie tylko od właściwości mechanicznych materiału i metody gięcia, ale także od wymagań dotyczących stosowania łączników rurowych.
W przypadku części giętych ogólnego przeznaczenia, warunkiem zdefiniowania granicy formowania jest maksymalne odkształcenie wydłużenia ε maks wytworzona w miejscu najbardziej oddalonym od warstwy neutralnej na zewnętrznej części obszaru odkształcenia zginającego nie powinna przekraczać wartości granicznej dozwolonej przez plastyczność materiału.
Pod warunkiem, że zewnętrzna warstwa powierzchniowa poza obszarem odkształcenia złączki rurowej nie pęka, graniczny promień gięcia r min którą można wygiąć do wewnętrznej strony części, jest używana jako granica formowania gięcia złączki rurowej. r min jest związana z właściwościami mechanicznymi materiału, rozmiarem konstrukcji łącznika rurowego, metodą obróbki gięcia i innymi czynnikami.
Minimalny promień gięcia dla różnych metod gięcia przedstawiono w tabeli 4-6.
Tabela 4-6 Minimalny promień gięcia dla gięcia rur (jednostka: mm)
| Metody gięcia | Minimalny promień gięcia (rmin) |
| Gięcie na prasie | (3~5)D |
| Gięcie owijki | (2~2.5)D |
| Gięcie rolkowe | 6D |
| Push Bending | (2.5~3)D |
Uwaga: D to zewnętrzna średnica rury.
Minimalny promień gięcia dla rur stalowych i aluminiowych przedstawiono w tabeli 4-7.
Tabela 4-7 Minimalny promień gięcia dla rur stalowych i aluminiowych (jednostka: mm)
| Średnica zewnętrzna rury | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| Minimalny promień gięcia rmin | 8 | 12 | 16 | 20 | 28 | 32 | 40 | 45 | 50 | 56 |
| Średnica zewnętrzna rury | 24 | 28 | 30 | 32 | 35 | 38 | 40 | 44 | 48 | 50 |
| Minimalny promień gięcia rmin | 68 | 84 | 90 | 96 | 105 | 114 | 120 | 132 | 144 | 150 |

