W przypadku części giętych z blachy, obliczenie rozmiaru półfabrykatu jest warunkiem wstępnym do sformułowania planu procesu gięcia. Różni technicy mogą wybrać różne współczynniki naddatku na gięcie w swoich dokumentach procesowych, a dokładność rozmiaru półfabrykatu ma bezpośredni wpływ na dokładność wymiarową i jakość produktu giętych części.
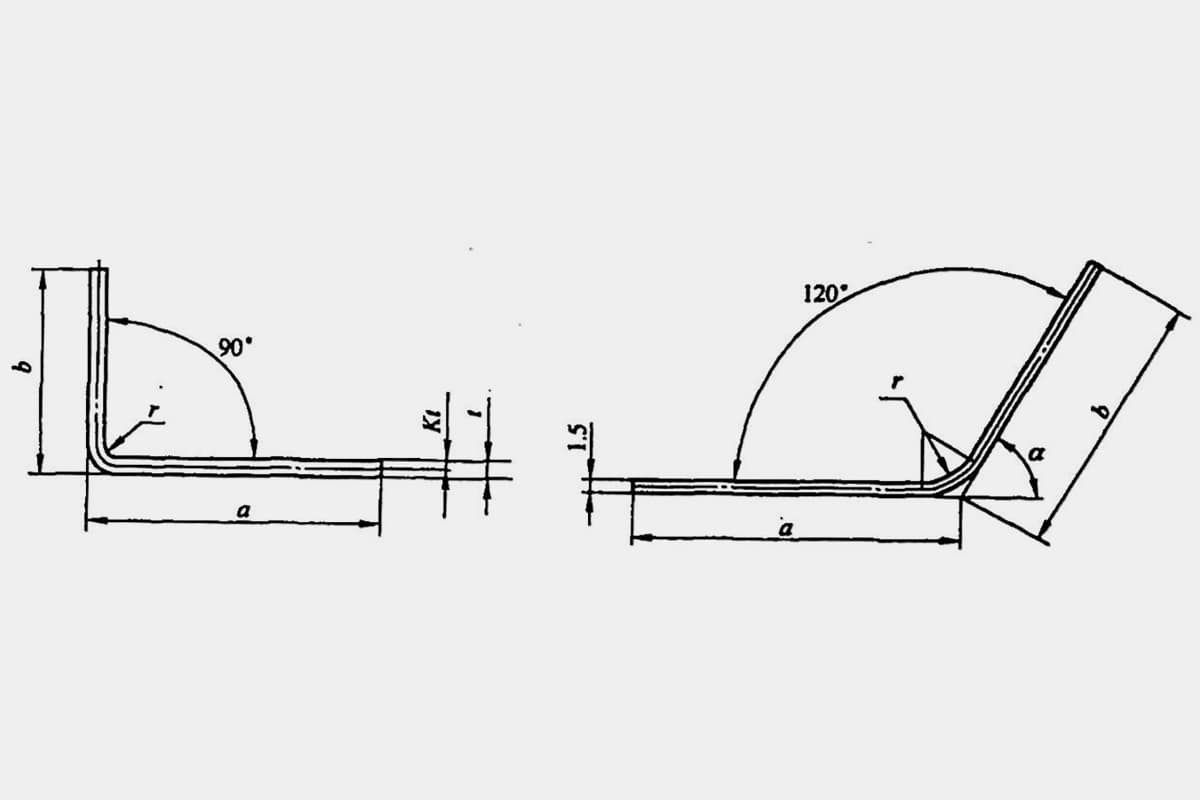
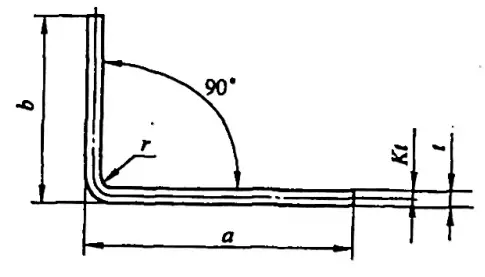
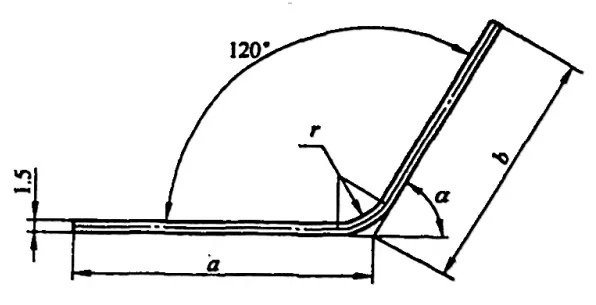
Czasami niedokładne obliczenia mogą nawet skutkować odpadami. Rozłożona długość L typowej prostej części giętej (patrz rysunek 5-1) wynosi L = a + b - y (gdzie y jest odjęciem gięcia, znanym również jako wartość korekcji dla części R).
Jednakże, w różnych podręcznikach i materiałach, odliczenie zginania dla φ = 90° można uzyskać bezpośrednio, podczas gdy dla zgięć innych niż 90°, jak pokazano na rysunku 5-2, technicy muszą obliczyć je na podstawie współczynnika doświadczenia (współczynnik K).
Powiązana lektura: Wyjaśnienie sztuki rozkładania blachy
1. Zasada obliczania rozłożonego wymiaru zagięć blachy
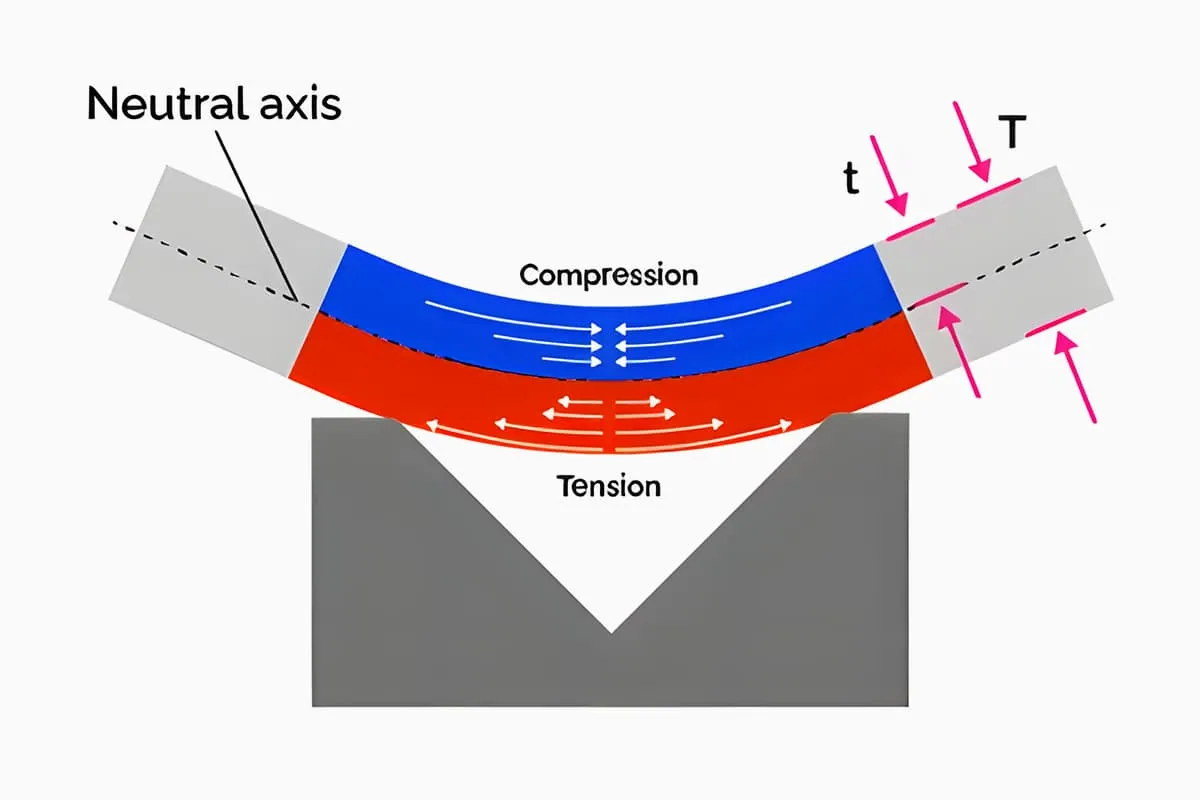
Rozłożony wymiar giętego półfabrykatu jest określany w oparciu o zasadę, że długość warstwy neutralnej pozostaje niezmieniona przed i po gięciu. Gdy blacha jest zginana, włókna warstwy zewnętrznej sekcji półfabrykatu są rozciągane, a włókna warstwy wewnętrznej są ściskane.
Rozciąganie włókien warstwy zewnętrznej stopniowo zmniejsza się od zewnątrz do wewnątrz, a ściskanie włókien warstwy wewnętrznej również stopniowo zmniejsza się od wewnątrz na zewnątrz.
Gdy włókna przechodzą od rozciągania do ściskania lub od ściskania do rozciągania, musi istnieć warstwa włókien, w której naprężenie i odkształcenie są zerowe, a ich długość pozostaje niezmieniona przed i po zginaniu.
Warstwa ta jest tym, co definiujemy jako warstwę neutralną. Dlatego kluczem do obliczenia rozłożonego wymiaru wygiętego półfabrykatu jest określenie położenia warstwy neutralnej. Położenie warstwy neutralnej jest określane na podstawie warunku, że objętość wygiętej części i półfabrykatu są równe przed i po odkształceniu plastycznym.
2. Wyznaczanie promienia krzywizny ρ warstwy neutralnej
Teoretycznie, ze względu na nierównomierne odkształcenie wzdłuż kierunku grubości wygiętej części, warstwa neutralna jest powierzchnią paraboliczną, ale do celów obliczeniowych jest zwykle uważana za powierzchnię łuku kołowego. Gdy odkształcenie przy zginaniu jest bardzo małe (r/t >6,5), warstwę neutralną można w przybliżeniu uznać za znajdującą się w środku grubości materiału, to znaczy promień krzywizny warstwy neutralnej wynosi ρ=r+t/2.
Gdy odkształcenie jest bardzo duże (r/t≤6,5), grubość materiału staje się cieńsza, a odkształcenie przekroju jest bardzo duże, jak pokazano na rysunku 5-3.
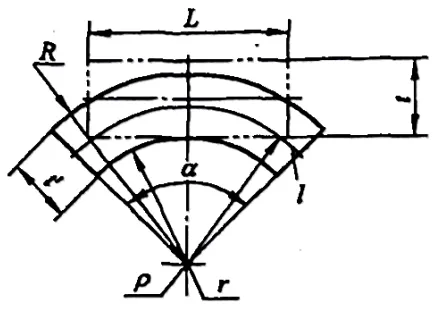
W tym momencie, aby spełnić warunek równowagi, zgodnie z którym siła wypadkowa wszystkich sił działających w sekcji wynosi zero, warstwa neutralna musi przesunąć się w kierunku wewnętrznej powierzchni materiału.
W tym momencie możemy określić promień krzywizny warstwy neutralnej w oparciu o warunek, że objętość nie zmienia się podczas odkształcenia plastycznego, czyli objętość przed zginaniem: V0=LBt, oraz objętość po zginaniu:
V=(R2-r2)α*B'/2.
We wzorze, B to szerokość półfabrykatu (mm); B' to średnia szerokość półfabrykatu po gięciu (mm); α to kąt środkowy gięcia. Zgodnie z zasadą, że objętość jest równa przed i po gięciu, mamy V0=V, to znaczy,
LBt=(R2-r2)α*B'/2, oraz L=(R2-r2)α*B'/2tB (5-1).
Z zerowego naprężenia i odkształcenia warstwy neutralnej otrzymujemy L=l=αρ, gdzie L jest długością przed odkształceniem warstwy neutralnej (mm), a l jest długością po odkształceniu warstwy neutralnej (mm).
Podstawiając równanie (5-1), otrzymujemy ρ=(R2-r2)B'/2tB. Jeśli podstawimy R=r+t' do powyższego równania, możemy otrzymać inną postać równania ρ=(r/t+η/2)tβη (5-2)gdzie β jest współczynnikiem szerokości, β=B'/B, a ogólnie, gdy gięta jest szeroka płyta (B>3t), zwykle uważa się, że β=1; η jest współczynnikiem rozrzedzenia, η=t'/t.
Równanie (5-2) jest wzorem do teoretycznego obliczania położenia warstwy neutralnej. Podczas obliczeń musimy znać η, czyli regułę przerzedzania. Wartość η można znaleźć w tabeli 5-1.
Należy zaznaczyć, że reguła przerzedzania jest dość złożona, rozkład położenia warstwy neutralnej w obszarze gięcia nie jest jednolity, a reguła przerzedzania jest również związana z wieloma czynnikami, takimi jak metoda gięcia, szerokość dolnej szczeliny matrycy gnącej i grubość materiału.
Powoduje to nieuniknione błędy w teoretycznych obliczeniach położenia warstwy neutralnej, zmniejszając w ten sposób praktyczną wartość zastosowania teoretycznej metody określania.
Tabela 5-1: Współczynnik rozrzedzenia η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
W rzeczywistej produkcji, wzór empiryczny, który jest prostszy niż teoretyczne obliczenia, jest zwykle używany do określenia położenia osi neutralnej, jak poniżej:
ρ = r + Kt (5-3)
Gdzie:
- ρ - Promień krzywizny osi neutralnej (mm)
- r - Wewnętrzny promień gięcia surowca (mm)
- t - grubość materiału (mm)
- K - Współczynnik osi neutralnej (empiryczny) Współczynnik K), patrz Tabela 5-2
Tabela 5-2: Wartości empiryczne współczynnika osi obojętnej K
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
Uwaga:
- K1 ma zastosowanie do zagięć w kształcie litery V lub U z płytą górną lub płytą dociskową.
- K2 nadaje się do łuków w kształcie litery V bez płyty górnej.
3. Obliczanie wymiarów półfabrykatu po rozłożeniu dla kilku typowych zagięć blachy
W oparciu o definicję warstwy neutralnej, wymiar rozłożonego półfabrykatu powinien być równy długości warstwy neutralnej. Zazwyczaj, w oparciu o wewnętrzną promień gięcia r półfabrykatu, zagięcia są klasyfikowane jako zaokrąglone i niezaokrąglone: zagięcia są uważane za zaokrąglone, gdy r>0,5t, i niezaokrąglone, gdy r<0,5t.
Ponadto, w oparciu o szerokość płyty B, zagięcia są podzielone na szerokie i wąskie: gdy szerokość płyty B>3t, jest to określane jako szerokie zagięcie płyty, a gdy szerokość płyty B<3t, jest to określane jako wąskie zagięcie płyty.
W praktyce produkcyjnej najczęściej stosowane są łuki o promieniu zaokrąglenia (r>0,5t) i szerokie blachy (B>3t), a biorąc pod uwagę uniwersalność łuków, omawiamy głównie obliczenia wymiarów rozłożonego półfabrykatu dla łuków o promieniu zaokrąglenia i szerokich blach podczas gięcia.
3.1 Obliczanie wymiarów półfabrykatu po rozłożeniu dla łuków okrągłych (r>0,5t)
Gdy r>0,5t, B>3t, ze względu na przerzedzenie części zginanej nie jest poważne, a zniekształcenie przekroju jest niewielkie, długość półfabrykatu można określić w oparciu o zasadę, że długość warstwy neutralnej jest równa wymiarowi rozłożonego półfabrykatu.
Powszechnie stosowane metody obliczania wymiarów rozwiniętego półfabrykatu dla łuków o zaokrąglonych narożach (r>0,5t) dzielą się na: obliczanie współczynnika zginania i obliczanie wartości odliczenia zginania.
1. Zagięcia o zaokrąglonych narożnikach (r>0,5t) Obliczanie współczynnika gięcia dla wymiarów po rozłożeniu półfabrykatu:
1) Współczynnik zginania to długość części łuku mierzona wzdłuż warstwy neutralnej strefy odkształcenia przy zginaniu (część R przy zginaniu), jak pokazano na rysunku 5-4.
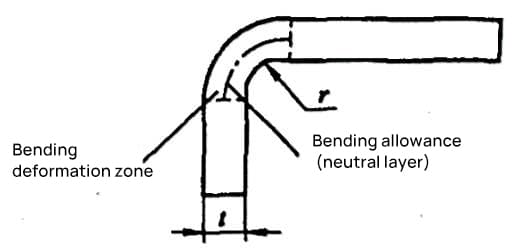
Współczynnik zginania oblicza się według wzoru (5-4): x=παρ/180° (5-4)
Gdzie ρ jest promieniem krzywizny warstwy neutralnej (mm).
2) Rysunek 5-5 przedstawia przykład notacji wymiarowej do obliczania współczynnika zginania wymiarów rozłożonego półfabrykatu, a jego wzór do obliczania współczynnika zginania wymiarów rozłożonego półfabrykatu jest następujący.

a) φ > 90° b) φ≤90
L=a+b+x (5-5)
Podstawiając równanie (5-3) do równania (5-4), otrzymujemy wzór na współczynnik zginania:
x=πα(r+Kt)/180° (5-6)
Podstawiając równanie (5-6) do równania (5-5), otrzymujemy wzór na obliczenie rozłożonego rozmiaru wygiętego półfabrykatu:
L=a+b+πα(r+Kt)/180° (5-7)
Gdzie:
- L - Rozłożony rozmiar półfabrykatu (mm);
- K - Współczynnik K, jego wartość można znaleźć w tabeli 5-2;
- α - centralny kąt zgięcia, jego związek z kątem zgiętej części wynosi α=180°-φ;
- r - promień gięcia wewnętrznej warstwy półfabrykatu (mm);
- t - grubość materiału (mm);
- a, b - odpowiednio długości prostych części elementu (mm).
2. Obliczenie potrącenia na zginanie dla rozłożonego rozmiaru części giętej z zaokrąglonym narożnikiem (r>0,5t)
1) Odliczenie zginania (znane również jako wartość korekty dla części R) jest różnicą między dwukrotnością R strefy odkształcenia zginania (część R zgięcia) a współczynnikiem zginania, jak pokazano na rysunku 5-6.

Odliczenie gięcia (wartość korekty dla części R) jest obliczane zgodnie z równaniem (5-8):
y = 2R-παr/180° (5-8)
2) Rysunek 5-7 przedstawia przykład adnotacji wymiarowej do obliczania potrącenia na zginanie dla rozłożonego rozmiaru półfabrykatu. Odjęcie na zginanie y jest obliczane według następującego wzoru:
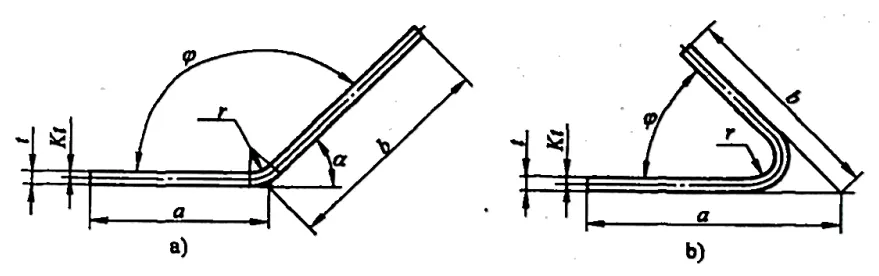
a)90°<φ≤165° b)φ≤90°
① Gdy φ ≤ 90°:
R=(r+t)/tan(φ/2)
Podstawiając powyższy wzór i wzór (5-3) do wzoru (5-8), otrzymujemy odjęcie zginania (tj. wartość korekcji części R) dla zgięcia φ≤90° (patrz rysunek 5-7b):
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
② Gdy 90°<φ≤165°:
R=(r+t)tan[(180°-φ)/2]
Podstawiając powyższy wzór i wzór (5-3) do wzoru (5-8), otrzymujemy odjęcie zginania (tj. wartość korekcji części R) dla zgięcia 90°<φ≤165° (patrz rysunek 5-7a):
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
③ Gdy 165°<φ≤180°:
y≈0
3) Wzór na obliczenie wartości potrącenia na zginanie dla rozmiaru półfabrykatu części pokazanej na rysunku 5-7 jest następujący:
L=a+b-y (5-11)
① Gdy φ≤90°, podstawiając wzór (5-9) do wzoru (5-11), otrzymujemy następujący wzór do obliczania wartości odliczenia gięcia dla rozmiaru półfabrykatu:
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
② Gdy 90°<φ≤165°, podstawiając wzór (5-10) do wzoru (5-11), otrzymujemy następujący wzór do obliczania wartości odliczenia gięcia dla rozmiaru półfabrykatu:
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
③ Gdy 165°<φ≤180°:
L≈a+b (5-14)
Gdzie,
- y - Odejście przy zginaniu (mm)
- L - rozmiar pustej części (mm)
- r - Wewnętrzny promień gięcia półfabrykatu (mm)
- t - grubość materiału (mm)
- α - środkowy kąt gięcia, jego związek z kątem gięcia wynosi α=180°-φ
- a, b - Długości krawędzi części (mm) do wierzchołka gięcia.
3. Obliczanie rozmiaru półfabrykatu dla łuków wielokątowych
W przypadku zagięć pod wieloma kątami rozmiar półfabrykatu jest sumą części R i długości prostych krawędzi.
1) Obliczanie rozmiaru półfabrykatu giętego pod wieloma kątami na podstawie współczynnika gięcia:
L=l1+l2+...+ln+1+nx (5-15)
Gdzie l1, l2...ln+1 są długościami prostych części każdej krawędzi części (mm);
n to liczba zagięć R.
2) Obliczanie rozmiaru półfabrykatu giętego pod wieloma kątami na podstawie odliczenia gięcia:
L=l1+l2+...+ln+1-ny (5-16)
Gdzie l1, l2...ln+1 są długościami krawędzi części (mm) do wierzchołka gięcia;
n to liczba zagięć R.
Przykład 5-1: Oblicz rozmiar półwyrobu dla zagięcia pokazanego na rysunku 5-8.
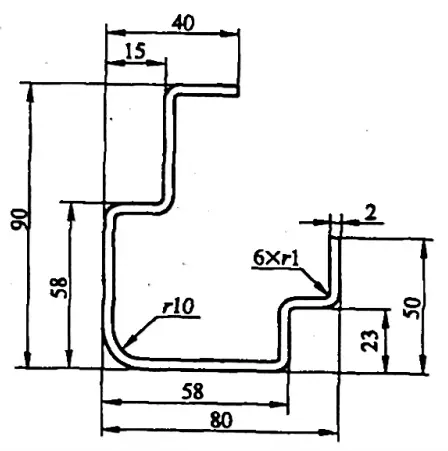
Rozwiązanie 1: Oblicz rozmiar półfabrykatu przy użyciu współczynnika zginania.
Patrz Załącznik A: Gdy kąt gięcia elementu φ=90°, grubość t=2 mm i promień r=10 mm, współczynnik gięcia wynosi 2,68 mm;
Gdy kąt gięcia elementu wynosi 90°, grubość t=2mm, a promień r=10mm, współczynnik gięcia wynosi x2=16,9mm.
Z równań (5-5) i (5-15), płaski rozmiar półfabrykatu dla elementu giętego jest obliczany jako:
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2,68 + 16,9]mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240,98 mm.
Rozwiązanie 2: Oblicz płaski rozmiar półfabrykatu przy użyciu wartości odliczenia gięcia.
Patrz Załącznik C: Dla łuku o kącie φ=90°, grubości t=2mm i promieniu r=1mm, wartość korekcji dla sekcji R wynosi y1=3,32mm; dla łuku o kącie φ=90°, grubości t=2mm i promieniu r=10mm, wartość korekcji dla sekcji R wynosi y2=7,1mm.
Surowy rozmiar wygiętej części można uzyskać z równań (5-11) i (5-16):
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3.32 - 7.1] mm
= (25+34+17+116+25+24+27-19.92-7.1) mm
= 240,98 mm
Przykład 5-2: Oblicz surowy rozmiar wygiętej części pokazanej na rysunku 5-9.
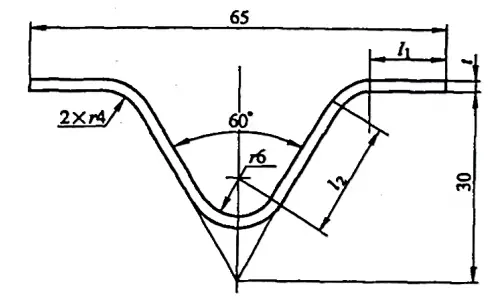
Rozwiązanie: Oblicz rozmiar surowy przy użyciu współczynnika zginania.
Wzór na obliczenie wymiarów półfabrykatu wygiętej części z równań (5-5) i (5-15) jest następujący:
L=2l1+2l2+2x1+x2
gdzie l1 = [32,5 - (30tan30°+4tan30°)] mm = 12,87 mm
i l2 = [(30/cos30°) - (8/tan30°+4tan30°)] mm = 18,47 mm
Odwołując się do Załącznika A: gdy kąt zgięcia φ=120°, t=2mm, r=4mm, wartość współczynnika zginania wynosi x1=4,98mm; gdy kąt zgięcia φ=60°, t=2mm, r=6mm, wartość współczynnika zginania wynosi x2=14,16 mm.
Podstawienie tych wartości do wzoru daje długość rozłożonego półfabrykatu jako L= (2×12,87 + 2×18,47 + 2×4,98 + 14,16) mm = 86,8 mm.
Należy zauważyć, że w przypadku prostszych gięć o niższych wymaganiach dotyczących precyzji, wymiary rozłożonego półfabrykatu można obliczyć bezpośrednio. Jednak w przypadku bardziej złożonych gięć lub tych o wyższych wymaganiach dotyczących precyzji, kształt i wymiary rozłożonego półfabrykatu muszą być wielokrotnie testowane i stale weryfikowane w celu potwierdzenia kształtu i wymiarów półfabrykatu.
3.2 Obliczanie wymiarów rozwinięcia półfabrykatu dla elementów o ostrym zagięciu (r<0,5t)
Gdy promień gięcia r elementu jest mniejszy niż 0,5 t, określa się go jako gięcie ostre. Obliczenie wymiaru rozwinięcia półfabrykatu dla takich komponentów opiera się na zasadzie spójności objętości przed i po gięciu.
W przypadku ostrych zagięć, ze względu na znaczne rozrzedzenie materiału w miejscu zagięcia, proces deformacji jest niezwykle złożony, co utrudnia dokładne obliczenie wymiarów rozwinięcia półfabrykatu. Dlatego też obliczone wymiary rozwinięcia półfabrykatu muszą zostać skorygowane w oparciu o dane empiryczne lub poprzez próbne gięcie.
Wzór obliczeniowy dla wymiarów rozwinięcia półfabrykatu elementów giętych na ostro (r<0,5t, φ=90°) można znaleźć w tabeli 5-3.
Tabela 5-3 Wzór obliczeniowy dla wymiarów rozwinięcia półfabrykatu elementów giętych na ostro (r<0,5t, φ=90°) (jednostka: mm)
| Numer seryjny | Funkcje gięcia | Schemat | Formuła |
| 1 | Zagięcie rogu. |  | L=a+b+0.4t |
| 2 | Spłaszcz go. |  | L=a+b-0.43t |
| 3 | Zagnij dwa rogi jednocześnie. | 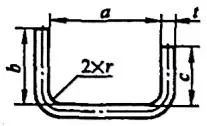 | L=a+b+c+0.6t |
| 4 | Zegnij trzy rogi jednocześnie. | 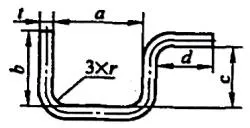 | L=a+b+c+d+0.75t |
| 5 | W pierwszym przypadku zagnij dwa rogi, a w drugim zagnij kolejny róg. | L=a+b+c+d+t | |
| 6 | Zegnij cztery rogi jednocześnie. | 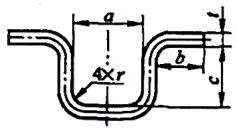 | L=a+2b+2c+1.2t |
| 7 | Wygiąć, aby utworzyć cztery narożniki w dwóch miejscach. | L=a+2b+2c+1.2t |
3.3 Obliczanie wymiarów po rozłożeniu dla części giętych typu zawiasowego
Dla zawiasów części do gięcia z r= (0,6~3,5)t (patrz Rysunek 5-10), proces wywijania zwykle przebiega zgodnie ze schematem pokazanym na Rysunku 5-11. Podczas wywijania grubość blachy wzrasta, a warstwa neutralna przesuwa się na zewnątrz. Rozłożone wymiary półfabrykatu można w przybliżeniu obliczyć za pomocą następującego wzoru:
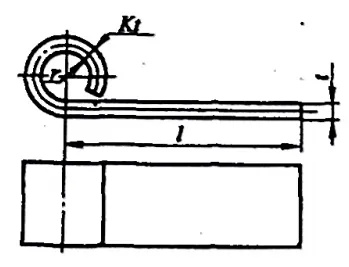
- a) Pierwsza operacja
- b) Druga operacja
L=l+1.57π(r+Kt)+r
Gdzie:
- L - Rozłożone wymiary półfabrykatu (mm);
- l - długość odcinka prostego (mm);
- r - Wewnętrzny promień gięcia półfabrykatu (mm);
- K - współczynnik przemieszczenia warstwy neutralnej. Gdy r/t=0,5~1,8, K jest zwykle przyjmowane jako 0,5~0,70 (im mniejsza wartość r/t, tym większa wartość K; odwrotnie, im mniejsza wartość K). Można ją również wybrać zgodnie z tabelą 5-4.
Tabela 5-4 Współczynnik przemieszczenia warstwy neutralnej dla części zginanych typu zawiasowego
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |