Podczas procesu tworzenia rysunku rozwojowego elementu blaszanego konieczne jest również uwzględnienie wpływu grubości przetwarzanego materiału, czyli dokonanie odpowiednich korekt grubości blachy.
Ogólnie rzecz biorąc, w przypadku materiałów arkuszowych o grubości mniejszej niż 3 mm nie jest wymagana regulacja grubości blachy. Można ją obliczyć zgodnie z centralną średnicą materiału arkusza lub zgodnie z liniami cięcia powierzchni wewnętrznej i zewnętrznej. Wymiary po formowaniu mieszczą się w dopuszczalnym zakresie odchyleń. Gdy grubość blachy jest większa niż 3 mm, należy ją obliczyć zgodnie z centralną średnicą materiału blachy. Dla wygody opisu, obliczenia dla poniższych opracowanych materiałów odnoszą się do centralnej średnicy arkusza materiału.
1. Obliczanie rozwoju powłok cylindrycznych
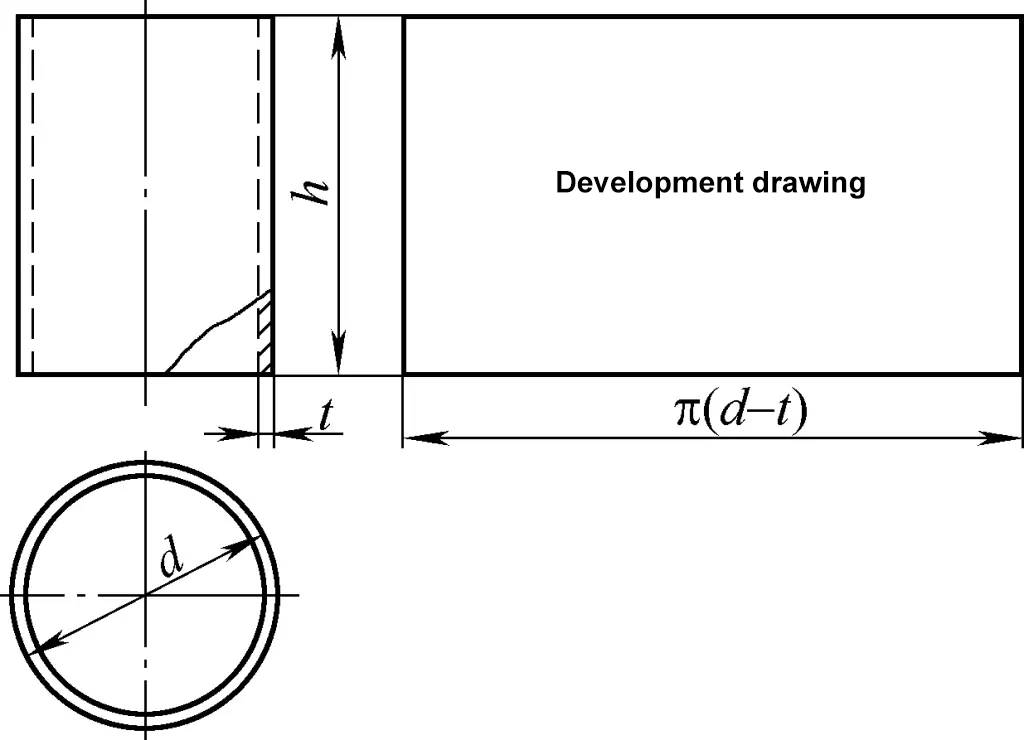
Cylindryczna powłoka należy do powierzchni cylindrycznej, a jej rysunek rozwinięcia jest prostokątem. Jeden bok prostokąta jest równy obwodowi cylindra π(d-t), a drugi bok to wysokość h cylindra, jak pokazano na rysunku 1. Na rysunku d jest zewnętrzną średnicą cylindra, a t jest grubością płyty.
2. Obliczanie rozwoju stożków kołowych prostych
Rysunek rozwinięcia prawego stożka kołowego jest łukiem sektorowym. Wzór obliczeniowy dla rysunku rozwinięcia prawego stożka kołowego pokazanego na rysunku 2 jest następujący:
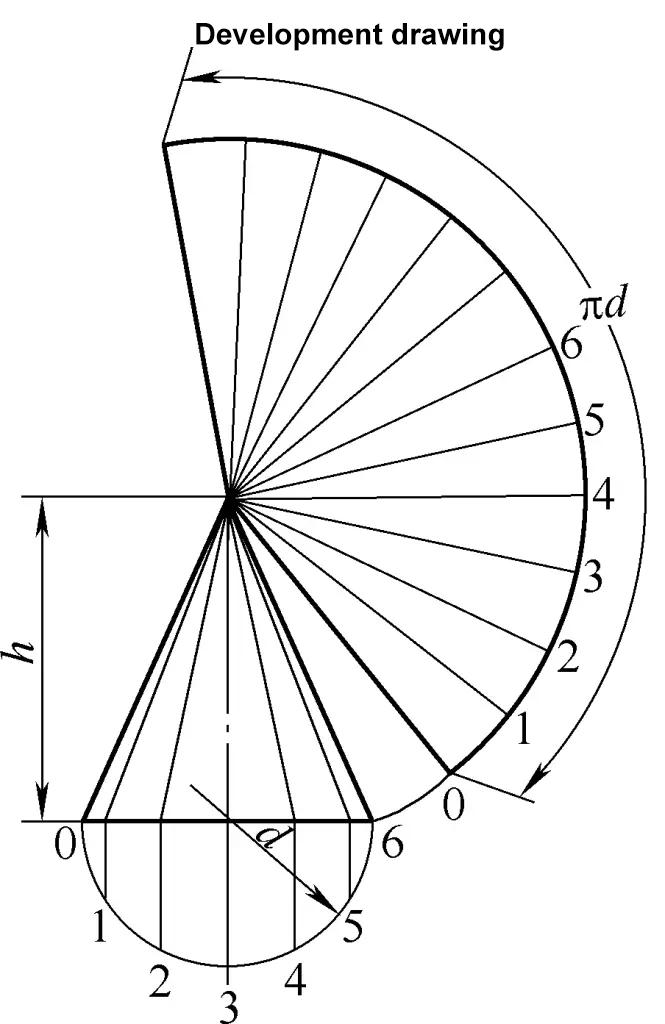
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
W formule
- R - Promień łuku sektora (mm);
- α - kąt sektora (°);
- L - długość cięciwy łuku sektorowego (mm).
3. Obliczanie rozwoju ściętych prawych stożków kołowych
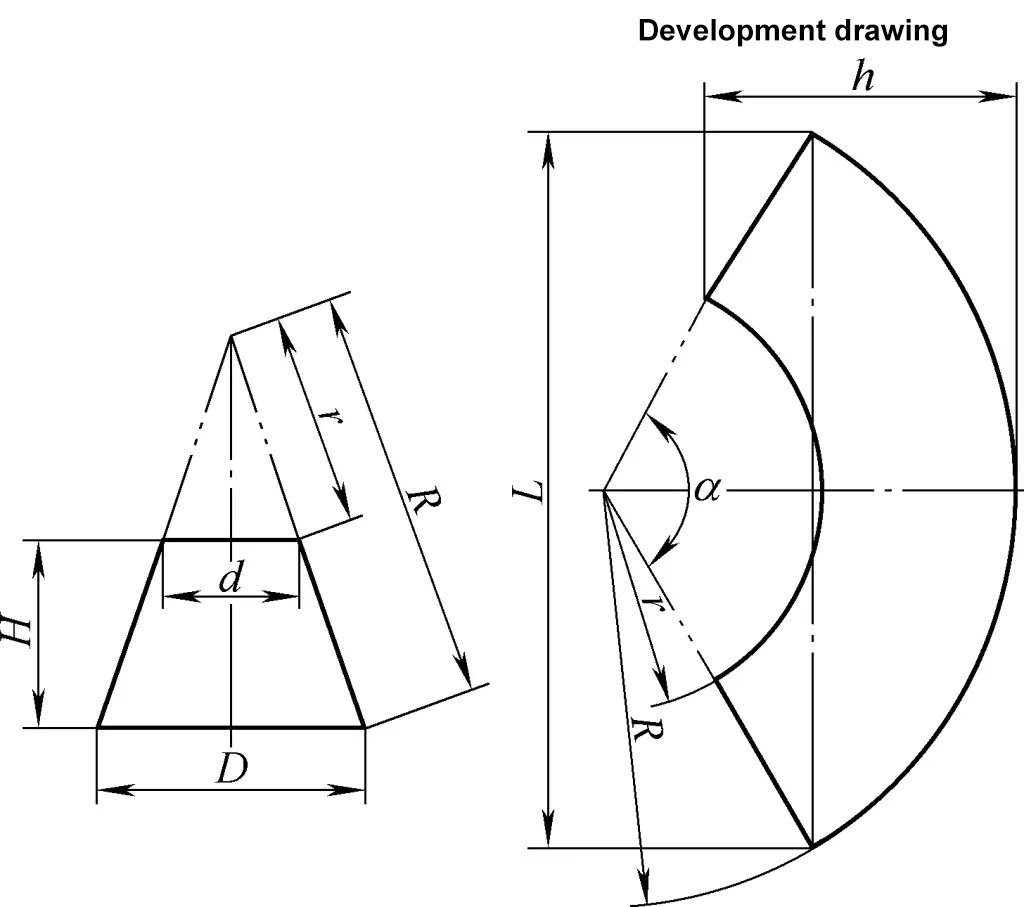
Rysunek rozwinięcia ściętego prawego stożka kołowego jest koncentrycznym łukiem sektorowym. Wzór obliczeniowy dla rysunku rozwinięcia ściętego prawego stożka kołowego pokazanego na rysunku 3 to:
R=√{(D/2)2+[DH/(D-d)]2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
Gdy α>180°, h=R+rsin[(α-180)/2]
Znaczenie symboli we wzorze można znaleźć na rysunku 3.
4. Obliczanie rozwoju skośnych prawych stożków kołowych
Rysunek rozwinięcia ukośnego prawego stożka kołowego jest nieregularnym łukiem sektorowym. Wzór obliczeniowy dla rysunku rozwinięcia ukośnego prawego stożka kołowego pokazanego na rysunku 4 jest następujący:
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[(A-D/2cosαn)2+(D/2)2grzech2αn+H2]
yn=fn(1-h/H)
m=Dsin(180°/n )
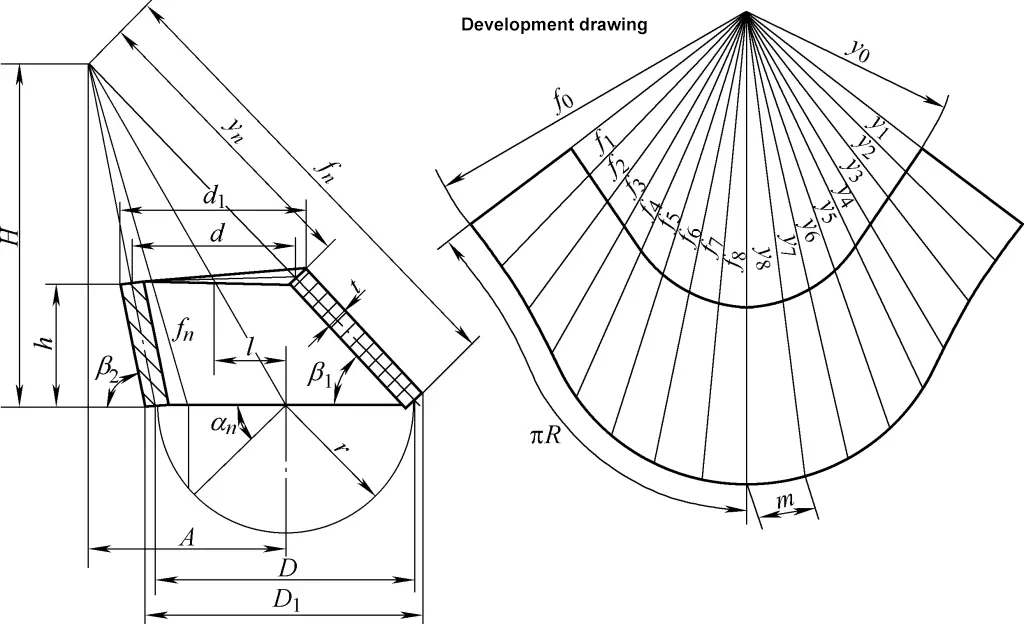
W formule
- D1, d1 - Średnice zewnętrzne dużych i małych końcówek (mm);
- D, d - Średnice środkowe dużego i małego końca (mm);
- h - wysokość środkowa (mm);
- l - Odległość mimośrodowa (mm);
- n - liczba podziałów na obwodzie; im większa liczba podziałów, tym bardziej skomplikowane obliczenia, ale tym dokładniejszy rysunek. Ogólnie liczbę podziałów można znaleźć w tabeli 1;
- fn, yn - Długości linii skośnych ukośnego prawego stożka kołowego (mm).
Tabela 1 Liczba oddziałów dla rozwoju blachy
| Promień rozwiniętego elementu/mm | Liczba dywizji |
| W ciągu 50 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| Ponad 2000 | 96 |
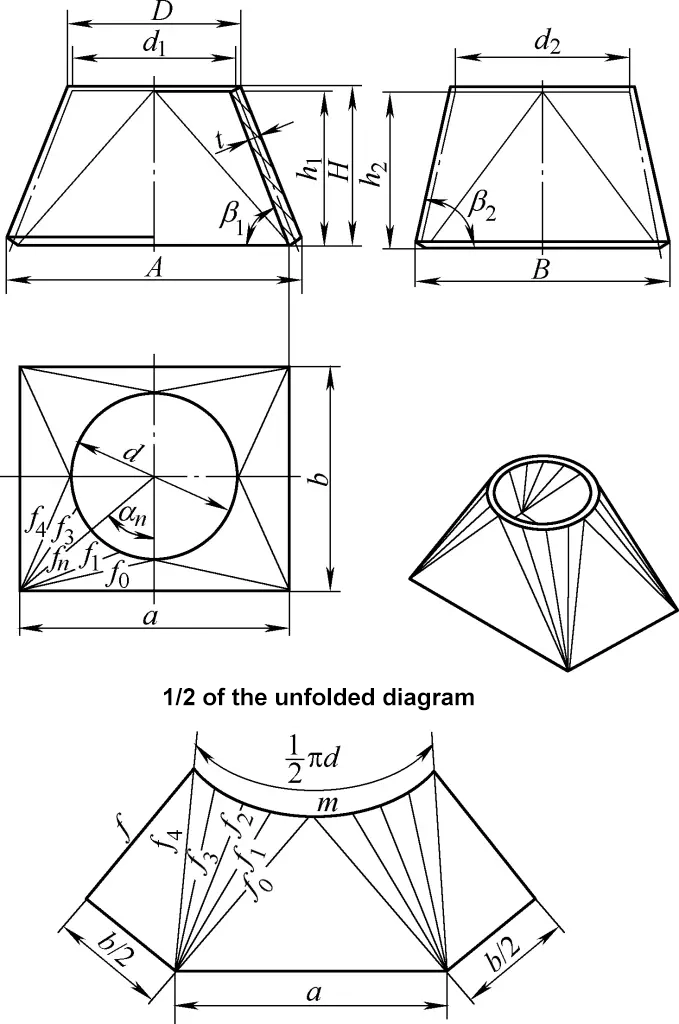
5. Obliczenia rozwojowe ortokonicznego prostokątnego do okrągłego kanału przejściowego
Ortokoniczny prostokątny do okrągłego kanał przejściowy pokazany na rysunku 5 składa się z czterech równych ukośnych powierzchni stożkowych i czterech symetrycznych trójkątnych płaszczyzn. Wzór obliczeniowy dla jego rysunku rozwinięcia jest następujący:
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(gdy 0<α<90°)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(gdy α=90°)
f=1/2√[(a-d)2+4h12]
m=πd/n
Znaczenie symboli we wzorze można znaleźć na rysunku 5, a n to liczba podziałów na obwodzie. Ogólnie rzecz biorąc, liczba podziałów w tabeli 1 może spełniać wymagania obliczeniowe.