Para peças de dobra de chapas metálicas, o cálculo do tamanho do blank é um pré-requisito para a formulação do plano do processo de dobra. Diferentes técnicos podem selecionar diferentes fatores de tolerância de dobra em seus documentos de processo, e a precisão do tamanho do blank afeta diretamente a precisão dimensional e a qualidade do produto das peças de dobra.
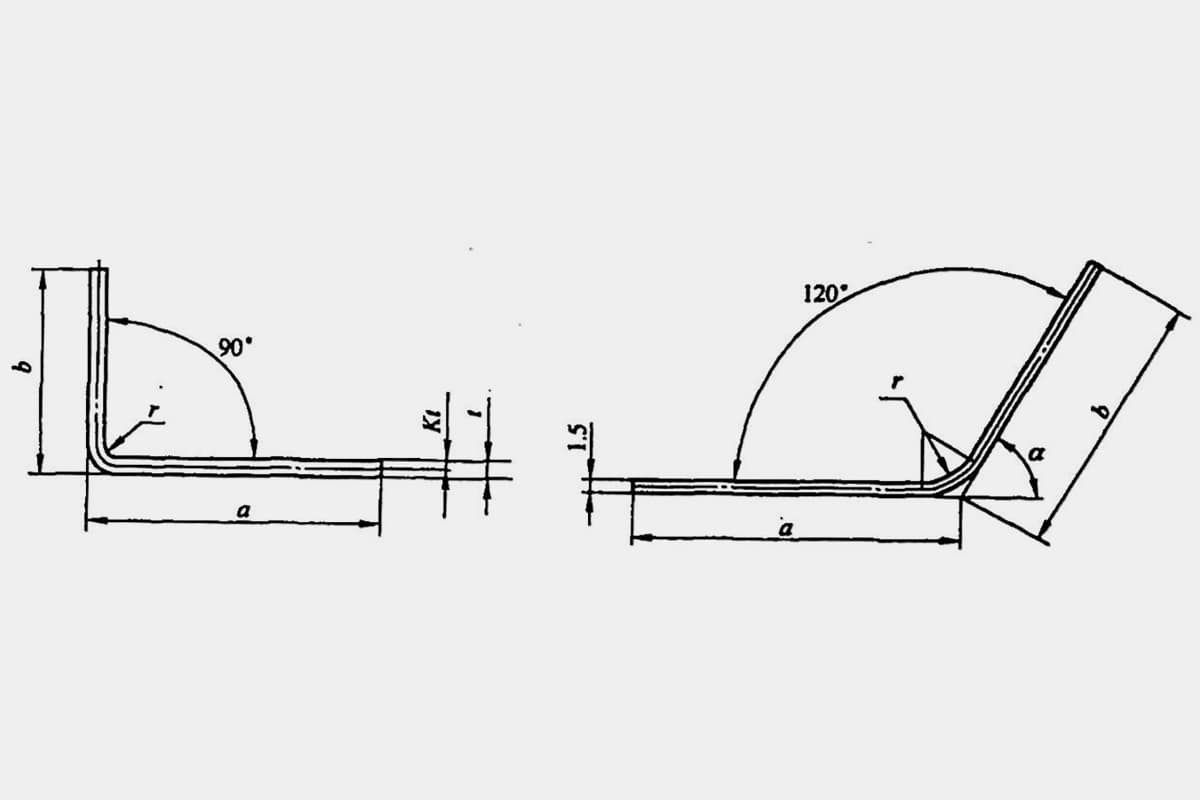
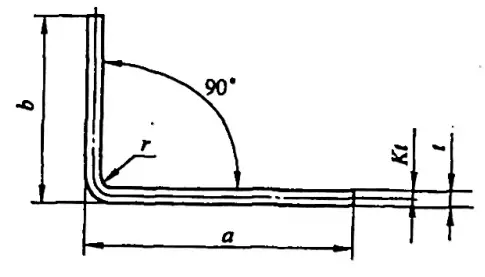
Às vezes, cálculos imprecisos podem até resultar em desperdício de produtos. O comprimento desdobrado L de uma peça típica de dobra simples (consulte a Figura 5-1) é L = a + b - y (em que y é a dedução de dobra, também conhecida como o valor de correção para a peça R).
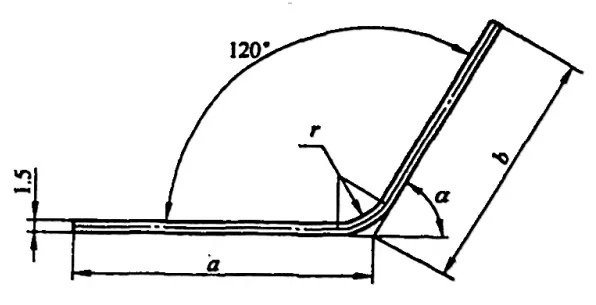
No entanto, em vários manuais e materiais, a dedução de flexão para φ=90° pode ser obtida diretamente, enquanto que para curvas que não sejam de 90°, como as mostradas na Figura 5-2, os técnicos precisam calculá-la com base em um fator de experiência (fator K).
Leitura relacionada: Explicação sobre a arte de desdobrar chapas metálicas
1. Princípio de cálculo da dimensão não dobrada de dobras de chapas metálicas
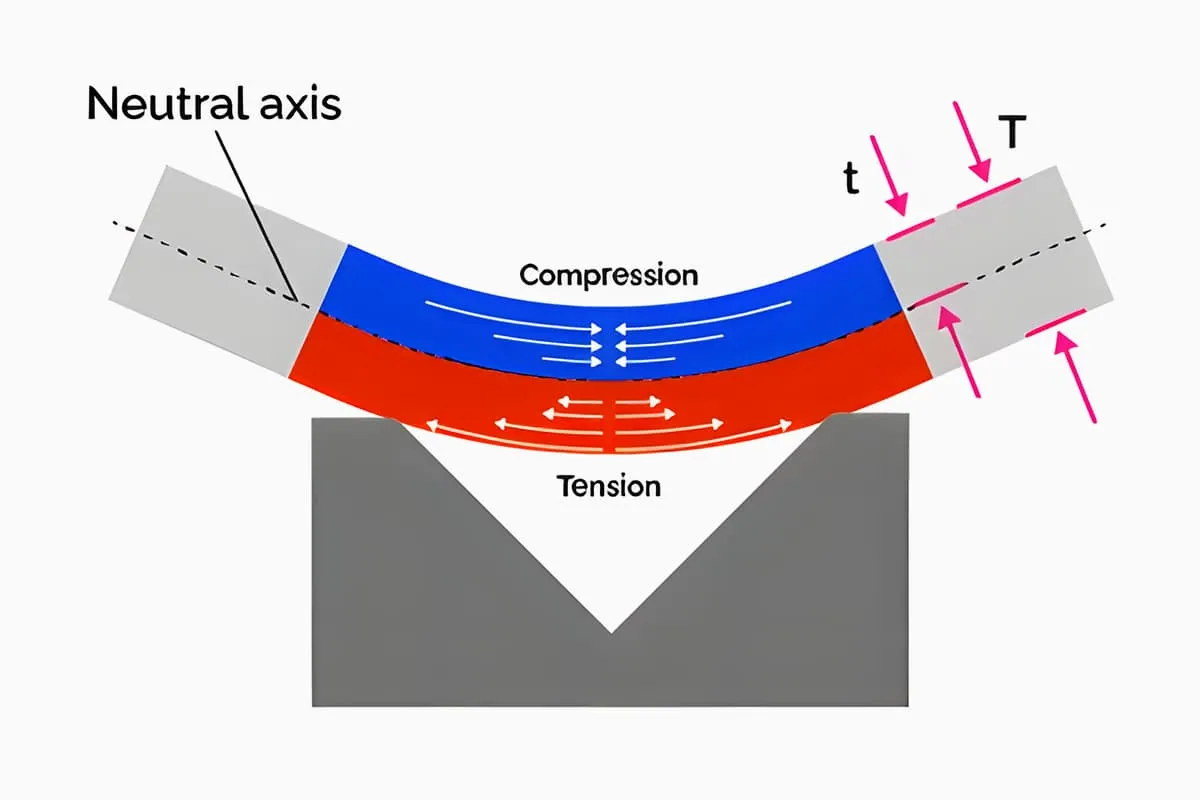
A dimensão desdobrada de um blank dobrado é determinada com base no princípio de que o comprimento da camada neutra permanece inalterado antes e depois da dobra. Quando a chapa metálica é dobrada, as fibras da camada externa da seção do blank são esticadas e as fibras da camada interna são comprimidas.
O alongamento das fibras da camada externa diminui gradualmente de fora para dentro, e a compressão das fibras da camada interna também diminui gradualmente de dentro para fora.
Quando as fibras passam do estiramento para a compressão ou da compressão para o estiramento, deve haver uma camada de fibras em que a tensão e a deformação são zero, e seu comprimento permanece inalterado antes e depois da flexão.
Essa camada é o que definimos como a camada neutra. Portanto, a chave para calcular a dimensão desdobrada da peça bruta dobrada é determinar a posição da camada neutra. A posição da camada neutra é determinada com base na condição de que o volume da peça dobrada e do blank sejam iguais antes e depois da deformação plástica.
2. Determinação do raio de curvatura ρ da camada neutra
Em teoria, devido à deformação desigual ao longo da direção da espessura da peça dobrada, a camada neutra é uma superfície parabólica, mas, para fins de cálculo, ela é normalmente considerada uma superfície de arco circular. Quando a deformação de flexão é muito pequena (r/t >6,5), a camada neutra pode ser considerada aproximadamente no meio da espessura do material, ou seja, o raio de curvatura da camada neutra é ρ=r+t/2.
Quando a deformação é muito grande (r/t≤6,5), a espessura do material se torna mais fina e a distorção da seção é muito grande, conforme mostrado na Figura 5-3.
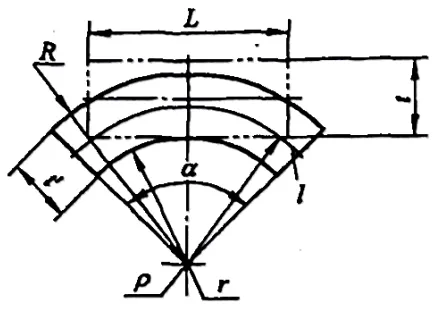
Nesse momento, para satisfazer a condição de equilíbrio de que a força resultante de todas as forças atuantes na seção seja zero, a camada neutra deve se mover em direção à superfície interna do material.
Nesse ponto, podemos determinar o raio de curvatura da camada neutra com base na condição de que o volume não se altere durante a deformação plástica, ou seja, o volume antes da flexão: V0=LBt, e o volume após a flexão:
V=(R2-r2)α*B'/2.
Na fórmula, B é a largura do blank (mm); B' é a largura média do blank após a dobra (mm); α é o ângulo central da dobra. De acordo com o princípio de que o volume é igual antes e depois da flexão, temos V0=V, isto é,
LBt=(R2-r2)α*B'/2, e L=(R2-r2)α*B'/2tB (5-1).
A partir da tensão e da deformação zero da camada neutra, obtemos L=l=αρ, em que L é o comprimento antes da deformação da camada neutra (mm) e l é o comprimento após a deformação da camada neutra (mm).
Substituindo a equação (5-1), obtemos ρ=(R2-r2)B'/2tB. Se substituirmos R=r+t' na equação acima, podemos obter outra forma da equação ρ=(r/t+η/2)tβη (5-2)onde β é o fator de largura, β=B'/B e, geralmente, quando uma placa larga (B>3t) é dobrada, considera-se que β=1; η é o fator de afinamento, η=t'/t.
A equação (5-2) é a fórmula para calcular teoricamente a posição da camada neutra. Ao fazer o cálculo, precisamos saber η, ou seja, a regra de afinamento. O valor de η pode ser consultado na Tabela 5-1.
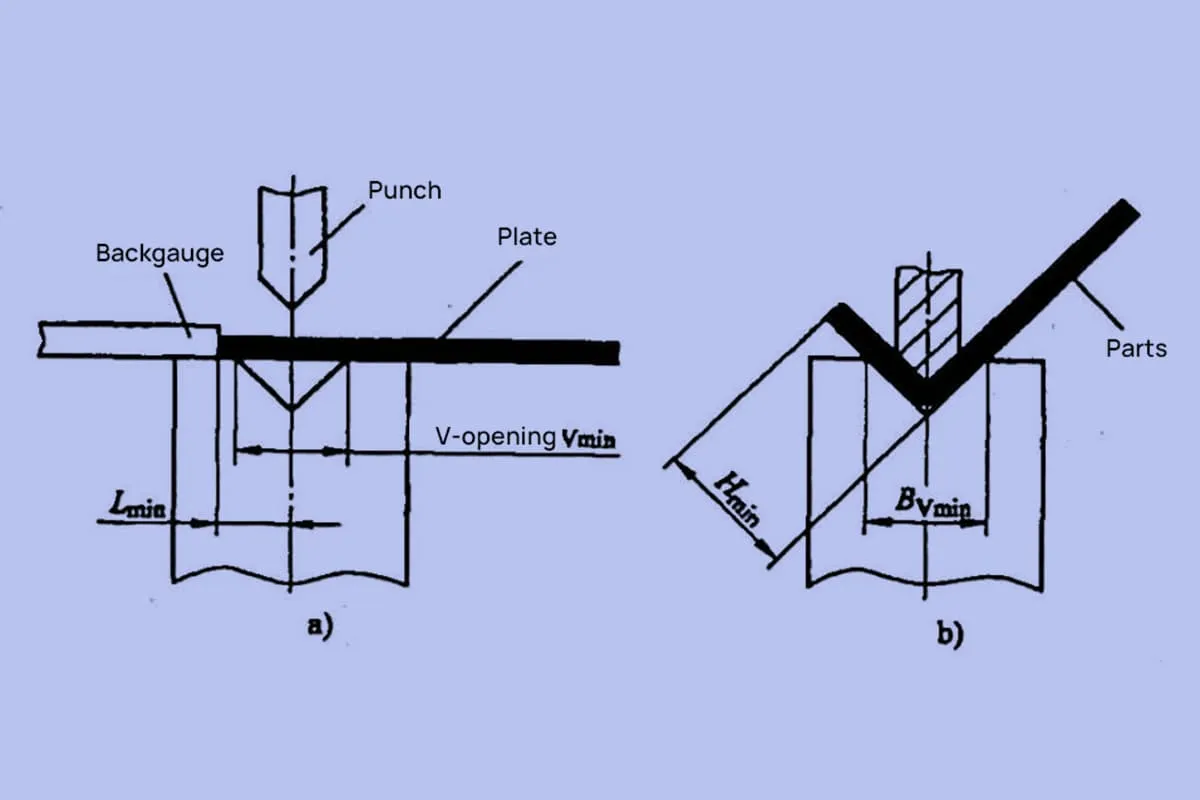
Deve-se ressaltar que a regra de desbaste é bastante complexa, a distribuição da posição da camada neutra na área de dobra não é uniforme e a regra de desbaste também está relacionada a muitos fatores, como o método de dobra, a largura da ranhura da matriz inferior de dobra e a espessura do material.
Isso traz erros inevitáveis para o cálculo teórico da posição da camada neutra, reduzindo assim o valor da aplicação prática do método de determinação teórica.
Tabela 5-1: Fator de desbaste η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
Na produção real, uma fórmula empírica, que é mais simples do que o cálculo teórico, é normalmente usada para determinar a posição do eixo neutro, como segue:
ρ = r + Kt (5-3)
Onde:
- ρ - Raio de curvatura do eixo neutro (mm)
- r - Raio interno de flexão da matéria-prima (mm)
- t - Espessura do material (mm)
- K - Coeficiente do eixo neutro (empírico) Fator K), consulte a Tabela 5-2
Tabela 5-2: Valores empíricos do coeficiente de eixo neutro K
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
Observação:
- K1 é aplicável a curvas em forma de V ou U com uma placa superior ou placa de pressão.
- K2 é adequado para curvas em forma de V sem placa superior.
3. Cálculo das dimensões não dobradas do blank para várias dobras típicas de chapas metálicas
Com base na definição da camada neutra, a dimensão desdobrada do blank deve ser igual ao comprimento da camada neutra. Normalmente, com base na dimensão interna raio de curvatura r do blank, as dobras são categorizadas como dobras com cantos arredondados e não arredondados: as dobras são consideradas com cantos arredondados quando r>0,5t e não arredondadas quando r<0,5t.
Além disso, com base na largura da placa B, as dobras são categorizadas em dobras de placa larga e estreita: quando a largura da placa B>3t, ela é chamada de dobra de placa larga, e quando a largura da placa B<3t, ela é chamada de dobra de placa estreita.
Na prática de produção, as dobras com raio de canto redondo (r>0,5t) e placas largas (B>3t) são as mais usadas e, considerando a universalidade das dobras, discutiremos principalmente o cálculo das dimensões desdobradas do blank para dobras com raio de canto redondo e placas largas durante a dobra.
3.1 Cálculo das dimensões não dobradas em branco para curvas de canto redondo (r>0,5t)
Quando r>0,5t, B>3t, devido ao afinamento da parte dobrada não ser grave e a distorção da seção transversal ser pequena, o comprimento da peça bruta pode ser determinado com base no princípio de que o comprimento da camada neutra é igual à dimensão desdobrada da peça bruta.
Os métodos comuns para calcular as dimensões desdobradas do blank de curvas de canto redondo (r>0,5t) são divididos em: cálculo do coeficiente de flexão e cálculo do valor de dedução de flexão.
1. Curvas com cantos arredondados (r>0,5t) Cálculo do coeficiente de curvatura para dimensões não dobradas em branco:
1) O coeficiente de flexão é o comprimento da parte do arco medido ao longo da camada neutra da zona de deformação de flexão (parte R de flexão), conforme mostrado na Figura 5-4.
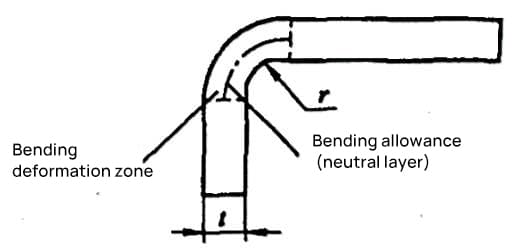
O coeficiente de flexão é calculado pela fórmula (5-4): x=παρ/180° (5-4)
Onde ρ é o raio de curvatura da camada neutra (mm).
2) A Figura 5-5 mostra um exemplo de notação de dimensão para o cálculo do coeficiente de flexão das dimensões desdobradas do blank, e sua fórmula para calcular o coeficiente de flexão das dimensões desdobradas do blank é a seguinte.

a) φ > 90° b) φ≤90
L=a+b+x (5-5)
Substituindo a equação (5-3) pela equação (5-4), obtemos a fórmula para o coeficiente de flexão:
x=πα(r+Kt)/180° (5-6)
Substituindo a equação (5-6) pela equação (5-5), obtemos a fórmula para calcular o tamanho desdobrado do blank dobrado:
L=a+b+πα(r+Kt)/180° (5-7)
Onde:
- L - O tamanho desdobrado do espaço em branco (mm);
- K - Coeficiente para o fator K, consulte a Tabela 5-2 para obter o valor;
- α - O ângulo central de flexão, sua relação com o ângulo da parte flexionada é α=180°-φ;
- r - O raio de curvatura da camada interna da peça bruta (mm);
- t - A espessura do material (mm);
- a, b - Os comprimentos das partes retas do componente (mm), respectivamente.
2. Cálculo da dedução de flexão para o tamanho desdobrado de uma peça dobrada com canto arredondado (r>0,5t)
1) A dedução de dobra (também conhecida como valor de correção para a parte R) é a diferença entre duas vezes o R da zona de deformação de dobra (a parte R da dobra) e o coeficiente de dobra, conforme mostrado na Figura 5-6.

A dedução de flexão (valor de correção para a parte R) é calculada de acordo com a equação (5-8):
y = 2R-παr/180° (5-8)
2) A Figura 5-7 mostra um exemplo de anotação de dimensão para o cálculo da dedução de flexão para o tamanho desdobrado da peça bruta. A dedução de flexão y é calculada pela seguinte fórmula:
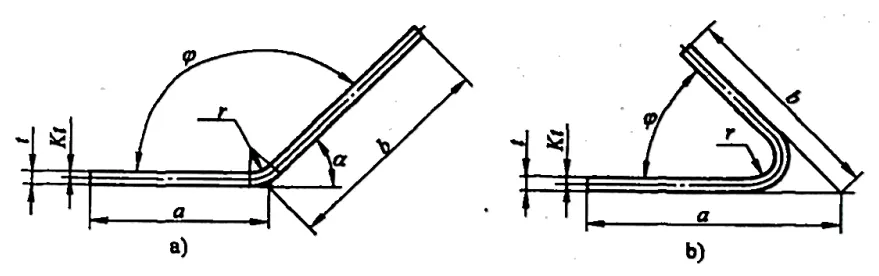
a)90°<φ≤165° b)φ≤90°
①Quando φ ≤ 90°:
R=(r+t)/tan(φ/2)
Substituindo a fórmula acima e a fórmula (5-3) pela fórmula (5-8), obtemos a dedução de curvatura (ou seja, o valor de correção da parte R) para uma curvatura φ≤90° (consulte a Figura 5-7b):
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
②Quando 90°<φ≤165°:
R=(r+t)tan[(180°-φ)/2]
Substituindo a fórmula acima e a fórmula (5-3) pela fórmula (5-8), obtemos a dedução de curvatura (ou seja, o valor de correção da parte R) para uma curvatura de 90°<φ≤165° (consulte a Figura 5-7a):
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
③Quando 165°<φ≤180°:
y≈0
3) A fórmula para calcular o valor da dedução de flexão do tamanho do blank da peça mostrada na Figura 5-7 é a seguinte:
L=a+b-y (5-11)
①Quando φ≤90°, substituindo a fórmula (5-9) pela fórmula (5-11), obtemos a fórmula para calcular o valor de dedução de flexão do tamanho do espaço em branco da seguinte forma:
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
②Quando 90°<φ≤165°, substituindo a fórmula (5-10) pela fórmula (5-11), obtemos a fórmula para calcular o valor de dedução de flexão do tamanho do blank da seguinte forma:
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
③Quando 165°<φ≤180°:
L≈a+b (5-14)
Onde,
- y - Dedução de flexão (mm)
- L - Tamanho da peça em branco (mm)
- r - Raio de curvatura interno da peça bruta (mm)
- t - Espessura do material (mm)
- α - Ângulo do centro de curvatura, sua relação com o ângulo de curvatura é α=180°-φ
- a, b-Comprimentos das bordas da peça (mm) até o vértice de flexão.
3. Cálculo do tamanho do blank para curvas de múltiplos ângulos
Para curvas de vários ângulos, o tamanho do blank é a soma da parte R e dos comprimentos das bordas retas.
1) Cálculo do tamanho do blank de dobra multiangular pelo coeficiente de dobra:
L=l1+l2+...+ln+1+nx (5-15)
Onde l1, l2...ln+1 são os comprimentos das partes retas de cada borda da peça (mm);
n é o número de curvas R.
2) Cálculo do tamanho do blank de dobra multiangular pela dedução de dobra:
L=l1+l2+...+ln+1-ny (5-16)
Onde l1, l2...ln+1 são os comprimentos das bordas da peça (mm) até o vértice de flexão;
n é o número de curvas R.
Exemplo 5-1: Calcule o tamanho do blank para a curva mostrada na Figura 5-8.
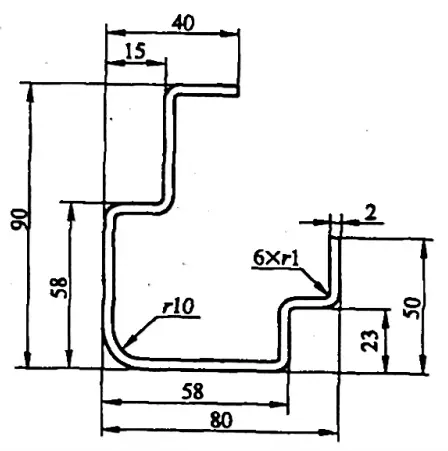
Solução 1: Calcule o tamanho do blank usando o coeficiente de flexão.
Consulte o Apêndice A: Quando o ângulo de flexão da peça φ=90°, a espessura t=2 mm e o raio r=10 mm, o coeficiente de flexão é de 2,68 mm;
Quando o ângulo da peça de flexão é de 90°, a espessura t=2 mm e o raio r=10 mm, o coeficiente de flexão é x2=16,9 mm.
A partir das equações (5-5) e (5-15), o tamanho plano da peça bruta para a peça dobrada é calculado como:
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2,68 + 16,9]mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240,98 mm.
Solução 2: Calcule o tamanho plano da peça bruta usando o valor de dedução de dobra.
Consulte o Apêndice C: Para uma curva com ângulo φ=90°, espessura t=2 mm e raio r=1 mm, o valor de correção para a seção R é y1=3,32 mm; para uma curva com ângulo φ=90°, espessura t=2 mm e raio r=10 mm, o valor de correção para a seção R é y2=7,1 mm.
O tamanho bruto da peça dobrada pode ser obtido pelas equações (5-11) e (5-16):
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3,32 - 7,1] mm
= (25+34+17+116+25+24+27-19,92-7,1) mm
= 240,98 mm
Exemplo 5-2: Calcule o tamanho bruto da peça dobrada mostrada na Figura 5-9.
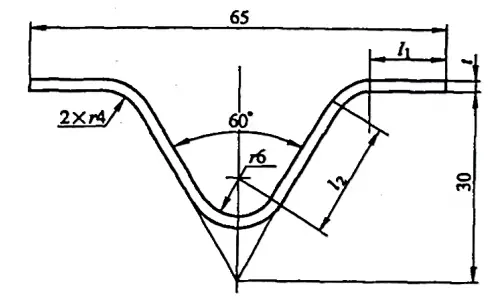
Solução: Calcule o tamanho bruto usando o coeficiente de flexão.
A fórmula para calcular as dimensões do blank da peça dobrada a partir das equações (5-5) e (5-15) é:
L=2l1+2l2+2x1+x2
onde l1 = [32,5 - (30tan30°+4tan30°)] mm = 12,87 mm
e l2 = [(30/cos30°) - (8/tan30°+4tan30°)] mm = 18,47 mm
Referência ao Apêndice A: quando o ângulo de curvatura φ=120°, t=2mm, r=4mm, o valor do fator de curvatura é x1=4,98mm; quando o ângulo de curvatura φ=60°, t=2mm, r=6mm, o valor do fator de curvatura é x2=14,16 mm.
Substituindo esses valores na fórmula, obtém-se o comprimento desdobrado do blank como L= (2×12,87 + 2×18,47 + 2×4,98 + 14,16) mm = 86,8 mm.
Deve-se observar que, para curvas mais simples com requisitos de menor precisão, as dimensões desdobradas do blank podem ser calculadas diretamente. No entanto, para curvas mais complexas ou com requisitos de precisão mais altos, o formato e as dimensões do blank desdobrado precisam ser testados repetidamente e revisados continuamente para confirmar o formato e as dimensões do blank.
3.2 Cálculo das dimensões de desenvolvimento do blank para componentes de curvatura acentuada (r<0,5t)
Quando o raio de curvatura r de um componente é menor que 0,5t, ele é chamado de curvatura acentuada. O cálculo da dimensão de desenvolvimento do blank para esses componentes é baseado no princípio da consistência do volume antes e depois da dobra.
Com curvas acentuadas, devido ao forte afinamento do material na curva, o processo de deformação é extremamente complexo, dificultando o cálculo preciso das dimensões de desenvolvimento do blank. Portanto, as dimensões de desenvolvimento do blank calculadas precisam ser corrigidas com base em dados empíricos ou por meio de flexão experimental.
A fórmula de cálculo para as dimensões de desenvolvimento do blank de componentes de curvatura acentuada (r<0,5t, φ=90°) pode ser encontrada na Tabela 5-3.
Tabela 5-3 Fórmula de cálculo para as dimensões de desenvolvimento do blank de componentes de curvatura acentuada (r<0,5t, φ=90°) (unidade: mm)
| Número de série | Recursos de flexão | Esquema | Fórmula |
| 1 | Dobre um canto. |  | L=a+b+0,4t |
| 2 | Achate-o. |  | L=a+b-0,43t |
| 3 | Dobre dois cantos de uma vez. | 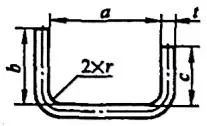 | L=a+b+c+0,6t |
| 4 | Dobre três cantos simultaneamente. | 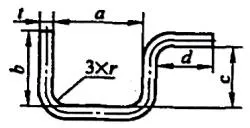 | L=a+b+c+d+0,75t |
| 5 | Dobre dois cantos na primeira instância e dobre outro canto na segunda. | L=a+b+c+d+t | |
| 6 | Dobre quatro cantos ao mesmo tempo. | 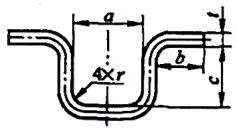 | L=a+2b+2c+1,2t |
| 7 | Dobre para formar quatro cantos em duas instâncias. | L=a+2b+2c+1,2t |
3.3 Cálculo das dimensões não dobradas para peças dobradas do tipo dobradiça
Para o tipo dobradiça peças de dobra com r= (0,6~3,5)t (consulte a Figura 5-10), o processo de flangeamento geralmente segue o padrão mostrado na Figura 5-11. Durante o flangeamento, a espessura da chapa metálica aumenta e a camada neutra se desloca para fora. As dimensões desdobradas do blank podem ser calculadas de forma aproximada pela seguinte fórmula:
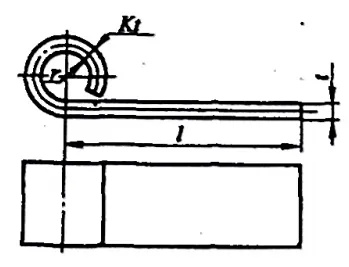
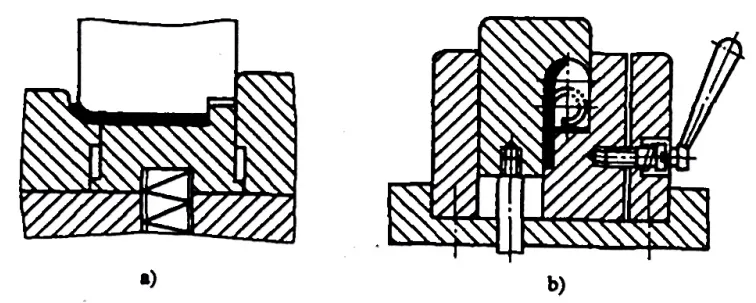
- a) Primeira operação
- b) Segunda operação
L=l+1,57π(r+Kt)+r
Onde:
- L - Dimensões desdobradas da folha em branco (mm);
- l - Comprimento do segmento reto (mm);
- r - Raio de curvatura interno da peça bruta (mm);
- K - Coeficiente de deslocamento da camada neutra. Quando r/t=0,5~1,8, K é normalmente considerado como 0,5~0,70 (quanto menor o valor de r/t, maior o valor de K; inversamente, menor o valor de K). Ele também pode ser selecionado de acordo com a Tabela 5-4.
Tabela 5-4 Coeficiente de deslocamento da camada neutra para peças de flexão do tipo dobradiça
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |