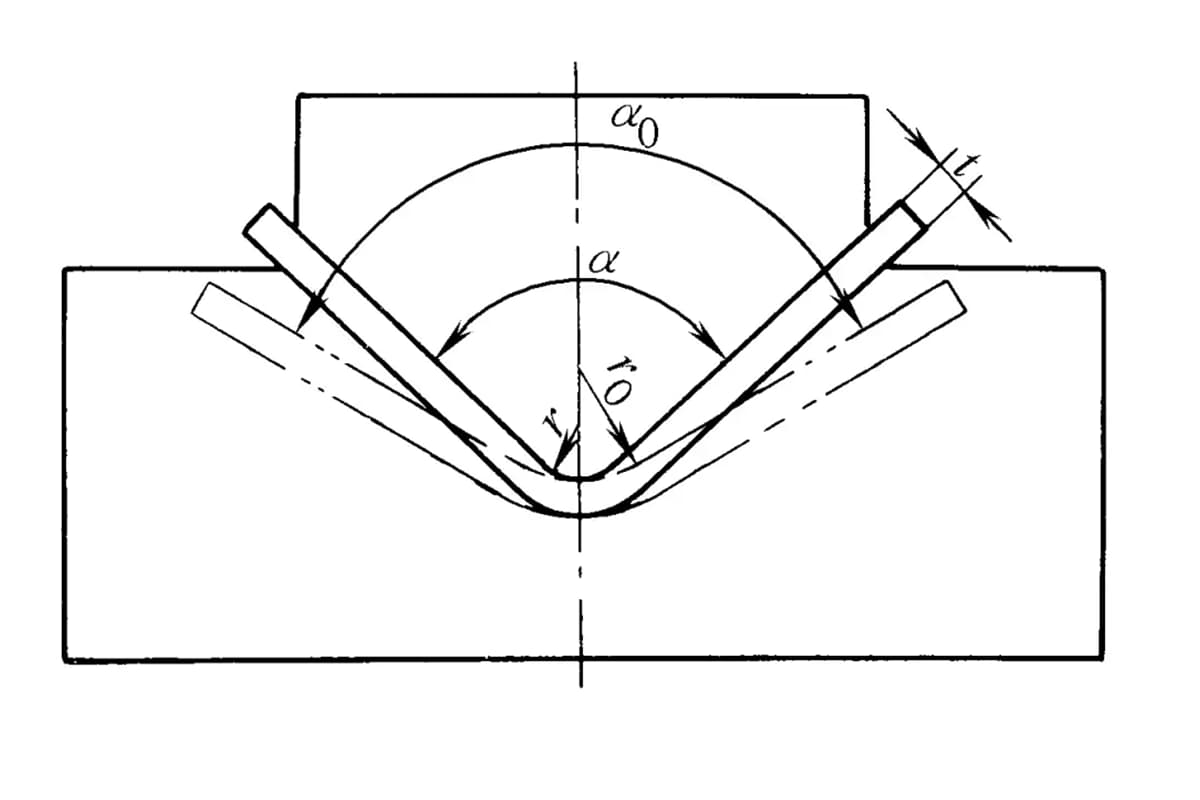
Conforme mencionado anteriormente, a deformação plástica e a deformação elástica coexistem durante a flexão e, depois que a carga externa é removida, a peça de trabalho se recupera, tornando suas dimensões inconsistentes com as dimensões do molde (consulte a Figura 1).
O retorno elástico é geralmente representado pela mudança no ângulo: ao dobrar com um grande raio de curvatura, além de calcular o ângulo de retorno elástico, também é necessário calcular a mudança no raio de dobra.
I. Principais fatores que afetam o retorno elástico
1. Propriedades mecânicas do material
Quanto maior a resistência ao escoamento σ s quanto menor for o módulo de elasticidade E e quanto mais intenso for o endurecimento por trabalho (valores mais altos de k e n), maior será o retorno elástico.
2. Raio de curvatura relativo r/t
Quando r/t é pequeno, a deformação tangencial geral na superfície externa da placa de flexão é grande. Embora o valor numérico da deformação elástica também aumente, a proporção da deformação elástica na deformação total diminui. Portanto, a proporção de ângulo de retorno elástico em relação à flexão ângulo △α/α e a relação entre o retorno elástico da curvatura e o raio de curvatura △ρ/ρ diminuem à medida que o raio de curvatura diminui.
3. Ângulo de flexão α
Quanto maior o ângulo de flexão α, mais longa será a zona de deformação e, portanto, maior será o ângulo de retorno elástico, mas isso não afeta o retorno do raio de curvatura.
4. Métodos de dobra e estruturas de matrizes
Diferentes métodos de dobra e estruturas de matriz têm um impacto significativo sobre o processo de dobra, as condições de tensão e a influência sobre as áreas deformadas e não deformadas do blank, portanto, os valores de springback também variam.
5. Força de flexão
Na produção real, os métodos de flexão com um determinado componente de correção são frequentemente usados, permitindo que a prensa exerça uma força maior do que a necessária para a deformação por flexão. Nesse momento, o estado de tensão e a natureza da deformação na área de deformação por flexão apresentam certas diferenças em relação à flexão pura e, quanto maior a força aplicada, mais significativa é essa diferença. Quando a força de correção é muito grande, ela pode mudar completamente a natureza do estado de tensão na área de deformação em branco e fazer com que a área sem deformação também se torne uma área de deformação.
6. Atrito
O atrito entre a superfície do blank de dobra e a superfície da matriz pode alterar o estado de estresse de várias partes do blank de dobra, especialmente ao dobrar em várias partes com diferentes curvaturas, o impacto do atrito é mais significativo.
Em geral, acredita-se que o atrito pode aumentar a tensão de tração na área de deformação por flexão na maioria dos casos, tornando o formato da peça mais próximo ao da matriz. Entretanto, durante a flexão por estiramento, o impacto do atrito costuma ser adverso.
7. Desvio de espessura
Se houver um grande desvio de espessura no blank, para uma determinada matriz, a folga de trabalho real varia e, portanto, o valor do retorno elástico também flutua.
II. Cálculo aproximado
Na flexão livre, a fórmula simplificada para estimar o ângulo de retorno elástico é mostrada na Tabela 1.
Tabela 1 Fórmula aproximada para calcular o ângulo de retorno elástico em flexão livre
| Método de flexão | Fórmula de cálculo do ângulo de retorno elástico β (lado único) |
| Dobra de peças em forma de V | tanβ = 0. 375l/Kt-σs/E |
| Dobra de peças em forma de U | tanβ = 0,375l1/Kt-σs/E |
Observação:
K---coeficiente, determinado pela posição da camada neutra;
l--distância do ponto de apoio, ou seja, a largura da abertura da matriz;
l 1 ---Braço da alavanca de flexão, l 1 = rsoco + rmorrer + 1.25t.
Na dobra com uma almofada de pressão, o valor do retorno elástico não depende apenas dos valores de r/t, l/t e α, mas também do ajuste da prensa e do grau de endurecimento por trabalho a frio do metal.
III. Dados empíricos
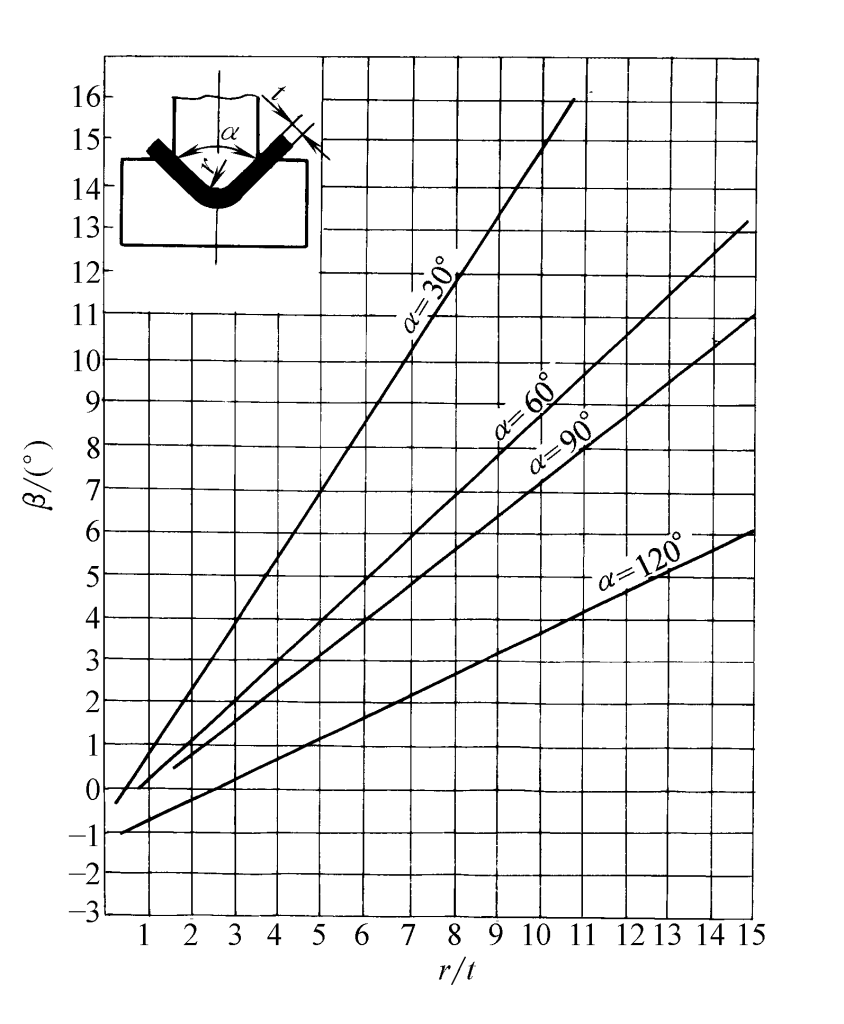
Para placas de aço carbono submetidas à flexão em V, a relação entre o ângulo de retorno elástico β e r/t é mostrada nas Figuras 2 a 5.
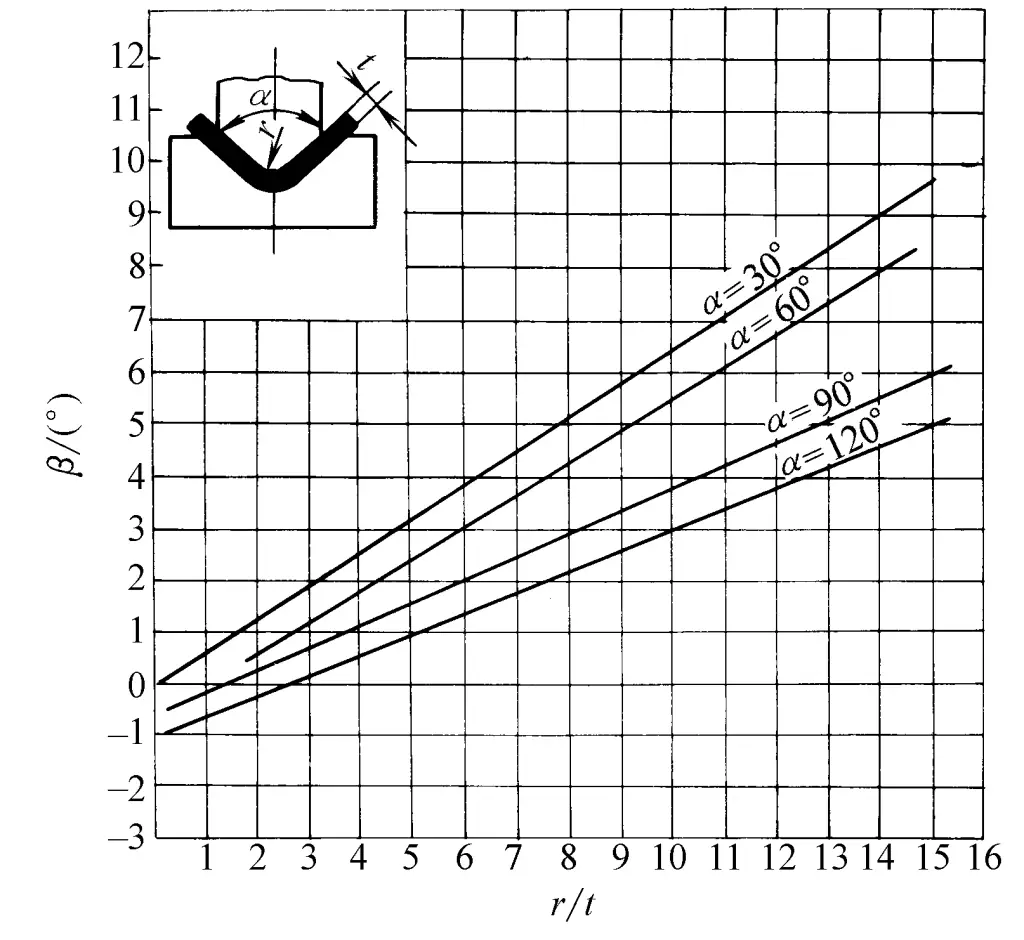
- Quando α = 30°, β = 0,75r/ t -0,39
- Quando α = 60°, β = 0,58r/ t -0,80
- Quando α = 90°, β = 0,43r/ t -0,61
- Quando α = 120°, β = 0,36r/ t -1. 26
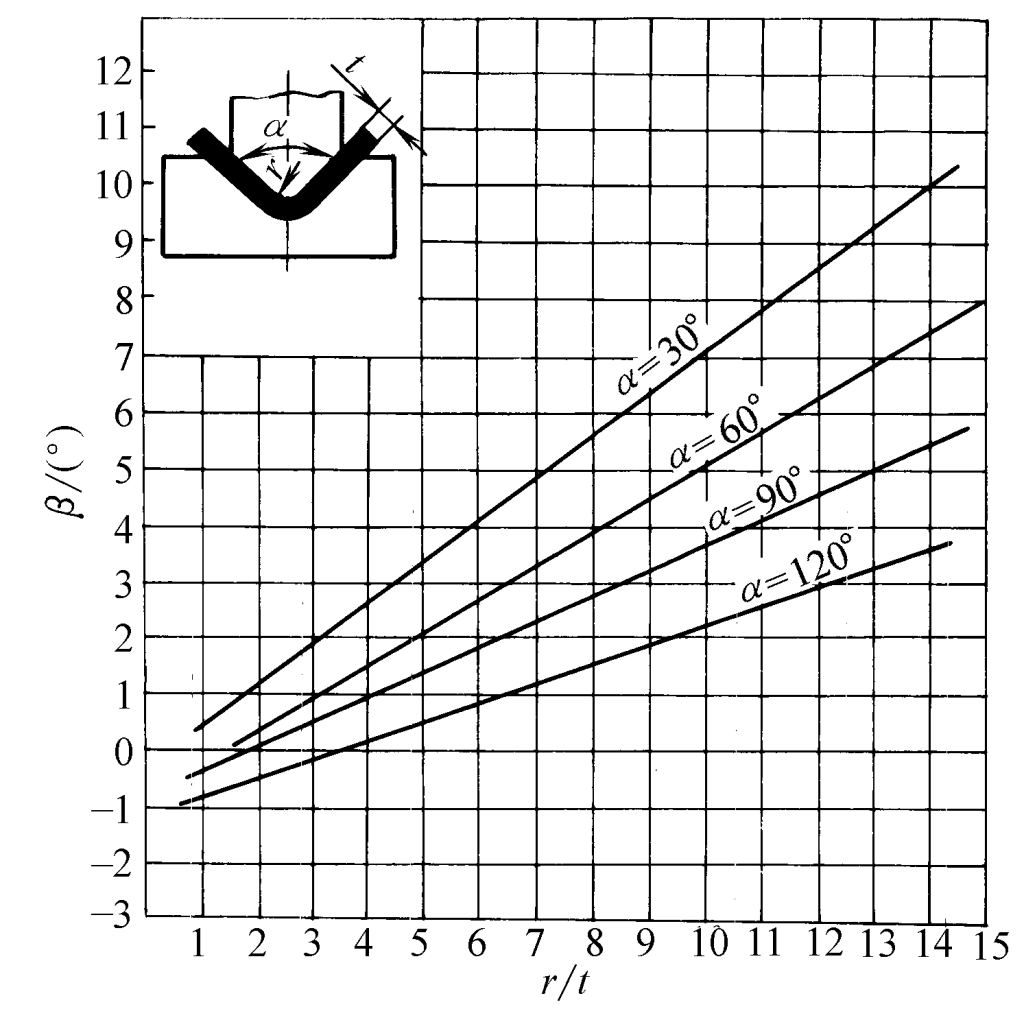
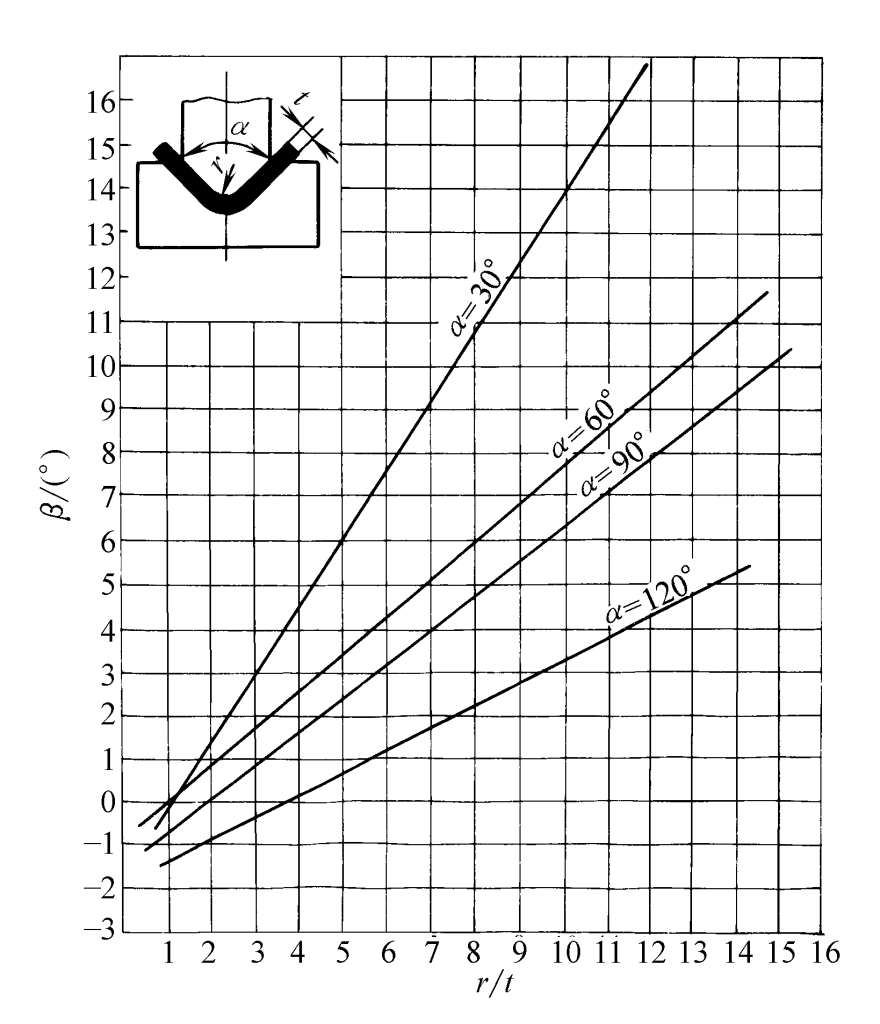
- Quando α = 30°, β = 0,69r/t -0,23
- Quando α = 60°, β = 0,64r/t -0,65
- Quando α = 90°, β = 0,434r/t -0,36
- Quando α = 120°, β = 0,37r/t -0,58
- Quando α = 30°, β = 1,59r/t -1,03
- Quando α = 60°, β = 0,95r/t -0,94
- Quando α = 90°, β = 0,78r/t -0,79
- Quando α = 120°, β = 0,46r/t -1,36
- Quando α = 30°, β = 1,51r/t -1,48
- Quando α = 60°, β = 0,84r/t -0,76
- Quando α = 90°, β = 0,79r/t -1,62
- Quando α = 120°, β = 0,51r/t -1,71
IV. Principais medidas para reduzir o retorno elástico
1. Em condições próximas à flexão pura, as correções necessárias podem ser feitas no formato da parte de trabalho do molde de flexão com base no cálculo dos valores de retorno elástico ou em dados empíricos.
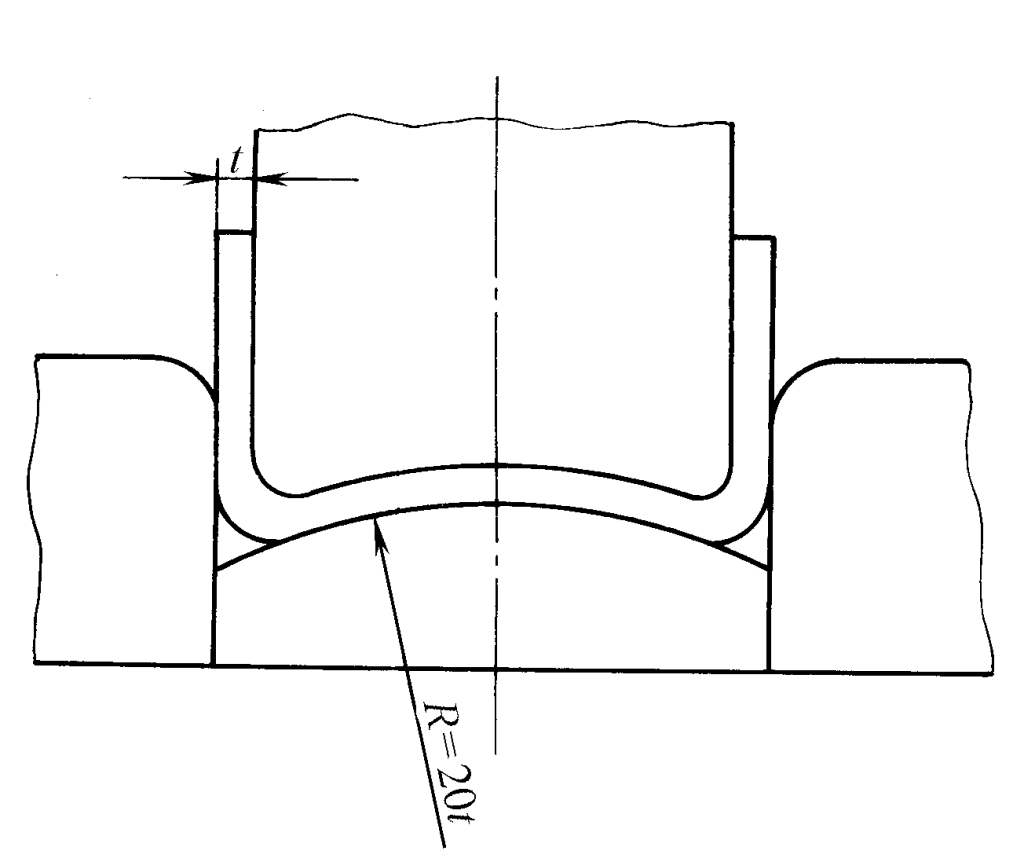
2. Ao utilizar o padrão de que diferentes partes da peça bruta dobrada têm diferentes direções de retorno elástico, vários fatores de influência (raio do canto arredondado do molde, folga, largura da abertura, força de correção, força de pressão etc.) podem ser ajustados adequadamente para cancelar o retorno elástico em direções opostas. Conforme mostrado na Figura 6, o retorno elástico gerado na parte inferior da peça é usado para compensar o retorno elástico nos dois cantos arredondados.
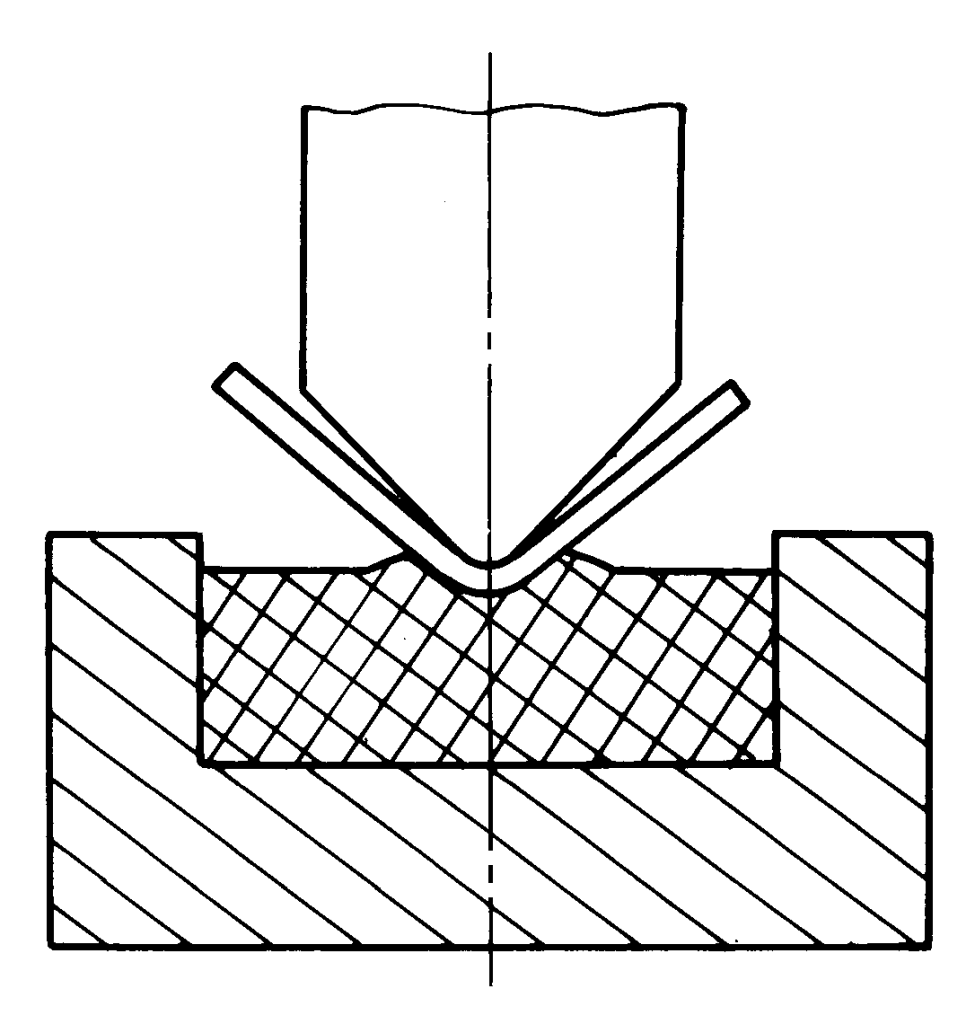
3. Use um molde côncavo macio feito de borracha de poliuretano em vez de um molde côncavo de metal rígido para dobrar, conforme mostrado na Figura 7.
4. Faça o punção de dobra ou a placa de prensagem em um formato com saliências locais ou reduza a folga do molde nos cantos arredondados, de modo que a força de perfuração está concentrado na área de deformação por flexão que causa o retorno elástico, alterando seu estado de tensão, conforme mostrado na Figura 8.
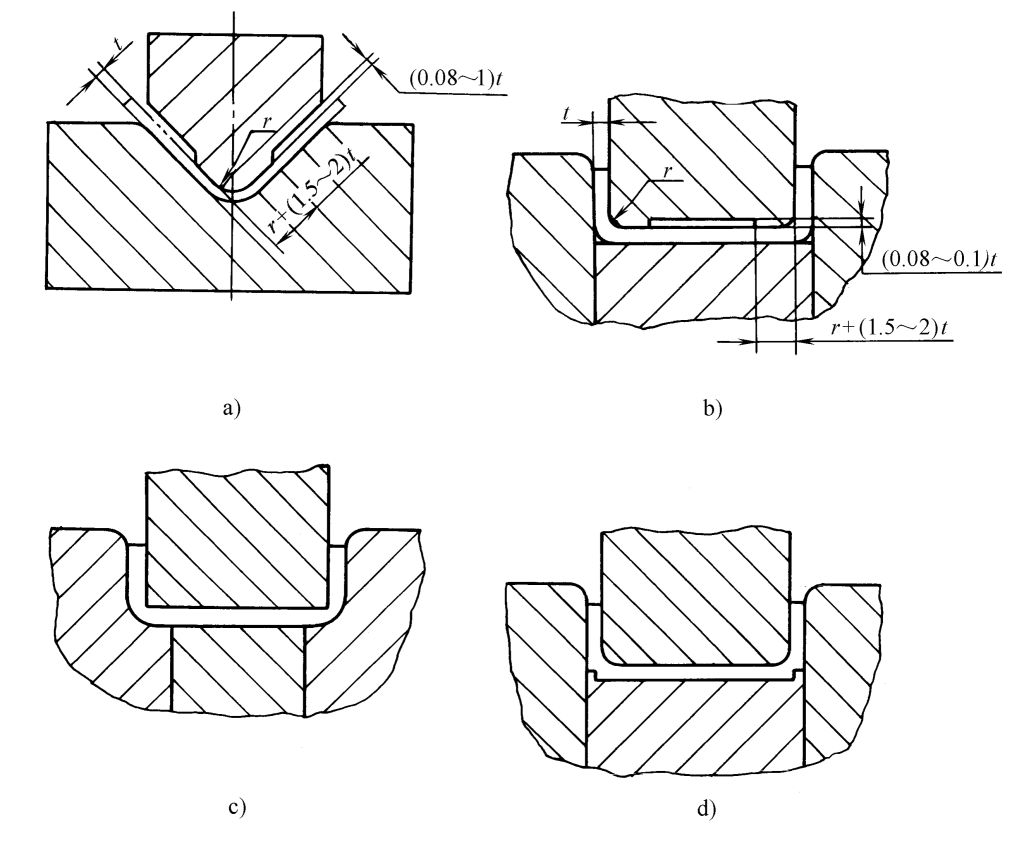
5. Use uma estrutura de molde côncava com um bloco oscilante, conforme mostrado na Figura 9.
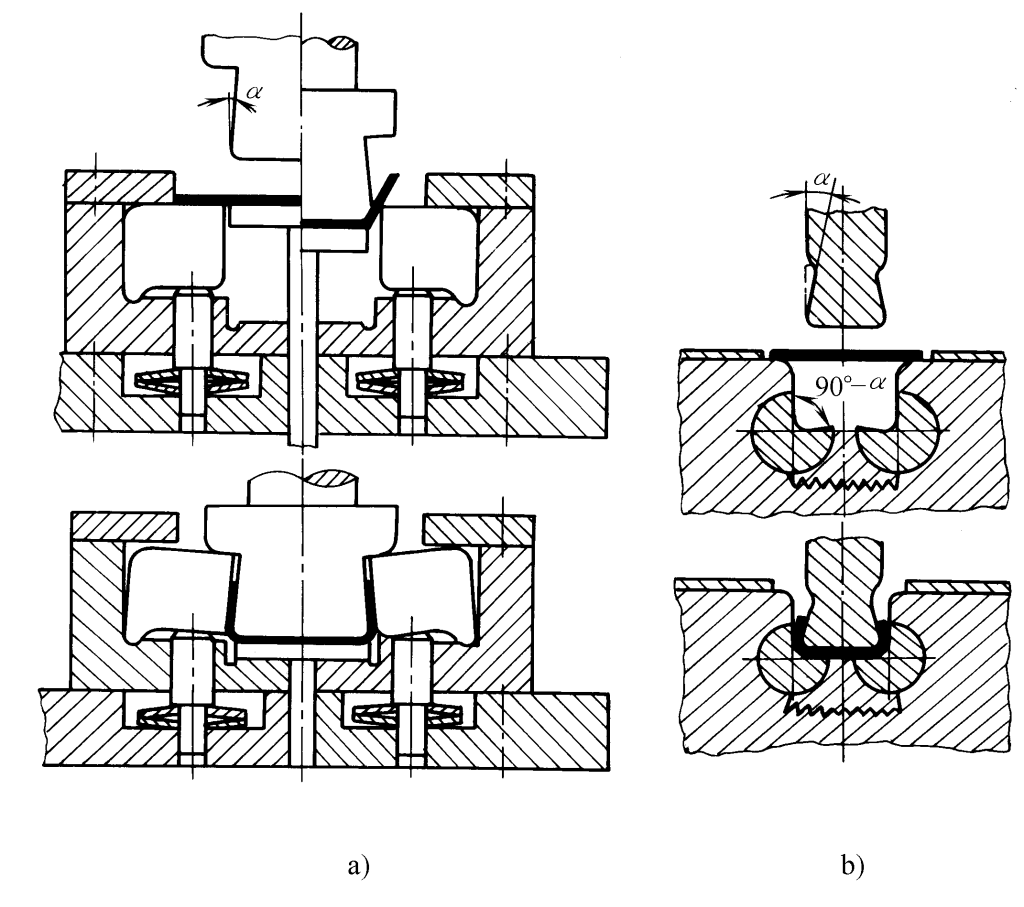
6. Use o método de prensagem longitudinal, após a conclusão do processo de dobra, use o ombro saliente do molde para pressionar longitudinalmente o blank de dobra, fazendo com que todas as tensões na seção transversal do blank na área de deformação da dobra se tornem tensões compressivas, conforme mostrado na Figura 10.
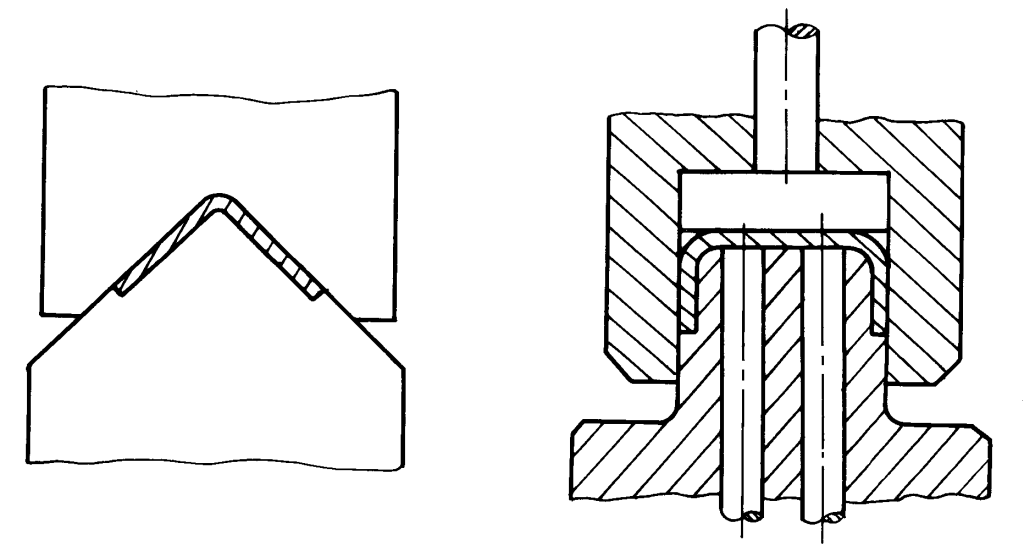
7. Use o método de dobragem por tração, principalmente para peças com grande comprimento e raio de curvatura.
8. Use métodos para melhorar a rigidez estrutural das peças, conforme mostrado nas Figuras 11 a 14.