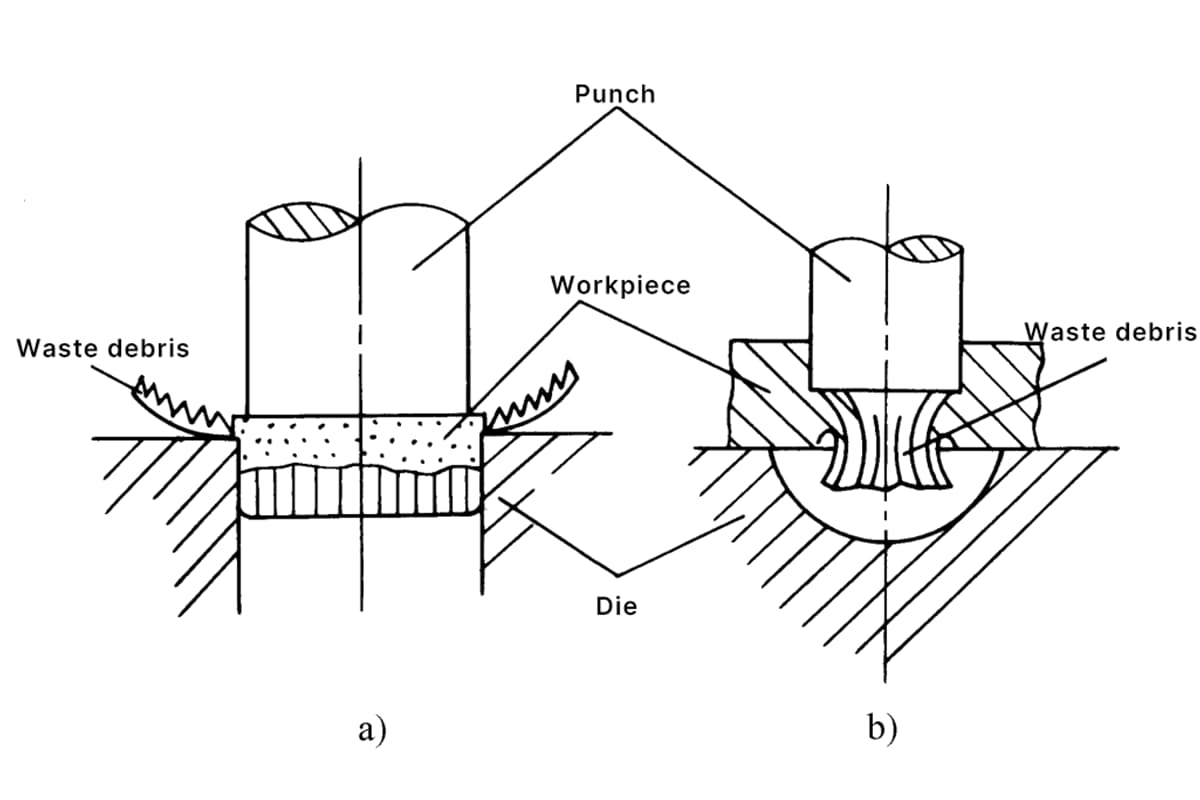
A força de perfuração inclui força de bloqueioA força de perfuração é calculada com base na força de perfuração, na força de remoção, na força de empurrão e na força de elevação. O cálculo da força de perfuração é fundamental para a seleção da prensa correta, conforme mostrado na Figura 1.
Força de bloqueio
onde:
- F - a força de bloqueio (N);
- L - o comprimento do perímetro da peça bruta (mm);
- t - a espessura do material (mm);
- r - a resistência ao cisalhamento do material (MPa).
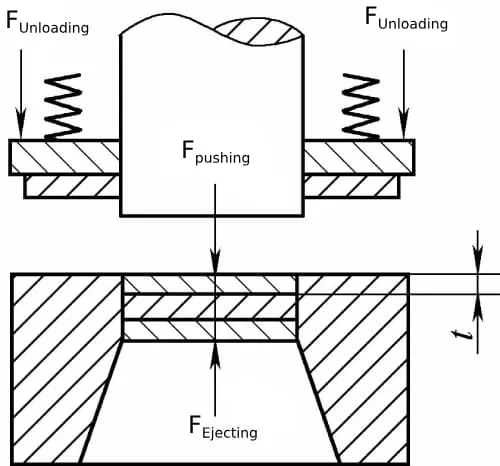
Força de remoção, força de empurrão, força de elevação
a) A força de remoção é a força necessária para remover o material preso no punção, dada por
Fdescarregamento = kdescarregamento * F
b) A força de empuxo é a força necessária para empurrar a peça bruta ao longo da direção de corte para fora da cavidade da matriz, dada por
Fempurrando = n*kempurrando*F
c) A força de ejeção é a força necessária para levantar o blank contra a direção de corte para fora da cavidade da matriz, dada por
Fejetando = kejetando * F
onde:
- kdescarregamento - o coeficiente de força de remoção;
- kempurrando - o coeficiente de força de empurrão;
- kejetando - o coeficiente de força de ejeção;
- n - o número de peças na matriz, n = h/t (h é a altura da parede reta da borda da matriz, t é a espessura da peça de trabalho);
- F - a força de bloqueio (N).
Os coeficientes de força de descarga, força de empurrão e força de ejeção são fornecidos na Tabela 1.
Tabela 1: Proporções de força de descarga, força de alimentação, força de remoção e força de perfuração
| Espessura do material/mm | Kdescarregamento | Kperfuração | Kejetando | |
| Aço | ≤0.1 | 0.065 – 0.075 | 0.1 | 0.14 |
| >0. 1 ~0.5 | 0.045 – 0.055 | 0.063 | 0.08 | |
| >0.5 ~2.5 | 0.04 – 0.05 | 0.055 | 0.06 | |
| >2.5 ~6.5 | 0.03 – 0.04 | 0.045 | 0.05 | |
| >6.5 | 0.02 – 0.03 | 0.025 | 0.03 | |
| Alumínio e ligas de alumínio | 0.025 – 0.08 | 0. 03 ~ 0. 07 | ||
| Cobre puro e latão | 0.02 – 0.06 | 0.03 ~ 0.09 | ||
I. Cálculo da força de perfuração
A magnitude da força de punção P depende do comprimento total dos perímetros interno e externo da punção, da espessura do material e da resistência à tração, e está relacionada à taxa de resistência ao escoamento do material, que pode ser calculada pela seguinte fórmula
P = fLtRm
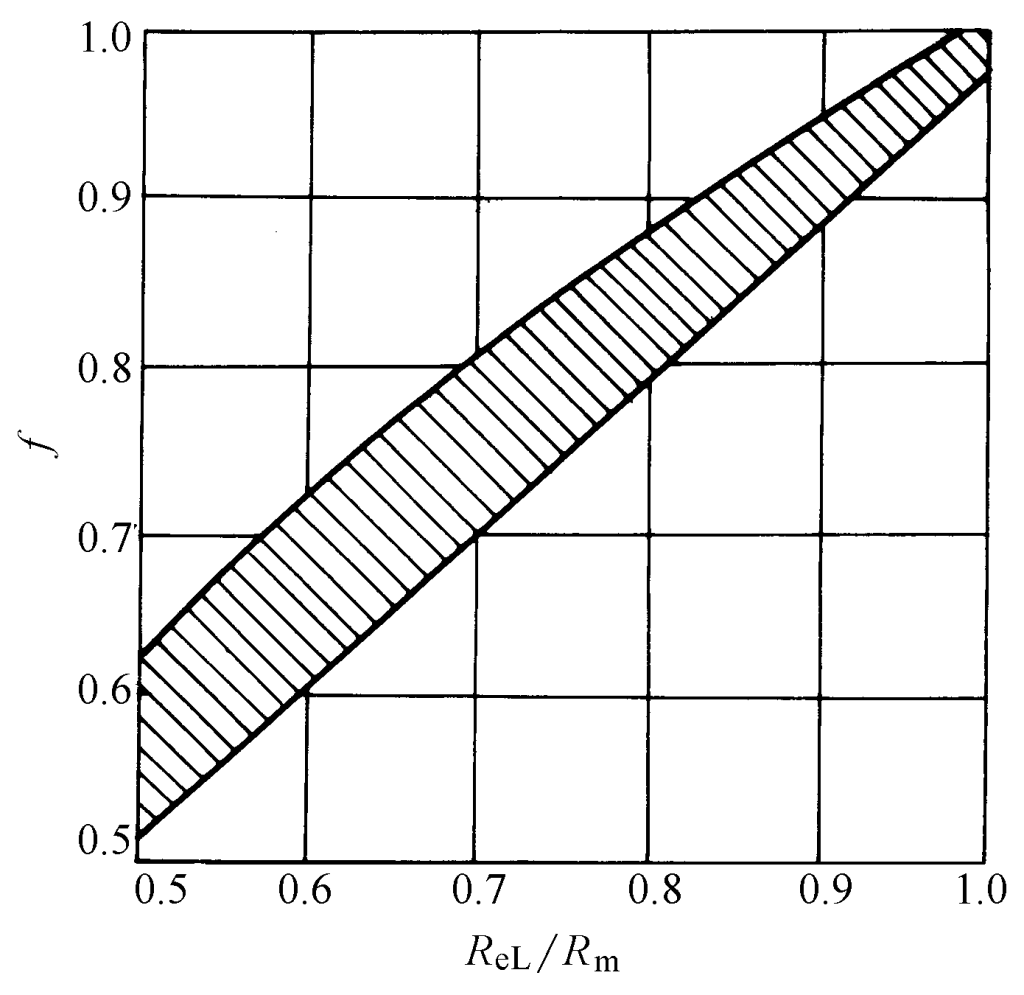
- O fator f, que depende da taxa de resistência do material, pode ser obtido na Figura 2-2-35, geralmente f é de 0,6 a 0,7;
- L - Comprimento total dos perímetros interno e externo da perfuração (mm);
- t-Espessura do material (mm);
- R m -Resistência à tração do material (MPa).
O método de cálculo acima foi proposto por Timmerbeil. f=1-t'/t, em que t' é a profundidade em que o punção pressiona o material quando ocorre a força máxima de punção (ou seja, a força de punção P na fórmula acima) e está relacionada à taxa de resistência ao escoamento do material.
A força de perfuração calculada usando a fórmula acima é bastante consistente com a realidade e foi incorporada aos padrões alemães. Além disso, as propriedades mecânicas fornecidas pelas matérias-primas incluem a resistência à tração do material R m e menor resistência ao escoamento R eL e sua proporção é usada para obter f da Figura 2-2-35, calculando assim a força de perfuração, que é conveniente para uso.
II. Força de descarga, força de empurrão e força de ejeção
Após a conclusão da operação de puncionamento, a peça de trabalho puncionada (ou sucata) sofre deformação elástica radial e se expande, enquanto o furo na sucata (ou peça de trabalho) sofre contração elástica radial. Ao mesmo tempo, a peça de trabalho e a sucata tentam recuperar sua curvatura elástica. O resultado dessas duas recuperações elásticas faz com que a peça de trabalho (ou sucata) fique presa na cavidade da matriz e a sucata (ou peça de trabalho) se prenda firmemente ao punção.
A força usada para descarregar a peça de trabalho (ou sucata) do punção é chamada de força de descarga. A força usada para empurrar a peça de trabalho (ou sucata) para fora da cavidade da matriz na direção do puncionamento é chamada de força de empurrar. A força usada para ejetar a peça de trabalho (ou sucata) da entrada da cavidade da matriz na direção oposta à da punção é chamada de força de ejeção (consulte a Figura 2-2-36). Obviamente, essas forças devem ser consideradas ao selecionar a tonelagem da prensa e ao projetar o molde.
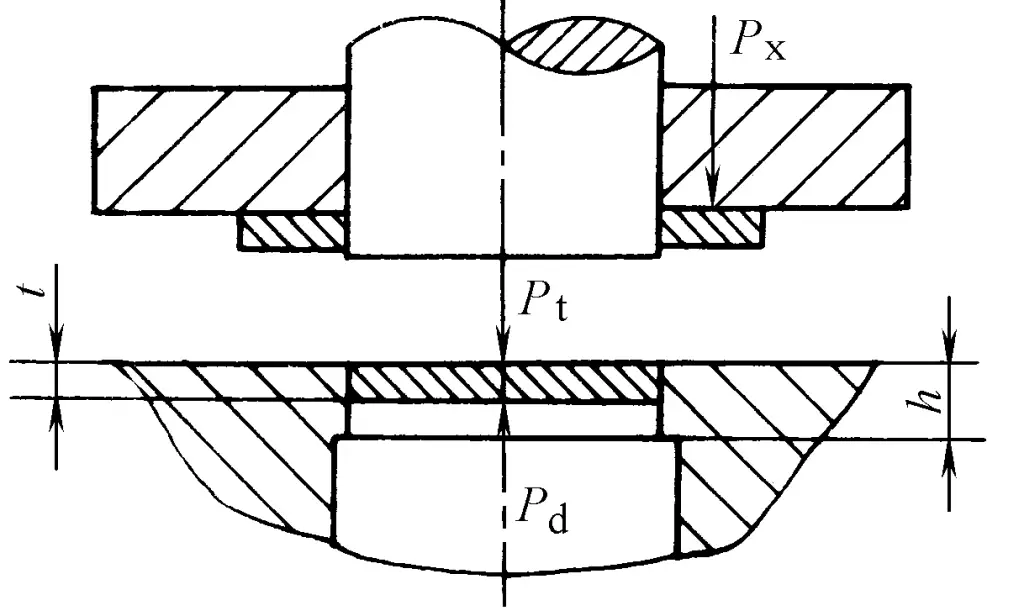
Muitos fatores afetam essas forças, incluindo principalmente: as propriedades mecânicas e a espessura do material, a forma e o tamanho da peça de trabalho, a folga entre os moldes, o tamanho da sobreposição do layout e as condições de lubrificação, etc. Devido à complexa influência desses fatores, é difícil calcular com precisão. Na produção, as seguintes fórmulas empíricas são comumente usadas para o cálculo
Px =KxP
Pt =nKtP
Pd=KdP
- P x , P t , P d - Força de descarga, força de empurrão e força de ejeção (N);
- K x , K t , K d - Os valores dos coeficientes de força de descarga, força de empurrão e força de ejeção podem ser encontrados na Tabela 2-2-9;
- P - Força de perfuração (N);
- n - Número de peças de trabalho presas simultaneamente na cavidade da matriz, n = h/t;
- h - Altura da abertura da parede reta da cavidade da matriz (mm);
- t - Espessura do material (mm).
Tabela 2-2-9 Valores dos coeficientes K x , K t , K d
| Material e espessura / mm | Kx | Kt | Kd | |
| Aço | ≤0.1 | 0.065~0.075 | 0.1 | 0.14 |
| >0.1~0.5 | 0.045~0.055 | 0.065 | 0.08 | |
| >0.5~2.5 | 0.04~0.05 | 0.055 | 0.06 | |
| >2.5~6.5 | 0.03~0.04 | 0.045 | 0.05 | |
| >6.5 | 0.02~0.03 | 0.025 | 0.03 | |
| Alumínio, liga de alumínio | 0.025~0.08 | 0.03~0.07 | ||
| Cobre puro, latão | 0.02~0.06 | 0.03~0.09 | ||
Observação: K x deve assumir o valor limite superior ao perfurar vários orifícios, flanges grandes e contornos complexos.
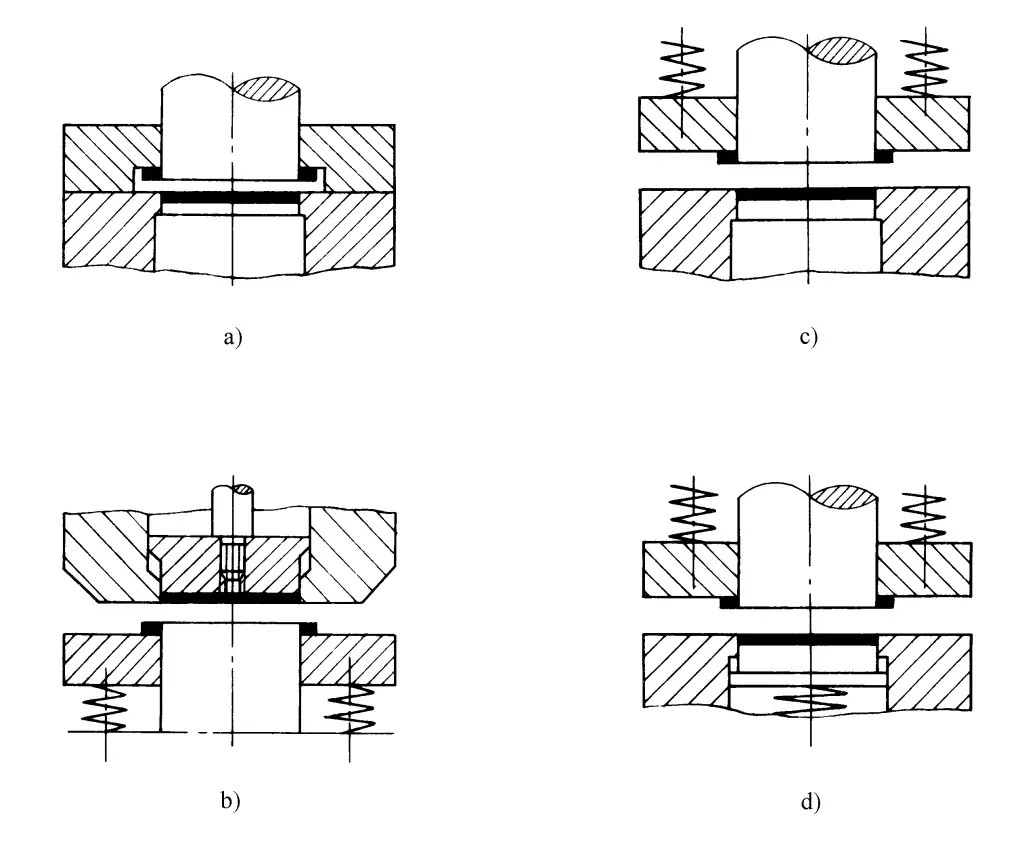
Ao selecionar a tonelagem da prensa, o fato de essas forças serem consideradas na força total de perfuração depende dos diferentes tipos de estrutura do molde (consulte a Figura 2-2-37).
1) A força total de perfuração usando uma placa de remoção rígida (consulte a Figura 2-2-37a) é
Pz=P+Pt
2) A força total de perfuração usando um ejetor rígido, molde invertido com removedor elástico (consulte a Figura 2-2-37b) é
P z = P + P x
3) A força total de perfuração usando uma placa de descarga elástica (consulte a Figura 2-2-37c) é
P z = P + P t + P x
4) A força total de perfuração usando peças superiores elásticas e descarga elástica (consulte a Figura 2-2-37d) é
P z = P + P d + P x
III. Força de fixação
Força de fixação P y é a força de restrição obrigatória na chapa metálica, um método eficaz para melhorar a qualidade da seção transversal da peça de trabalho e reduzir o abaulamento. A força de fixação na superfície da matriz é fornecida por uma placa de fixação móvel e elástica. A força de fixação na face da extremidade do punção é fornecida por uma placa móvel de contrapressão. A magnitude da força de fixação pode ser calculada aproximadamente pela fórmula a seguir:
P y = (0,10 a 0,20)P
- P y - Força de fixação (N);
- P - Força de perfuração (N).
O valor do coeficiente depende das propriedades do material, com valores mais altos para materiais duros ou materiais com alto coeficiente de endurecimento por trabalho, e valores mais baixos para materiais macios.
Comparação de P x , P d e P y , P y é o maior. Portanto, ao projetar moldes, se a fixação for necessária, basta projetar o dispositivo de fixação elástica de acordo com P y que, além de conseguir a fixação, também pode fornecer força de descarga e força da parte superior confiáveis e suficientes. Se a fixação não for necessária, projete o dispositivo de descarga e o dispositivo da parte superior correspondentes de acordo com P x e P d respectivamente.
IV. Força lateral
Força lateral P c Por um lado, causa desgaste nos lados convexo e côncavo do molde e, por outro lado, quando a linha de puncionamento não é fechada (como puncionamento de um lado ou puncionamento de lâmina lateral), torna o molde convexo suscetível à deformação de flexão indesejada sob força lateral e até mesmo à quebra. Nesses casos, é necessário projetar o suporte traseiro para fornecer uma força de reação lateral semelhante em magnitude e oposta em direção a P c mantendo o equilíbrio básico da força lateral no molde convexo. Em geral, a força lateral P c pode ser calculado aproximadamente pela seguinte fórmula
P c = (0,30 a 0,38)P
- P c - Força lateral (N);
- P - Força de perfuração (N).
V. Métodos para reduzir a força de perfuração
Ao perfurar materiais de alta resistência ou peças de trabalho grossas e de grande porte, se a força de perfuração necessária exceder a tonelagem das prensas existentes na oficina, devem ser tomadas medidas para reduzir a força de perfuração. Em geral, são usados os seguintes métodos:
1. Puncionamento aquecido
A resistência ao cisalhamento do material diminui significativamente quando aquecido, reduzindo, assim, a força de perfuração. A desvantagem desse método é que o material forma uma camada de óxido após o aquecimento, e as condições de trabalho são ruins devido ao aquecimento. Portanto, ele geralmente só é adequado para chapas grossas ou peças de trabalho em que a qualidade da superfície e a precisão dimensional não são muito exigidas.
A Tabela 2-2-10 lista a resistência ao cisalhamento do aço quando aquecido. Ao calcular a força de perfuração aquecida, τ b deve ser tomada com base na temperatura real de estampagem. Devido à dissipação de calor, a temperatura de estampagem é geralmente 150 a 200°C mais baixa do que a temperatura de aquecimento. Além disso, os efeitos da expansão e da contração térmica nas dimensões da peça de trabalho, bem como o amolecimento do material durante a punção a quente, devem ser considerados, e a folga do molde deve ser adequadamente menor do que durante a punção a frio.
Tabela 2-2-10 Resistência ao cisalhamento do aço quando aquecido
| Grau do material | τ na seguinte temperatura b / MPa | |||||
| 200°C | 500°C | 600°C | 700°C | 800°C | 900℃ | |
| Q195, Q215, 10, 15 | 360 | 320 | 200 | 110 | 60 | 30 |
| Q235, Q255, 20, 25 | 450 | 450 | 240 | 130 | 90 | 60 |
| Q275, 30, 35 | 530 | 520 | 330 | 160 | 90 | 70 |
| Q295, 40, 45, 50 | 600 | 580 | 380 | 190 | 90 | 70 |
2. Arranjo escalonado de punções
Na estampagem com vários punções, os punções são feitos em alturas diferentes em um arranjo em degraus, o que permite que os punções entrem em contato com o material em momentos diferentes, evitando a ocorrência simultânea de máximos força de bloqueio em cada punção, reduzindo assim a força de corte.
O cálculo da força de corte para punções organizados em etapas deve ser determinado pela soma das forças máximas de corte dos punções na mesma altura.
Os princípios a seguir devem ser considerados ao usar punções organizados em etapas:
1) A diferença na altura do punção h está relacionada à resistência à tração do material (consulte a Tabela 2-2-11).
Tabela 2-2-11 Relação entre a diferença de altura do punção h e a resistência à tração do material
| Resistência à tração do material R m /MPa | h/mm |
| <200 | 0.8t |
| 200~500 | 0.6t |
| >500 | 0.4t |
Observação: t é a espessura do material.
2) A distribuição de cada soco deve prestar atenção à simetria e à proximidade do centro de pressão.
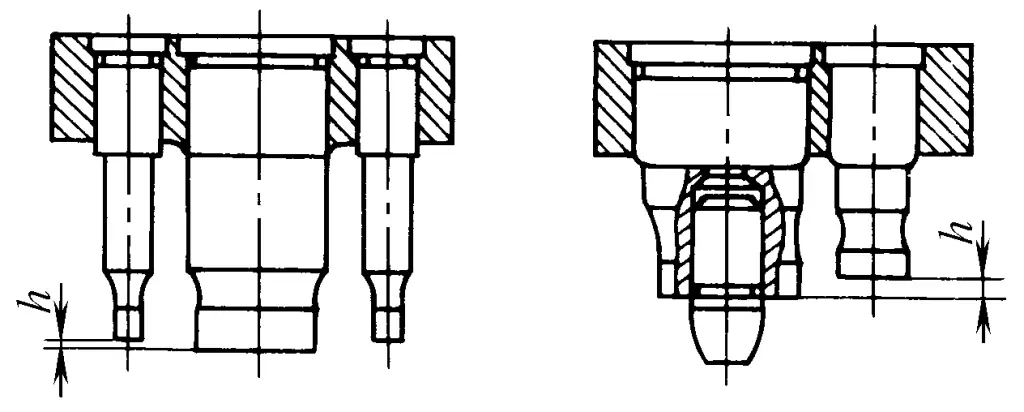
3) O primeiro punção a começar a trabalhar deve ser o que tem um pino-guia na extremidade (veja a Figura 2-2-38), ou fazer o punção maior mais longo e o menor mais curto, o que pode evitar que o punção menor se quebre ou se incline devido à pressão do fluxo de material. Além disso, tornar o punção menor mais curto melhora sua rigidez, evita a instabilidade longitudinal e aumenta sua vida útil.
3. Punção com matriz de borda chanfrada
Ao perfurar com uma matriz de borda plana, tosquia ocorre ao redor de todo o perímetro da peça de trabalho simultaneamente, de modo que a força de puncionamento costuma ser muito grande ao puncionar peças de trabalho grandes e espessas.
Ao usar uma matriz de borda chanfrada para perfuração, semelhante ao cisalhamento chanfrado, a borda inteira não entra em contato com o perímetro da peça de trabalho simultaneamente, mas perfura o material gradualmente, reduzindo significativamente a força de perfuração e a vibração e o ruído durante a perfuração.
Ao usar uma borda chanfrada para perfuração, para obter uma peça de trabalho plana, o punção deve ter uma borda plana e o chanfro deve estar na matriz, de modo que a peça de trabalho perfurada seja plana e a sucata seja dobrada (veja as Figuras 2-2-39a, b, c). Ao perfurar orifícios, a matriz deve ter uma borda plana e o chanfro deve estar no punção, de modo que os orifícios perfurados sejam planos e a sucata seja dobrada (veja as Figuras 2-2-39d, e, f). Ao projetar o chanfro, ele deve ser disposto simetricamente para evitar que a matriz (ou punção) sofra pressão lateral unilateral durante a perfuração, causando desalinhamento e danificando a borda.
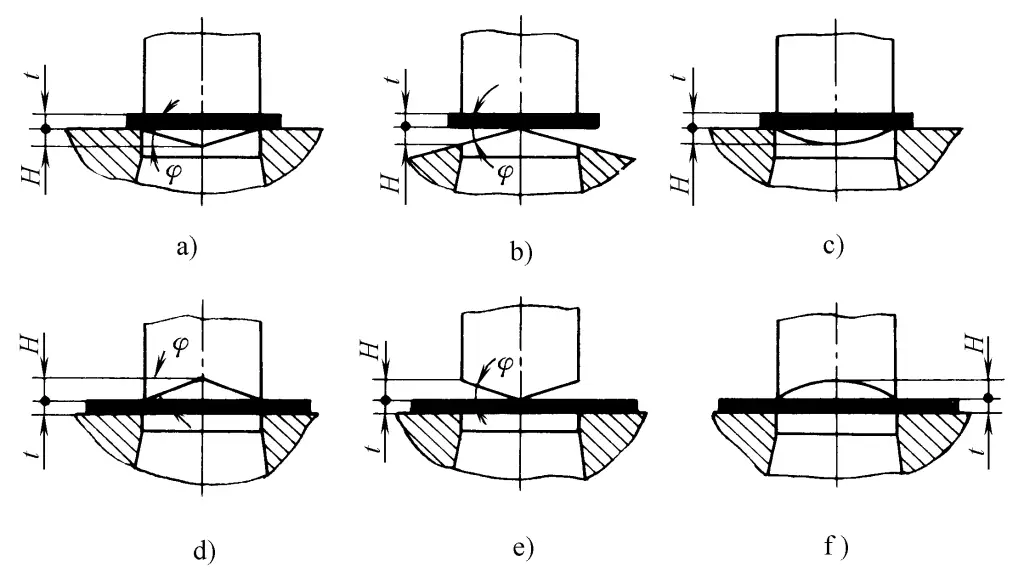
O grau de redução de força na perfuração do chanfro depende do ângulo do chanfro φ (consulte a Tabela 2-2-12).
Tabela 2-2-12 Parâmetros do bisel
| Espessura do material/mm | Altura da lâmina do bisel H/mm | Ângulo do chanfro φ/(°) | K |
| <3 | 2t | <5 | 0.3~0.4 |
| 3 ~10 | t | <8 | 0.6~0.65 |
A força de perfuração de cada lâmina chanfrada é calculada pela seguinte fórmula
Ps=KP
- P s - Força de perfuração da lâmina do bisel (N);
- K - Coeficiente de redução (consulte a Tabela 2-2-12);
- P - Força de perfuração da lâmina plana (N).
Para matrizes de perfuração grandes, ao fazer uma matriz de chanfro, o chanfro deve ser feito em uma forma ondulada simetricamente disposta (veja a Figura 2-2-40).
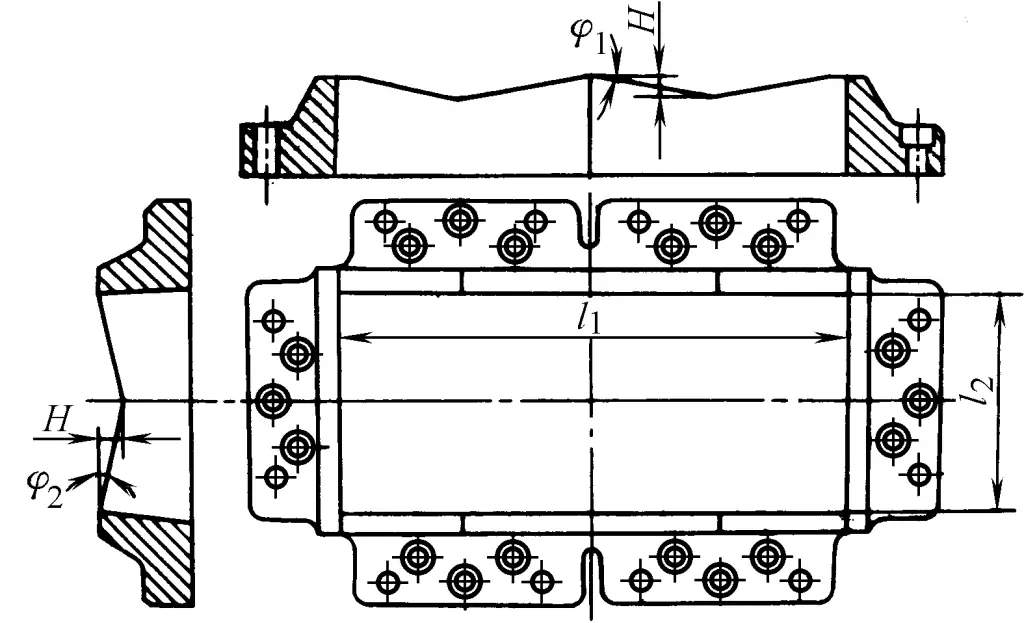
Embora a matriz chanfrada reduza a força de perfuração, ela aumenta a dificuldade de fabricação e retificação do molde, e a borda da lâmina também é propensa ao desgaste, portanto, geralmente é usada apenas para peças grandes e perfuração de chapas grossas.
VI. Poder de perfuração
1. Potência de perfuração da lâmina plana
A potência de perfuração de uma matriz de lâmina plana pode ser calculada pela seguinte fórmula
W =(xPt)/1000
- W - Potência de perfuração da lâmina plana (J);
- P - Força de perfuração (N);
- t - Espessura do material (mm);
- x - A razão entre a força de perfuração média e a força de perfuração máxima, x=P P /P é determinado pelo tipo e pela espessura do material; consulte a Tabela 2-2-13 para obter seu valor.
Tabela 2-2-13 Valores do coeficiente x
| Materiais | Espessura do material / mm | |||
| <1 | 1~2 | 2~4 | >4 | |
| Aço macio (τ b =250~350MPa) | 0.70~0.65 | 0.65~0.60 | 0.60~0.50 | 0.45~0.35 |
| Médio aço de dureza (τ b =350~500MPa) | 0.60~0.55 | 0.55~0.50 | 0.50~0.42 | 0.40~0.30 |
| Aço duro (τ b =500~700MPa) | 0.45~0.40 | 0.40~0.35 | 0.35~0.30 | 0.30~0.15 |
| Alumínio, cobre (recozido) | 0.75~0.70 | 0.70~0.65 | 0.65~0.55 | 0.50~0.40 |
2. Poder de perfuração da lâmina oblíqua
A potência de perfuração da matriz de lâmina oblíqua pode ser calculada pela seguinte fórmula
W s = x 1 P s (t+ H)/1000
Onde
- W s - Potência de perfuração da lâmina oblíqua (J):
- P s - Força de perfuração da lâmina oblíqua (N);
- H - Altura da lâmina oblíqua (mm);
- t - Espessura do material (mm);
- x 1 - Coeficiente, para aço macio, pode ser aproximado como: quando H=t, x 1 ≈0,5~0,6; quando H=2t, x 1 ≈0.7~0.8.
VII. Seleção do equipamento de estampagem
Quando o processo de estampagem envolve simultaneamente a força de corte, a força de alimentação e a força de ejeção, a força total de estampagem F é calculada da seguinte forma: Força total de estampagem Ftotal = F + Fdescarregamento + Fempurrando + Fejetando.
Nesse caso, a tonelagem da prensa selecionada deve ser aproximadamente 30% maior que Ftotal para fornecer a margem necessária.
Quando F, Fdescarregamento, Fempurrandoe Fejetando não ocorrem simultaneamente, Ftotal é calculado somando-se apenas as forças presentes no mesmo instante.
Na produção, os cálculos detalhados são normalmente realizados apenas para a força de perfuração, enquanto a força de descarga é estimada com base em uma proporção fixa da força de perfuração, mais a margem necessária para a perfuração, totalizando 50%.
Portanto, a fórmula para calcular a tonelagem da prensa é a seguinte:
Fimprensa = F × 150% = 1,5F