1. Изгибная пружина
Как и любая другая форма пластической деформации, изгиб трубы сопровождается упругой деформацией. Когда нагрузка снимается, волокна на внешней стороне нейтрального слоя укорачиваются из-за упругого восстановления, а волокна на внутренней стороне удлиняются, тем самым изменяя скорость изгиба и угол изгиба. Это явление известно как пружинящий откат. Существует две формы пружинящего отката, как показано на рисунке 4-25.
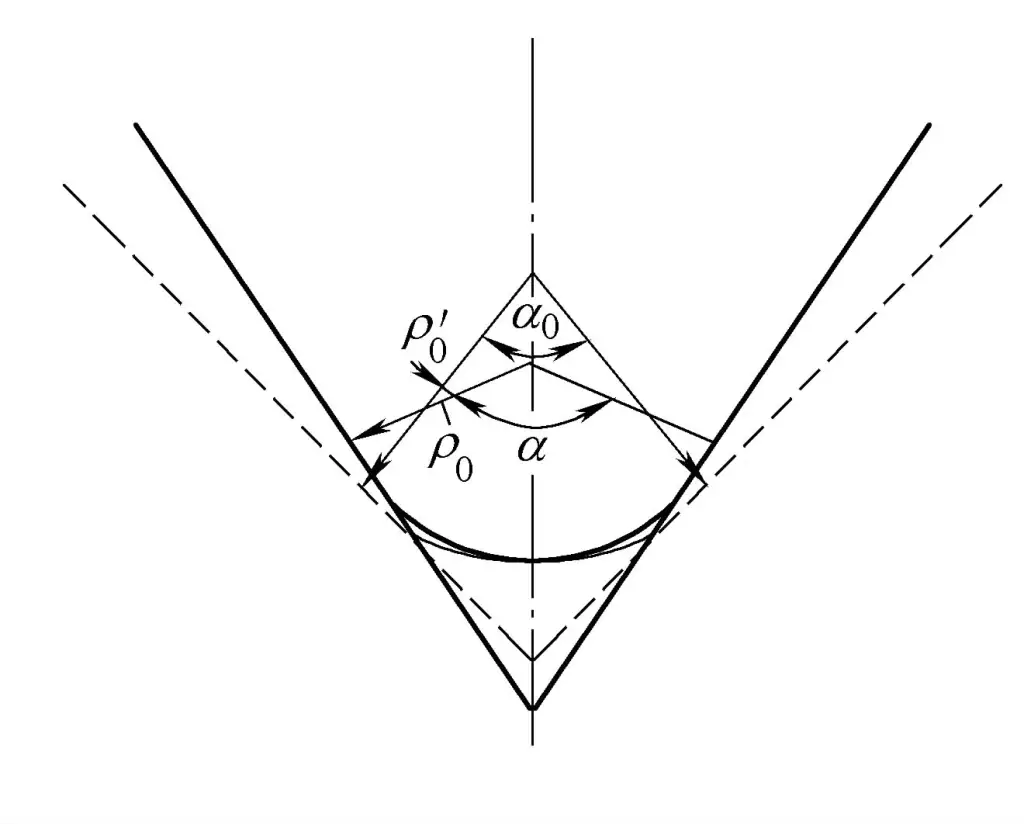
1) Кривизна уменьшается.
Кривизна уменьшается от 1/ρ0 перед разгрузкой до 1/ρ'0 после разгрузки.
2) Угол изгиба уменьшается.
Угол изгиба уменьшается от α перед разгрузкой до α 0 после разгрузки. Величина пружинящего отката может быть рассчитана по изменению кривизны ΔK или изменению угла изгиба Δα (также называемого углом пружинящего отката).
Δα = α - α 0
(1) Факторы, влияющие на пружинистость при изгибе
В процессе гибки существует множество факторов, влияющих на величину пружинящего отката, основными из которых являются следующие:
1) Механические свойства заготовки.
Чем меньше значение σs /E, то есть чем меньше σs и чем больше значение E, тем меньше величина упругости Δα.
2) Степень деформации r/t.
При одинаковых условиях, чем меньше r/t, тем больше степень деформации при изгибе, доля упругой деформации в общей деформации уменьшается, поэтому пружинистость при изгибе уменьшается.
3) Центральный угол изгиба α.
Чем больше центральный угол изгиба α, тем больше длина зоны деформации. При одинаковых условиях деформации количество деформаций на единицу длины уменьшается. Поэтому, чем больше угол изгиба α, тем больше доля упругой деформации в общей деформации, соответственно, увеличивается, и величина пружинящего отката Δa становится больше.
4) Зазор в матрице Z.
Крупнее зазор между штампамиУвеличенная пружинящая спинка.
5) Метод сгибания.
Величина пружинящего отката мала в процессе вытяжной гибки, и наименьшая - в процессе гибки давлением.
6) Форма заготовки и состояние структуры материала.
Сложные формы, многократное взаимное растяжение приводят к малой пружинящей посадке и большой пружинящей посадке после холодной закалки.
7) Структура пресс-формы и величина усилия прессования.
Усилие прижима кромки велико, что приводит к небольшому отскоку после сгибания заготовки.
(2) Определение величины отскока
Определение величины отскока заготовки позволяет принять соответствующие меры для преодоления отскока, чтобы согнутая заготовка отвечала требованиям точности, предъявляемым конструкторской схемой. Методы определения величины отскока включают в себя метод диаграмм, метод таблиц и метод расчета.
В действительности гибка формовкаС другой стороны, из-за наличия поперечных искажений и проблем со смятием, эти проблемы будут влиять на отскок; с другой стороны, трудно точно определить нейтральный слой в процессе гибки профилей, что делает расчет отскока более сложным. Расчет отскока при гибке профиля намного сложнее, чем при гибке листа, поэтому методы расчета отскока гибка труб все они являются приблизительными и сильно отличаются от реальной ситуации.
В настоящее время как в стране, так и за рубежом продолжаются исследования отскока. Поскольку отскок зависит от многих факторов и является довольно сложным процессом, в настоящее время не существует точной формулы расчета. Поэтому для контроля величины отскока обычно используются формы различной структуры, в основном корректируемые в процессе испытания форм.
(3) Методы уменьшения и предотвращения отскока
Методы уменьшения и предотвращения отскока можно разделить на две основные категории с точки зрения принципа действия. Первая категория методов обеспечивает сохранение формы детали после отскока за счет увеличения деформации. Основные меры этой категории заключаются в исправлении формы пресс-формы, уменьшении кривизны изгиба детали или увеличении угла изгиба, чтобы деталь после отскока соответствовала требованиям конструкции.
Другая категория методов заключается в уменьшении отскока путем изменения распределения напряжений в изогнутой деформированной детали. В этой категории наиболее часто используемой мерой является приложение касательного растягивающего напряжения, что делает распределение напряжений в поперечном сечении изогнутой детали равномерным, тем самым уменьшая неравномерность упругого восстановления при разгрузке и снижая величину отскока.
Отскок при гибочном формообразовании является одним из основных факторов, влияющих на точность размеров и эффективность производства деталей. Поскольку прогнозирование отскока тесно связано со всем процессом формообразования, проблема отскока является достаточно сложной и представляет собой актуальный и трудный момент в исследованиях гибка профиля формирование. Многие ученые в стране и за рубежом провели глубокие исследования и дискуссии.
В настоящее время существует несколько методов решения проблемы отскока при гибке труб:
1) Перечислите таблицу данных отскока, основываясь на опыте.
Например, несколько отечественных судостроительных заводов приобрели системы ЧПУ трубогибочные станки от американской компании WALLACE COAST, которые используют набор опытных данных в системе управления для компенсации отскока. Однако из-за большой погрешности этого метода точность гибки на трубогибочном станке с ЧПУ не является идеальной.
2) Используйте теоретические методы расчета.
Поскольку силовая ситуация при изгибе труб очень сложна, при расчетах необходимо делать допущения и упрощения, а свойства материалов и реальные условия работы трудно предсказать, до сих пор не было найдено успешных прецедентов использования теоретических формул расчета отскока на практике, и требуется дальнейшее обсуждение.
3) В авиа- и автомобилестроении уже много лет используется метод, представленный американской компанией EATON LEONARD.
Этот метод предполагает, что, несмотря на множество факторов, влияющих на отскок при гибке труб, после настройки станка параметры процесса (см.радиус изгиба, скорость гибки, сила зажима и т.д.) определяются, и в это время измеряется зависимость между углом гибки и углом формовки после отскока при условии гибки партии материальных труб, таким образом, угол поворота рычага трубогибочного станка и угол формовки трубы можно рассматривать как линейную зависимость.
Метод заключается в том, чтобы согнуть трубы на 125° и 22° на трубогибочном станке, а после того, как трубы согнуты, поместить их на станок для измерения формы труб с ЧПУ, чтобы измерить их фактические углы формирования 120° и 20°, установив уравнение прямой линии через две точки, можно получить соотношение между углом поворота рычага трубогибочного станка и требуемым углом формирования трубы. Этот метод дает хороший эффект.
Для решения проблемы отскока при гибке труб была проведена следующая работа:
1) Было проведено большое количество экспериментов по отскоку.
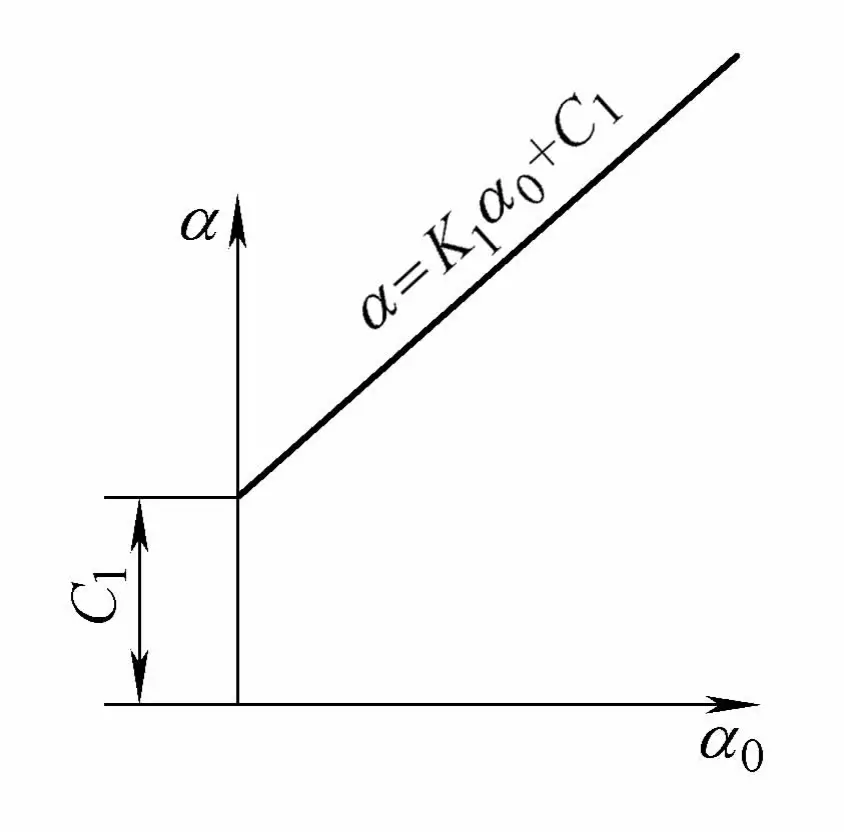
В результате проведения экспериментов по гибке труб без сердечника и с сердечником различных спецификаций на нескольких трубогибочных станках и выполнения расчетов регрессионного анализа измеренных данных стало известно, что угол изгиба α и угол формовки α 0 изменяется линейно, что согласуется с теоретическим расчетом линейного изменения. Однако, с другой стороны, эта линия не проходит через начало координат, существует отрезок расстояния C1 как показано на рисунке 4-26.
α = K1 α0 + C1
В формуле K1 это наклон прямой линии;
C1 это перехват прямой линии.
Из приведенной выше формулы можно сделать следующий вывод: Для труб, согнутых из одной и той же партии материала, в пределах диапазона инженерных углов гибки, зависимость между углом гибки α и углом формовки α 0 всегда является прямой линией, не проходящей через начало координат.
2) Теоретический анализ эксперимента по пружинящему изгибу трубы.
Для того чтобы проанализировать правильность выводов, сделанных по результатам эксперимента с пружинной откаткой, был проведен силовой анализ условий работы трубогибочного станка, и после принятия некоторых допущений и упрощений был выполнен большой объем расчетов.
Результаты расчетов показывают, что в меньшем диапазоне углов изгиба зависимость между углом изгиба α и углом формовки α 0 изогнута, и после того, как угол изгиба становится больше 1, соотношение между углом изгиба α и углом формирования α 0 является линейным и соответствует линейной зависимости, наблюдаемой в ходе эксперимента, что подтверждает правильность выводов эксперимента по пружинной нагрузке.
Следует отметить, что между этими двумя значениями существует значительная разница, которая обусловлена допущениями и упрощениями, сделанными в теоретических расчетах, а также тем, что реальные условия изгиба труб намного сложнее расчетных ситуаций.
Таким образом, вышеупомянутая работа идет глубже, чем результаты исследования, представленные компанией EATON LEONARD, которая рассматривает "зависимость между углом поворота рычага трубогибочного станка и углом изгиба трубы как линейную".
В целом, наилучшим методом решения проблемы пружинящего отгиба трубного материала в настоящее время является следующий: при гибке партии трубных материалов на данном трубогибочном станке можно провести эксперименты с двумя различными изгибами (например, 30° и 90°). Во время эксперимента записывайте два фактических угла поворота рычага трубогибочного станка α1 , α2 и измерьте два образующих угла трубы α01 , α02 . Затем рассчитайте коэффициенты по приведенной ниже формуле.
K1 = (α 2 - α 1 ) / (α 02 - α 01 )
C1 = α 1 - α 1 (α 2 - α 1 ) / (α 02 - α 01 )
Подставив две вышеприведенные формулы в формулу для α в эксперименте по отскоку, получим линейное уравнение, которое является правилом отскока для данной партии трубного материала.
2. Удлинение при изгибе
После сгибания на гибочном станке осевая длина трубы определенной длины увеличивается, это явление известно как удлинение при изгибе. Увеличение осевой длины называется удлинением трубы. Удлинение при изгибе влияет на точность размеров деталей. В прошлом для решения этой проблемы использовались следующие методы:
1) Для использования в производстве была составлена таблица данных по удлинению, основанная на опыте, но при использовании этого метода возникает большая погрешность.
2) Методы расчета, связанные с теорией удлинения при изгибе труб. Как и в случае с отбоем, в настоящее время не существует теоретической формулы расчета, которая успешно применялась бы на практике, что все еще требует дальнейшего обсуждения.
3) В авиационной и автомобильной промышленности уже много лет используется метод, представленный компанией EATON LEONARD, который заключается в том, что при измерении отвода трубным профилемером с ЧПУ по формуле рассчитывается так называемая константа дуги, которая представляет собой длину материала, используемую при угле изгиба 100°, а также учитывается, что удлинение трубы прямо пропорционально углу формовки.
Для решения проблемы удлинения при гибке труб была проведена следующая работа:
1) Было проведено большое количество экспериментов по удлинению.
Проведя эксперименты по гибке без сердечника и с сердечником на различных гибочных станках на пяти верфях и выполнив расчеты регрессионного анализа данных, полученных от каждой партии материалов, стало известно, что удлинение △L имеет линейную зависимость от угла формовки α', которая не проходит через начало координат. То есть:
ΔL = K 2 α'+C 2
В формуле,
- K 2 - наклон линии;
- C 2 - прямая линия.
В результате регрессионного анализа измеренных данных коэффициент корреляции γ составляет от 0,97 до 0,99, что свидетельствует о наличии четкой линейной зависимости. Таким образом, можно сделать следующий вывод: Для труб из одной и той же партии материалов в диапазоне инженерных углов изгиба удлинение ΔL и угол формовки α' имеют линейную зависимость, которая не проходит через начало координат.
2) Проверка регрессии также была проведена на таблицах данных по пружинящей посадке, полученных на соответствующих верфях.
Из эмпирических расчетов известно, что удлинение ΔL и угол формования α' также имеют линейную зависимость, причем коэффициент корреляции γ превышает 0,99, что указывает на высокую линейность, но интерцепт обычно мал.
3) Теоретический анализ эксперимента по удлинению трубы при изгибе.
Для дальнейшего подтверждения правильности выводов эксперимента по удлинению был проведен силовой анализ условий гибки труб на трубогибочном станке, и после принятия некоторых допущений и упрощений был выполнен большой объем расчетов. Результаты расчетов показывают, что в диапазоне малых углов изгиба удлинение ΔL и угол формовки α' имеют криволинейную зависимость; когда угол изгиба превышает 3°, удлинение ΔL и угол формовки α' имеют линейную зависимость.
Линейная зависимость в теоретическом анализе и тренд линейной зависимости в ходе эксперимента совпадают, что подтверждает правильность выводов эксперимента по удлинению трубы при изгибе. Следует отметить, что между этими двумя значениями существует значительная разница, которая обусловлена допущениями и упрощениями в теоретических расчетах, а также тем, что реальные условия изгиба труб гораздо сложнее расчетных.
Вывод исследования о том, что для труб из одной партии материалов в диапазоне инженерных углов гибки удлинение ΔL и угол формовки α' имеют линейную зависимость, не проходящую через начало координат, отличается от традиционно принятого мнения о том, что удлинение прямо пропорционально углу формовки, и в большей степени соответствует реальной ситуации при гибке труб трубогибочным станком.
В целом, наилучший подход к проблеме удлинения при изгибе трубных материалов на сегодняшний день следующий: при гибке партии трубных материалов на данном трубогибочном станке можно провести два эксперимента с одинаковой длиной L, но разными изгибами (например, 30° и 90°). После проведения эксперимента следует снять трубы и измерить два фактических угла формовки α' 1 , α' 2 и увеличенные длины двух фактических осей труб L' 1 , L' 2 , тогда можно рассчитать удлинение.
ΔL1 = (L1 '-L) ΔL2 = (L2 '-L)
Из этого следует, что коэффициенты линейного уравнения, связанного с ΔL, могут быть рассчитаны по следующим двум формулам.
K 2 = (ΔL 2 -ΔL 1 ) / (α' 2 -α' 1 )
C 2 = ΔL 1 -α' 1 (ΔL 2 -ΔL 1 ) / (α' 2 -α' 1 )
Подставив два вышеприведенных уравнения в линейное уравнение относительно ΔL, можно получить закон удлинения данной партии труб. Интеллектуальный измерительный прибор для гибки труб может удобно получить этот закон удлинения.
3. Метод решения проблемы радиуса формовки после гибки трубы и пружинящего отката
После того как материал трубы сгибается и пружинит, его радиус формовки R' становится больше радиуса формы R, что приводит к изменению точки касания трубы. Поэтому при гибке труб гибочный станок должен учитывать изменение начальной точки гиба, вызванное этим. Метод, используемый компанией EATON LEONARD, заключается в использовании трубного профилометра с ЧПУ для измерения соответствующих параметров пружинного отката, затем вычислении радиуса формовки после пружинного отката по формуле и использовании этого расчетного радиуса для коррекции начальной точки гиба.
При использовании этой формулы для определения начальной точки гиба выяснилось, что при гибке труб малой толщины (например, <3 мм) ошибка хотя и больше, но все же пригодна для использования; при гибке труб большей толщины ошибка особенно велика, и эффект не очень хороший. Это также связано с очень сложной ситуацией при гибке труб и трудностью прогнозирования свойств материала и реальных условий работы, что делает теоретическую формулу расчета радиуса формовки неспособной удовлетворить реальные потребности.
Если начальная точка гибки не обработана должным образом, трудно обеспечить точность гибочного формования, а при реализации процесса гибки без зазора возникнут трудности. Для решения этой проблемы необходимо использовать современные измерительные приборы.
На определенном трубогибочном станке измеряется радиус формовки партии трубных материалов после гибки и пружинения, что служит основой для определения начальной точки гибки в процессе. Интеллектуальный измерительный прибор для гибки труб может удобно получить радиус формовки трубного материала после гибки и пружинения, а принцип расчета измерений представлен в следующей формуле расчета.
4. Метод измерения упругости, удлинения и радиуса формовки с помощью интеллектуального измерительного прибора для гибки труб
Интеллектуальный измерительный прибор для гибки труб в основном основан на вышеупомянутом принципе гибки труб, специально разработан для использования с трубогибочными станками с ЧПУ. Прибор состоит из измерительного устройства (включая измерительный механизм, датчик угла) и микрокомпьютерной системы (включая микрокомпьютер, интерфейсную плату). Прибор обладает высокой точностью, угол составляет 0,1°, а длина - 0,25 мм.
Измерительный механизм прибора представляет собой четырехстержневой планарный механизм, как показано на Рис. 4-27, с датчиком угла, установленным в узлах a, b и c, который может измерять угол между двумя соседними стержнями. Измерительные головки в точках d и e являются плоскими, поэтому во время измерения стержни ad и be могут быть перпендикулярны прямому участку трубы dghe.
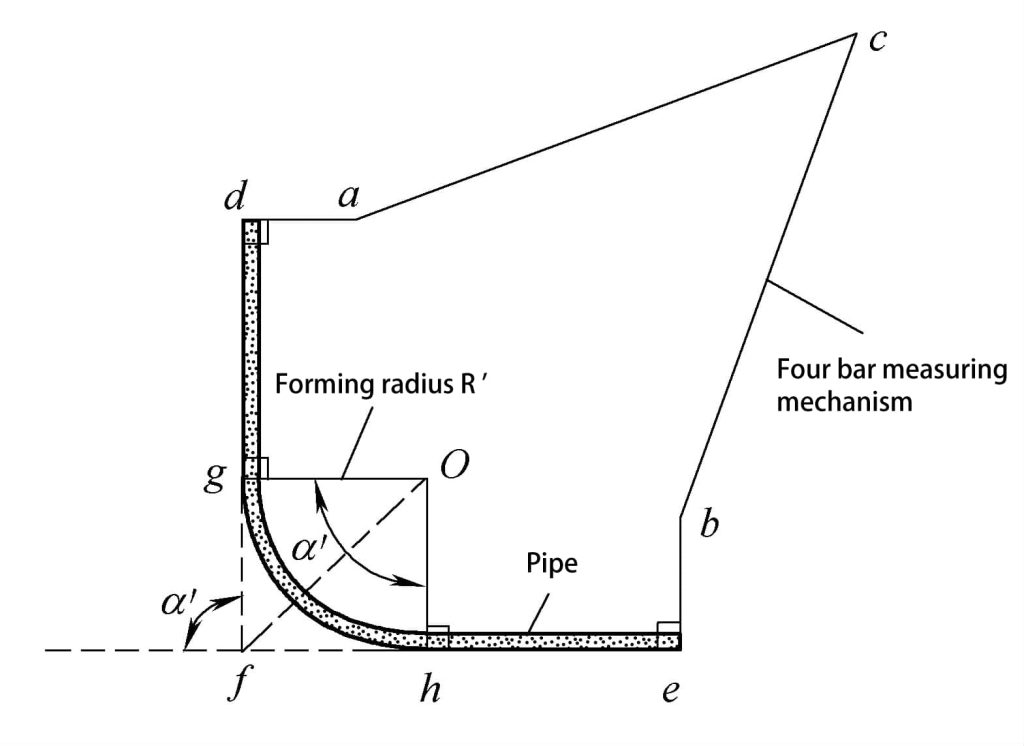
Длины каждого стержня в четырехбалочном плоском механизме известны, поэтому можно измерить и рассчитать соответствующие геометрические параметры трубы dghe. Метод заключается в следующем:
1) На основе известных условий работы механизма и угла, измеренного датчиком угла, можно рассчитать угол формирования α' трубы.
2) На основании известных условий работы механизма и угла, измеренного датчиком угла, можно рассчитать расстояния df и fe между точками пересечения оси прямой трубы.
3) Когда расстояние dg от начальной точки изгиба трубы фитинг известен, то фактический радиус формовки R' может быть рассчитан далее.
R'=O g = (df-dg) / tan(α'/2)
4) Далее можно рассчитать длину L' оси трубы.
L’=df+fe-2R’tan(α’/2) +πR’α’/180
Исходя из вышеприведенных принципов и формул, необходимо только согнуть на трубогибе два тестовых образца одинаковой длины L с начальными точками гиба на расстояниях d и g соответственно под заранее определенными углами (H 1 =30°, H=90°), затем удалите их и измерьте с помощью интеллектуального измерительного прибора для гибки труб, который может автоматически завершить фактическое измерение и распечатать шаблон изменения отскока, шаблон изменения удлинения и сформированный радиус после отскока различных металлических материалов и моделей труб.
Если задана форма трубы заготовки, прибор также может предоставить данные заготовки для гибки без припусков, а также программу обработки для трубогиба с ЧПУ, включая коррекцию начальной точки и компенсацию отскока (прибор также имеет функцию измерения формы трубы). Данные, предоставляемые прибором, не только значительно повышают точность формовки трубогиба с ЧПУ, но и способствуют технологическому прогрессу, достигая цели снижения трудоемкости, экономии стали и повышения эффективности производства.
5. Радиус изгиба
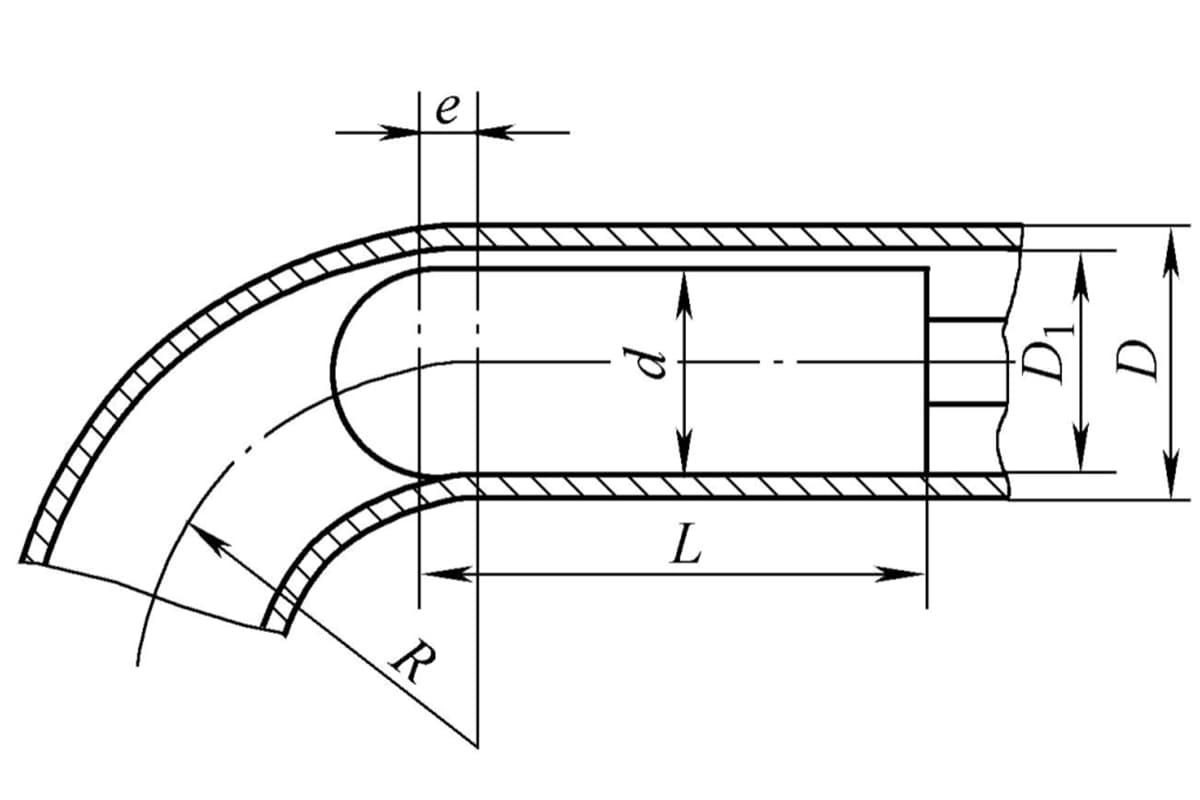
Степень деформации материала трубы при изгибе зависит от значений относительного радиуса изгиба R/D и относительной толщины t/D (R - радиус кривизны центрального слоя поперечного сечения материала трубы, D - внешний диаметр материала трубы, t - толщина стенки материала трубы). Чем меньше значения R/D и t/D, тем больше степень деформации при изгибе, внешняя стенка нейтрального слоя при изгибе станет чрезмерно тонкой, что может привести к разрыву; внутренняя стенка утолстится, даже станет неустойчивой и сморщится.
В то же время, при увеличении степени деформации искажение поперечного сечения (сплющивание) также будет более сильным. Поэтому для обеспечения качества формовки трубного материала необходимо контролировать степень деформации в допустимых пределах. Допустимая степень деформации при изгибе трубного материала называется пределом формования при изгибе. Предел формообразования при изгибе трубного материала зависит не только от механических свойств материала и метода гибки, но и от требований к использованию трубопроводной арматуры.
Для гнутых деталей общего назначения условием определения предела формообразования является максимальная деформация удлинения ε max образующаяся в наиболее удаленном от нейтрального слоя месте на внешнем участке области деформации изгиба, не должна превышать предельного значения, допускаемого пластичностью материала.
При условии, что внешний поверхностный слой вне зоны деформации при изгибе трубопроводной арматуры не растрескивается, предельный радиус изгиба r мин которая может быть согнута во внутреннюю сторону детали, используется как предел формовки при гибке трубного фитинга. r мин зависит от механических свойств материала, размера конструкции трубопроводной арматуры, метода обработки гибом и других факторов.
Минимальный радиус изгиба для различных методов обработки показан в таблице 4-6.
Таблица 4-6 Минимальный радиус изгиба для гибки труб (единицы измерения: мм)
| Методы гибки | Минимальный радиус изгиба (rмин) |
| Пресс для гибки | (3~5)D |
| Сгибание обмотки | (2~2.5)D |
| Гибка рулонов | 6D |
| Сгибание под давлением | (2.5~3)D |
Примечание: D - внешний диаметр трубы.
Минимальный радиус изгиба для стальных и алюминиевых труб приведен в таблице 4-7.
Таблица 4-7 Минимальный радиус изгиба для стальных и алюминиевых труб (единицы измерения: мм)
| Наружный диаметр трубы | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| Минимальный радиус изгиба rмин | 8 | 12 | 16 | 20 | 28 | 32 | 40 | 45 | 50 | 56 |
| Наружный диаметр трубы | 24 | 28 | 30 | 32 | 35 | 38 | 40 | 44 | 48 | 50 |
| Минимальный радиус изгиба rмин | 68 | 84 | 90 | 96 | 105 | 114 | 120 | 132 | 144 | 150 |