Sac metal bükme parçaları için işlenmemiş parça boyutunun hesaplanması, bükme işlemi planının formüle edilmesi için bir ön koşuldur. Farklı teknisyenler proses dokümanlarında farklı bükme payı faktörleri seçebilir ve boşluk boyutunun doğruluğu, bükme parçalarının boyutsal doğruluğunu ve ürün kalitesini doğrudan etkiler.
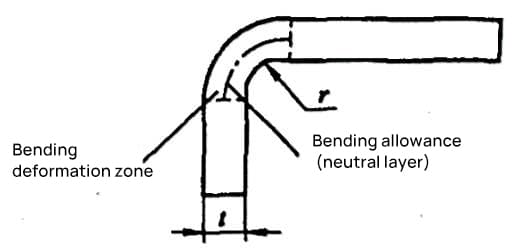
Bazen yanlış hesaplamalar atık ürünlere bile neden olabilir. Tipik bir basit bükme parçasının (bkz. Şekil 5-1) katlanmamış uzunluğu L = a + b - y'dir (burada y, R parçası için düzeltme değeri olarak da bilinen bükme kesintisidir).
Ancak, çeşitli kılavuzlarda ve materyallerde, φ=90° için eğilme kesintisi doğrudan elde edilebilirken, Şekil 5-2'de gösterildiği gibi 90° olmayan eğilmeler için teknisyenlerin bunu bir deneyim faktörüne (K faktörü) dayalı olarak hesaplamaları gerekir.
İlgili okuma: Sac Metal Açma Sanatı Açıklandı
1. Sac Metal Bükümlerinin Katlanmamış Boyutunu Hesaplama Prensibi
Bükülmüş bir işlenmemiş parçanın katlanmamış boyutu, nötr tabakanın uzunluğunun bükülmeden önce ve sonra değişmeden kalması ilkesine göre belirlenir. Sac büküldüğünde, boş bölümün dış katman lifleri gerilir ve iç katman lifleri sıkıştırılır.
Dış tabaka liflerinin gerilmesi dıştan içe doğru kademeli olarak azalır ve iç tabaka liflerinin sıkışması da içten dışa doğru kademeli olarak azalır.
Lifler gerilmeden sıkıştırmaya veya sıkıştırmadan gerilmeye geçtiğinde, gerilme ve gerinimin sıfır olduğu ve uzunluğunun bükülmeden önce ve sonra değişmeden kaldığı bir lif tabakası olmalıdır.
Bu katman, nötr katman olarak tanımladığımız katmandır. Bu nedenle, bükülmüş işlenmemiş parçanın katlanmamış boyutunu hesaplamanın anahtarı nötr tabakanın konumunu belirlemektir. Nötr tabakanın konumu, bükülmüş parçanın ve işlenmemiş parçanın hacminin plastik deformasyondan önce ve sonra eşit olması koşuluna göre belirlenir.
2. Nötr Katmanın Eğrilik Yarıçapının ρ Belirlenmesi
Teorik olarak, bükülen parçanın kalınlık yönü boyunca düzensiz deformasyon nedeniyle, nötr tabaka parabolik bir yüzeydir, ancak hesaplama uğruna genellikle dairesel bir yay yüzeyi olarak kabul edilir. Eğilme deformasyonu çok küçük olduğunda (r/t >6,5), nötr tabaka yaklaşık olarak malzeme kalınlığının ortasında kabul edilebilir, yani nötr tabakanın eğrilik yarıçapı ρ=r+t/2.
Deformasyon çok büyük olduğunda (r/t≤6.5), malzeme kalınlığı incelir ve Şekil 5-3'te gösterildiği gibi kesit distorsiyonu çok büyük olur.
Bu sırada, kesitteki tüm etkili kuvvetlerin sonuç kuvvetinin sıfır olduğu denge koşulunu sağlamak için, nötr tabaka malzemenin iç yüzeyine doğru hareket etmelidir.
Bu noktada, plastik deformasyon sırasında hacmin değişmemesi koşuluna, yani bükülmeden önceki hacme dayanarak nötr tabakanın eğrilik yarıçapını belirleyebiliriz: V0=LBt ve bükme sonrası hacim:
V=(R2-r2)α*B'/2.
Formülde, B işlenmemiş parçanın genişliği (mm); B' işlenmemiş parçanın büküldükten sonraki ortalama genişliği (mm); α ise bükme merkez açısıdır. Bükme öncesi ve sonrası hacmin eşit olması prensibine göre, V0=V, yani,
LBt=(R2-r2)α*B'/2 ve L=(R2-r2)α*B'/2tB (5-1).
Nötr tabakanın sıfır gerilme ve geriniminden L=l=αρ elde edilir; burada L nötr tabakanın deformasyonundan önceki uzunluk (mm) ve l nötr tabakanın deformasyonundan sonraki uzunluktur (mm).
Denklem (5-1)'i yerine koyarak şunları elde ederiz ρ=(R2-r2)B'/2tB. Yukarıdaki denklemde R=r+t' yerine koyarsak, denklemin başka bir şeklini elde edebiliriz ρ=(r/t+η/2)tβη (5-2)Burada β genişlik faktörüdür, β=B'/B, ve genellikle geniş bir plaka (B>3t) büküldüğünde, genellikle β=1 olarak kabul edilir; η incelme faktörüdür, η=t'/t.
Denklem (5-2) nötr tabakanın konumunu teorik olarak hesaplamak için kullanılan formüldür. Hesaplama yaparken η değerini, yani incelme kuralını bilmemiz gerekir. η değeri için Tablo 5-1'e bakılabilir.
İnceltme kuralının oldukça karmaşık olduğu, nötr tabakanın bükme alanındaki konumunun dağılımının tek tip olmadığı ve inceltme kuralının bükme yöntemi, bükme alt kalıp yuvasının genişliği ve malzeme kalınlığı gibi birçok faktörle de ilgili olduğu belirtilmelidir.
Bu durum, nötr tabakanın konumunun teorik hesaplamasına kaçınılmaz hatalar getirmekte ve böylece teorik belirleme yönteminin pratik uygulama değerini azaltmaktadır.
Tablo 5-1: İnceltme faktörü η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
Gerçek üretimde, nötr eksenin konumunu belirlemek için genellikle teorik hesaplamadan daha basit olan ampirik bir formül kullanılır, aşağıdaki gibi:
ρ = r + Kt (5-3)
Nerede?
- ρ - Tarafsız eksenin eğrilik yarıçapı (mm)
- r - Hammaddenin iç bükülme yarıçapı (mm)
- t - Malzeme kalınlığı (mm)
- K - Nötr eksen katsayısı (ampirik K faktörü), Tablo 5-2'ye bakın
Tablo 5-2: Tarafsız eksen katsayısı K'nin ampirik değerleri
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
Not:
- K1 üst plakalı veya baskı plakalı V şekilli veya U şekilli bükümler için geçerlidir.
- K2 üst plakası olmayan V şekilli dirsekler için uygundur.
3. Çeşitli Tipik Sac Metal Bükümleri için Boş Katlanmamış Boyutların Hesaplanması
Nötr katmanın tanımına göre, boş katlanmamış boyut nötr katmanın uzunluğuna eşit olmalıdır. Tipik olarak, iç kısma göre bükülme yarıçapı İşlenmemiş parçanın r değerine göre dirsekler yuvarlak köşeli ve yuvarlak köşeli olmayan dirsekler olarak kategorize edilir: r>0,5t olduğunda dirsekler yuvarlak köşeli, r<0,5t olduğunda yuvarlak köşeli olmayan olarak kabul edilir.
Ayrıca, B plaka genişliğine bağlı olarak, bükümler geniş ve dar plaka bükümleri olarak kategorize edilir: B>3t plaka genişliği olduğunda, geniş plaka bükümü olarak adlandırılır ve B<3t plaka genişliği olduğunda, dar plaka bükümü olarak adlandırılır.
Üretim pratiğinde, yuvarlak köşe yarıçaplı (r>0.5t) ve geniş plakalı (B>3t) bükümler en yaygın kullanılanlardır ve bükümlerin evrenselliği göz önüne alındığında, esas olarak büküm sırasında yuvarlak köşe yarıçaplı ve geniş plakalı bükümler için boş katlanmamış boyutların hesaplanmasını tartışıyoruz.
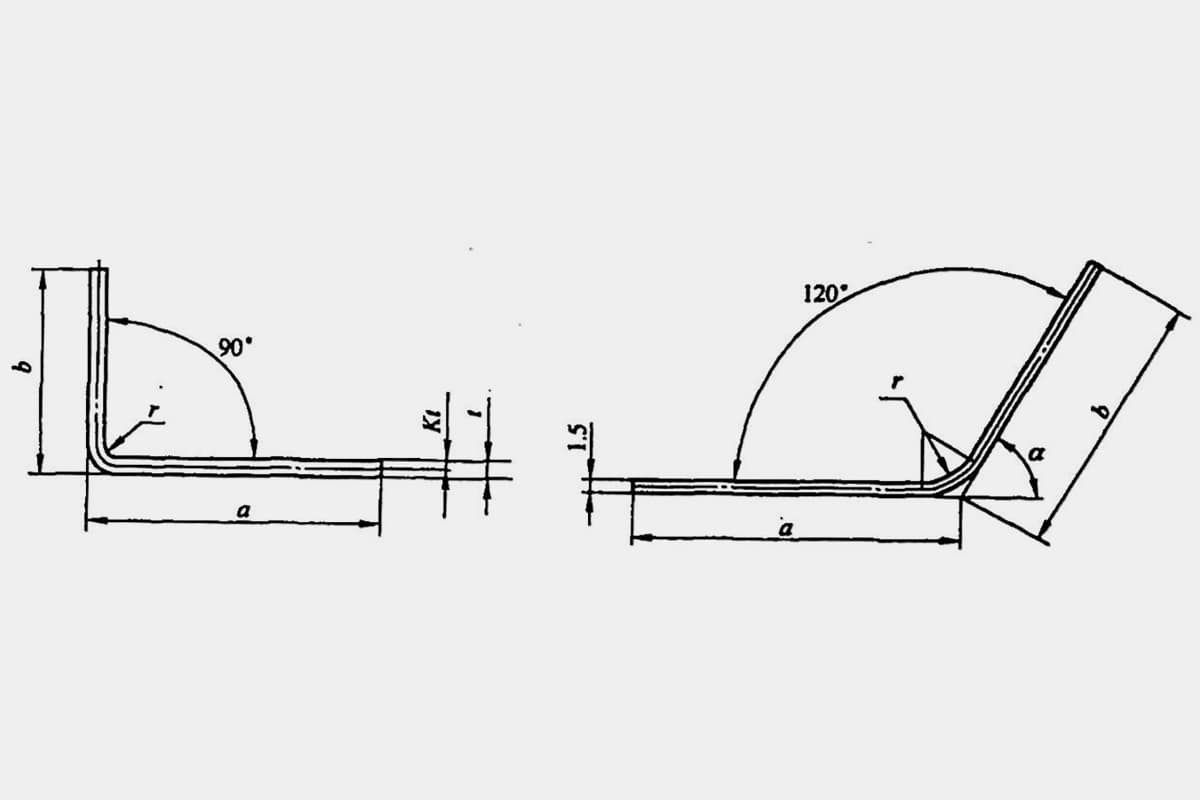
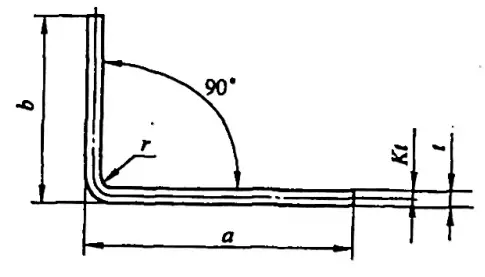
3.1 Yuvarlak Köşeli Dirsekler için Boş Katlanmamış Boyutların Hesaplanması (r>0,5t)
r>0,5t, B>3t olduğunda, bükme parçasının incelmesi şiddetli olmadığından ve kesitsel bozulma küçük olduğundan, boşluğun uzunluğu, nötr tabakanın uzunluğunun boşluğun katlanmamış boyutuna eşit olduğu ilkesine dayanarak belirlenebilir.
Yuvarlak köşeli dirseklerin (r>0.5t) boş katlanmamış boyutlarını hesaplamak için yaygın yöntemler, bükülme katsayısının hesaplanması ve bükülme kesinti değerinin hesaplanması olarak ikiye ayrılır.
1. Yuvarlak Köşeli Bükümler (r>0,5t) Boş Katlanmamış Boyutlar için Bükme Katsayısı Hesaplaması:
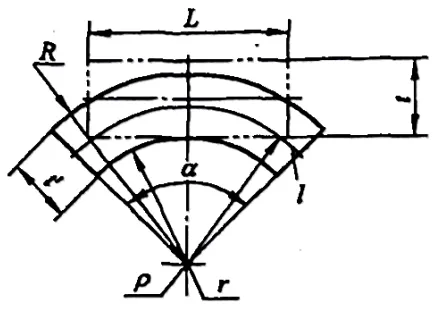
1) Eğilme katsayısı, Şekil 5-4'te gösterildiği gibi, eğilme deformasyon bölgesinin nötr tabakası (eğilme R kısmı) boyunca ölçülen yay kısmının uzunluğudur.
Eğilme katsayısı (5-4) formülü ile hesaplanır: x=παρ/180° (5-4)
Burada ρ nötr tabakanın eğrilik yarıçapıdır (mm).
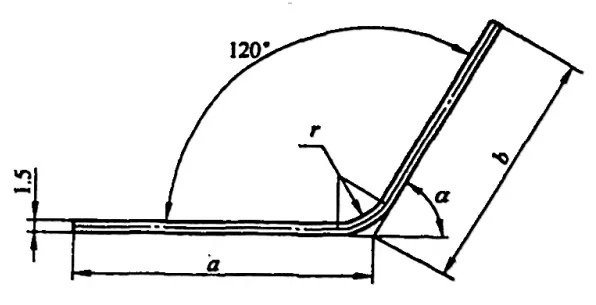
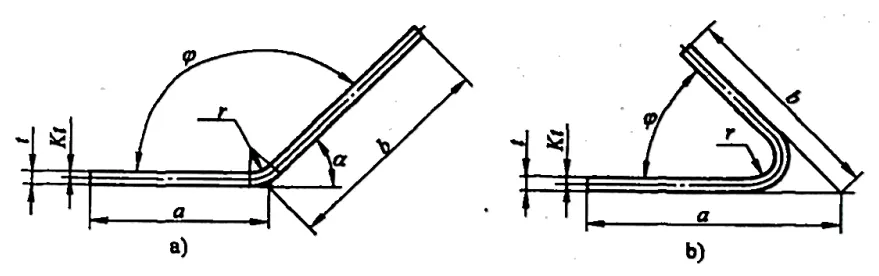
2) Şekil 5-5, boş katlanmamış boyutların bükülme katsayısı hesaplaması için boyut gösteriminin bir örneğini göstermektedir ve boş katlanmamış boyutların bükülme katsayısını hesaplamak için formülü aşağıdaki gibidir.

a) φ > 90° b) φ≤90
L=a+b+x (5-5)
Denklem (5-3)'ü denklem (5-4)'te yerine koyarak eğilme katsayısı formülünü elde ederiz:
x=πα(r+Kt)/180° (5-6)
Denklem (5-6)'yı denklem (5-5)'te yerine koyarak, bükülmüş boşluğun katlanmamış boyutunu hesaplamak için formülü elde ederiz:
L=a+b+πα(r+Kt)/180° (5-7)
Nerede?
- L - Boşluğun katlanmamış boyutu (mm);
- K - K-faktörü katsayısı, değeri için Tablo 5-2'ye bakın;
- α - Merkezi bükülme açısı, bükülen parçanın açısı ile ilişkisi α=180°-φ'dir;
- r - İşlenmemiş parçanın iç katmanının bükülme yarıçapı (mm);
- t - Malzemenin kalınlığı (mm);
- a, b - Sırasıyla bileşenin düz parçalarının uzunlukları (mm).
2. Yuvarlak köşeli bükülmüş bir parçanın katlanmamış boyutu için bükme kesintisinin hesaplanması (r>0.5t)
1) Bükme kesintisi (R kısmı için düzeltme değeri olarak da bilinir), Şekil 5-6'da gösterildiği gibi, bükme deformasyon bölgesinin (bükmenin R kısmı) R'sinin iki katı ile bükme katsayısı arasındaki farktır.

Eğilme kesintisi (R kısmı için düzeltme değeri) denklem (5-8) uyarınca hesaplanır:
y = 2R-παr/180° (5-8)
2) Şekil 5-7, boşluğun katlanmamış boyutu için eğilme kesintisinin hesaplanmasına yönelik bir boyut açıklama örneğini göstermektedir. Eğilme kesintisi y aşağıdaki formülle hesaplanır:
a)90°<φ≤165° b)φ≤90°
① φ ≤ 90° olduğunda:
R=(r+t)/tan(φ/2)
Yukarıdaki formülü ve formül (5-3)'ü formül (5-8)'de yerine koyarak, φ≤90°'lik bir bükülme için bükülme kesintisini (yani, R kısmının düzeltme değerini) elde ederiz (bkz. Şekil 5-7b):
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
②90°<φ≤165° olduğunda:
R=(r+t)tan[(180°-φ)/2]
Yukarıdaki formülü ve formül (5-3)'ü formül (5-8)'de yerine koyarak, 90°<φ≤165°'lik bir bükülme için bükülme kesintisini (yani R kısmının düzeltme değerini) elde ederiz (bkz. Şekil 5-7a):
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
③ 165°<φ≤180° olduğunda:
y≈0
3) Şekil 5-7'de gösterilen parçanın boş boyutunun eğilme kesintisi değerini hesaplamak için formül şöyledir:
L=a+b-y (5-11)
① φ≤90° olduğunda, formül (5-9)'u formül (5-11)'de yerine koyarak, boş boyutun bükülme kesinti değerini hesaplamak için aşağıdaki formülü elde ederiz:
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
② 90°<φ≤165° olduğunda, formül (5-10)'u formül (5-11)'de yerine koyarak, boş boyutun eğilme kesinti değerini hesaplamak için aşağıdaki formülü elde ederiz:
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
③ 165°<φ≤180° olduğunda:
L≈a+b (5-14)
Nerede?
- y - Bükme kesintisi (mm)
- L - Parçanın boş boyutu (mm)
- r - İşlenmemiş parçanın iç bükülme yarıçapı (mm)
- t - Malzeme kalınlığı (mm)
- α - Bükme merkezi açısı, bükme açısı ile ilişkisi α=180°-φ
- a, b-Bükme tepe noktasına kadar parçanın kenar uzunlukları (mm).
3. Çok açılı bükümler için boşluk boyutunun hesaplanması
Çok açılı bükümler için işlenmemiş parça boyutu, R kısmı ve düz kenarların uzunluklarının toplamıdır.
1) Bükme katsayısı ile çok açılı bükme boş boyutu hesaplaması:
L=l1+l2+...+ln+1+nx (5-15)
Nerede l1, l2...ln+1 parçanın her bir kenarının düz kısımlarının uzunluklarıdır (mm);
n, R dirseklerinin sayısıdır.
2) Bükme kesintisi ile çok açılı bükme boş boyutu hesaplaması:
L=l1+l2+...+ln+1-ny (5-16)
Nerede l1, l2...ln+1 parçanın kenarlarının bükülme tepe noktasına olan uzunluklarıdır (mm);
n, R dirseklerinin sayısıdır.
Örnek 5-1: Şekil 5-8'de gösterilen büküm için boşluk boyutunu hesaplayın.
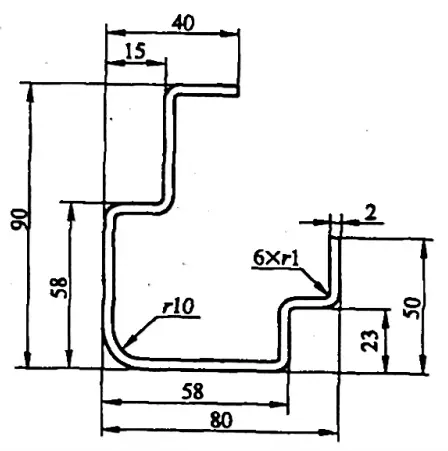
Çözüm 1: Eğilme katsayısını kullanarak boşluk boyutunu hesaplayın.
Ek A'ya bakınız: Bükme parçası açısı φ=90°, kalınlık t=2mm ve yarıçap r=10mm olduğunda, bükme katsayısı 2,68mm'dir;
Bükme parçası açısı 90°, kalınlık t=2mm ve yarıçap r=10mm olduğunda, bükme katsayısı x2=16.9mm'dir.
Denklem (5-5) ve (5-15)'ten bükülmüş parça için işlenmemiş parçanın düz boyutu şu şekilde hesaplanır:
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2,68 + 16,9]mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240,98 mm.
Çözüm 2: Bükme kesintisi değerini kullanarak işlenmemiş parçanın düz boyutunu hesaplayın.
Ek C'ye bakınız: φ=90° açılı, t=2mm kalınlıklı ve r=1mm yarıçaplı bir büküm için, R bölümü için düzeltme değeri y1=3,32mm'dir; φ=90° açılı, t=2mm kalınlıklı ve r=10mm yarıçaplı bir büküm için, R bölümü için düzeltme değeri y2=7,1mm'dir.
Bükülmüş parçanın ham boyutu denklem (5-11) ve (5-16)'dan elde edilebilir:
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3.32 - 7.1] mm
= (25+34+17+116+25+24+27-19.92-7.1) mm
= 240,98 mm
Örnek 5-2: Şekil 5-9'da gösterilen bükülmüş parçanın ham boyutunu hesaplayın.
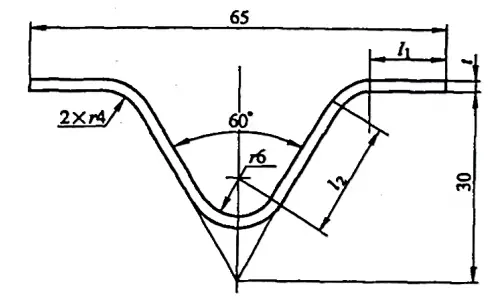
Çözüm: Bükülme katsayısını kullanarak ham boyutu hesaplayın.
Denklem (5-5) ve (5-15)'ten bükülmüş parçanın boş boyutlarını hesaplamak için formül şöyledir:
L=2l1+2l2+2x1+x2
nerede l1 = [32,5 - (30tan30°+4tan30°)] mm = 12,87 mm
ve ben2 = [(30/cos30°) - (8/tan30°+4tan30°)] mm = 18,47 mm
Ek A'ya başvurulduğunda: φ=120° bükülme açısı, t=2mm, r=4mm olduğunda, bükülme faktörü değeri x1=4.98mm; bükülme açısı φ=60°, t=2mm, r=6mm olduğunda, bükülme faktörü değeri x2=14,16 mm.
Bu değerler formülde yerine konduğunda, boş katlanmamış uzunluk L= (2×12.87 + 2×18.47 + 2×4.98 + 14.16) mm = 86.8 mm olarak elde edilir.
Daha düşük hassasiyet gereksinimleri olan daha basit bükümler için işlenmemiş parçanın katlanmamış boyutlarının doğrudan hesaplanabileceği unutulmamalıdır. Bununla birlikte, daha karmaşık bükümler veya daha yüksek hassasiyet gereksinimleri olanlar için, işlenmemiş parçanın şeklinin ve boyutlarının tekrar tekrar test edilmesi ve işlenmemiş parçanın şeklini ve boyutlarını doğrulamak için sürekli olarak revize edilmesi gerekir.
3.2 Keskin Bükümlü Bileşenler için Boşluk Geliştirme Boyutlarının Hesaplanması (r<0,5t)
Bir bileşenin bükülme yarıçapı r 0,5t'den az olduğunda, bu keskin bir bükülme olarak adlandırılır. Bu tür bileşenler için boş geliştirme boyutunun hesaplanması, bükülmeden önce ve sonra hacim tutarlılığı ilkesine dayanır.
Keskin bükümlerde, bükümdeki malzemenin ciddi şekilde incelmesi nedeniyle deformasyon süreci son derece karmaşıktır, bu da işlenmemiş parça geliştirme boyutlarının doğru bir şekilde hesaplanmasını zorlaştırır. Bu nedenle, hesaplanan işlenmemiş parça geliştirme boyutlarının ampirik verilere dayalı olarak veya deneme bükme yoluyla düzeltilmesi gerekir.
Keskin büküm bileşenlerinin (r<0,5t, φ=90°) işlenmemiş parça geliştirme boyutları için hesaplama formülü Tablo 5-3'te bulunabilir.
Tablo 5-3 Keskin büküm bileşenlerinin boşluk geliştirme boyutları için hesaplama formülü (r<0,5t, φ=90°) (birim: mm)
| Seri Numarası | Bükme Özellikleri | Şematik | Formül |
| 1 | Köşeyi bük. |  | L=a+b+0.4t |
| 2 | Düzleştir. |  | L=a+b-0.43t |
| 3 | İki köşeyi aynı anda bükün. | 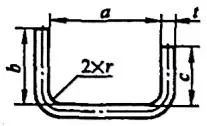 | L=a+b+c+0.6t |
| 4 | Üç köşeyi aynı anda bükün. | 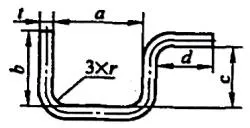 | L=a+b+c+d+0,75t |
| 5 | İlk seferde iki köşeyi bükün ve ikinci seferde başka bir köşeyi bükün. | L=a+b+c+d+t | |
| 6 | Dört köşeyi aynı anda bükün. | 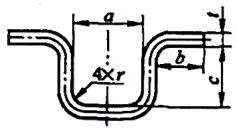 | L=a+2b+2c+1.2t |
| 7 | İki durumda dört köşe oluşturacak şekilde bükün. | L=a+2b+2c+1.2t |
3.3 Menteşe Tipi Bükme Parçaları için Katlanmamış Boyutların Hesaplanması
Menteşe tipi için bükme parçalari r= (0,6~3,5)t ile (Şekil 5-10'a bakınız), flanşlama işlemi genellikle Şekil 5-11'de gösterilen modeli takip eder. Flanşlama sırasında sac metalin kalınlığı artar ve nötr tabaka dışa doğru kayar. İşlenmemiş parçanın katlanmamış boyutları aşağıdaki formülle yaklaşık olarak hesaplanabilir:
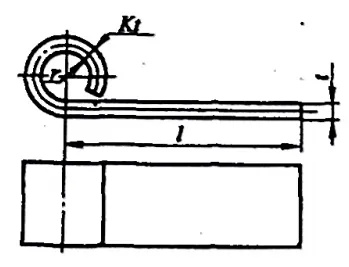
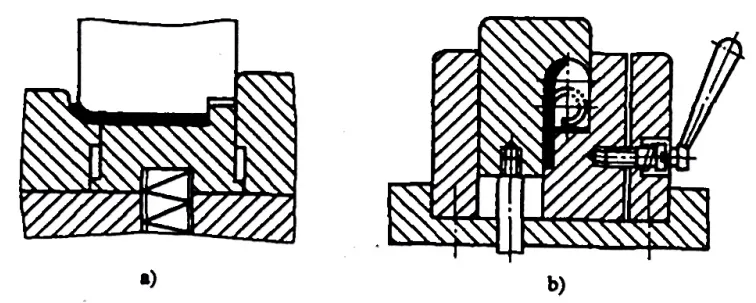
- a) İlk operasyon
- b) İkinci operasyon
L=l+1.57π(r+Kt)+r
Nerede?
- L - Boşluğun katlanmamış boyutları (mm);
- l - Düz segmentin uzunluğu (mm);
- r - İşlenmemiş parçanın iç bükülme yarıçapı (mm);
- K - Nötr katmanın yer değiştirme katsayısı. r/t=0.5~1.8 olduğunda, K genellikle 0.5~0.70 olarak alınır (r/t değeri ne kadar küçükse, K değeri o kadar büyüktür; tersine, K değeri o kadar küçüktür). Tablo 5-4'e göre de seçilebilir.
Tablo 5-4 Menteşe Tipi Bükme Parçaları için Nötr Katmanın Yer Değiştirme Katsayısı
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |