Sac metal bileşen geliştirme çiziminin oluşturulması sürecinde, işleme malzemesinin kalınlığının etkisini de göz önünde bulundurmak, yani uygun plaka kalınlığı ayarlamalarını yapmak gerekir.
Genel olarak, kalınlığı 3 mm'den az olan sac malzemeler için plaka kalınlığı ayarına gerek yoktur. Sac malzemenin merkezi çapına göre veya iç ve dış yüzey kesim hatlarına göre hesaplanabilir. Şekillendirme sonrası boyutlar izin verilen sapma aralığı içindedir. Levha kalınlığı 3 mm'den büyük olduğunda, sac malzemenin merkezi çapına göre hesaplanmalıdır. Tanımlama kolaylığı için, aşağıdaki geliştirilmiş malzemeler için hesaplamalar, sac malzemenin merkezi çapına atıfta bulunur.
1. Silindirik Kabukların Gelişim Hesaplaması
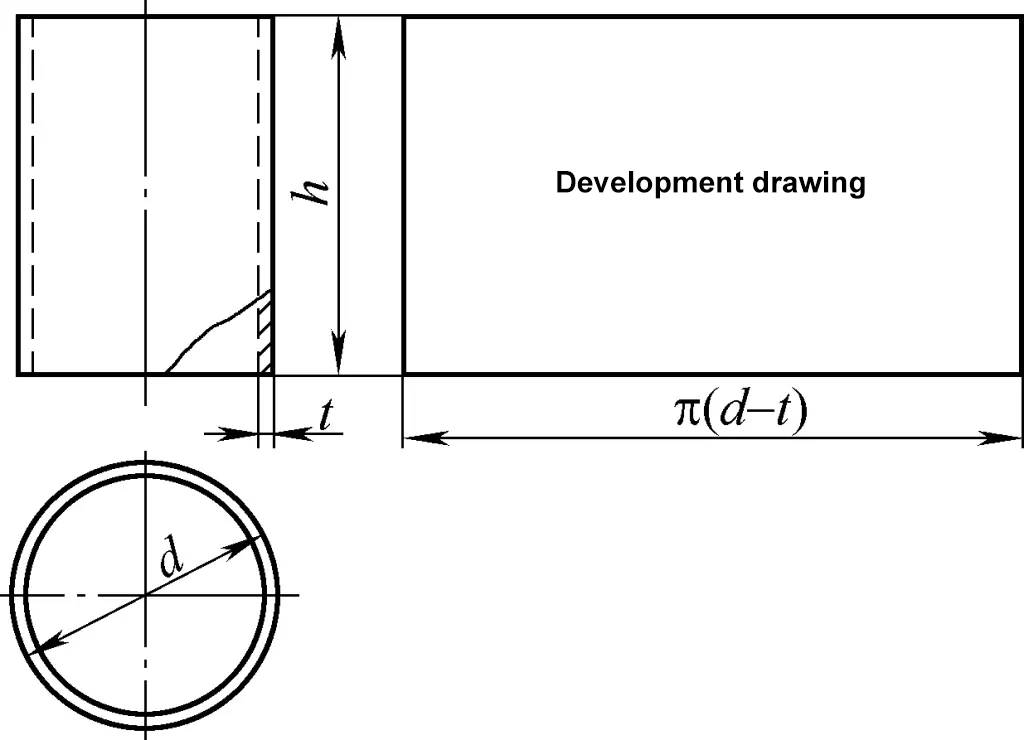
Silindirik kabuk silindirik yüzeye aittir ve gelişim çizimi bir dikdörtgendir. Dikdörtgenin bir kenarı silindirin çevresine π(d-t) eşittir ve diğer kenarı Şekil 1'de gösterildiği gibi silindirin h yüksekliğidir. Şekilde, d silindirin dış çapı ve t plaka kalınlığıdır.
2. Dik Dairesel Konilerin Gelişim Hesaplaması
Sağ dairesel koninin gelişim çizimi bir sektör yayıdır. Şekil 2'de gösterilen sağ dairesel koninin gelişim çizimi için hesaplama formülü şöyledir:
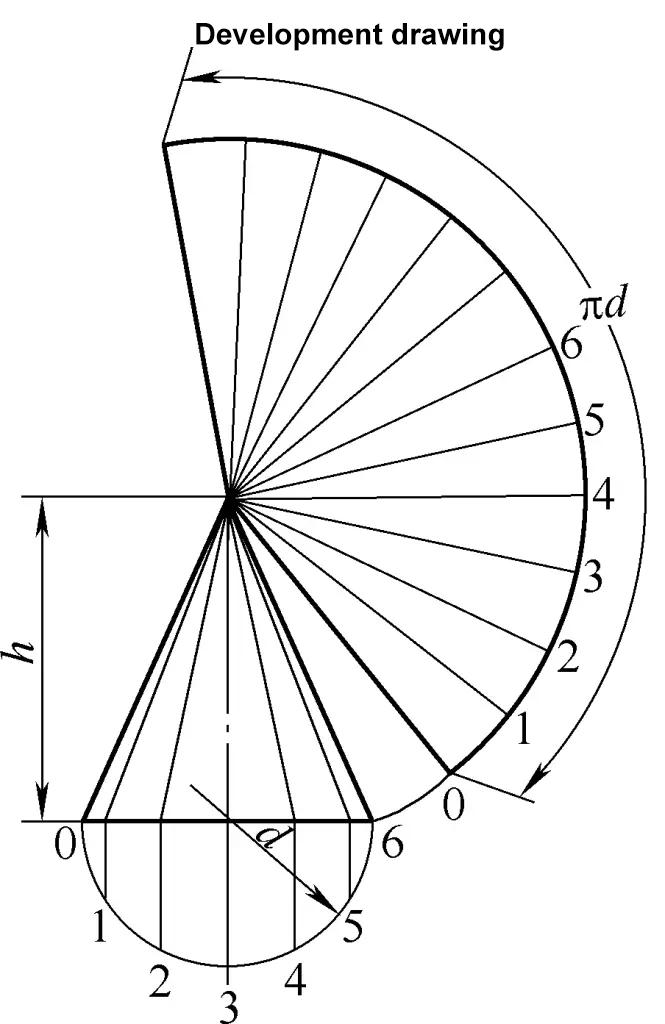
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
Formülde
- R - Sektör yayının yarıçapı (mm);
- α - Sektör açısı (°);
- L - Sektör yayının akor uzunluğu (mm).
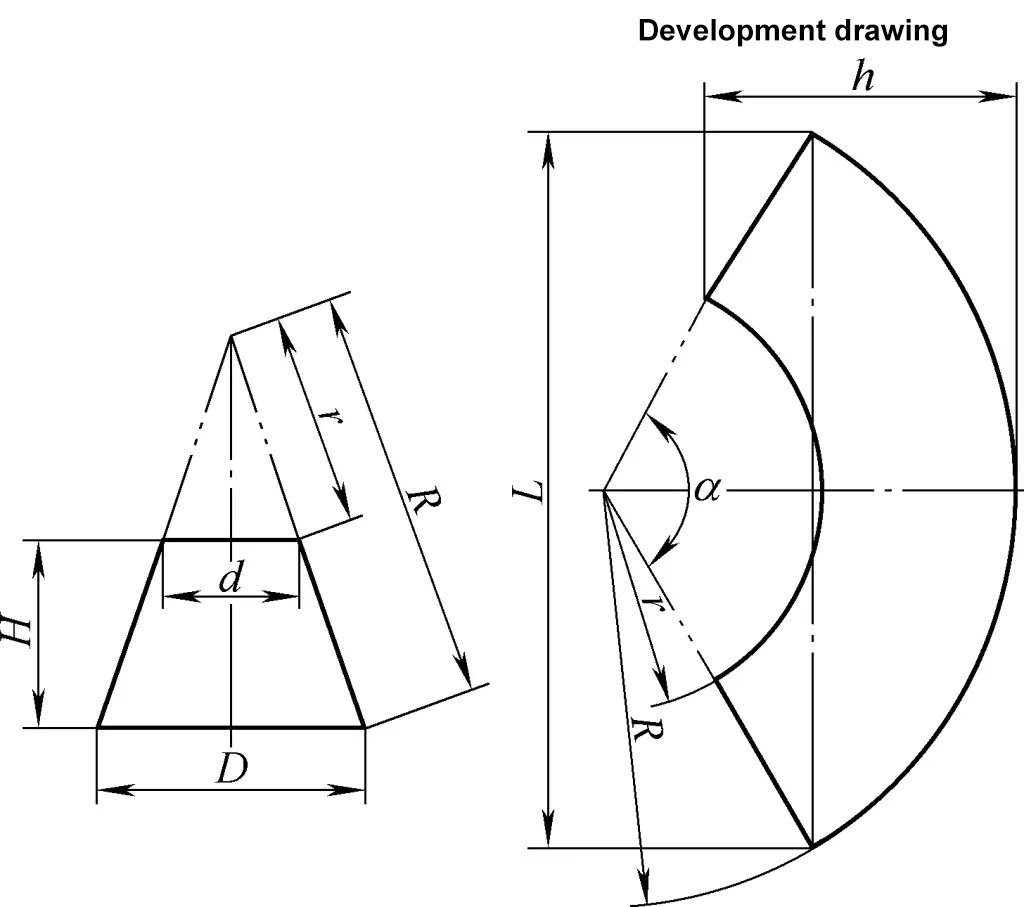
3. Kesik Dik Dairesel Konilerin Gelişim Hesaplaması
Kesik dik dairesel koninin gelişim çizimi eşmerkezli bir sektör yayıdır. Şekil 3'te gösterilen kesik dik dairesel koninin gelişim çizimi için hesaplama formülü şöyledir:
R=√{(D/2)2+[DH/(D-d)]2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
α>180° olduğunda, h=R+rsin[(α-180)/2]
Formüldeki sembollerin anlamları için Şekil 3'e bakınız.
4. Eğik Dik Dairesel Konilerin Gelişim Hesaplaması
Eğik sağ dairesel koninin gelişim çizimi düzensiz bir sektör yayıdır. Şekil 4'te gösterilen eğik sağ dairesel koninin gelişim çizimi için hesaplama formülü şöyledir:
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[(A-D/2cosαn)2+(D/2)2günah2αn+H2]
yn=fn(1-h/H)
m=Dsin(180°/n )
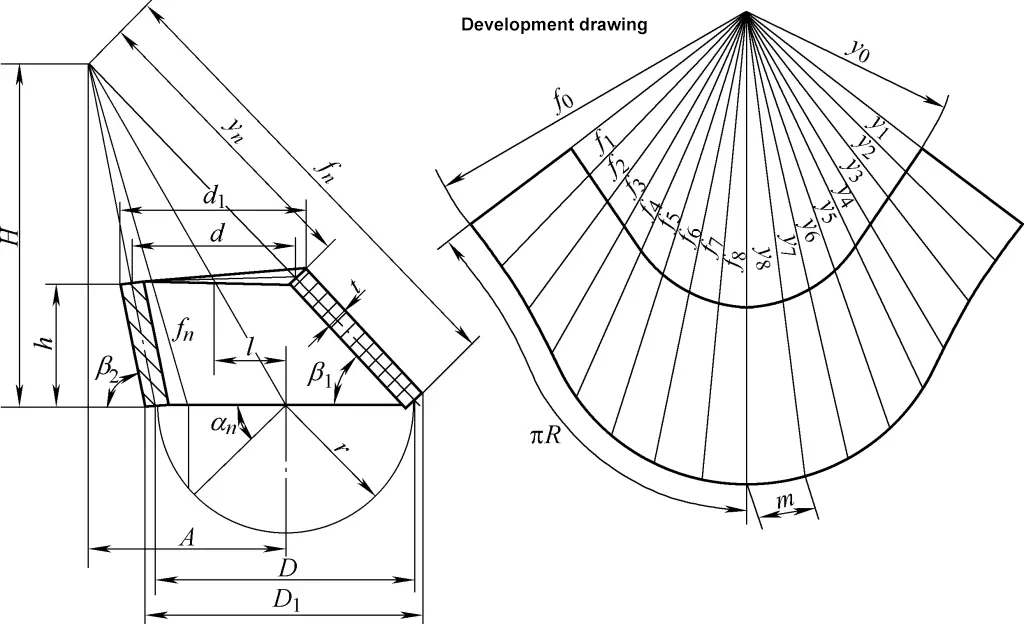
Formülde
- D1, d1 - Büyük ve küçük uçların dış çapları (mm);
- D, d - Büyük ve küçük uçların merkezi çapları (mm);
- h - Merkezi yükseklik (mm);
- l - Eksantrik mesafe (mm);
- n - Çevre etrafındaki bölme sayısı; bölme sayısı arttıkça hesaplama daha karmaşık ancak çizim daha doğru olur. Genel olarak, bölme sayısı Tablo 1'de referans alınabilir;
- fn, yn - Eğik dik dairesel koninin eğik çizgilerinin uzunlukları (mm).
Tablo 1 Sac Metal Geliştirmeleri için Bölüm Sayısı
| Geliştirilen Parçanın Yarıçapı/mm | Bölüm Sayısı |
| 50 içinde | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| 2000'in üzerinde | 96 |
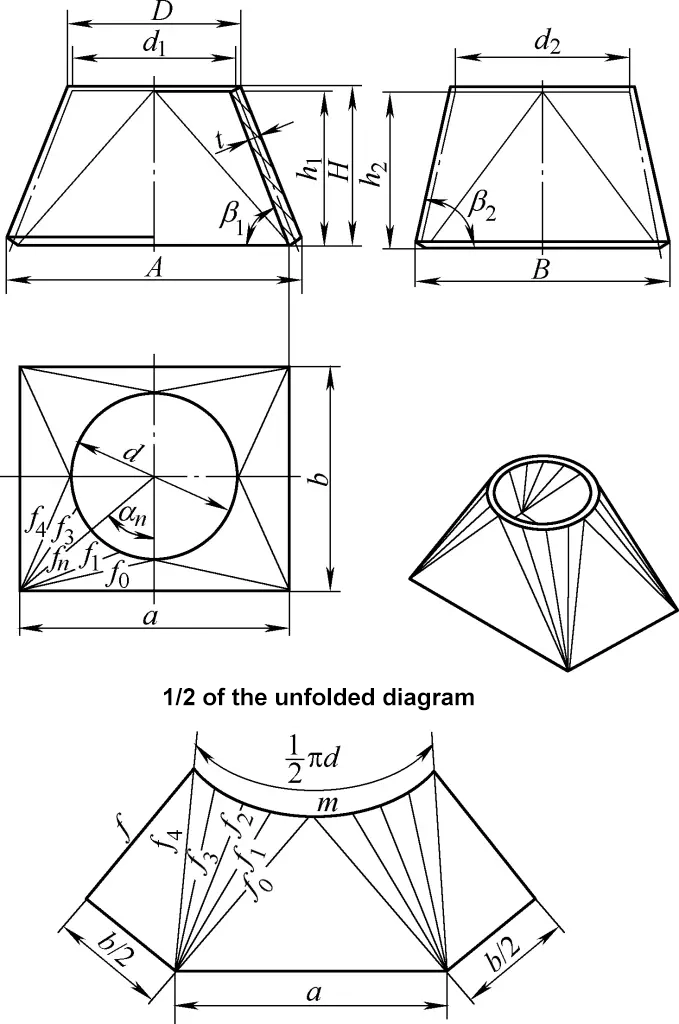
5. Ortokonik Dikdörtgenden Yuvarlak Geçiş Kanalının Geliştirme Hesaplaması
Şekil 5'te gösterilen ortokonik dikdörtgen-yuvarlak geçiş kanalı dört eşit eğik dik dairesel konik yüzey ve dört simetrik üçgen düzlemden oluşmaktadır. Geliştirme çizimi için hesaplama formülü şöyledir:
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(0<α<90° olduğunda)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(α=90° olduğunda)
f=1/2√[(a-d)2+4h12]
m=πd/n
Formüldeki sembollerin anlamları için Şekil 5'e bakınız ve n, çevre etrafındaki bölümlerin sayısıdır. Genel olarak, Tablo 1'deki bölme sayısı hesaplama gereksinimlerini karşılayabilir.