La forza di piegatura è una base importante per la progettazione dei processi di stampaggio, la scelta delle presse e la progettazione degli stampi.
Poiché l'entità della forza di piegatura è legata non solo alle dimensioni dello spezzone, alle proprietà meccaniche del materiale, alla distanza tra i supporti dello stampo, al raggio di curvatura e alla distanza tra gli stampi, ma anche al metodo di piegatura, è difficile eseguire calcoli accurati utilizzando metodi di analisi teorica. Pertanto, nella produzione, le formule empiriche elencate nella Tabella 1 sono solitamente utilizzate per un calcolo approssimativo della forza di piegatura.
I. Basi teoriche e metodi di calcolo per la forza di flessione
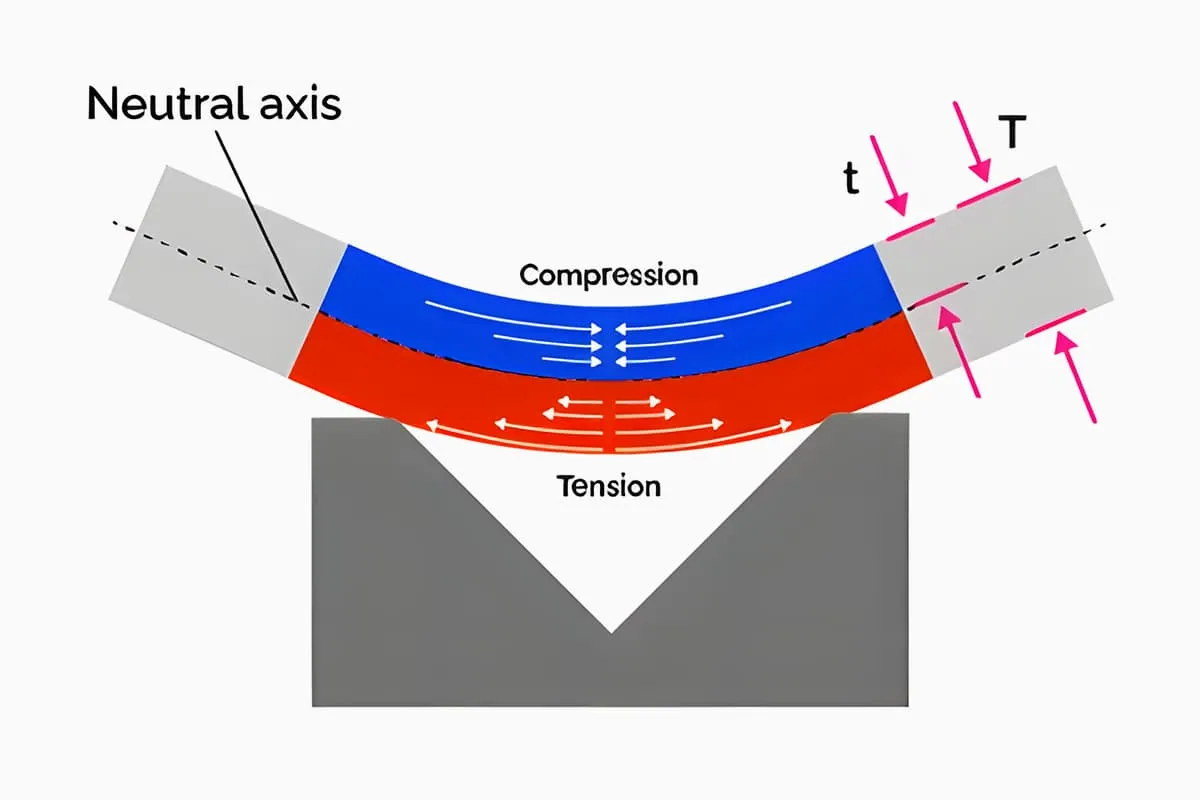
Il metodo di calcolo teorico della forza di flessione è derivato nelle condizioni di equilibrio statico in cui la somma delle varie forze esterne che agiscono sullo spezzone in flessione è pari a zero e la coppia esterna che agisce sullo spezzone in flessione è uguale alla sua coppia di resistenza interna, attraverso il calcolo convenzionale.
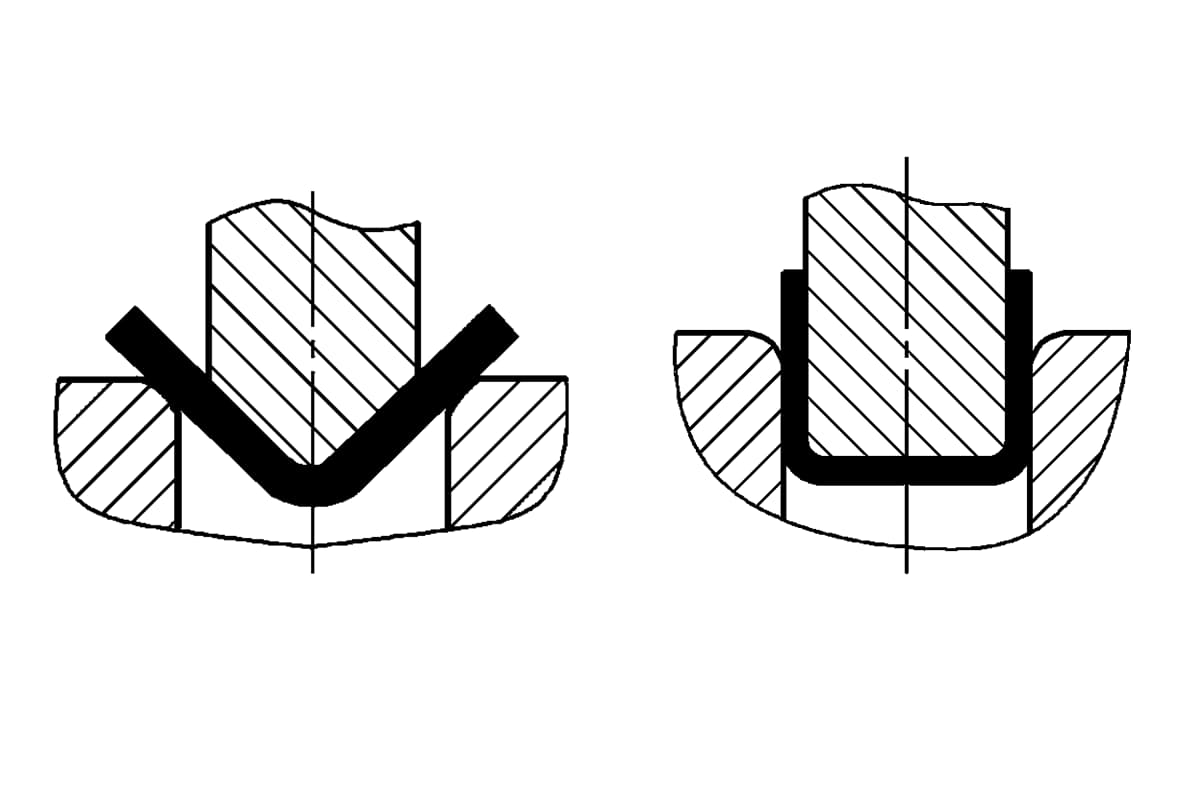
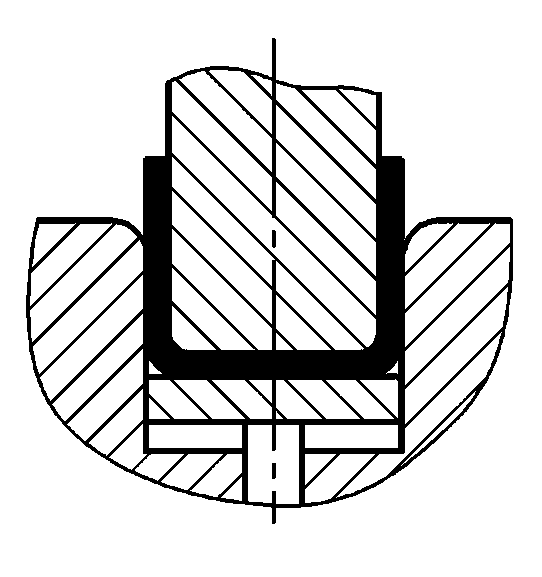
Il metodo di piegatura e la struttura dello stampo modificano lo stato di sollecitazione dello spezzone piegato. Metodi di piegatura diversi danno luogo a pressioni di piegatura molto diverse. Se si considerano le forme a V e a U comunemente utilizzate parti di piegatura come esempi, come mostrato nella Figura 1, possono essere formati mediante piegatura con stampi di piegatura ordinari in acciaio pieno, utilizzando rispettivamente la piegatura libera, la piegatura con ribaltamento a contatto e la piegatura con correzione dell'impatto.
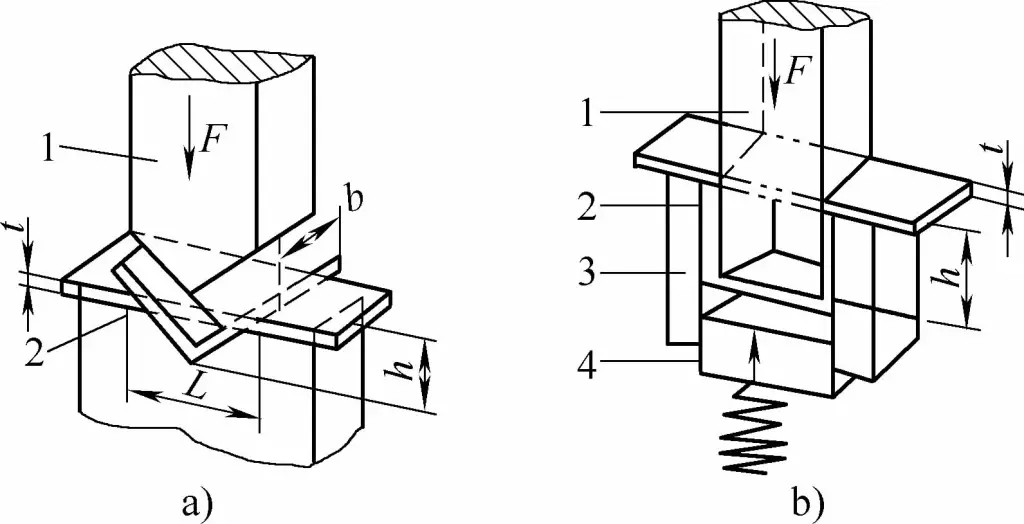
- a) Elementi di piegatura a V
- b) Elementi di piegatura a U
- 1 - Punzone di piegatura
- 2 - Parte di piegatura
- 3 - Stampo di piegatura a U
- 4 - Strumento superiore
- L - Larghezza dell'apertura dello stampo a U
- t - Spessore della parte in flessione
- h - Profondità della cavità dello stampo di piegatura a V
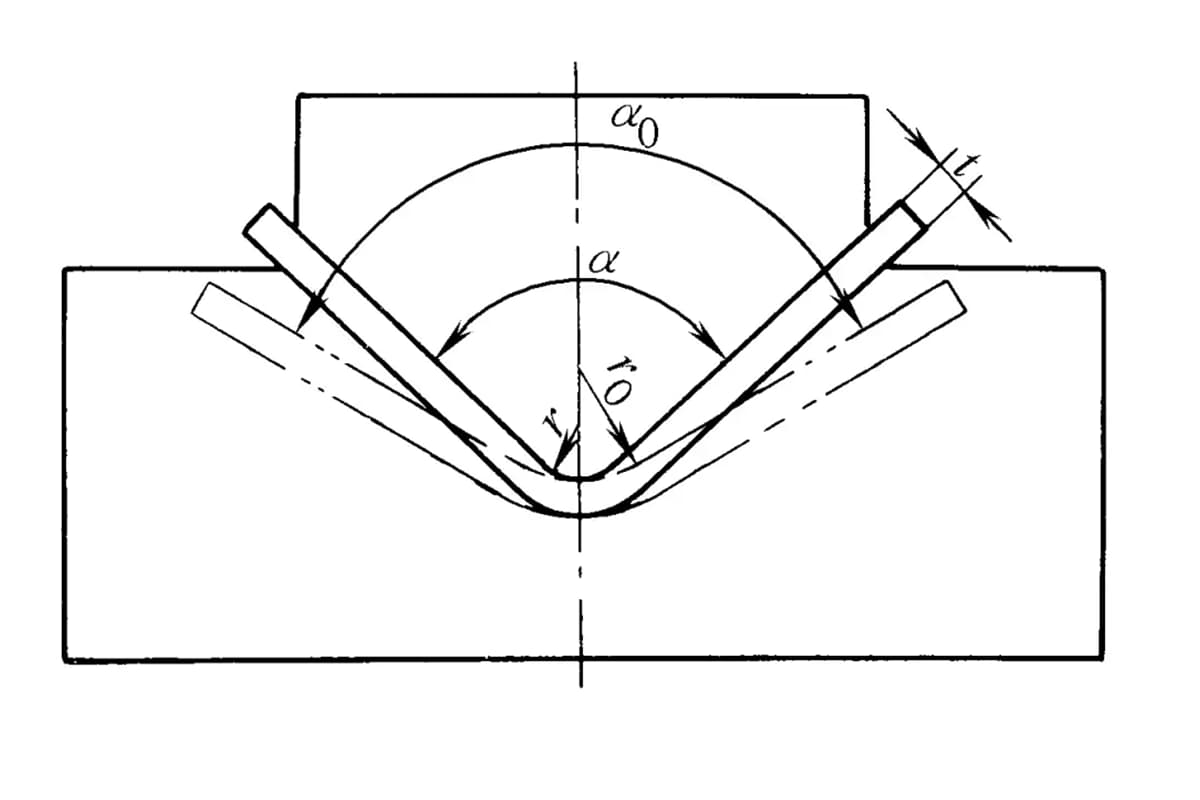
I pezzi di piegatura a V utilizzano un carico concentrato al centro di due supporti di un pezzo grezzo piatto per la piegatura pura e la piegatura libera, utilizzata soprattutto nei cantieri. I pezzi di lamiera piegati online, di piccole e medie dimensioni, sono per lo più formati con la piegatura a contatto, mentre i pezzi di lamiera ad alta resistenza e di medio spessore sono spesso piegati su presse a frizione utilizzando la piegatura a correzione d'urto. La piegatura libera richiede una pressione minore, senza pressione aggiuntiva, solo una semplice forza di piegatura.
II. Calcolo della forza di flessione con vari metodi di flessione
Le formule di calcolo della forza di flessione con i vari metodi di flessione sono riportate nella Tabella 1.
Tabella 1 Formule di calcolo della forza di flessione con vari metodi di flessione
| Nome | Schema | Caratteristiche della deformazione a flessione | Formula di calcolo della forza di flessione | ||
| Teorico | Approssimativo | Consigliato | |||
| Curvatura libera ad angolo singolo (parte di piegatura a V) | 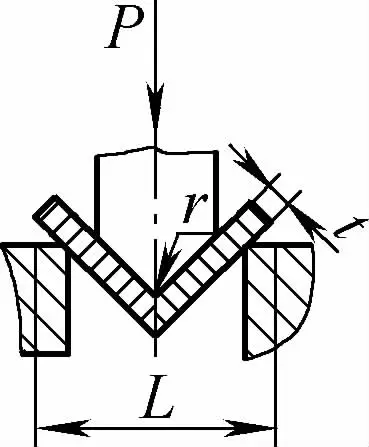 | Lo spezzone viene piegato al centro esercitando una pressione su due supporti all'ingresso dello stampo; la parte inferiore non entra in contatto con lo stampo. | Quando 2r≤L, F=0,7bt3 Rm /(r+t) Quando 2r>L, F=2bt2 Rm /3L | F = KbtRm | F=Cbt2Rm/L |
| Curvatura a contatto monoangolare (parti di piegatura a V) | 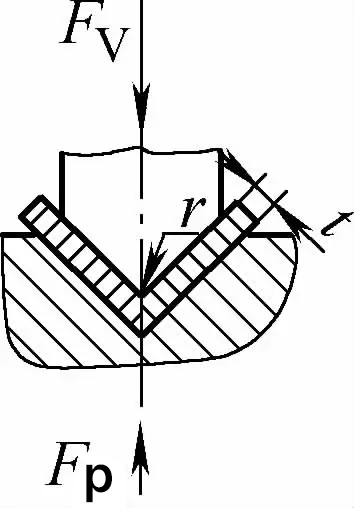 | Prima che il processo di piegatura sia completato, lo spezzone di piegatura è a stretto contatto con l'intera cavità dello stampo. In genere si utilizza una piastra di pressione per rendere la curvatura gap del dado maggiore o uguale a t | Quando 2r≤L, Fv =0,7bt2 Rm /(r+t)+Fp Quando 2r>L, Fv =2bt2 Rm /3L+Fp | Fv=KbtRm +Fp | Fv=2Cbt2Rm/L |
| Contatto monoangolare con piegatura a correzione d'urto (parti di piegatura a V) | 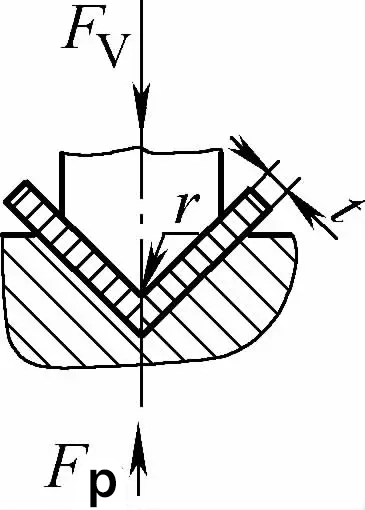 | Basato sulla piegatura a contatto, ha anche la funzione di correzione dell'impatto. La distanza tra gli stampi di piegatura è generalmente inferiore o uguale a t | Fv=0,7bt2Rm/L+Fp+qAb | Fv=1,3qAb | Fv=1,39qAb |
| Curvatura libera a doppio angolo (parti piegate a U) | 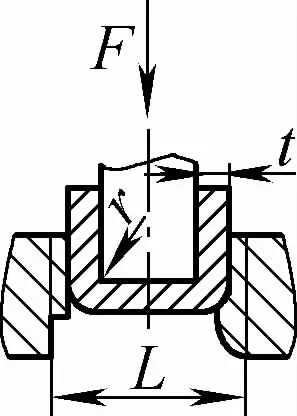 | Lo spezzone di piegatura viene piegato al centro applicando una pressione su due supporti all'ingresso dello stampo; la parte inferiore dello spezzone non entra in contatto con lo stampo. | Quando 2r≤L, F=0,7bt 2 Rm /(r+t) Quando 2r>L, F=2bt 2 Rm /3L | F =KbtRm | F=0,4CKbtRm |
| Piegatura a contatto a doppio angolo (parti piegate a U) | 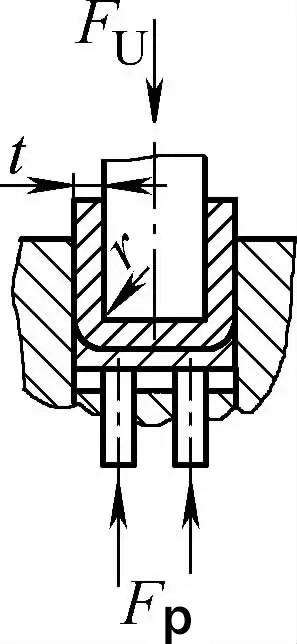 | Durante la piegatura, si utilizza una piastra di pressione o una distanza pari o leggermente superiore a t, ma non vi è alcuna funzione di correzione dell'impatto. | Quando 2r≤L, Fu =0,7bt2Rm /(r+t)+Fp Quando 2r>L, Fu =2bt2Rmn/3L+Fp | Fu =KbtRm +Fp | Fu=0,5CbtRm |
| Contatto a doppio angolo con piegatura a correzione d'urto (parti piegate a U) | 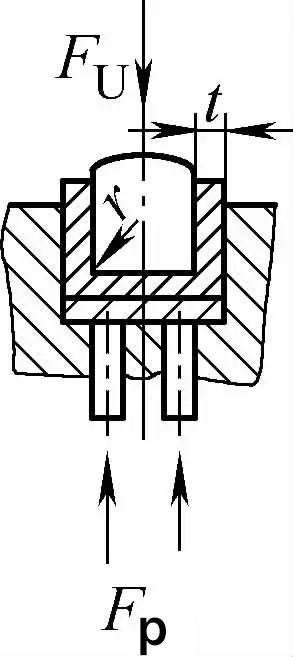 | Durante la piegatura, una distanza di piegatura inferiore o uguale a t viene utilizzata con una piastra di pressione (piastra superiore) e ha anche la funzione di correzione dell'impatto. | Fu=0,7bt2Rmn/L+Fp+qAb | Fu=1,3qAb | Fu=1,3qAb |
Nota: il significato dei simboli della tabella è il seguente:
- b - larghezza della parte in flessione (mm);
- R - resistenza alla trazione del materiale della parte piegata (MPa);
- L - lunghezza dello spezzone di piegatura nei punti di appoggio su entrambi i lati dell'apertura dello stampo di piegatura (mm);
- C - coefficiente, per flessione ad angolo singolo L>10t, C=1; per flessione ad angolo doppio r=t, C=1; n-numero di angoli di flessione (pezzi);
- A - area di appoggio della parte in flessione (mm²);
- F - pressione di correzione piatta (kN), generalmente 30%~100% della forza di flessione;
- K - coefficiente del tipo di materiale; il valore è riportato nella Tabella 2;
- q - pressione unitaria (d'urto) di correzione (MPa), il cui valore è riportato nella Tabella 3.
Tabella 2 Tipo di materiale coefficiente K
| Materiale | Rapporto L/t | |||||
| 3 | 10 | 15 | 20 | 25 | 30 | |
| 10 acciaio, 15 acciaio, ottone, alluminio (morbido) | 0.23 | 0.18 | 0.12 | 0.09 | 0.073 | 0.060 |
| 20 acciaio, 25 acciaio, alluminio temprato | 0.21 | 0.17 | 0.11 | 0.08 | 0.070 | 0.057 |
| Acciaio 20, acciaio 25, acciaio 40, alluminio superduro | 0.20 | 0.16 | 0.10 | 0.08 | 0.065 | 0.053 |
Tabella 3 Valore approssimativo della pressione unitaria (d'impatto) di correzione q durante la flessione (unità: MPa)
| Materiale | Spessore del materiale di piegatura t/mm | |
| ≤3 | >3~10 | |
| Alluminio | 30~40 | 50~60 |
| Ottone | 60~80 | 80~100 |
| 10 acciaio, 15 acciaio, 20 acciaio | 80~100 | 100~120 |
| 25 acciaio, 30 acciaio, 35 acciaio | 100~120 | 120~150 |
Formule per il calcolo della forza di flessione
Tabella 4 Formule empiriche per il calcolo della forza di flessione
| Metodo di piegatura | Schema | Formule empiriche | Note |
| Curvatura libera | 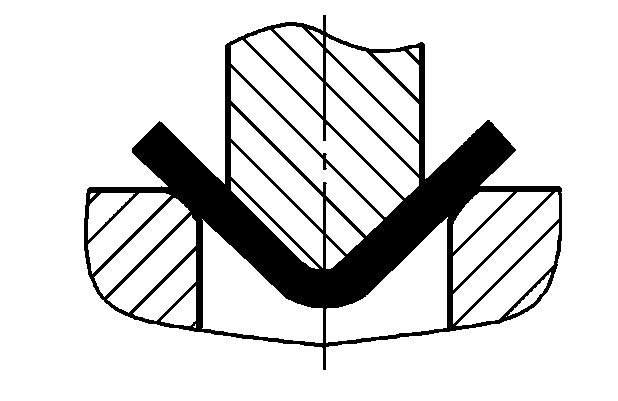 | P=(0,8Bt2σb)/(r+t) | dove P-Forza di flessione totale (N) B-Larghezza della parte piegata (mm) t-Spessore del materiale (mm) σb-Resistenza alla trazione (MPa) r-interno raggio di curvatura (mm) Area di proiezione della parte di correzione A (mm)2 ) Pressione di correzione unitaria (MPa); per il suo valore si veda la Tabella 5. |
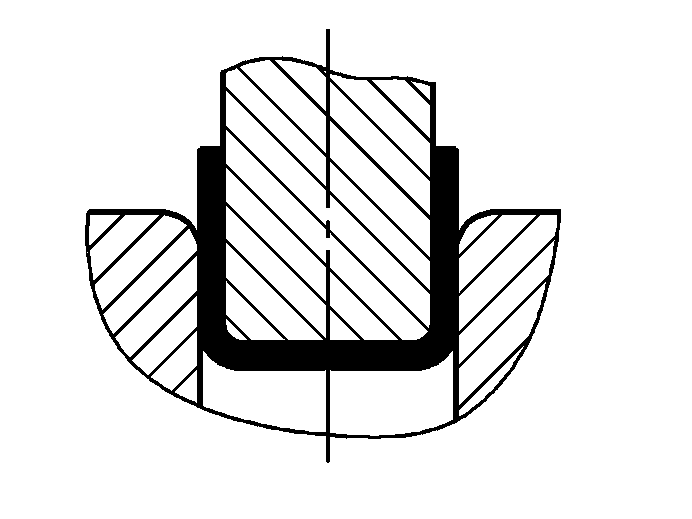 | P=(0,9Bt2σb)/(r+t) | ||
| Piegatura con correzione | 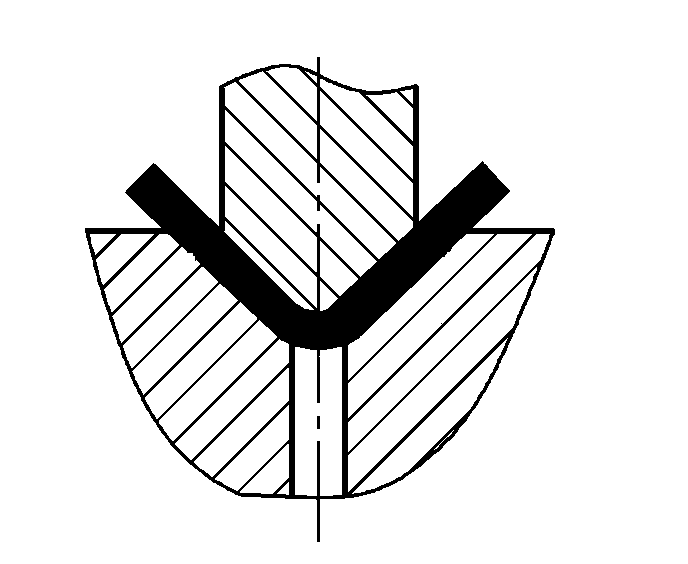 | P=(1,4Bt2σb)/(r+t) | |
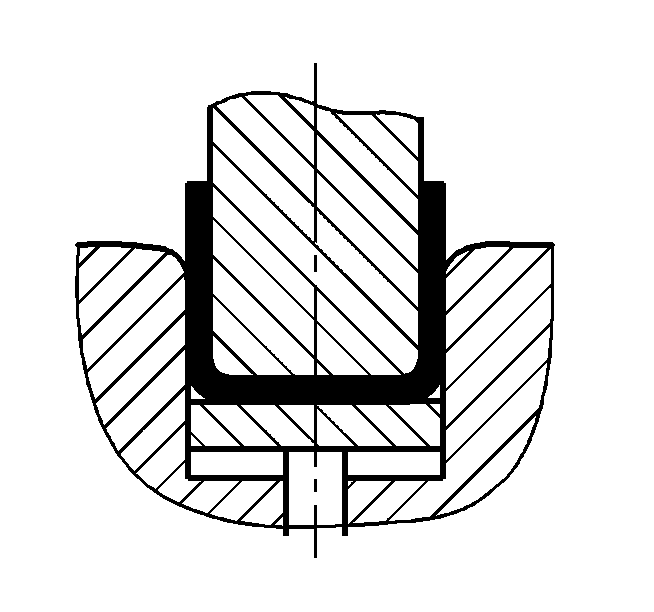 | P=(1,6Bt2σb)/(r+t) | ||
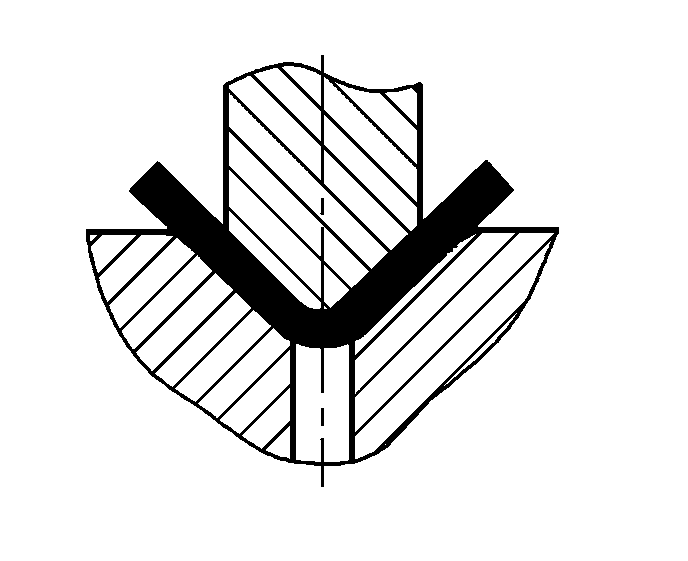 | P=(1,4Bt2σb)/(r+t)+Aq | ||
 | P=(1,6Bt2σb)/(r+t)+Aq |
Tabella 5 Valore unitario della pressione di correzione q (unità: MPa)
| Materiale | Spessore del materiale / mm | |||
| <1 | 1~3 | 3~6 | 6~10 | |
| Alluminio | 15~20 | 20~30 | 30~40 | 40~50 |
| Ottone | 20~30 | 30~40 | 40~60 | 60~80 |
| Acciaio 10~20 | 30~40 | 40~60 | 60~80 | 80~100 |
| 25~30 acciaio | 40~50 | 50~70 | 70~100 | 100~120 |
III. Calcolo del lavoro di flessione
Il lavoro di piegatura delle parti piegate a V può essere calcolato con la seguente formula.
Wv=mFvh
Dove
- Wv - Lavoro di piegatura dei pezzi a V (J), generalmente calcolato con la piegatura a contatto;
- m - Coefficiente di correzione, m=0,32 per le parti in flessione a V, m=0,63 per le parti in flessione a U;
- Fv - Forza di flessione degli elementi di flessione a V (kN), F v o F u Per calcolare la forza di flessione si può utilizzare la formula di calcolo appropriata riportata nella Tabella 1.
- h - Profondità della cavità dello stampo di piegatura (cioè la corsa di piegatura) (mm), h può essere calcolato anche con la seguente formula.
h=0,5L~0,4(t+r)
Dove
- L - Distanza tra i due punti di appoggio degli elementi di piegatura a V sull'apertura dello stampo di piegatura (mm);
- t - Spessore delle parti piegate (mm);
- r - Raggio di curvatura (mm).
IV. Metodo grafico semplificato per la forza di flessione e il lavoro di flessione
La Figura 2 mostra il grafico della colonna di calcolo per la forza di flessione e il lavoro di flessione dei pezzi piegati a V e a U. Questa tabella è comoda da usare, il calcolo grafico è rapido e i risultati sono vicini alla realtà, adatti all'uso in loco.
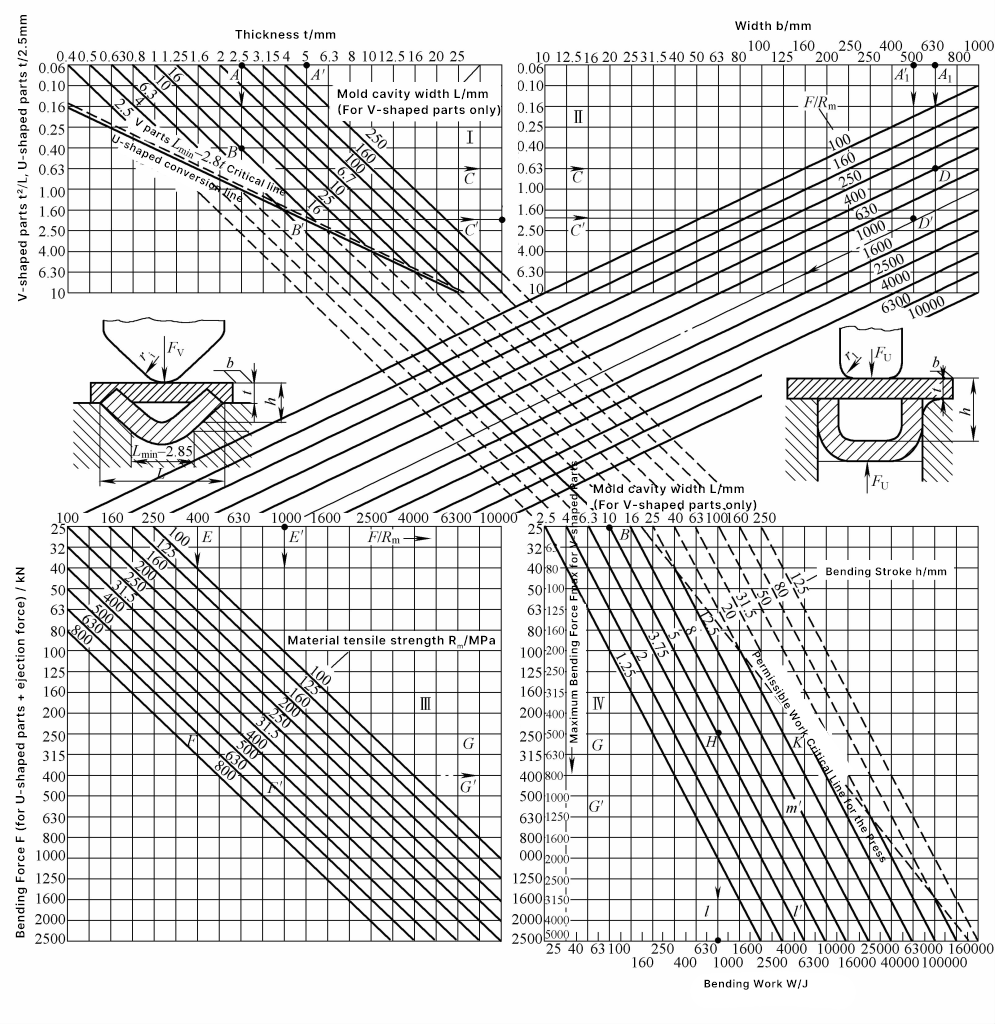
Nota: i simboli della tabella indicano quanto segue:
- F - Forza di flessione degli elementi di flessione a V e a U (kN);
- W - Lavoro di piegatura di elementi di piegatura a V e a U (J);
- H - Corsa di lavoro di piegatura degli elementi di piegatura a V e a U (mm);
- L, L min - Larghezza di apertura dello stampo di piegatura per pezzi piegati a V (mm), larghezza minima di apertura (mm);
- r - Raggio interno di curvatura delle parti piegate (mm);
- t - Spessore delle parti piegate (mm).
Esempio di calcolo grafico. Dato un pezzo da piegare a V con t=2,5 mm, larghezza di apertura dello stampo di piegatura L=10 mm. Nell'area I della Figura 2, t2/L=0,63 (vedi linea ABC). Data la larghezza della parte in flessione b=630 mm, la resistenza alla trazione del materiale R m =630MPa, nelle aree II e III, trovare il valore A1 DEF, e nell'area III, lungo la linea di estensione destra, si trova la linea FG, che determina una forza di flessione Fv =250kN.
Nell'area IV, considerando la pressione di raddrizzamento, la pressione totale è F∑ =2F=500kN. La corsa di lavoro di flessione h=0,5L=5mm, il coefficiente di correzione m=0,32, quindi il lavoro di flessione Wv =mF∑ h=800J, come mostrato dalla linea BH e dalla linea CHI nella Figura 2.