Buigkracht is een belangrijke basis voor het ontwerpen van stansprocessen, het selecteren van persen en het ontwerpen van matrijzen.
Aangezien de grootte van de buigkracht niet alleen gerelateerd is aan de grootte van de blenk, de mechanische eigenschappen van het materiaal, de afstand tussen de steunen van de matrijs, de buigradius en de ruimte tussen de matrijzen, maar ook sterk gerelateerd is aan de buigmethode, is het moeilijk om nauwkeurige berekeningen uit te voeren met theoretische analysemethoden. Daarom worden bij de productie meestal de empirische formules uit tabel 1 gebruikt voor een ruwe berekening van de buigkracht.
I. Theoretische berekeningsbasis en methoden voor buigkracht
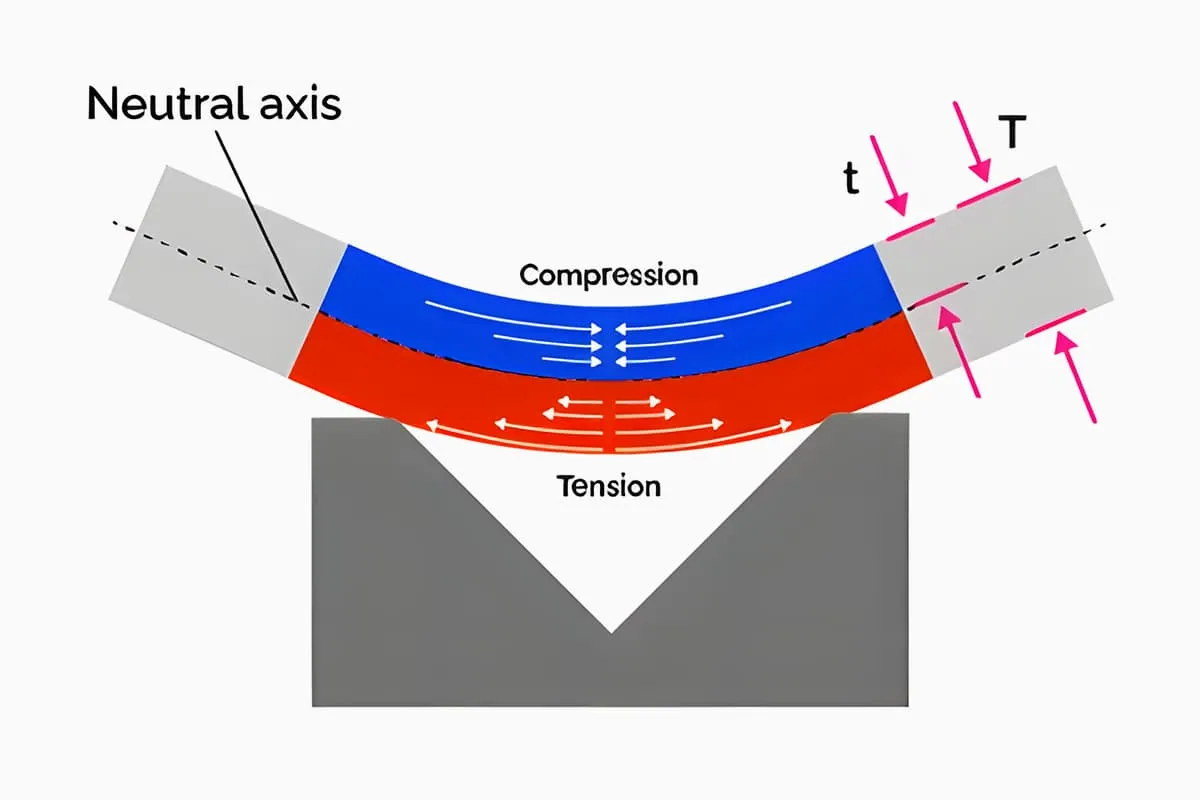
De theoretische berekeningsmethode van de buigkracht wordt afgeleid onder de statische evenwichtsomstandigheden dat de som van verschillende externe krachten die op het buigraam werken nul is, en het externe koppel dat op het buigraam werkt gelijk is aan het koppel van de interne weerstand, door middel van conventionele berekening.
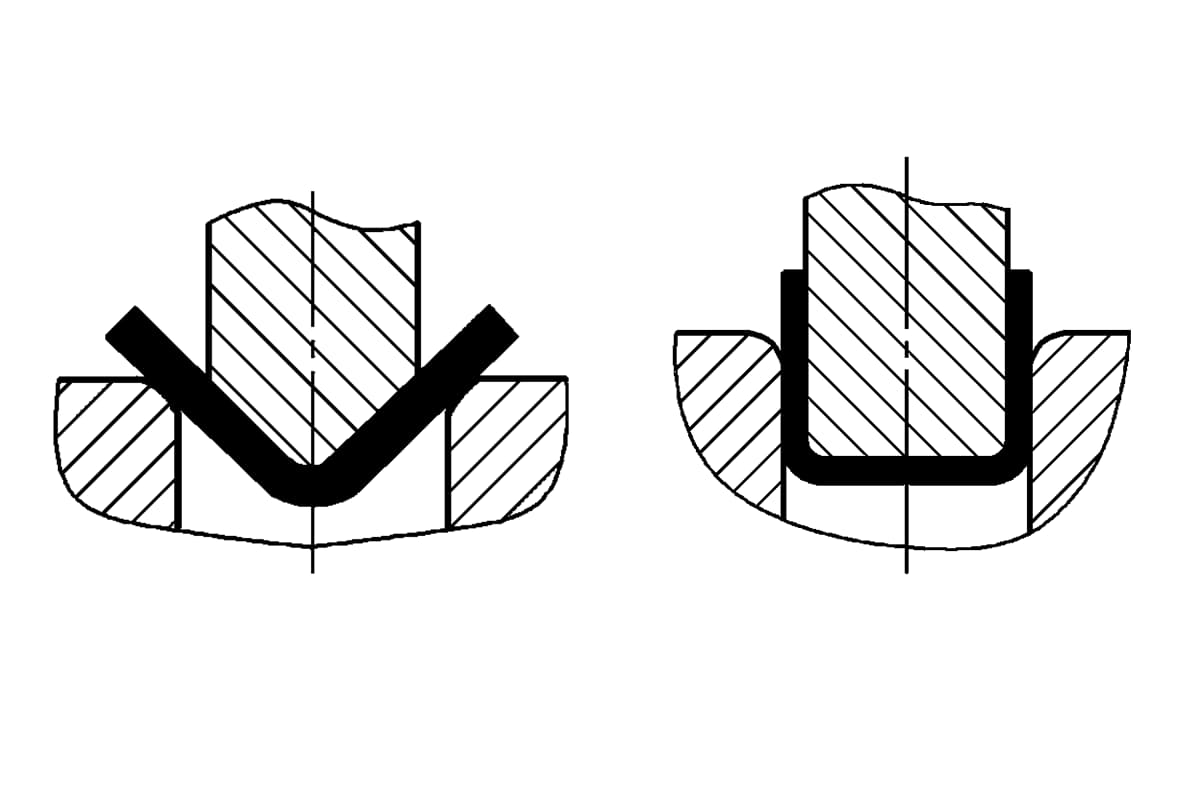
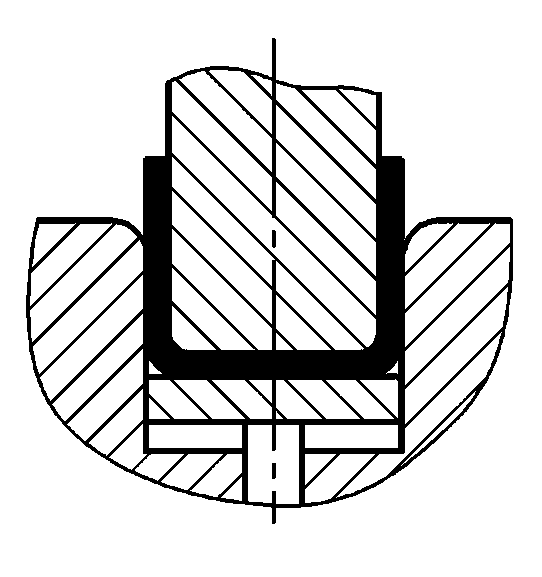
De buigmethode en de matrijsstructuur veranderen de spanningstoestand van de buigblenk. Verschillende buigmethodes resulteren in enorm verschillende buigdrukken. Als we de veelgebruikte V-vorm en U-vorm nemen buigonderdelen als voorbeeld, zoals getoond in figuur 1, kunnen ze worden gevormd door buigen met gewone volstalen buigmatrijzen, respectievelijk door gebruik te maken van vrij buigen, contactopbuigend buigen en buigen met inslagcorrectie.
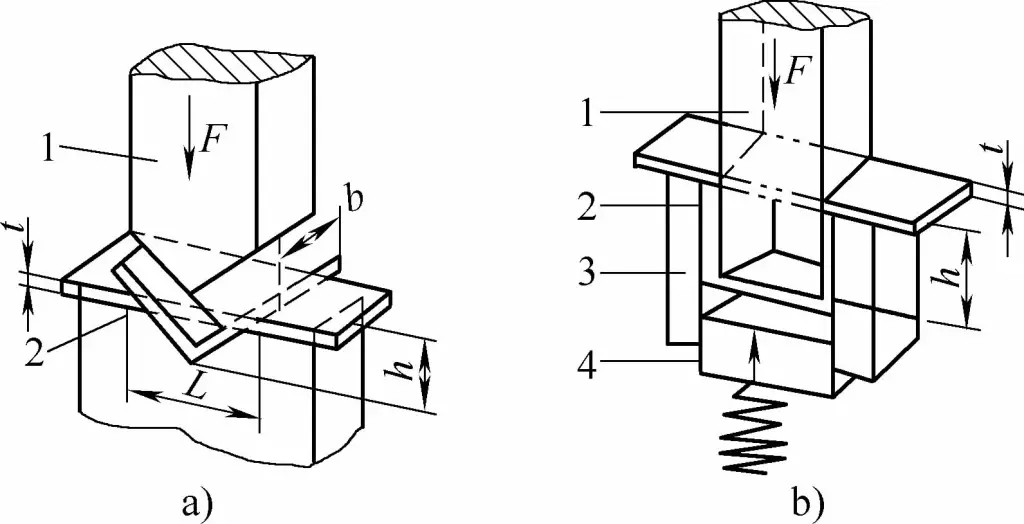
- a) V-vormige buigdelen
- b) U-vormige buigonderdelen
- 1 - Buigstempel
- 2 - Buiggedeelte
- 3 - U-vormige buigmatrijs
- 4 - Top gereedschap
- L - Breedte van U-vormige matrijsopening
- t - Dikte van het buiggedeelte
- h - Diepte van V-vormige buigmatrijsholte
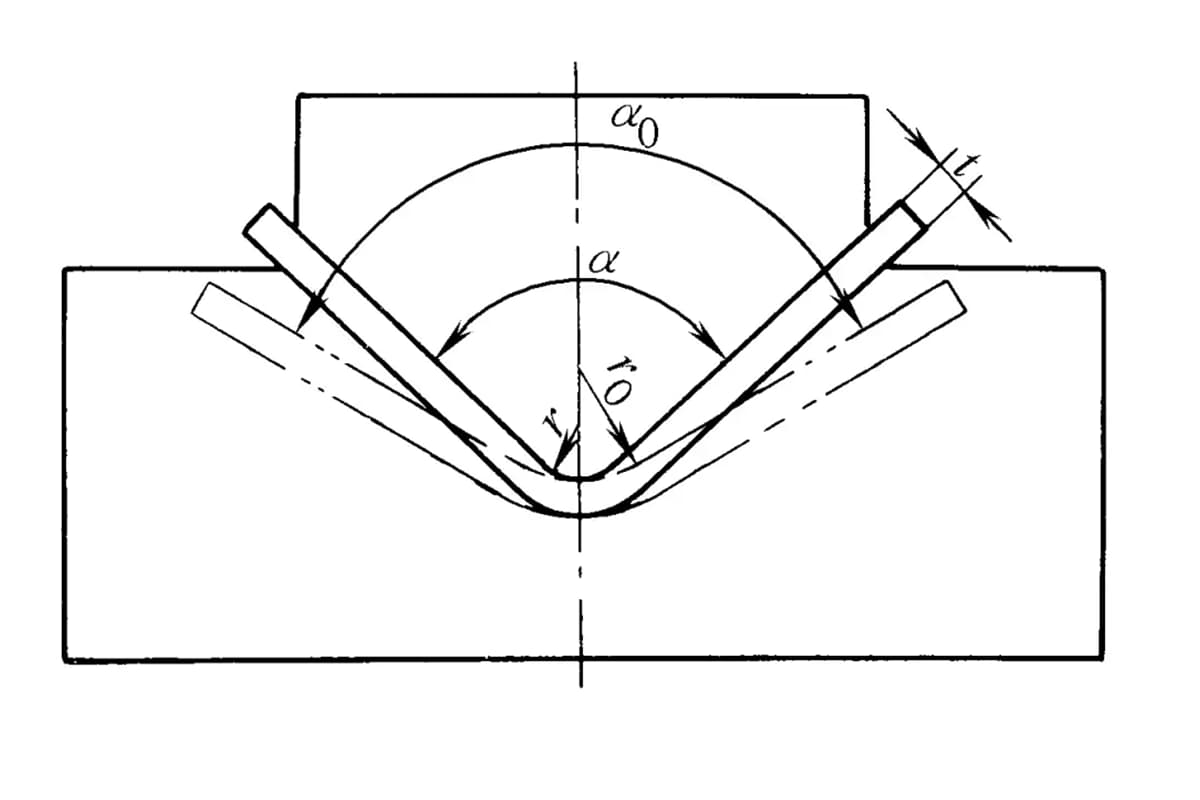
V-vormige buigonderdelen gebruiken een geconcentreerde belasting in het midden van twee steunen van een vlakke plaat voor zuiver buigen en vrij buigen, meestal gebruikt op bouwplaatsen. Online worden kleine en middelgrote plaatbuigonderdelen meestal gevormd door contactbuigen, en plaatbuigonderdelen met een hoge sterkte en gemiddelde dikte worden vaak gebogen op wrijvingspersen met behulp van slagcorrectiebuigen. Vrij buigen vereist minder druk, zonder extra druk, alleen eenvoudige buigkracht.
II. Berekening van buigkracht door verschillende buigmethodes
De berekeningsformules voor buigkracht door verschillende buigmethodes staan in Tabel 1.
Tabel 1 Berekeningsformules voor buigkracht door verschillende buigmethoden
| Naam | Schema | Kenmerken van buigvervorming | Berekeningsformule voor buigkracht | ||
| Theoretisch | Ongeveer | Aanbevolen | |||
| Enkele hoek vrij buigen (V-vormig buiggedeelte) | 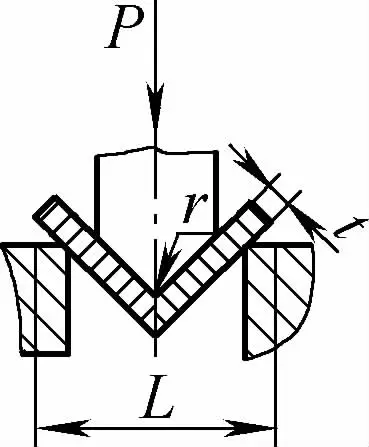 | De blenk wordt in het midden naar beneden gebogen door druk uit te oefenen op twee steunen bij de matrijzeringang, waarbij het onderste deel niet in contact komt met de matrijs. | Wanneer 2r≤L, F=0,7bt3 Rm /(r+t) Als 2r>L, F=2bt2 Rm /3L | F = KbtRm | F=Cbt2Rm/L |
| Buigen met een enkele hoek (V-vormige buigonderdelen) | 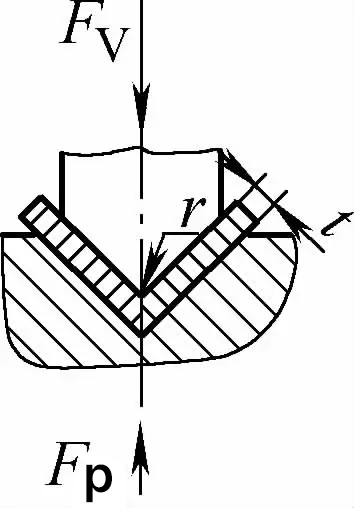 | Voordat het buigproces is voltooid, is de buigblenk in nauw contact met de volledige matrijsholte. Een drukplaat wordt over het algemeen gebruikt om het buigen matrijspleet groter dan of gelijk aan t | Als 2r≤L, Fv =0,7bt2 Rm /(r+t)+Fp Als 2r>L, Fv =2bt2 Rm /3L+Fp | Fv=KbtRm +Fp | Fv=2Cbt2Rm/L |
| Enkele hoek contact met impactcorrectie buigen (V-vormige buigdelen) | 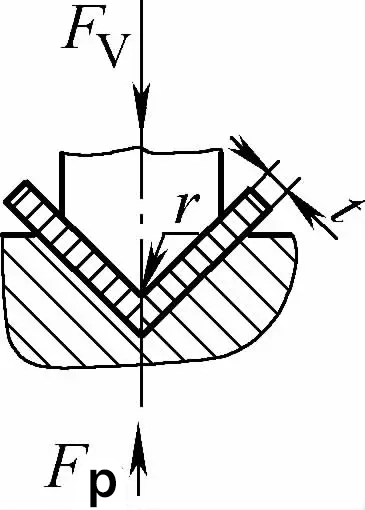 | Gebaseerd op contactbuigen heeft het ook de functie van impactcorrectie. De spleet van de buigmatrijs is over het algemeen kleiner dan of gelijk aan t | Fv=0,7bt2Rm/L+Fp+qAb | Fv=1,3qAb | Fv=1,39qAb |
| Vrij buigen met dubbele hoek (U-vormige buigonderdelen) | 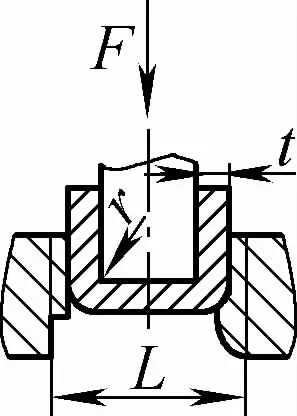 | De buigblenk wordt in het midden gebogen door druk uit te oefenen op twee steunen bij de matrijzeringang, het onderste deel van de blenk komt niet in contact met de matrijs. | Wanneer 2r≤L, F=0,7bt 2 Rm /(r+t) Als 2r>L, F=2bt 2 Rm /3L | F =KbtRm | F=0,4CKbtRm |
| Contactbuigen met dubbele hoek (U-vormige buigdelen) | 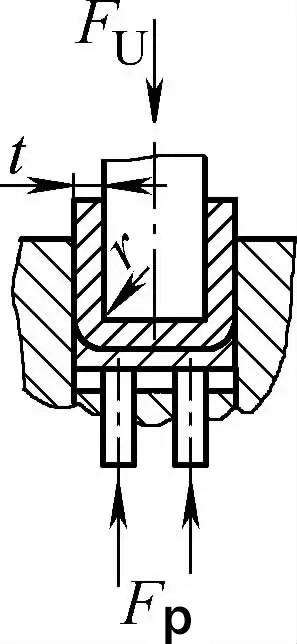 | Tijdens het buigen wordt een drukplaat gebruikt of een spleet die gelijk is aan of iets groter is dan t, maar er is geen effectcorrectiefunctie. | Als 2r≤L, Fu =0,7bt2Rm /(r+t)+Fp Als 2r>L, Fu =2bt2Rmn/3L+Fp | Fu =KbtRm +Fp | Fu=0,5CbtRm |
| Contact met dubbele hoek met impactcorrectie buigen (U-vormige buigdelen) | 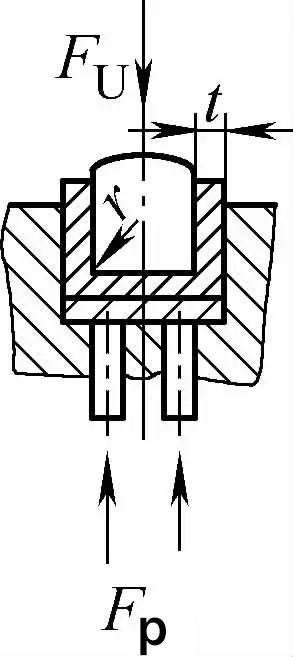 | Tijdens het buigen wordt een buigspleet kleiner dan of gelijk aan t gebruikt met een drukplaat (bovenplaat) en heeft ook de functie van botscorrectie | Fu=0,7bt2Rmn/L+Fp+qAb | Fu=1,3qAb | Fu=1,3qAb |
Opmerking: de symbolen in de tabel hebben de volgende betekenis:
- b - breedte van het buiggedeelte (mm);
- R - treksterkte van het materiaal van het buigdeel (MPa);
- L - lengte van het buigblenk op de steunpunten aan beide zijden van de opening van de buigmatrijs (mm);
- C - coëfficiënt, voor buigen met één hoek L>10t, C=1; voor buigen met twee hoeken r=t, C=1; n-aantal buighoeken (stukken);
- A - lageroppervlak van het buiggedeelte (mm²);
- F - vlakke correctiedruk (kN), over het algemeen 30%~100% van de buigkracht;
- K - materiaalsoortcoëfficiënt, de waarde staat in Tabel 2;
- q - eenheids(bots)correctiedruk (MPa), de waarde kan gevonden worden in Tabel 3.
Tabel 2 Materiaalsoort coëfficiënt K-waarde
| Materiaal | Verhouding L/t | |||||
| 3 | 10 | 15 | 20 | 25 | 30 | |
| 10 staal, 15 staal, messing, aluminium (zacht) | 0.23 | 0.18 | 0.12 | 0.09 | 0.073 | 0.060 |
| 20 staal, 25 staal, gehard aluminium | 0.21 | 0.17 | 0.11 | 0.08 | 0.070 | 0.057 |
| 20 staal, 25 staal, 40 staal, superhard aluminium | 0.20 | 0.16 | 0.10 | 0.08 | 0.065 | 0.053 |
Tabel 3 Benaderende waarde van de eenheids(bots)correctiedruk q tijdens buigen (eenheid: MPa)
| Materiaal | Buigmateriaal dikte t/mm | |
| ≤3 | >3~10 | |
| Aluminium | 30~40 | 50~60 |
| Messing | 60~80 | 80~100 |
| 10 staal, 15 staal, 20 staal | 80~100 | 100~120 |
| 25 staal, 30 staal, 35 staal | 100~120 | 120~150 |
Formules voor het berekenen van buigkracht
Tabel 4 Empirische formules voor het berekenen van buigkracht
| Buigmethode | Schema | Empirische formules | Opmerkingen |
| Vrij buigen | 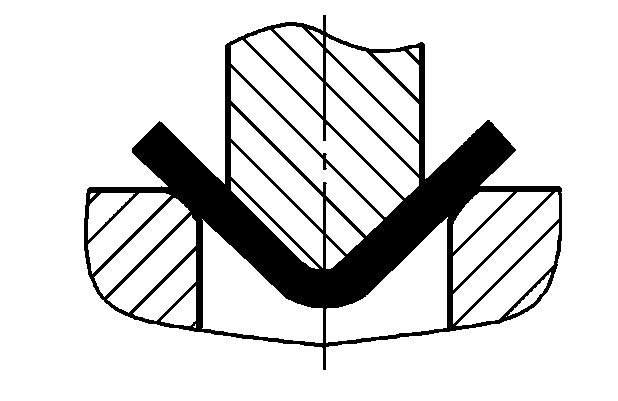 | P=(0,8Bt2σb)/(r+t) | waarbij P-Totale buigkracht (N) B-Breedte van het gebogen deel (mm) t-Materiaaldikte (mm) σb-Treksterkte (MPa) r-binnen buigradius (mm) A-Correctie deel projectie gebied (mm2 ) Eenheid correctiedruk (MPa), zie Tabel 5 voor de waarde |
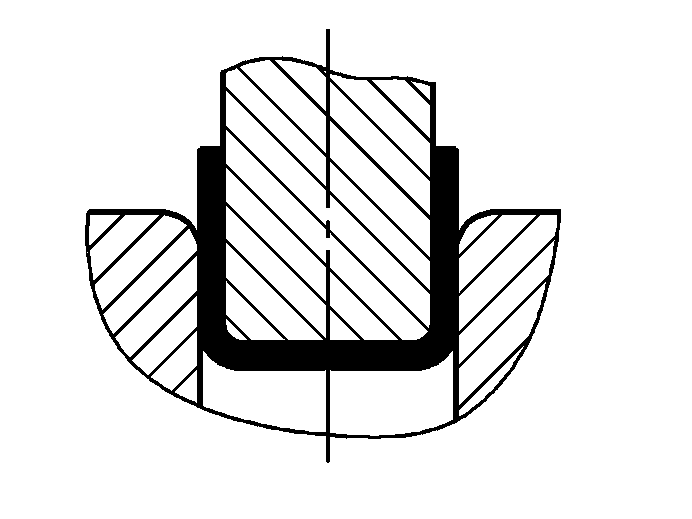 | P=(0,9Bt2σb)/(r+t) | ||
| Buigen met correctie | 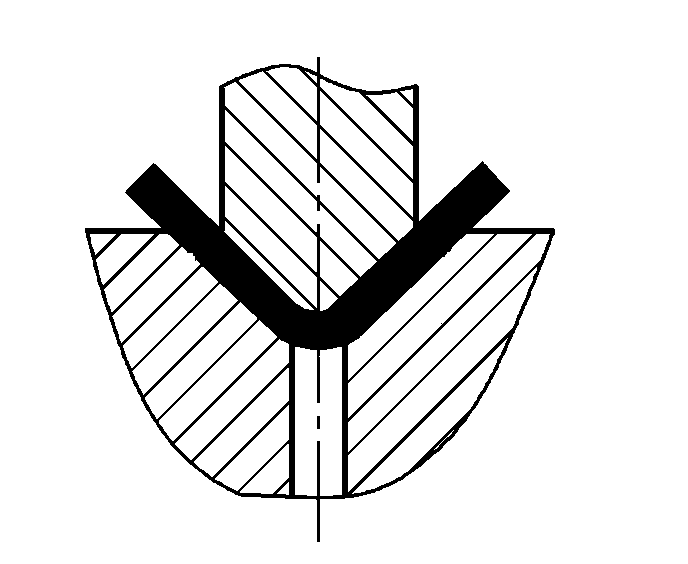 | P=(1,4Bt2σb)/(r+t) | |
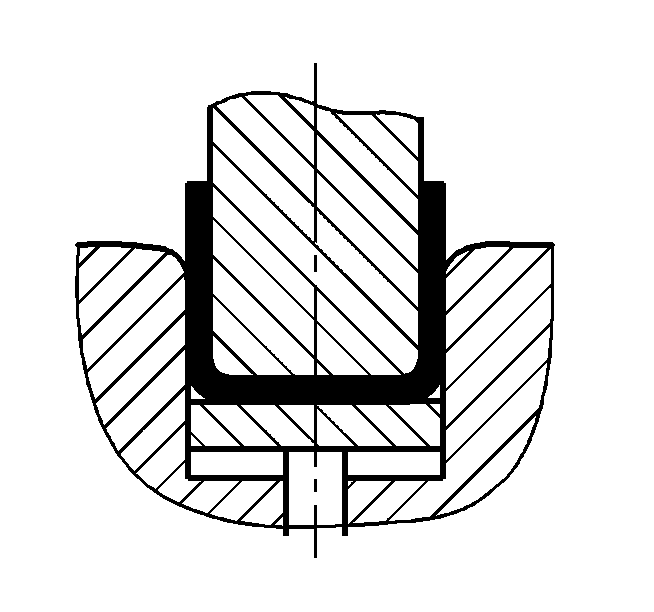 | P=(1,6Bt2σb)/(r+t) | ||
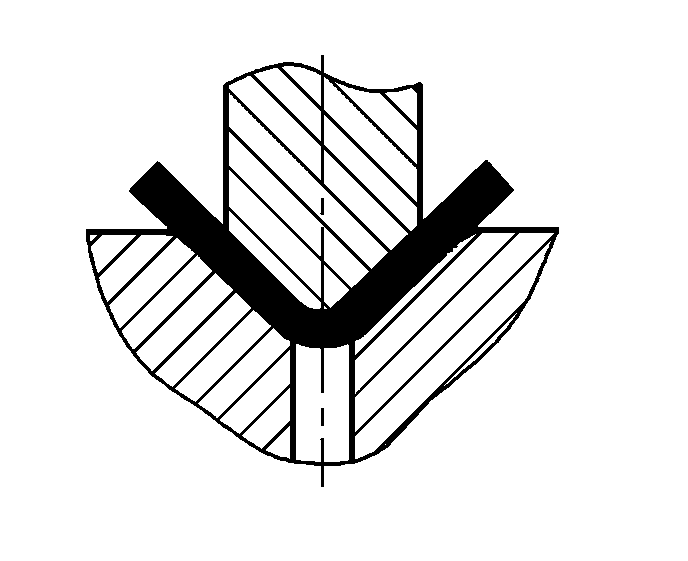 | P=(1,4Bt2σb)/(r+t)+Aq | ||
 | P=(1,6Bt2σb)/(r+t)+Aq |
Tabel 5 Eenheidscorrectiedruk q-waarde (eenheid: MPa)
| Materiaal | Materiaaldikte / mm | |||
| <1 | 1~3 | 3~6 | 6~10 | |
| Aluminium | 15~20 | 20~30 | 30~40 | 40~50 |
| Messing | 20~30 | 30~40 | 40~60 | 60~80 |
| 10~20 staal | 30~40 | 40~60 | 60~80 | 80~100 |
| 25~30 staal | 40~50 | 50~70 | 70~100 | 100~120 |
III. Berekening van buigarbeid
De buigarbeid van V-vormige buigonderdelen kan worden berekend met de volgende formule.
Wv=mFvh
Waar
- Wv - Buigarbeid van V-vormige buigonderdelen (J), over het algemeen berekend door contactopzettend buigen;
- m - correctiecoëfficiënt, m=0,32 voor V-vormige buigdelen, m=0,63 voor U-vormige buigdelen;
- Fv - Buigkracht van V-vormige buigdelen (kN), F v of F u Buigkracht kan de juiste berekeningsformule vinden in Tabel 1 om de buigkracht te berekenen.
- h - Diepte van de buigmatrijsholte (d.w.z. buigslag) (mm), h kan ook worden berekend met de volgende formule.
h=0,5L~0,4(t+r)
Waar
- L - Afstand tussen de twee steunpunten van de V-vormige buigdelen op de opening van de buigmatrijs (mm);
- t - Dikte van de buigdelen (mm);
- r - Buigstraal (mm).
IV. Vereenvoudigde grafische methode voor buigkracht en buigarbeid
Figuur 2 toont de grafische berekeningskolomgrafiek voor de buigkracht en buigarbeid van V-vormige en U-vormige buigonderdelen. Deze grafiek is handig in gebruik, de grafische berekening is snel en de resultaten komen dicht bij de werkelijkheid, geschikt voor gebruik op locatie.
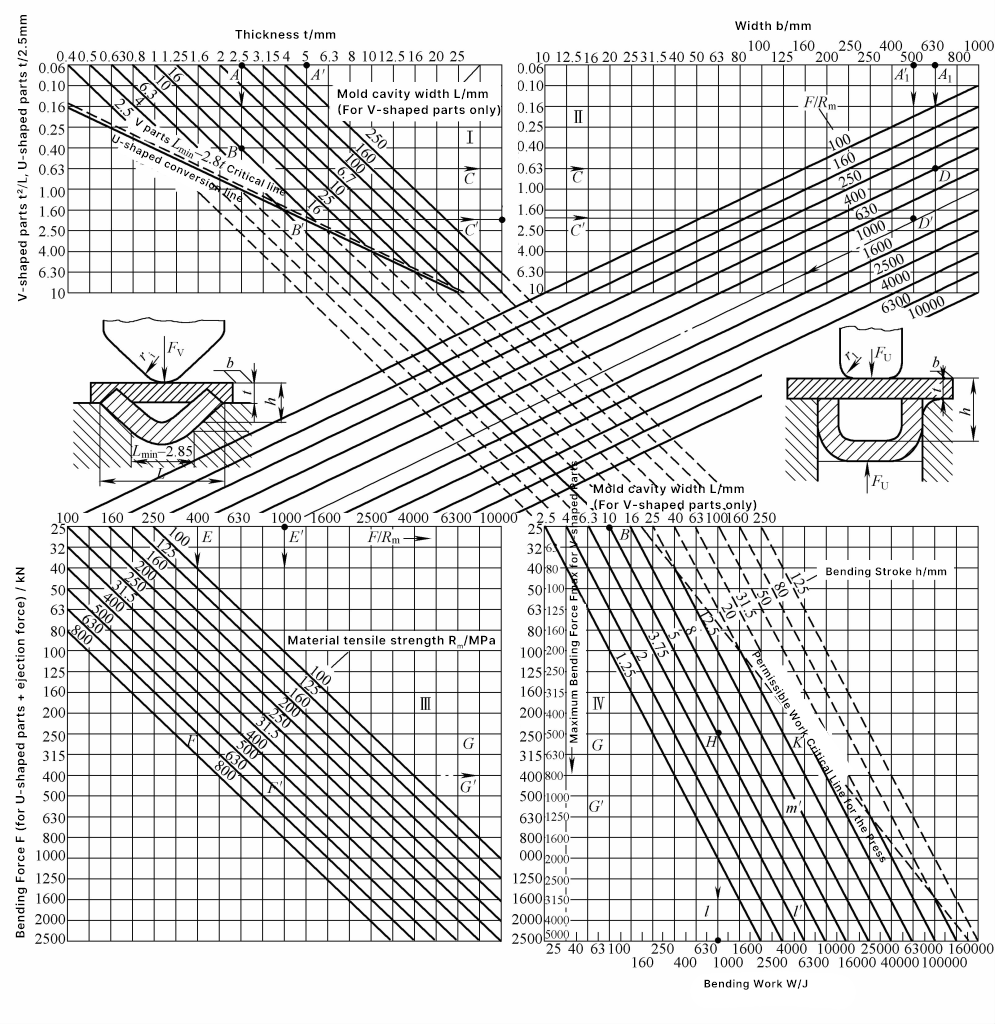
Opmerking: De symbolen in de grafiek betekenen het volgende:
- F - Buigkracht van V-vormige en U-vormige buigdelen (kN);
- W - Buigwerk van V-vormige en U-vormige buigdelen (J);
- H - Buigwerkslag van V-vormige en U-vormige buigdelen (mm);
- L, L min - Openingsbreedte van de buigmatrijs voor V-vormige buigonderdelen (mm), minimale openingsbreedte (mm);
- r - Binnenste buigradius van de buigonderdelen (mm);
- t - Dikte van de buigdelen (mm).
Grafisch rekenvoorbeeld. Gegeven is een V-vormig buigdeel met t=2,5mm, openingsbreedte van de buigmatrijs L=10mm. In gebied I van figuur 2 is t2/L=0,63 (zie ABC-lijn). Gegeven de breedte van het buigdeel b=630mm, treksterkte van het materiaal R m =630MPa, in gebieden II en III, vind de A1 DEF lijn, en in gebied III, langs de rechter verlenglijn, de FG lijn, resulterend in een buigkracht Fv =250kN.
In gebied IV, rekening houdend met de nivelleringsrichtdruk, is de totale druk F∑ =2F=500kN. De buigbeweging h=0,5L=5mm, correctiecoëfficiënt m=0,32, dus de buigarbeid Wv =mF∑ h=800J, zoals weergegeven in de BH-lijn en CHI-lijn in figuur 2.