Siła gięcia jest ważną podstawą projektowania procesów tłoczenia, wyboru pras i projektowania form.
Ponieważ wielkość siły gnącej jest związana nie tylko z rozmiarem półfabrykatu, właściwościami mechanicznymi materiału, odległością między podporami matrycy, promieniem gięcia i prześwitem między formami, ale także w dużym stopniu związana z metodą gięcia, trudno jest wykonać dokładne obliczenia przy użyciu metod analizy teoretycznej. Dlatego też, w produkcji, empiryczne wzory wymienione w tabeli 1 są zwykle używane do zgrubnego obliczenia siły zginającej.
I. Teoretyczne podstawy i metody obliczeń siły zginającej
Teoretyczna metoda obliczania siły zginającej jest wyprowadzana w warunkach równowagi statycznej, w których suma różnych sił zewnętrznych działających na zginany półfabrykat wynosi zero, a zewnętrzny moment obrotowy działający na zginany półfabrykat jest równy jego wewnętrznemu momentowi oporowemu, poprzez konwencjonalne obliczenia.
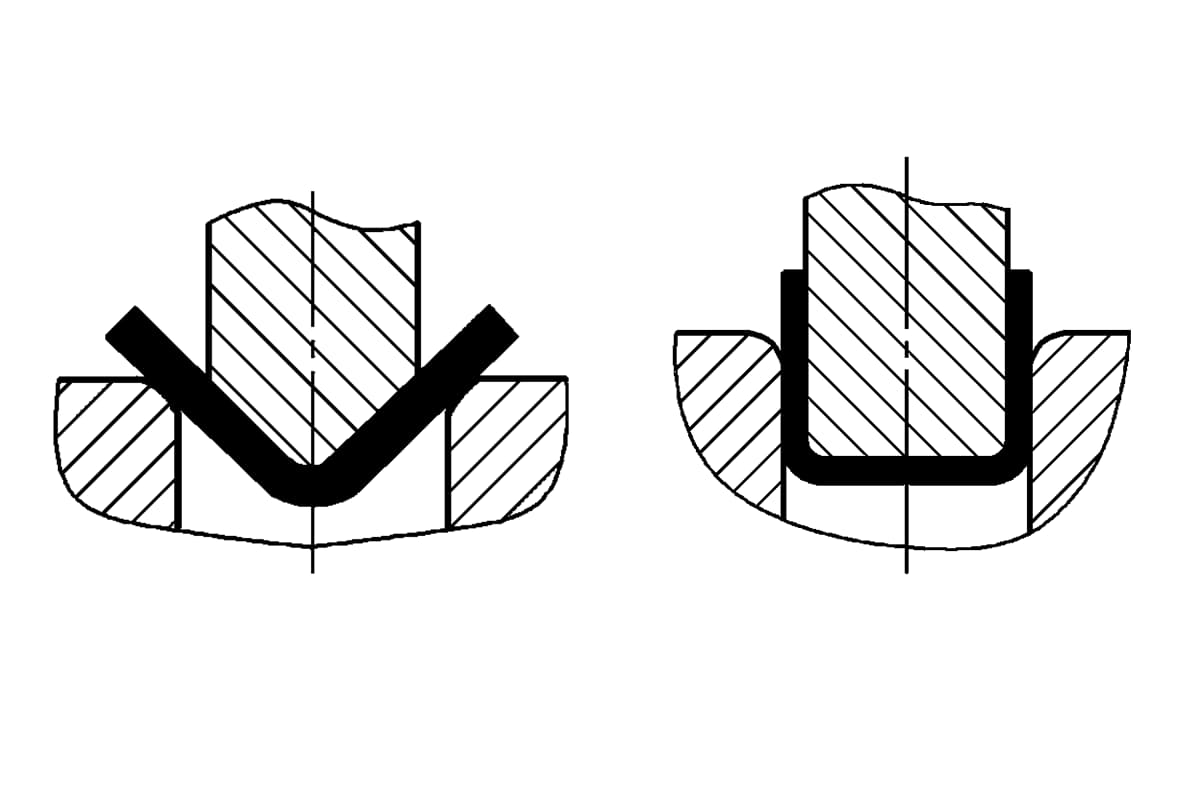
Metoda gięcia i struktura matrycy zmieniają stan naprężenia giętego półfabrykatu. Różne metody gięcia skutkują bardzo różnymi ciśnieniami gięcia. Biorąc pod uwagę powszechnie stosowane metody w kształcie litery V i U części do gięcia Jako przykłady, jak pokazano na rysunku 1, można je formować przez gięcie za pomocą zwykłych matryc do gięcia pełnej stali, odpowiednio przy użyciu gięcia swobodnego, gięcia kontaktowego i gięcia z korekcją uderzenia.
- a) Części gnące w kształcie litery V
- b) Części gnące w kształcie litery U
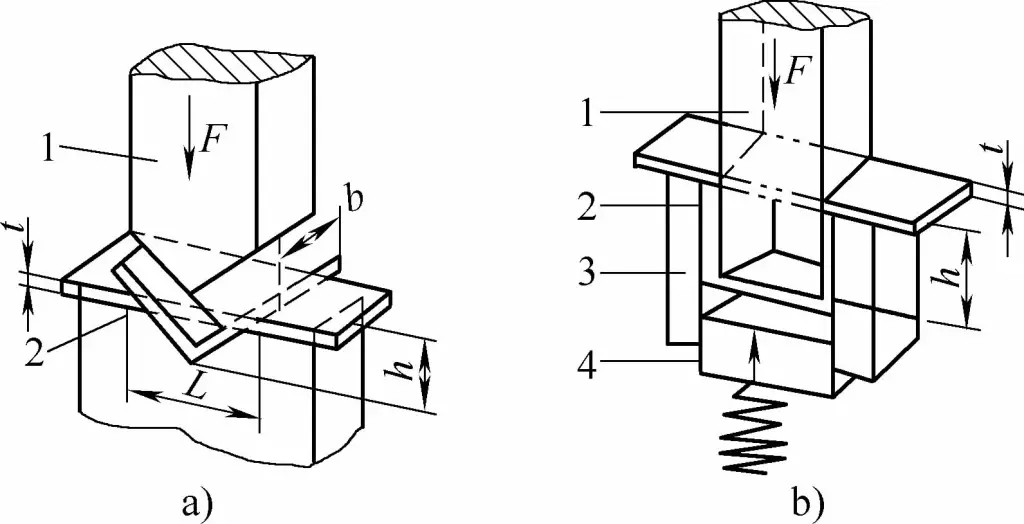
- 1 - Stempel do gięcia
- 2 - Część gnąca
- 3 - Matryca do gięcia w kształcie litery U
- 4 - Górne narzędzie
- L - Szerokość otworu matrycy w kształcie litery U
- t - Grubość części giętej
- h - Głębokość wnęki matrycy gnącej w kształcie litery V
Części gnące w kształcie litery V wykorzystują skoncentrowane obciążenie w środku dwóch podpór płaskiego półfabrykatu do czystego gięcia i swobodnego gięcia, głównie na placach budowy. Online, małe i średnie części do gięcia blach są najczęściej formowane przez gięcie spęczania kontaktowego, a części do gięcia płyt o wysokiej wytrzymałości i średniej grubości są często gięte na prasach ciernych przy użyciu gięcia korekcji uderzenia. Gięcie swobodne wymaga mniejszego nacisku, bez dodatkowego nacisku, tylko zwykłej siły gięcia.
II. Obliczanie siły zginającej za pomocą różnych metod zginania
Wzory obliczeniowe siły zginającej dla różnych metod zginania przedstawiono w tabeli 1.
Tabela 1 Wzory obliczeniowe siły zginającej dla różnych metod zginania
| Nazwa | Schemat | Charakterystyka odkształcenia przy zginaniu | Wzór obliczania siły zginającej | ||
| Teoretyczne | W przybliżeniu | Zalecane | |||
| Gięcie swobodne pod jednym kątem (część gnąca w kształcie litery V) | 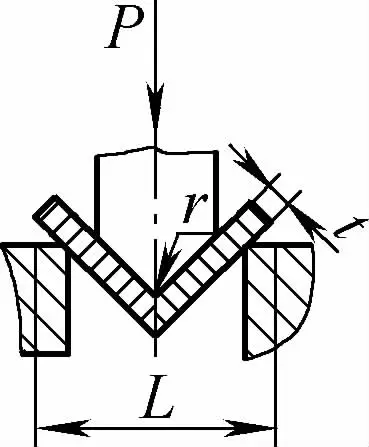 | Półfabrykat jest zginany w środku poprzez wywieranie nacisku na dwa wsporniki przy wejściu do matrycy, dolna część nie styka się z formą. | Gdy 2r≤L, F=0,7bt3 Rm /(r+t) Gdy 2r>L, F=2bt2 Rm /3L | F = KbtRm | F=Cbt2Rm/L |
| Gięcie stykowe pod jednym kątem (części gnące w kształcie litery V) | 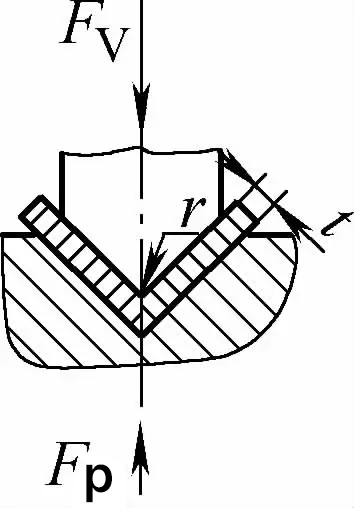 | Przed zakończeniem procesu gięcia, półfabrykat do gięcia jest w bliskim kontakcie z całą wnęką formy. Płyta dociskowa jest zwykle używana do wykonania gięcia szczelina matrycy większa lub równa t | Gdy 2r≤L, Fv =0,7bt2 Rm /(r+t)+Fp Gdy 2r>L, Fv =2bt2 Rm /3L+Fp | Fv=KbtRm +Fp | Fv=2Cbt2Rm/L |
| Styk pod jednym kątem z gięciem korygującym uderzenie (części gnące w kształcie litery V) | 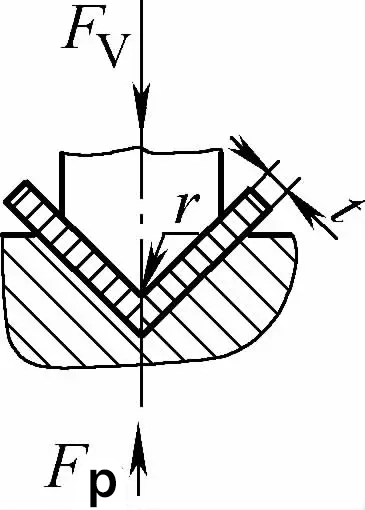 | W oparciu o zginanie kontaktowe, ma również funkcję korekcji uderzenia. Szczelina matrycy gnącej jest zazwyczaj mniejsza lub równa t | Fv=0,7bt2Rm/L+Fp+qAb | Fv=1,3qAb | Fv=1,39qAb |
| Swobodne gięcie pod podwójnym kątem (Części gnące w kształcie litery U) | 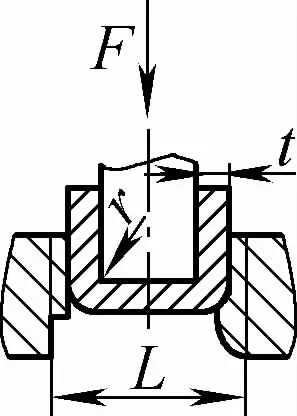 | Półfabrykat do gięcia jest wyginany w środku poprzez wywieranie nacisku na dwa wsporniki przy wejściu do matrycy, dolna część półfabrykatu nie styka się z formą. | Gdy 2r≤L, F=0,7bt 2 Rm /(r+t) Gdy 2r>L, F=2bt 2 Rm /3L | F =KbtRm | F=0.4CKbtRm |
| Gięcie stykowe pod podwójnym kątem (części gnące w kształcie litery U) | 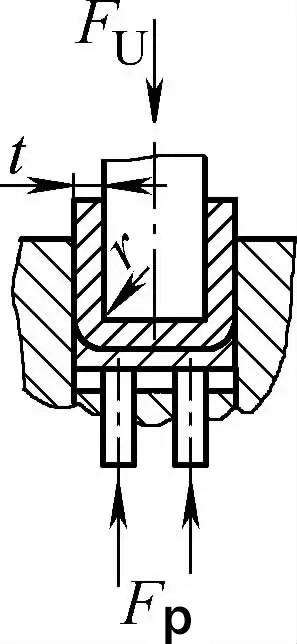 | Podczas gięcia używana jest płyta dociskowa lub szczelina równa lub nieco większa niż t, ale nie ma funkcji korekcji uderzenia | Gdy 2r≤L, Fu =0,7bt2Rm /(r+t)+Fp Gdy 2r>L, Fu =2bt2Rmn/3L+Fp | Fu =KbtRm +Fp | Fu=0,5CbtRm |
| Styk dwukątowy z gięciem korygującym uderzenie (części gnące w kształcie litery U) | 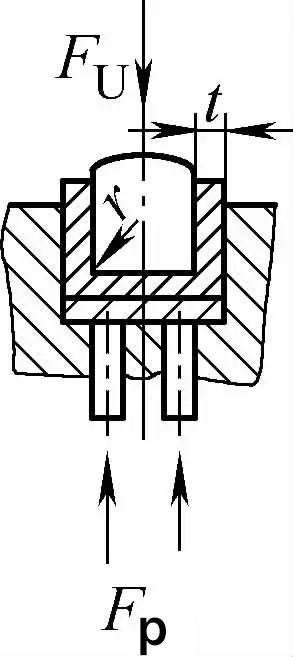 | Podczas gięcia, szczelina gięcia mniejsza lub równa t jest używana z płytą dociskową (płyta górna) i ma również funkcję korekcji uderzenia | Fu=0,7bt2Rmn/L+Fp+qAb | Fu=1,3qAb | Fu=1,3qAb |
Uwaga: Znaczenie symboli w tabeli jest następujące:
- b - szerokość części zginanej (mm);
- R - wytrzymałość na rozciąganie materiału części zginanej (MPa);
- L - długość wykroju gnącego w punktach podparcia po obu stronach otworu matrycy gnącej (mm);
- C - współczynnik, dla zginania pod jednym kątem L>10t, C=1; dla zginania pod dwoma kątami r=t, C=1; n - liczba kątów zginania (sztuk);
- A - powierzchnia nośna części zginanej (mm²);
- F - płaski nacisk korekcyjny (kN), zazwyczaj 30%~100% siły zginającej;
- K - współczynnik typu materiału, wartość można znaleźć w tabeli 2;
- q - jednostkowe (udarowe) ciśnienie korekcyjne (MPa), wartość można znaleźć w tabeli 3.
Tabela 2 Współczynnik typu materiału Wartość K
| Materiał | Stosunek L/t | |||||
| 3 | 10 | 15 | 20 | 25 | 30 | |
| 10 stal, 15 stal, mosiądz, aluminium (miękkie) | 0.23 | 0.18 | 0.12 | 0.09 | 0.073 | 0.060 |
| 20 stal, 25 stal, hartowane aluminium | 0.21 | 0.17 | 0.11 | 0.08 | 0.070 | 0.057 |
| 20 stal, 25 stal, 40 stal, super twarde aluminium | 0.20 | 0.16 | 0.10 | 0.08 | 0.065 | 0.053 |
Tabela 3 Przybliżona wartość jednostkowego (udarowego) ciśnienia korekcyjnego q podczas zginania (jednostka: MPa)
| Materiał | Grubość giętego materiału t/mm | |
| ≤3 | >3~10 | |
| Aluminium | 30~40 | 50~60 |
| Mosiądz | 60~80 | 80~100 |
| 10 stal, 15 stal, 20 stal | 80~100 | 100~120 |
| 25 stal, 30 stal, 35 stal | 100~120 | 120~150 |
Wzory do obliczania siły zginającej
Tabela 4 Wzory empiryczne do obliczania siły zginającej
| Metoda gięcia | Schemat | Wzory empiryczne | Uwagi |
| Swobodne gięcie | 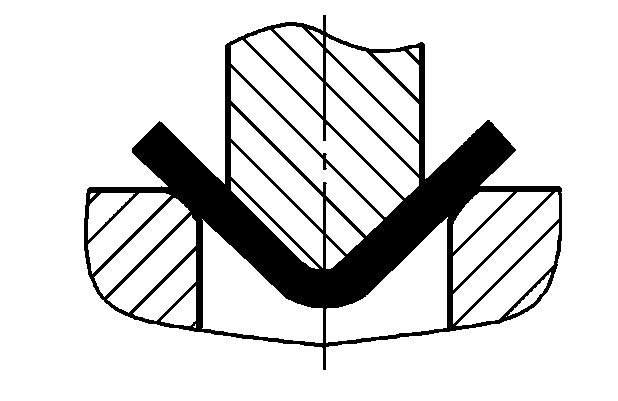 | P=(0.8Bt2σb)/(r+t) | gdzie P - Całkowita siła zginająca (N) B-Szerokość wygiętej części (mm) t-Grubość materiału (mm) σb-Wytrzymałość na rozciąganie (MPa) r-Wewnętrzny promień gięcia (mm) Obszar projekcji części korekcyjnej A (mm)2 ) Jednostkowe ciśnienie korekcyjne (MPa), patrz Tabela 5 dla jego wartości |
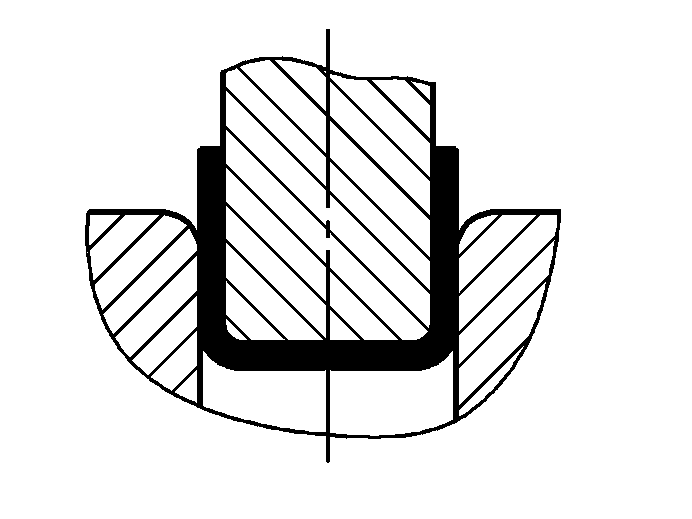 | P=(0.9Bt2σb)/(r+t) | ||
| Gięcie z korektą | 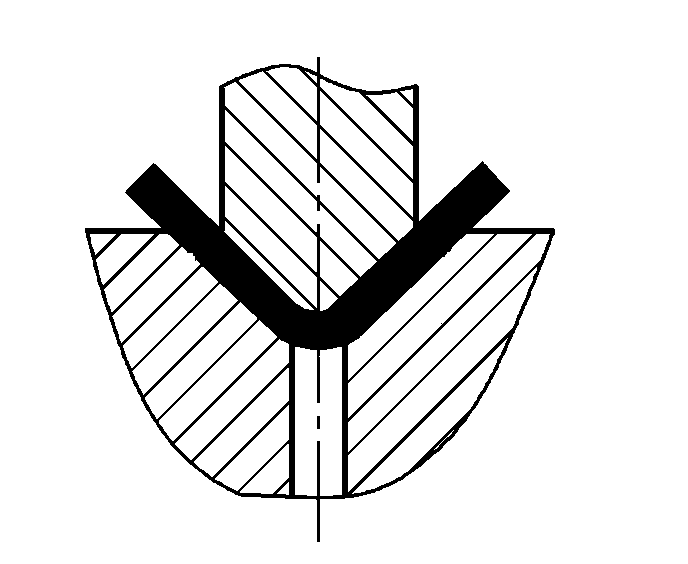 | P=(1.4Bt2σb)/(r+t) | |
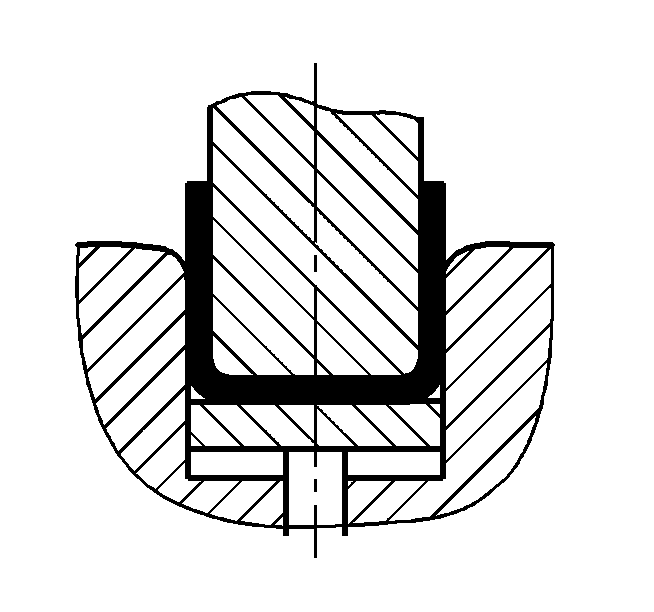 | P=(1.6Bt2σb)/(r+t) | ||
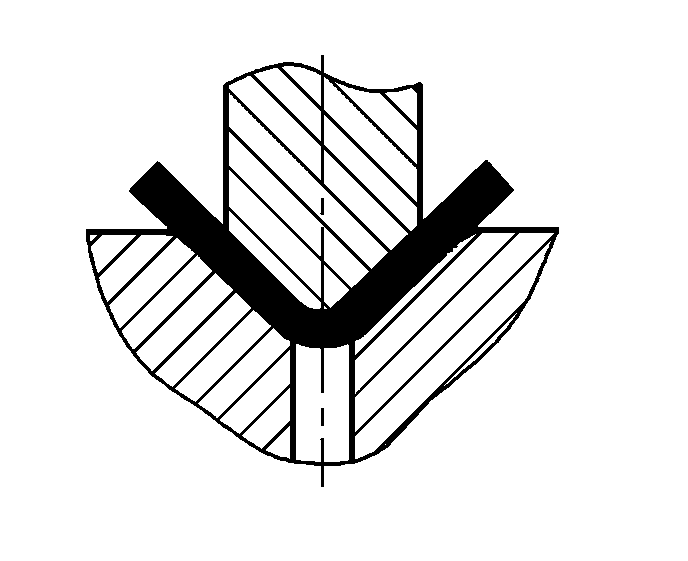 | P=(1.4Bt2σb)/(r+t)+Aq | ||
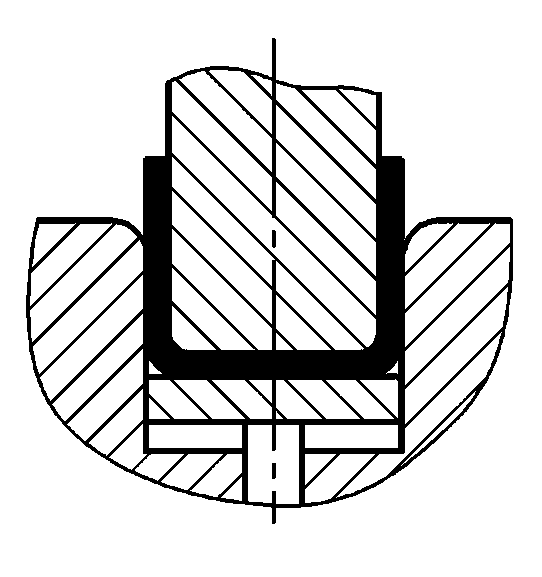 | P=(1.6Bt2σb)/(r+t)+Aq |
Tabela 5 Wartość q jednostkowego ciśnienia korekcyjnego (jednostka: MPa)
| Materiał | Grubość materiału / mm | |||
| <1 | 1~3 | 3~6 | 6~10 | |
| Aluminium | 15~20 | 20~30 | 30~40 | 40~50 |
| Mosiądz | 20~30 | 30~40 | 40~60 | 60~80 |
| 10~20 stal | 30~40 | 40~60 | 60~80 | 80~100 |
| 25~30 stali | 40~50 | 50~70 | 70~100 | 100~120 |
III. Obliczanie pracy zginania
Pracę gięcia elementów gnących w kształcie litery V można obliczyć za pomocą następującego wzoru.
Wv=mFvh
Gdzie
- Wv - Praca gięcia części gnących w kształcie litery V (J), zwykle obliczana na podstawie gięcia spęczania kontaktowego;
- m - Współczynnik korekcji, m=0,32 dla części giętych w kształcie litery V, m=0,63 dla części giętych w kształcie litery U;
- Fv - Siła zginająca części giętych w kształcie litery V (kN), F v lub F u Aby obliczyć siłę zginającą, można znaleźć odpowiedni wzór obliczeniowy w tabeli 1.
- h - Głębokość wgłębienia matrycy gnącej (tj. skok gięcia) (mm), h można również obliczyć za pomocą następującego wzoru.
h=0.5L~0.4(t+r)
Gdzie
- L - Odległość między dwoma punktami podparcia części gnących w kształcie litery V na otworze matrycy gnącej (mm);
- t - Grubość elementów gnących (mm);
- r - promień gięcia (mm).
IV. Uproszczona metoda graficzna dla siły zginającej i pracy zginania
Rysunek 2 przedstawia graficzny wykres kolumny obliczeniowej dla siły zginającej i pracy zginania części giętych w kształcie litery V i U. Wykres ten jest wygodny w użyciu, obliczenia graficzne są szybkie, a wyniki są zbliżone do rzeczywistości, odpowiednie do użytku na miejscu.
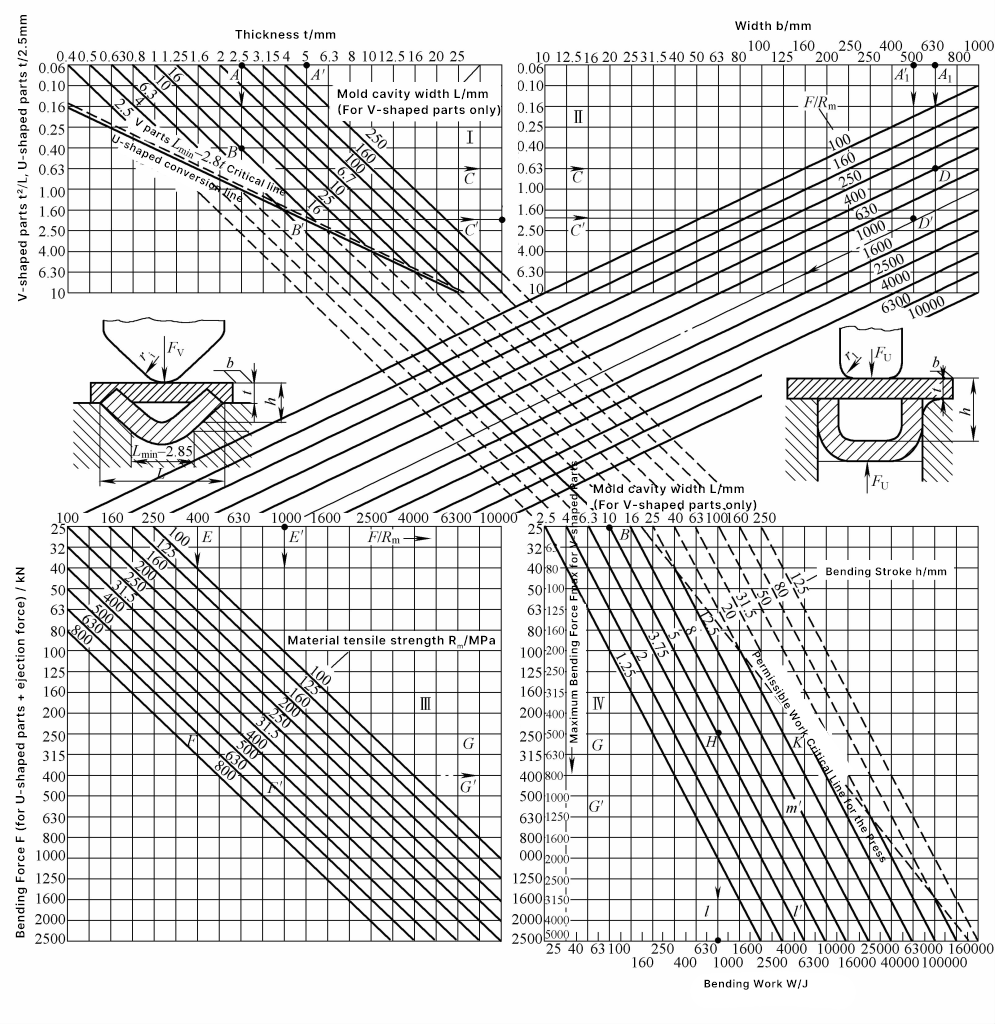
Uwaga: Symbole na wykresie oznaczają, co następuje:
- F - Siła zginająca części zginanych w kształcie litery V i U (kN);
- W - Praca gięcia części giętych w kształcie litery V i U (J);
- H - Skok roboczy gięcia elementów gnących w kształcie litery V i U (mm);
- L, L min - Szerokość otwarcia matrycy gnącej dla elementów gnących w kształcie litery V (mm), minimalna szerokość otwarcia (mm);
- r - Wewnętrzny promień gięcia części gnących (mm);
- t - Grubość elementów gnących (mm).
Przykład obliczeń graficznych. Biorąc pod uwagę część gnącą w kształcie litery V z t=2,5 mm, szerokość otworu matrycy gnącej L=10 mm. W obszarze I na rysunku 2, t2/L=0,63 (patrz linia ABC). Biorąc pod uwagę szerokość zginanej części b=630mm, wytrzymałość na rozciąganie materiału R m =630MPa, w obszarach II i III znaleźć A1 DEF, a w obszarze III, wzdłuż prawej linii przedłużającej, znaleźć linię FG, co skutkuje siłą zginającą Fv =250kN.
W obszarze IV, biorąc pod uwagę ciśnienie prostujące, całkowite ciśnienie wynosi F∑ =2F=500kN. Skok roboczy gięcia h=0,5L=5mm, współczynnik korekcji m=0,32, a zatem praca gięcia Wv =mF∑ h=800J, jak pokazano na liniach BH i CHI na rysunku 2.