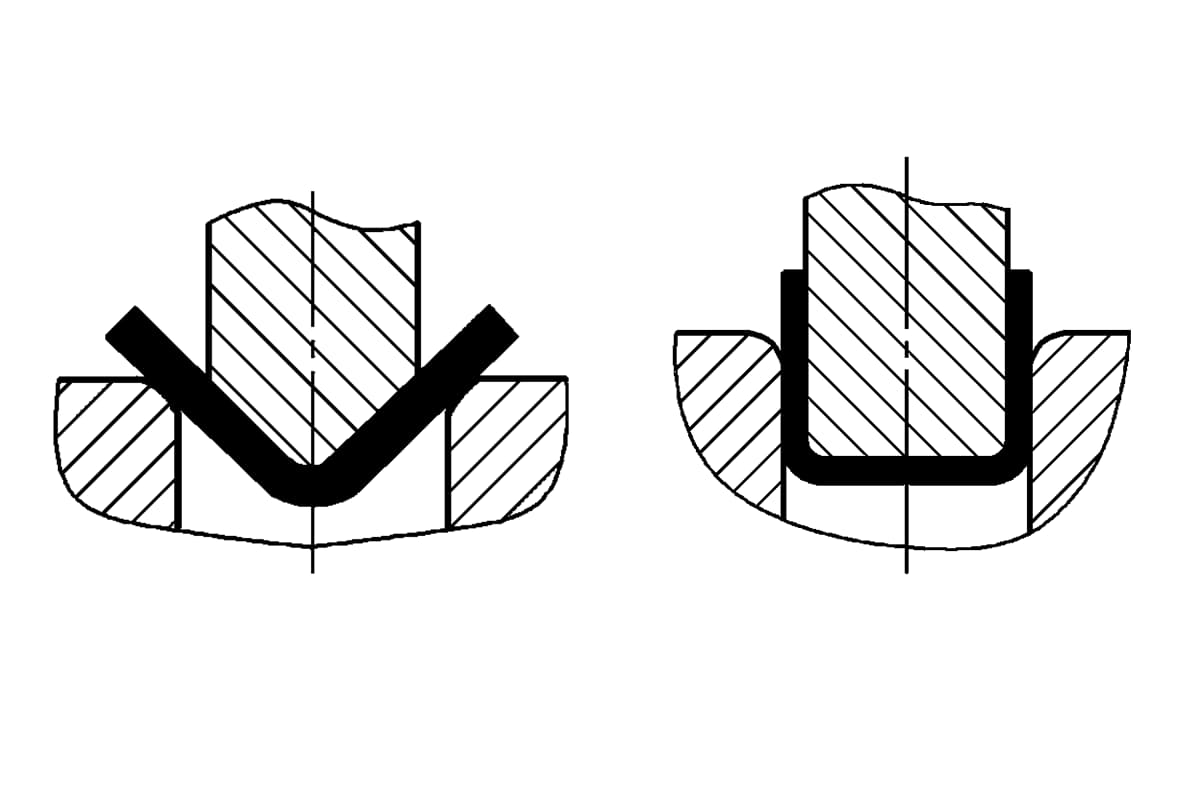
A força de flexão é uma base importante para projetar processos de estampagem, selecionar prensas e projetar moldes.
Como a magnitude da força de flexão está relacionada não apenas ao tamanho do blank, às propriedades mecânicas do material, à distância entre os suportes da matriz, ao raio de flexão e à folga entre os moldes, mas também está muito relacionada ao método de flexão, é difícil fazer cálculos precisos usando métodos de análise teórica. Portanto, na produção, as fórmulas empíricas listadas na Tabela 1 são normalmente usadas para um cálculo aproximado da força de flexão.
I. Base de cálculo teórico e métodos para força de flexão
O método de cálculo teórico da força de flexão é derivado sob as condições de equilíbrio estático, em que a soma de várias forças externas que atuam no bloco de flexão é zero e o torque externo que atua no bloco de flexão é igual ao seu torque de resistência interna, por meio de cálculo convencional.
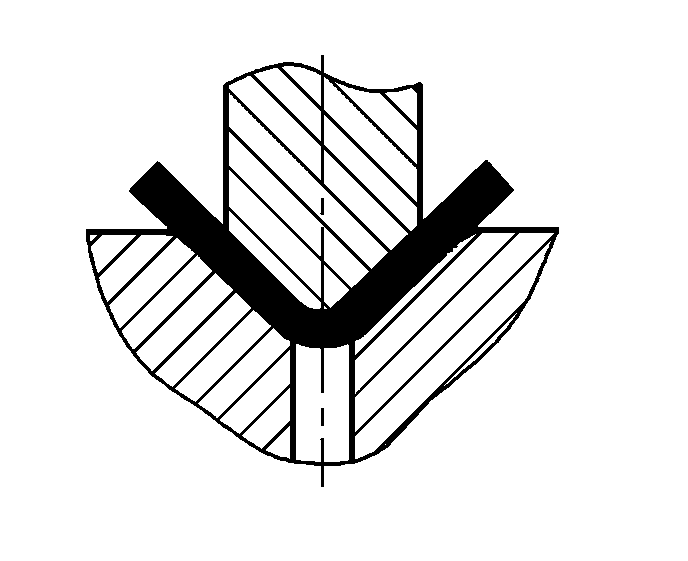
O método de dobra e a estrutura da matriz alterarão o estado de tensão do blank de dobra. Diferentes métodos de dobra resultam em pressões de dobra muito diferentes. Tomando os métodos comumente usados em forma de V e em forma de U peças de dobra como exemplos, conforme mostrado na Figura 1, eles podem ser formados por flexão com matrizes de flexão de aço comum, respectivamente usando flexão livre, flexão por contato e flexão por correção de impacto.
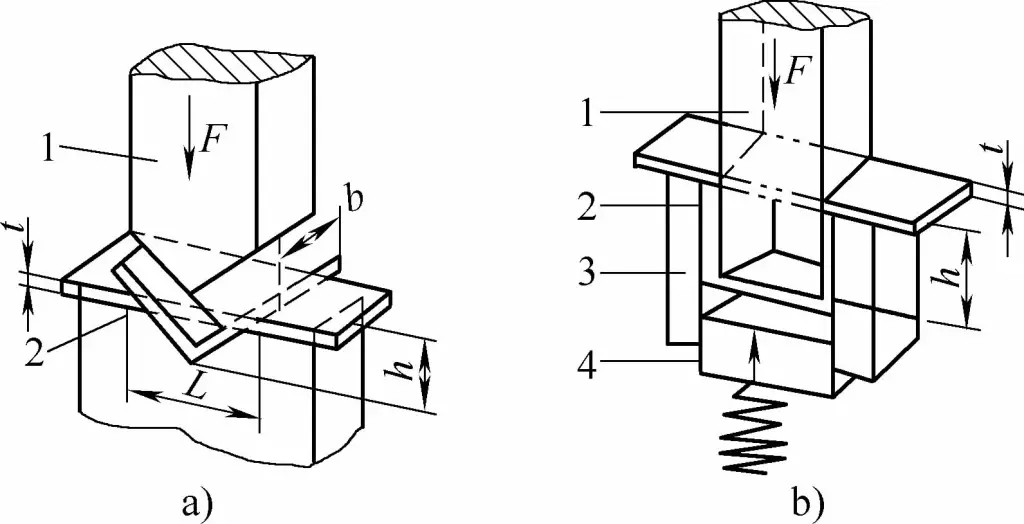
- a) Peças de dobra em forma de V
- b) Peças de dobra em forma de U
- 1 - Punção de dobra
- 2 - Peça de dobra
- 3 - Matriz de dobragem em forma de U
- 4 - Ferramenta superior
- L - Largura da abertura da matriz em forma de U
- t - Espessura da peça de flexão
- h - Profundidade da cavidade da matriz de dobra em forma de V
As peças de dobra em forma de V usam uma carga concentrada no meio de dois suportes de uma peça plana em branco para dobra pura e dobra livre, usadas principalmente em canteiros de obras. As peças de dobra de chapas metálicas on-line, de pequeno e médio porte, são formadas principalmente por dobra por contato, e as peças de dobra de chapas de espessura média e alta resistência são frequentemente dobradas em prensas de fricção usando dobra por correção de impacto. A dobra livre requer menos pressão, sem pressão adicional, apenas com força de dobra simples.
II. Cálculo da força de flexão por meio de vários métodos de flexão
As fórmulas de cálculo da força de flexão por vários métodos de flexão são mostradas na Tabela 1.
Tabela 1 Fórmulas de cálculo para força de flexão por vários métodos de flexão
| Nome | Esquema | Características da deformação por flexão | Fórmula de cálculo da força de flexão | ||
| Teórico | Aproximado | Recomendado | |||
| Flexão livre de ângulo único (parte dobrada em forma de V) | 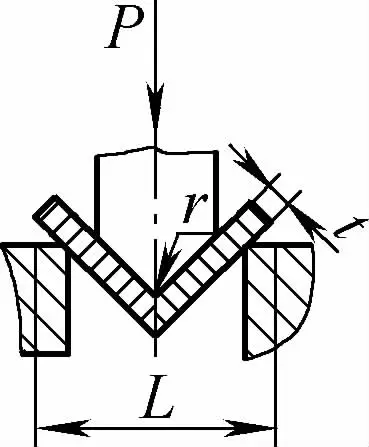 | A peça bruta é dobrada no meio, aplicando pressão em dois suportes na entrada da matriz; a parte inferior não entra em contato com o molde | Quando 2r≤L, F=0,7bt3 Rm /(r+t) Quando 2r>L, F=2bt2 Rm /3L | F = KbtRm | F=Cbt2Rm/L |
| Flexão de contato de ângulo único (Peças de dobra em forma de V) | 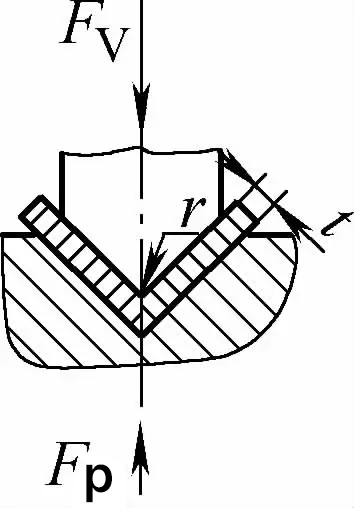 | Antes da conclusão do processo de dobra, a placa de dobra está em contato próximo com toda a cavidade do molde. Geralmente, uma placa de pressão é usada para fazer a dobra lacuna da matriz maior ou igual a t | Quando 2r≤L, Fv =0,7bt2 Rm /(r+t)+Fp Quando 2r>L, Fv =2bt2 Rm /3L+Fp | Fv=KbtRm +Fp | Fv=2Cbt2Rm/L |
| Contato de ângulo único com flexão de correção de impacto (peças de flexão em forma de V) | 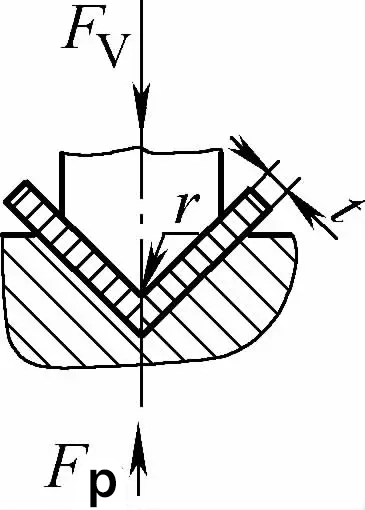 | Com base na dobra por contato, ela também tem a função de correção de impacto. A lacuna da matriz de flexão é geralmente menor ou igual a t | Fv=0,7bt2Rm/L+Fp+qAb | Fv=1,3qAb | Fv=1,39qAb |
| Flexão livre de ângulo duplo (Peças de dobra em forma de U) | 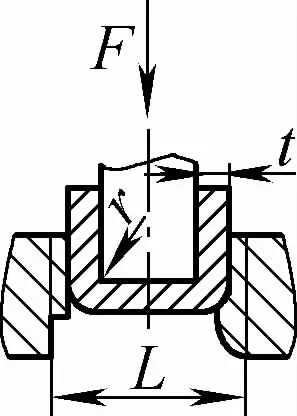 | O blank de dobra é dobrado no meio, aplicando pressão em dois suportes na entrada da matriz; a parte inferior do blank não entra em contato com o molde | Quando 2r≤L, F=0,7bt 2 Rm /(r+t) Quando 2r>L, F=2bt 2 Rm /3L | F =KbtRm | F=0,4CKbtRm |
| Dobra de contato de ângulo duplo (peças de dobra em forma de U) | 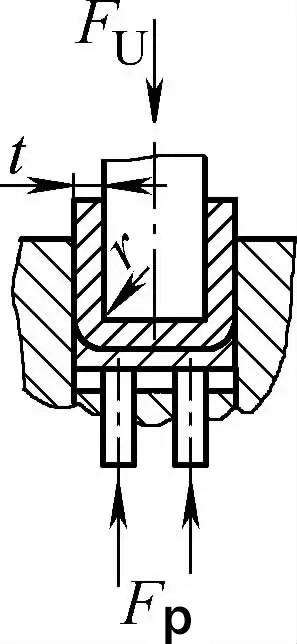 | Durante a flexão, uma placa de pressão é usada ou uma folga igual ou ligeiramente maior que t é usada, mas não há função de correção de impacto | Quando 2r≤L, Fu =0,7bt2Rm /(r+t)+Fp Quando 2r>L, Fu =2bt2Rmn/3L+Fp | Fu =KbtRm +Fp | Fu=0,5CbtRm |
| Contato de ângulo duplo com dobra de correção de impacto (peças de dobra em forma de U) | 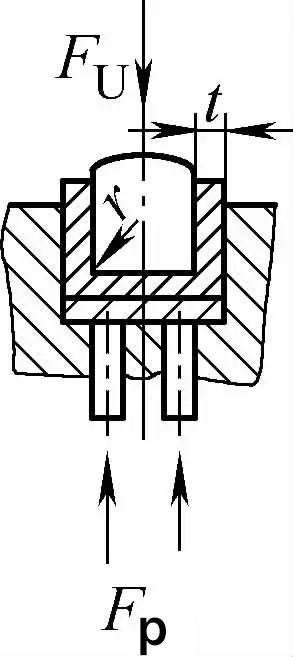 | Durante a flexão, uma folga de flexão menor ou igual a t é usada com uma placa de pressão (placa superior) e também tem a função de correção de impacto | Fu=0,7bt2Rmn/L+Fp+qAb | Fu=1,3qAb | Fu=1,3qAb |
Observação: Os significados dos símbolos na tabela são os seguintes:
- b - largura da peça de flexão (mm);
- R - resistência à tração do material da peça de flexão (MPa);
- L - comprimento do blank de dobra nos pontos de apoio em ambos os lados da abertura da matriz de dobra (mm);
- C - coeficiente, para flexão de ângulo único L>10t, C=1; para flexão de ângulo duplo r=t, C=1; n-número de ângulos de flexão (peças);
- A - área de rolamento da peça dobrada (mm²);
- F - pressão de correção plana (kN), geralmente 30%~100% da força de flexão;
- K - coeficiente do tipo de material, o valor pode ser encontrado na Tabela 2;
- q - pressão de correção da unidade (impacto) (MPa), o valor pode ser encontrado na Tabela 3.
Tabela 2 Valor K do coeficiente do tipo de material
| Material | Proporção L/t | |||||
| 3 | 10 | 15 | 20 | 25 | 30 | |
| 10 aço, 15 aço, latão, alumínio (macio) | 0.23 | 0.18 | 0.12 | 0.09 | 0.073 | 0.060 |
| 20 aço, 25 aço, alumínio endurecido | 0.21 | 0.17 | 0.11 | 0.08 | 0.070 | 0.057 |
| Aço 20, aço 25, aço 40, alumínio superduro | 0.20 | 0.16 | 0.10 | 0.08 | 0.065 | 0.053 |
Tabela 3 Valor aproximado da pressão de correção da unidade (impacto) q durante a flexão (unidade: MPa)
| Material | Espessura do material de dobra t/mm | |
| ≤3 | >3~10 | |
| Alumínio | 30~40 | 50~60 |
| Latão | 60~80 | 80~100 |
| 10 aço, 15 aço, 20 aço | 80~100 | 100~120 |
| 25 aço, 30 aço, 35 aço | 100~120 | 120~150 |
Fórmulas para calcular a força de flexão
Tabela 4 Fórmulas empíricas para calcular a força de flexão
| Método de flexão | Esquema | Fórmulas empíricas | Notas |
| Flexão livre | 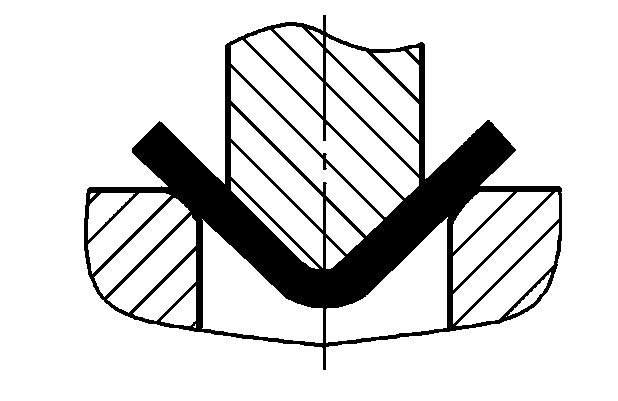 | P=(0,8Bt2σb)/(r+t) | onde P - Força total de flexão (N) B-Largura da peça dobrada (mm) t-Espessura do material (mm) σb-Resistência à tração (MPa) r-Interior raio de curvatura (mm) Área de projeção da peça de correção A (mm)2 ) Pressão de correção da unidade (MPa), consulte a Tabela 5 para obter seu valor |
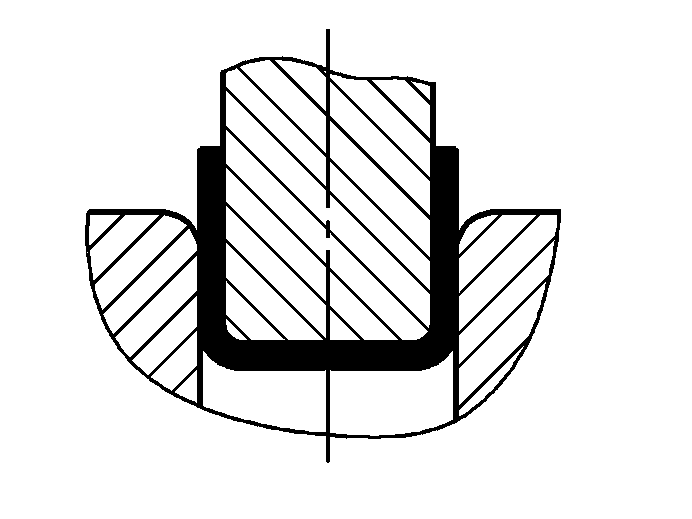 | P=(0,9Bt2σb)/(r+t) | ||
| Flexão com correção | 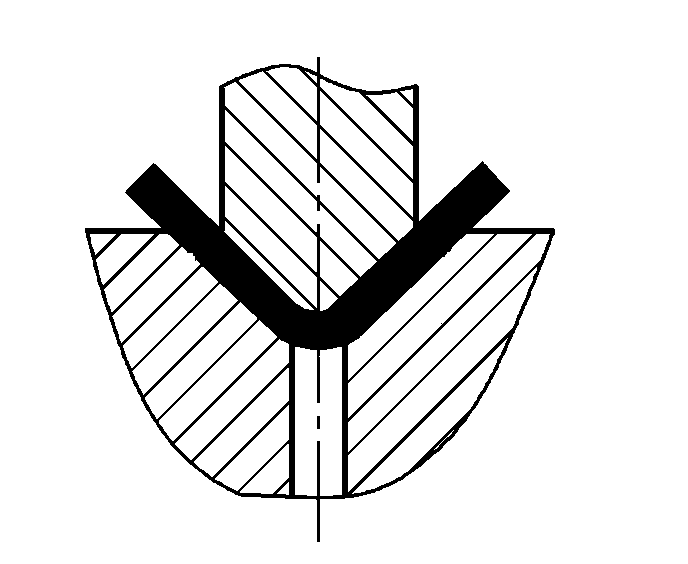 | P=(1,4Bt2σb)/(r+t) | |
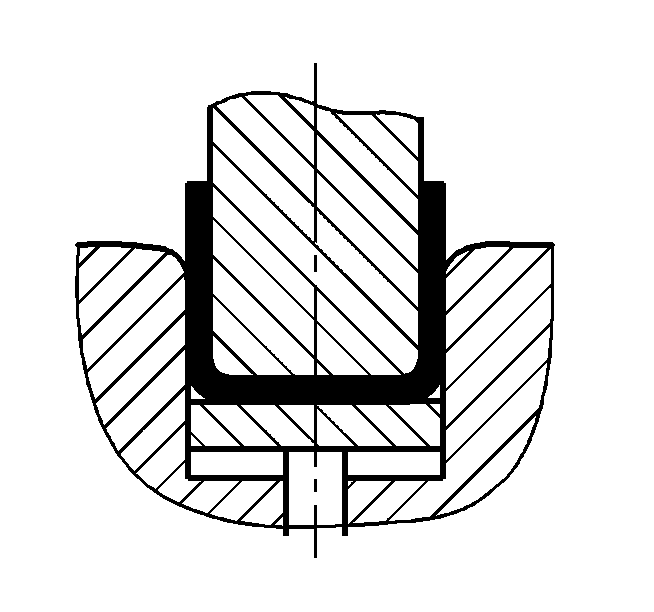 | P=(1,6Bt2σb)/(r+t) | ||
 | P=(1,4Bt2σb)/(r+t)+Aq | ||
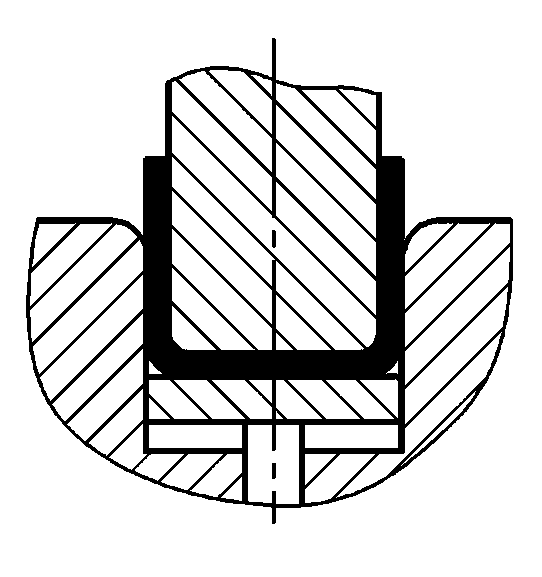 | P=(1,6Bt2σb)/(r+t)+Aq |
Tabela 5 Valor q da pressão de correção da unidade (unidade: MPa)
| Material | Espessura do material / mm | |||
| <1 | 1~3 | 3~6 | 6~10 | |
| Alumínio | 15~20 | 20~30 | 30~40 | 40~50 |
| Latão | 20~30 | 30~40 | 40~60 | 60~80 |
| 10~20 aço | 30~40 | 40~60 | 60~80 | 80~100 |
| 25~30 aço | 40~50 | 50~70 | 70~100 | 100~120 |
III. Cálculo do trabalho de flexão
O trabalho de flexão das peças de flexão em forma de V pode ser calculado com a seguinte fórmula.
Wv=mFvh
Onde
- Wv - Trabalho de dobra de peças de dobra em forma de V (J), geralmente calculado por dobra de contato;
- m - Coeficiente de correção, m=0,32 para peças de flexão em forma de V, m=0,63 para peças de flexão em forma de U;
- Fv - Força de flexão das peças de flexão em forma de V (kN), F v ou F u A força de flexão pode encontrar a fórmula de cálculo apropriada na Tabela 1 para calcular a força de flexão.
- h - Profundidade da cavidade da matriz de dobra (ou seja, curso de dobra) (mm), h também pode ser calculado com a fórmula a seguir.
h=0,5L~0,4(t+r)
Onde
- L - Distância entre os dois pontos de apoio das peças de dobra em forma de V na abertura da matriz de dobra (mm);
- t - Espessura das peças de flexão (mm);
- r - Raio de curvatura (mm).
IV. Método gráfico simplificado para força de flexão e trabalho de flexão
A Figura 2 mostra a tabela de colunas de cálculo gráfico para a força de flexão e o trabalho de flexão de peças de flexão em forma de V e em forma de U. Essa tabela é conveniente de usar, o cálculo gráfico é rápido e os resultados são próximos da realidade, adequados para uso no local.
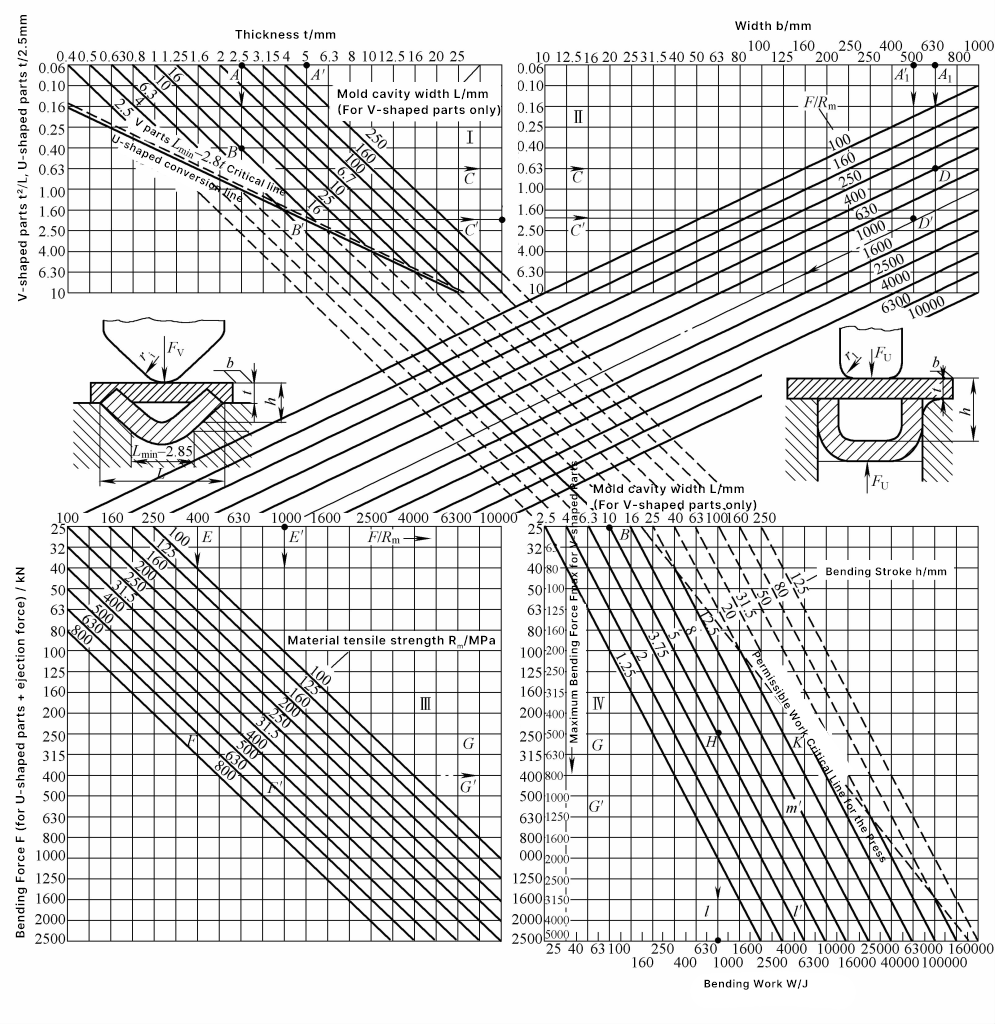
Observação: Os símbolos no gráfico significam o seguinte:
- F - Força de flexão das peças de flexão em forma de V e em forma de U (kN);
- W - Trabalho de dobra de peças de dobra em forma de V e em forma de U (J);
- H - Curso de trabalho de dobra de peças de dobra em forma de V e em forma de U (mm);
- L, L min - Largura de abertura da matriz de dobra para peças de dobra em forma de V (mm), largura mínima de abertura (mm);
- r - Raio de curvatura interno das peças de curvatura (mm);
- t - Espessura das peças de flexão (mm).
Exemplo de cálculo gráfico. Dada uma peça de dobra em forma de V com t=2,5 mm, largura de abertura da matriz de dobra L=10 mm. Na área I da Figura 2, t2/L=0,63 (veja a linha ABC). Considerando a largura da peça de flexão b=630 mm, a resistência à tração do material R m =630MPa, nas áreas II e III, encontre os valores de A1 DEF, e na área III, ao longo da linha de extensão direita, encontre a linha FG, resultando em uma força de flexão Fv =250kN.
Na área IV, considerando a pressão de endireitamento de nivelamento, a pressão total é F∑ =2F=500kN. O curso de trabalho de flexão h=0,5L=5mm, o coeficiente de correção m=0,32, portanto, o trabalho de flexão Wv =mF∑ h=800J, conforme mostrado na linha BH e na linha CHI na Figura 2.