Усилие изгиба является важной основой для проектирования процессов штамповки, выбора прессов и конструирования пресс-форм.
Поскольку величина усилия изгиба зависит не только от размеров заготовки, механических свойств материала, расстояния между опорами штампа, радиуса изгиба и зазора между пресс-формами, но и в значительной степени от метода гибки, точные расчеты с помощью методов теоретического анализа произвести сложно. Поэтому в производстве для грубого расчета силы изгиба обычно используются эмпирические формулы, приведенные в таблице 1.
I. Теоретические основы и методы расчета изгибающей силы
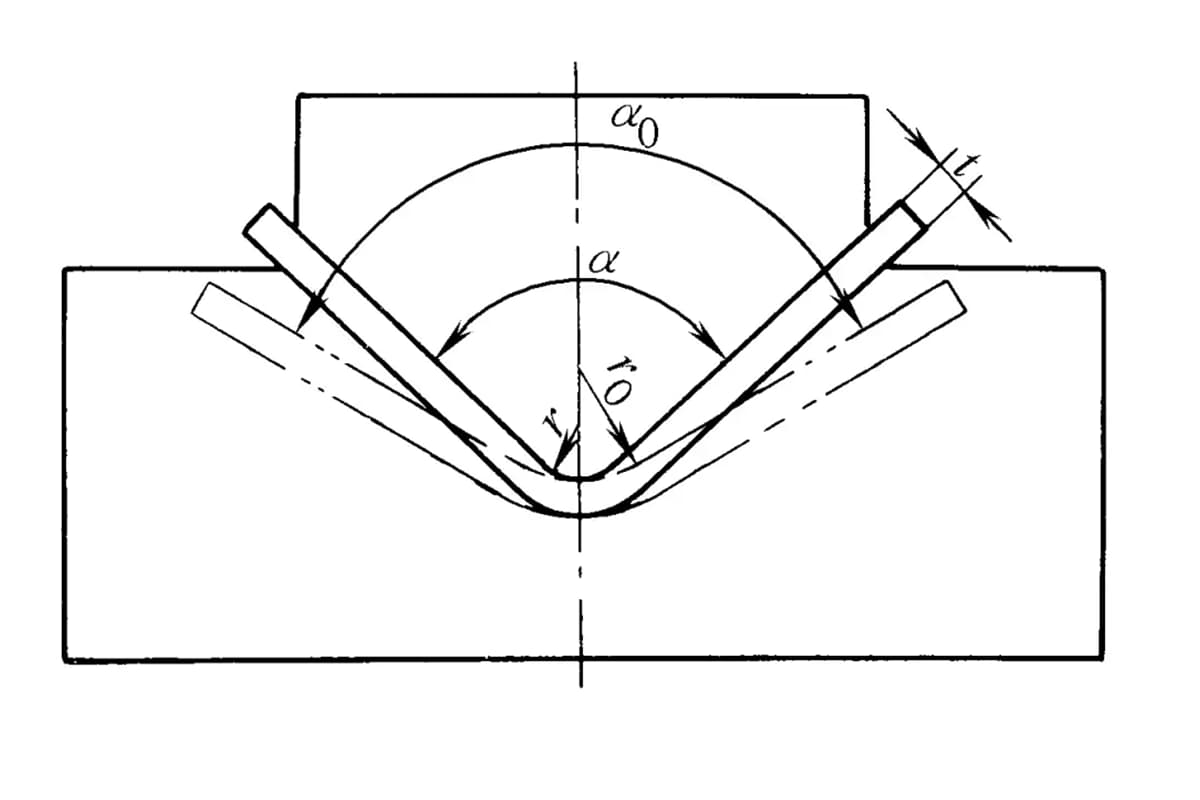
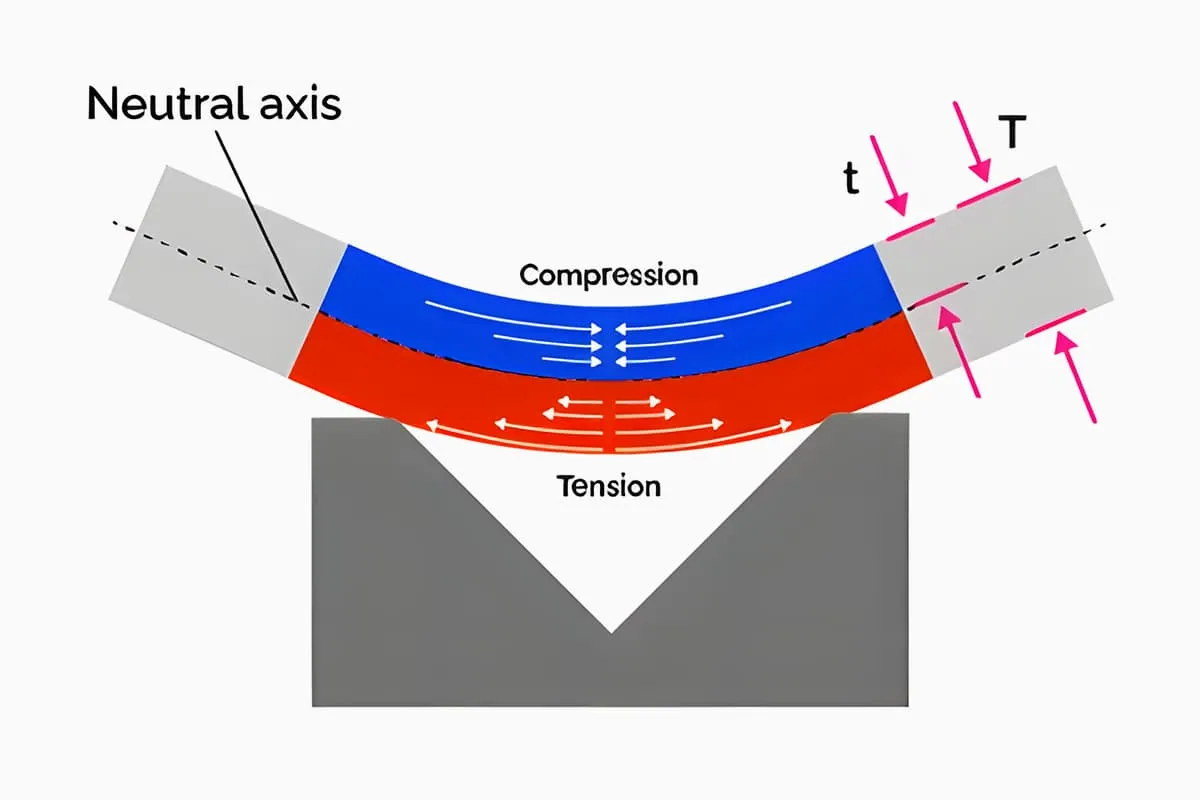
Теоретический метод расчета изгибающей силы выведен в условиях статического равновесия, когда сумма различных внешних сил, действующих на изгибаемую заготовку, равна нулю, а внешний момент, действующий на изгибаемую заготовку, равен ее внутреннему моменту сопротивления, путем обычного расчета.
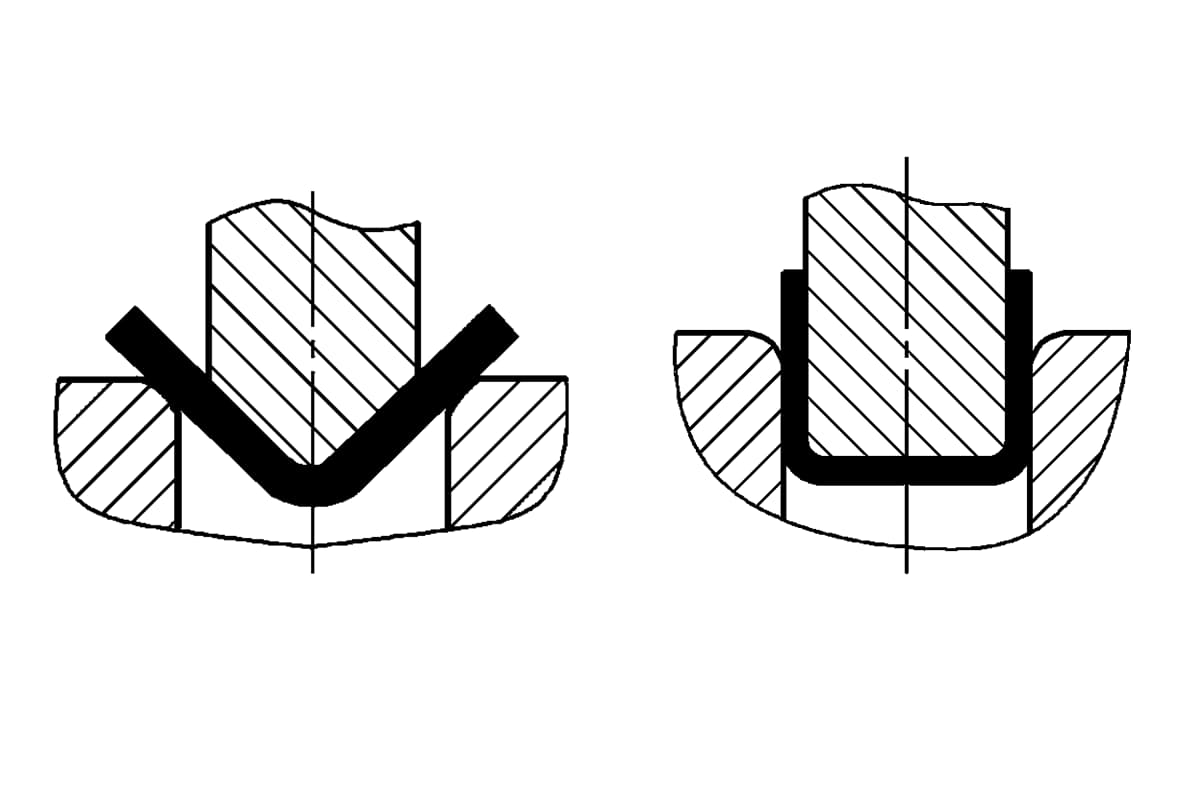
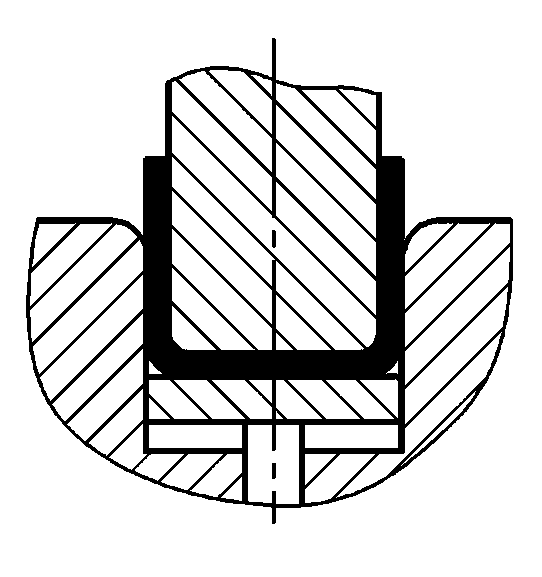
Метод гибки и конструкция штампа изменяют напряженное состояние гибочной заготовки. Различные методы гибки приводят к совершенно разным давлениям при изгибе. Если взять широко используемые V-образную и U-образную формы гибочные детали как показано на рис. 1, они могут быть сформированы путем гибки с помощью обычных гибочных штампов из цельной стали, соответственно с использованием свободной гибки, контактной гибки с расстройкой и гибки с коррекцией удара.
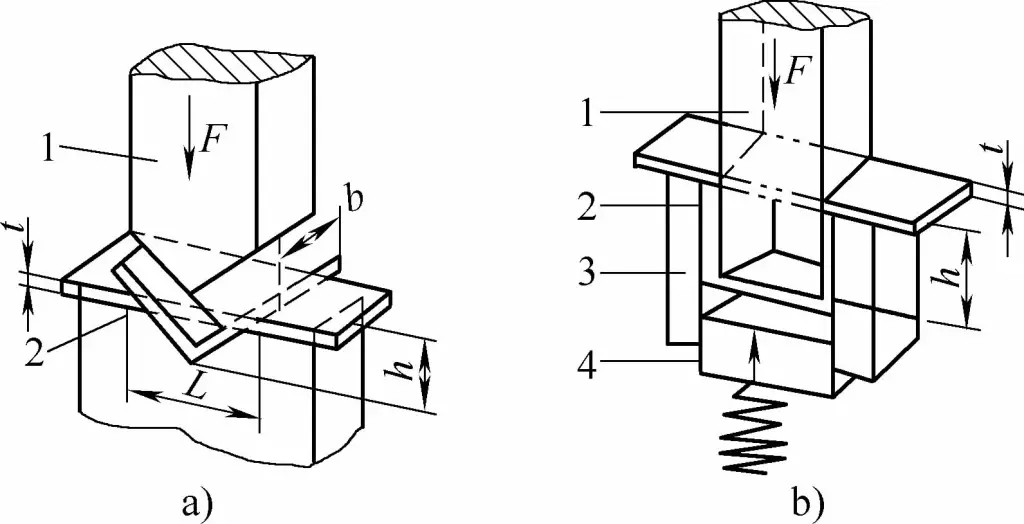
- a) V-образные гибочные детали
- b) U-образные гибочные детали
- 1 - Гибочный пуансон
- 2 - Сгибающаяся часть
- 3 - U-образный гибочный штамп
- 4 - Верхний инструмент
- L - ширина U-образного отверстия матрицы
- t - толщина изгибаемой части
- h - глубина V-образной полости гибочного штампа
V-образные гибочные детали используют сосредоточенную нагрузку в середине двух опор плоской заготовки для чистой гибки и свободной гибки, в основном используются на строительных площадках. Листогибочные детали малых и средних размеров в основном формируются контактной расстроповочной гибкой, а высокопрочные листовые заготовки средней толщины часто гнутся на фрикционных прессах с помощью ударной коррекционной гибки. Свободная гибка требует меньшего давления, без дополнительного давления, только простая сила изгиба.
II. Расчет изгибающего усилия различными методами изгиба
Формулы расчета изгибающего усилия при различных способах изгиба приведены в таблице 1.
Таблица 1 Расчетные формулы для изгибающего усилия при различных методах изгиба
| Имя | Схема | Характеристики деформации при изгибе | Формула расчета изгибающего усилия | ||
| Теория | Приблизительный | Рекомендуем | |||
| Свободный изгиб под одним углом (V-образная изгибающаяся часть) | 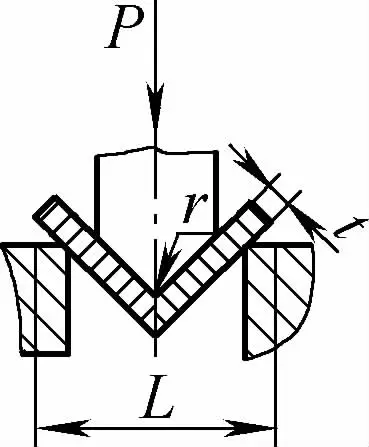 | Заготовка сгибается посередине, оказывая давление на две опоры у входа в пресс-форму, нижняя часть не соприкасается с пресс-формой | Когда 2r≤L, F=0,7bt3 Rm /(r+t) Когда 2r>L, F=2bt2 Rm /3L | F = KbtRm | F=Cbt2Rm/L |
| Одноугловой контактный изгиб (V-образные гибочные детали) | 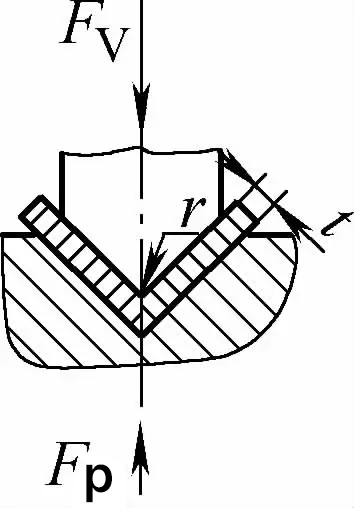 | До завершения процесса гибки гибочная заготовка находится в тесном контакте со всей полостью пресс-формы. Как правило, для гибки используется прижимная плита. зазор между матрицами больше или равно t | Когда 2r≤L, Fv =0.7bt2 Rm /(r+t)+Fp Когда 2r>L, Fv =2bt2 Rm /3L+Fp | Fv=KbtRm +Fp | Fv=2Cbt2Rm/L |
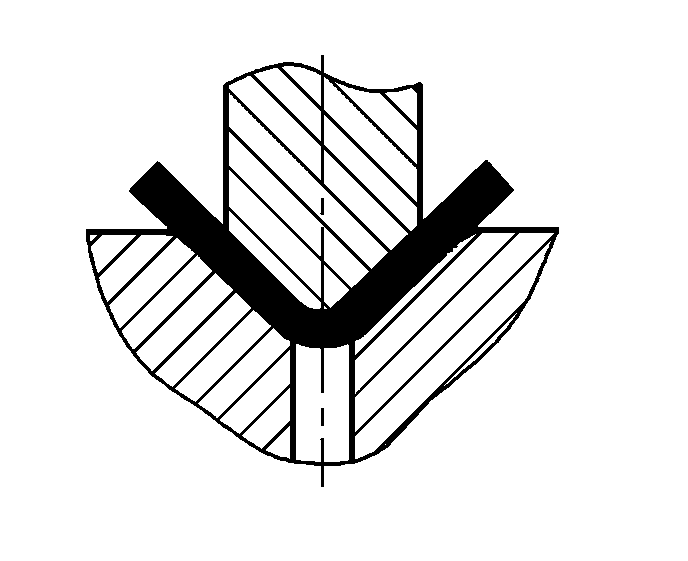
| Одноугловой контакт с коррекцией ударного изгиба (V-образные изгибаемые части) | 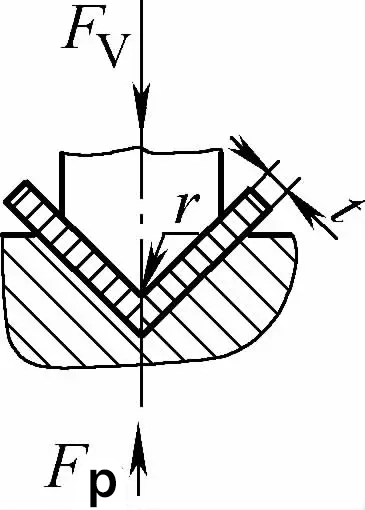 | Основанный на контактной гибке, он также выполняет функцию коррекции удара. Зазор между гибочными штампами обычно меньше или равен t | Fv=0.7bt2Rm/L+Fp+qAb | Fv=1,3qAb | Fv=1,39qAb |
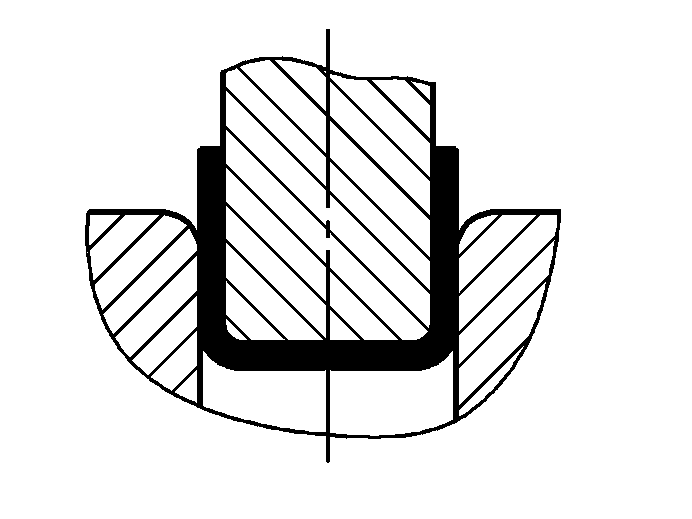
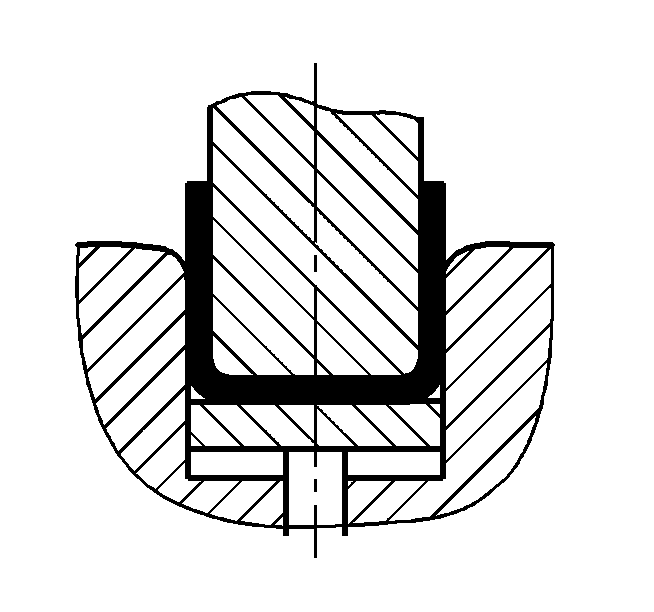
| Свободный изгиб с двойным углом (U-образные гибочные детали) | 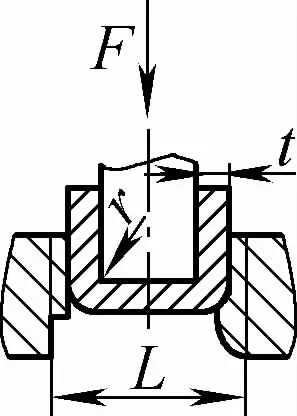 | Гибочная заготовка сгибается посередине за счет давления на две опоры у входа в пресс-форму, нижняя часть заготовки не соприкасается с пресс-формой | Когда 2r≤L, F=0,7bt 2 Rm /(r+t) Когда 2r>L, F=2bt 2 Rm /3L | F =KbtRm | F=0,4CKbtRm |
| Контактная гибка с двойным углом (U-образные гибочные детали) | 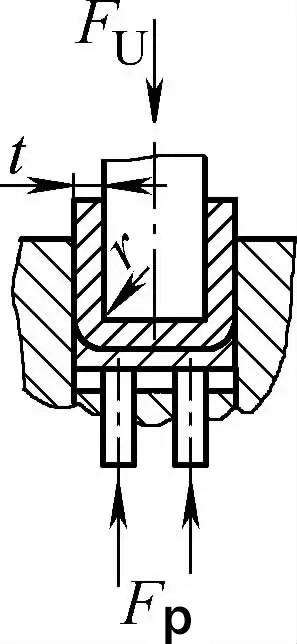 | При изгибе используется прижимная пластина или зазор, равный или немного превышающий t, но функция коррекции удара отсутствует. | Когда 2r≤L, Fu =0.7bt2Rm /(r+t)+Fp Когда 2r>L, Fu =2bt2Rmn/3L+Fp | Fu =KbtRm +Fp | Fu=0,5CbtRm |
| Двухугловой контакт с коррекцией ударного изгиба (U-образные изгибаемые части) | 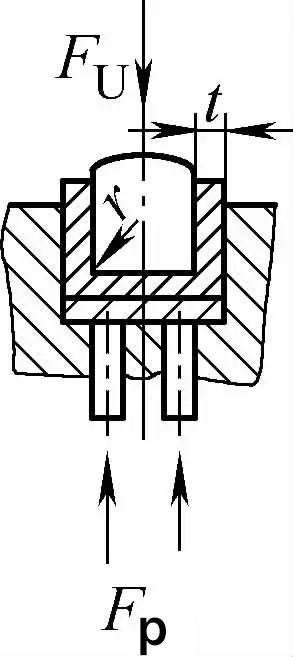 | Во время гибки зазор, меньший или равный t, используется с прижимной пластиной (верхней пластиной) и также выполняет функцию коррекции удара. | Fu=0.7bt2Rmn/L+Fp+qAb | Fu=1,3qAb | Fu=1,3qAb |
Примечание: Значения символов в таблице приведены ниже:
- b - ширина изгибаемой части (мм);
- R - предел прочности материала гибочной части (МПа);
- L - длина гибочной заготовки в точках опоры по обе стороны от отверстия гибочного штампа (мм);
- C - коэффициент, для одноуглового изгиба L>10t, C=1; для двухуглового изгиба r=t, C=1; n-число углов изгиба (штук);
- A - площадь опоры изгибаемой части (мм²);
- F - плоское корректирующее давление (кН), обычно 30%~100% от силы изгиба;
- K - коэффициент типа материала, значение можно найти в таблице 2;
- q - давление коррекции единицы (удара) (МПа), значение можно найти в таблице 3.
Таблица 2 Коэффициент типа материала K
| Материал | Соотношение L/t | |||||
| 3 | 10 | 15 | 20 | 25 | 30 | |
| 10 сталь, 15 сталь, латунь, алюминий (мягкий) | 0.23 | 0.18 | 0.12 | 0.09 | 0.073 | 0.060 |
| 20 сталь, 25 сталь, закаленный алюминий | 0.21 | 0.17 | 0.11 | 0.08 | 0.070 | 0.057 |
| 20 сталь, 25 сталь, 40 сталь, сверхпрочный алюминий | 0.20 | 0.16 | 0.10 | 0.08 | 0.065 | 0.053 |
Таблица 3 Приблизительное значение корректирующего давления q при изгибе (единицы измерения: МПа)
| Материал | Толщина гибочного материала t/мм | |
| ≤3 | >3~10 | |
| Алюминий | 30~40 | 50~60 |
| Латунь | 60~80 | 80~100 |
| 10 сталь, 15 сталь, 20 сталь | 80~100 | 100~120 |
| 25 сталь, 30 сталь, 35 сталь | 100~120 | 120~150 |
Формулы для расчета изгибающей силы
Таблица 4 Эмпирические формулы для расчета изгибающей силы
| Метод сгибания | Схема | Эмпирические формулы | Примечания |
| Свободное сгибание | 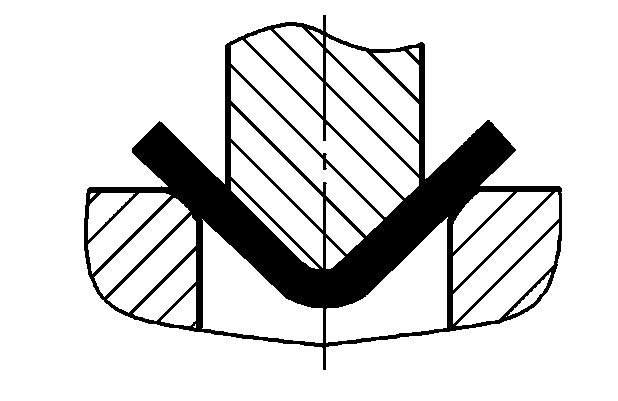 | P=(0,8Bt2σb)/(r+t) | где P-общая изгибающая сила (Н) B - ширина изогнутой части (мм) t - толщина материала (мм) σb-Прочность на разрыв (МПа) r-Inner радиус изгиба (мм) A-Зона проекции корректирующей части (мм2 ) Давление коррекции единицы (МПа), его значение см. в таблице 5 |
 | P=(0,9Bt2σb)/(r+t) | ||
| Сгибание с коррекцией | 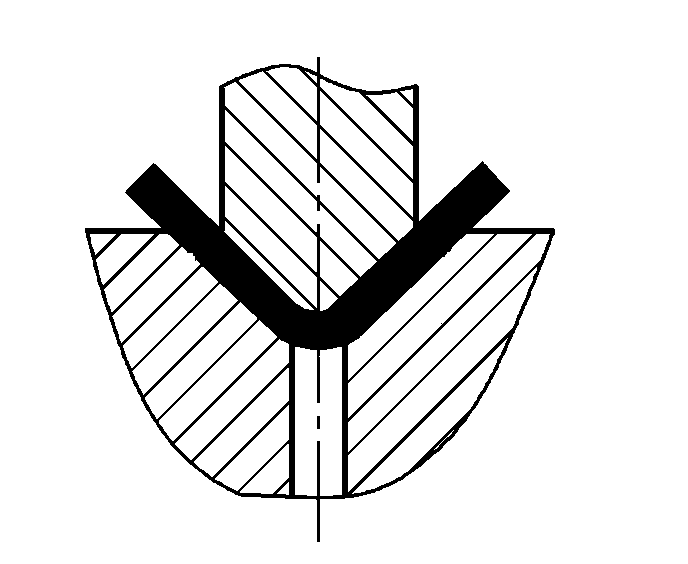 | P=(1,4Bt2σb)/(r+t) | |
 | P=(1,6Bt2σb)/(r+t) | ||
 | P=(1,4Bt2σb)/(r+t)+Aq | ||
 | P=(1,6Bt2σb)/(r+t)+Aq |
Таблица 5 Значение корректирующего давления q (единицы измерения: МПа)
| Материал | Толщина материала / мм | |||
| <1 | 1~3 | 3~6 | 6~10 | |
| Алюминий | 15~20 | 20~30 | 30~40 | 40~50 |
| Латунь | 20~30 | 30~40 | 40~60 | 60~80 |
| 10~20 сталь | 30~40 | 40~60 | 60~80 | 80~100 |
| 25~30 сталь | 40~50 | 50~70 | 70~100 | 100~120 |
III. Расчет работы на изгиб
Работа гибки V-образных гибочных деталей может быть рассчитана по следующей формуле.
Wv=mFvh
Где
- Wv - Работа гибки V-образных гибочных деталей (J), как правило, рассчитывается методом контактной расстропочной гибки;
- m - поправочный коэффициент, m=0,32 для V-образных изгибаемых деталей, m=0,63 для U-образных изгибаемых деталей;
- Fv - Изгибающее усилие V-образных изгибаемых частей (кН), F v или F u Для расчета изгибающего усилия можно найти соответствующую формулу расчета в таблице 1.
- h - глубина полости гибочного штампа (т.е. ход гиба) (мм), h также можно рассчитать по следующей формуле.
h=0.5L~0.4(t+r)
Где
- L - расстояние между двумя точками опоры V-образных гибочных деталей на отверстии гибочного штампа (мм);
- t - толщина изгибаемых частей (мм);
- r - радиус изгиба (мм).
IV. Упрощенный графический метод определения изгибающей силы и работы при изгибе
На рисунке 2 показана графическая расчетная колонная диаграмма для гибочного усилия и работы гибки V-образных и U-образных гибочных деталей. Эта таблица удобна в использовании, графический расчет выполняется быстро, а результаты близки к реальности и подходят для использования на месте.
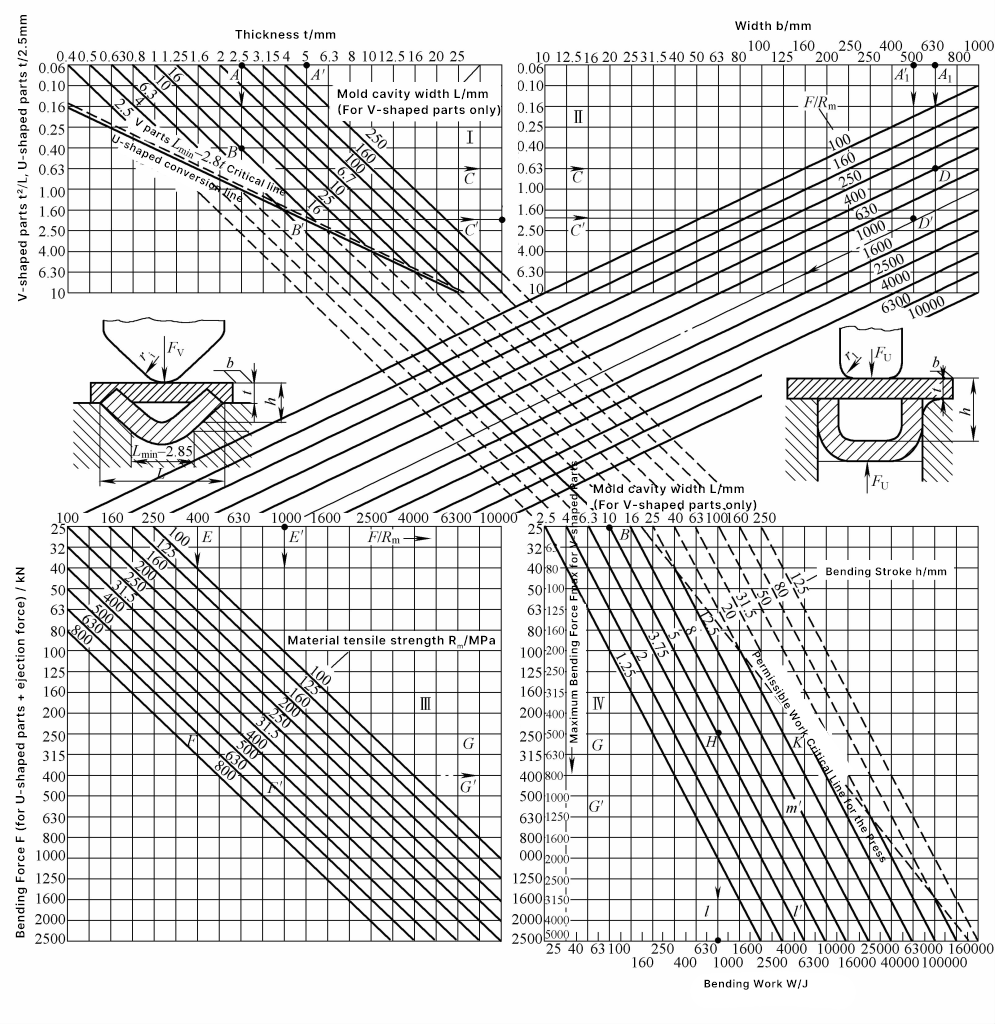
Примечание: Символы в таблице означают следующее:
- F - усилие изгиба V-образной и U-образной изгибаемых частей (кН);
- W - работа по гибке V-образных и U-образных гибочных деталей (J);
- H - рабочий ход гибки V-образных и U-образных гибочных деталей (мм);
- L, L мин - Ширина проема гибочного штампа для V-образных гибочных деталей (мм), минимальная ширина проема (мм);
- r - внутренний радиус изгиба гибочных деталей (мм);
- t - толщина изгибаемых частей (мм).
Пример графического расчета. Дана V-образная гибочная деталь с t=2,5 мм, ширина отверстия гибочного штампа L=10 мм. В области I на рисунке 2, t2/L=0,63 (см. линию ABC). Учитывая ширину изгибаемой части b=630 мм, предел прочности материала R m =630МПа, в областях II и III найдите A1 DEF, а в области III по правой линии продолжения найдите линию FG, в результате чего возникает изгибающая сила Fv =250 кН.
В зоне IV, учитывая выравнивающее давление, полное давление равно F∑ =2F=500кН. Рабочий ход гиба h=0,5L=5мм, коэффициент коррекции m=0,32, таким образом, работа гиба Wv =mF∑ h=800 Дж, как показано на линии BH и линии CHI на рис. 2.