Bükme kuvveti, damgalama işlemlerinin tasarlanması, preslerin seçilmesi ve kalıpların tasarlanması için önemli bir temeldir.
Bükme kuvvetinin büyüklüğü sadece işlenmemiş parçanın boyutu, malzemenin mekanik özellikleri, kalıbın destekleri arasındaki mesafe, bükme yarıçapı ve kalıplar arasındaki boşlukla değil, aynı zamanda bükme yöntemiyle de büyük ölçüde ilişkili olduğundan, teorik analiz yöntemlerini kullanarak doğru hesaplamalar yapmak zordur. Bu nedenle, üretimde, Tablo 1'de listelenen ampirik formüller genellikle bükme kuvvetinin kaba bir hesaplaması için kullanılır.
I. Eğilme kuvveti için teorik hesaplama temeli ve yöntemleri
Eğilme kuvvetinin teorik hesaplama yöntemi, eğilme boşluğuna etki eden çeşitli dış kuvvetlerin toplamının sıfır olduğu ve eğilme boşluğuna etki eden dış torkun iç direnç torkuna eşit olduğu statik denge koşulları altında geleneksel hesaplama yoluyla türetilmiştir.
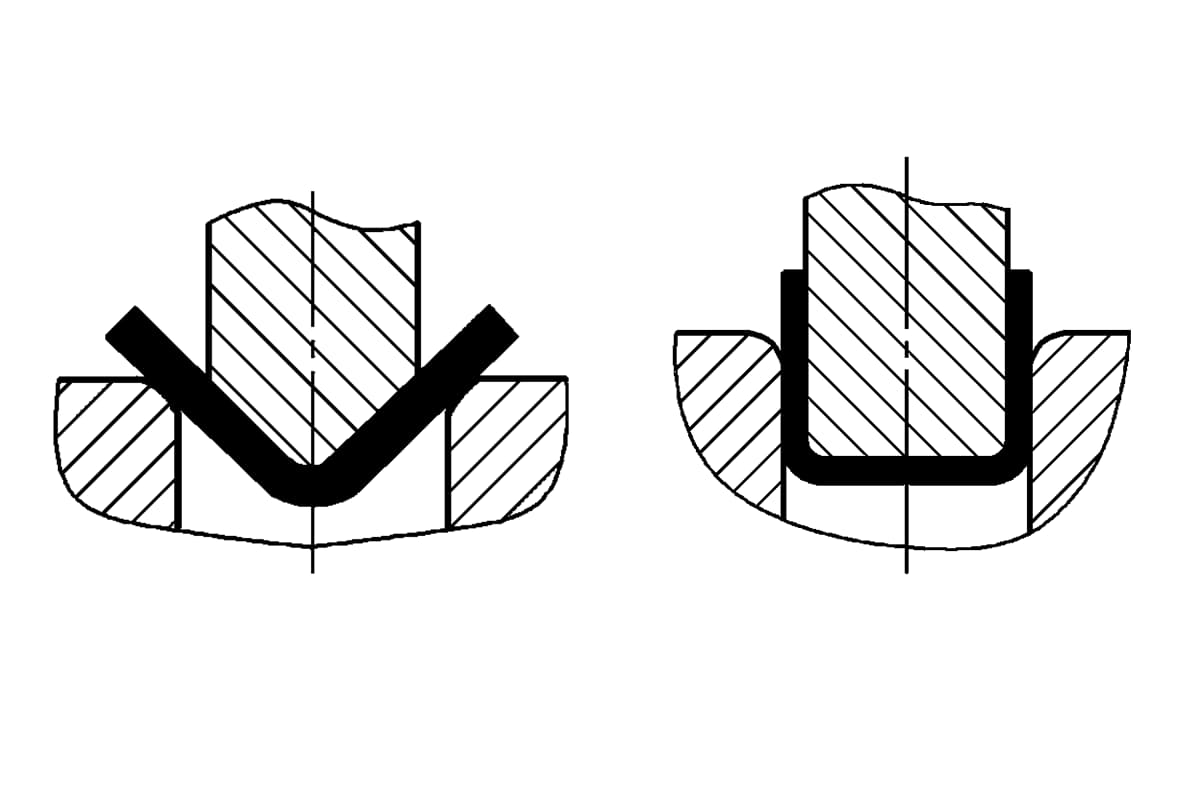
Bükme yöntemi ve kalıp yapısı, bükme boşluğunun gerilim durumunu değiştirecektir. Farklı bükme yöntemleri büyük ölçüde farklı bükme basınçlarına neden olur. Yaygın olarak kullanılan V şekilli ve U şekilli bükme parçalari Örnek olarak, Şekil 1'de gösterildiği gibi, sıradan tam çelik bükme kalıpları ile sırasıyla serbest bükme, temaslı üzücü bükme ve darbe düzeltme bükme kullanılarak bükülerek oluşturulabilirler.
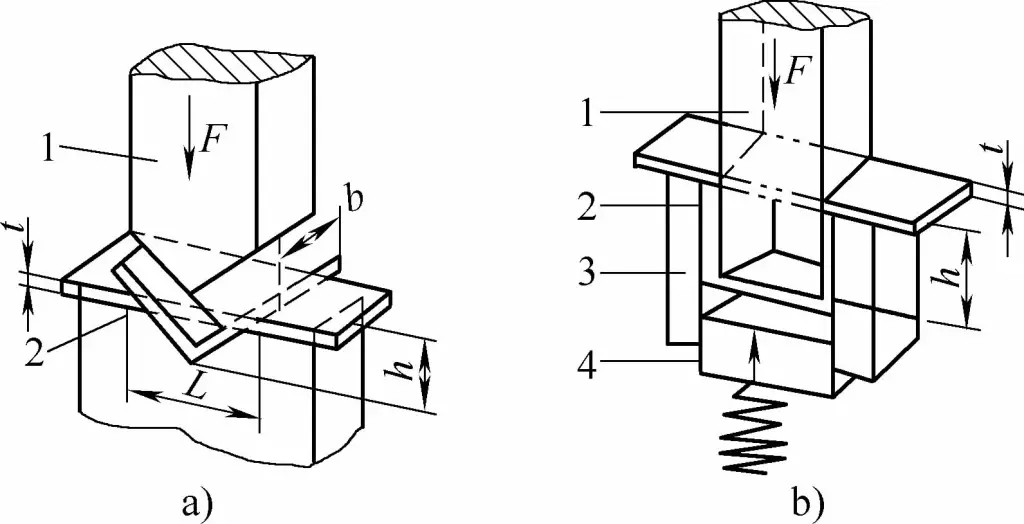
- a) V şekilli bükme parçaları
- b) U şeklinde bükülen parçalar
- 1 - Bükme zımbası
- 2 - Bükme parçası
- 3 - U şeklinde bükme kalıbı
- 4 - Üst takım
- L - U şeklindeki kalıp açıklığının genişliği
- t - Bükülen parçanın kalınlığı
- h - V şeklindeki bükme kalıbı boşluğunun derinliği
V şeklindeki bükme parçaları, çoğunlukla şantiyelerde kullanılan saf bükme ve serbest bükme için düz bir boşluğun iki desteğinin ortasında konsantre bir yük kullanır. Çevrimiçi, küçük ve orta ölçekli sac bükme parçaları çoğunlukla temaslı üzücü bükme ile oluşturulur ve yüksek mukavemetli orta kalınlıkta plaka bükme parçaları genellikle darbe düzeltme bükme kullanılarak sürtünme preslerinde bükülür. Serbest bükme, ek basınç olmadan, sadece basit bükme kuvveti ile daha az basınç gerektirir.
II. Çeşitli eğme yöntemleri ile eğme kuvvetinin hesaplanması
Çeşitli eğme yöntemlerine göre eğme kuvveti hesaplama formülleri Tablo 1'de gösterilmiştir.
Tablo 1 Çeşitli eğme yöntemlerine göre eğme kuvveti hesaplama formülleri
| İsim | Şematik | Eğilme deformasyonunun özellikleri | Eğilme kuvveti hesaplama formülü | ||
| Teorik | Yaklaşık | Tavsiye edilir | |||
| Tek açılı serbest bükme (V şeklinde bükme parçası) | 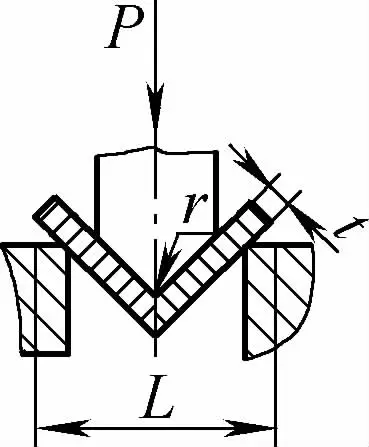 | İşlenmemiş parça, kalıp girişindeki iki destek üzerine baskı uygulanarak ortadan aşağı doğru bükülür, alt kısım kalıba temas etmez | 2r≤L olduğunda, F=0,7bt3 Rm /(r+t) 2r>L olduğunda, F=2bt2 Rm /3L | F = KbtRm | F=Cbt2Rm/L |
| Tek açılı temaslı bükme (V şekilli bükme parçaları) | 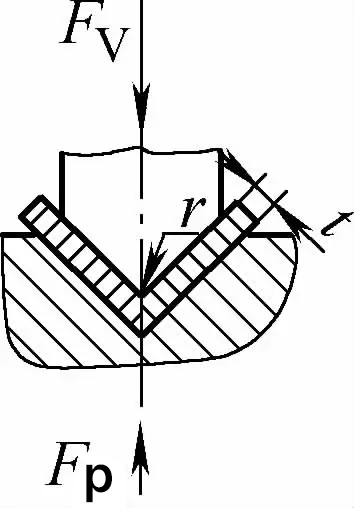 | Bükme işlemi tamamlanmadan önce, bükme boşluğu tüm kalıp boşluğu ile yakın temas halindedir. Bükme işlemini yapmak için genellikle bir baskı plakası kullanılır. kalıp boşluğu t'den büyük veya eşit | 2r≤L olduğunda, Fv =0.7bt2 Rm /(r+t)+Fp 2r>L olduğunda, Fv =2bt2 Rm /3L+Fp | Fv=KbtRm +Fp | Fv=2Cbt2Rm/L |
| Darbe düzeltmeli bükme ile tek açılı temas (V şeklinde bükme parçaları) | 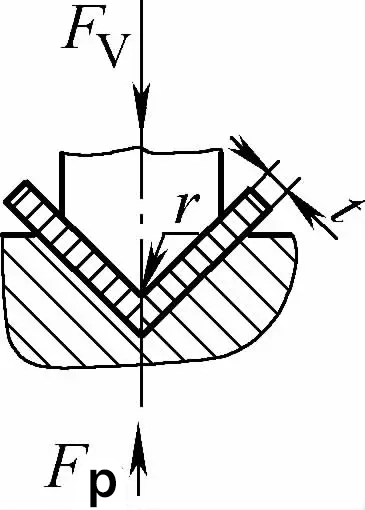 | Temaslı bükmeye dayalı olarak, darbe düzeltme işlevine de sahiptir. Bükme kalıbı boşluğu genellikle t'ye eşit veya daha azdır | Fv=0.7bt2Rm/L+Fp+qAb | Fv=1.3qAb | Fv=1.39qAb |
| Çift açılı serbest bükme (U şeklinde bükme parçaları) | 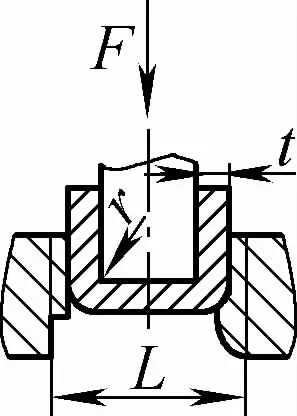 | Bükme boşluğu, kalıp girişindeki iki destek üzerine basınç uygulanarak ortadan bükülür, boşluğun alt kısmı kalıba temas etmez | 2r≤L olduğunda, F=0,7bt 2 Rm /(r+t) 2r>L olduğunda, F=2bt 2 Rm /3L | F =KbtRm | F=0,4CKbtRm |
| Çift açılı temaslı bükme (U şeklinde bükme parçaları) | 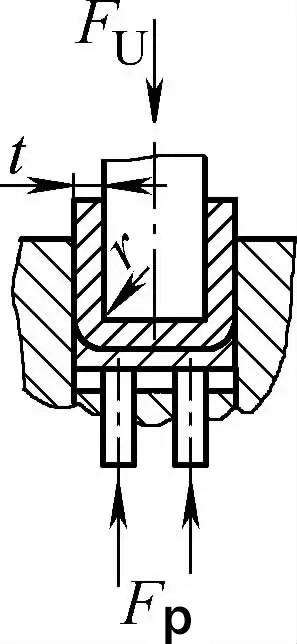 | Bükme sırasında bir baskı plakası kullanılır veya t'ye eşit veya biraz daha büyük bir boşluk kullanılır, ancak darbe düzeltme işlevi yoktur | 2r≤L olduğunda, Fu =0.7bt2Rm /(r+t)+Fp 2r>L olduğunda, Fu =2bt2Rmn/3L+Fp | Fu =KbtRm +Fp | Fu=0,5CbtRm |
| Darbe düzeltmeli bükme ile çift açılı temas (U şeklinde bükme parçaları) | 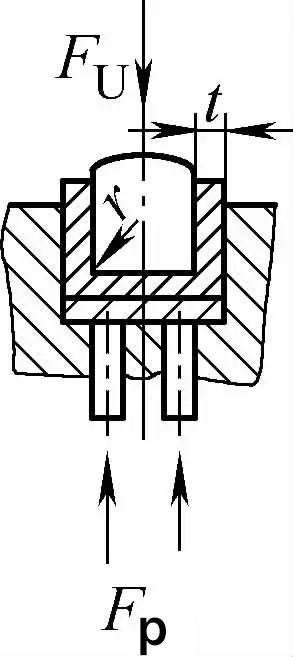 | Bükme sırasında, t'ye eşit veya daha küçük bir bükme boşluğu bir baskı plakası (üst plaka) ile kullanılır ve aynı zamanda darbe düzeltme işlevine sahiptir | Fu=0.7bt2Rmn/L+Fp+qAb | Fu=1.3qAb | Fu=1.3qAb |
Not: Tablodaki sembollerin anlamları aşağıdaki gibidir:
- b - bükme parçasının genişliği (mm);
- R - bükülen parça malzemesinin çekme dayanımı (MPa);
- L - bükme kalıbı açıklığının her iki tarafındaki destek noktalarında bükme boşluğunun uzunluğu (mm);
- C - katsayı, tek açılı bükme için L>10t, C=1; çift açılı bükme için r=t, C=1; n-bükme açısı sayısı (adet);
- A - bükülen parçanın yatak alanı (mm²);
- F - düz düzeltme basıncı (kN), genellikle eğilme kuvvetinin 30%~100%'si;
- K - malzeme tipi katsayısı, değer Tablo 2'de bulunabilir;
- q - birim (darbe) düzeltme basıncı (MPa), değer Tablo 3'te bulunabilir.
Tablo 2 Malzeme tipi katsayısı K değeri
| Malzeme | Oran L/t | |||||
| 3 | 10 | 15 | 20 | 25 | 30 | |
| 10 çelik, 15 çelik, pirinç, alüminyum (yumuşak) | 0.23 | 0.18 | 0.12 | 0.09 | 0.073 | 0.060 |
| 20 çelik, 25 çelik, sertleştirilmiş alüminyum | 0.21 | 0.17 | 0.11 | 0.08 | 0.070 | 0.057 |
| 20 çelik, 25 çelik, 40 çelik, süper sert alüminyum | 0.20 | 0.16 | 0.10 | 0.08 | 0.065 | 0.053 |
Tablo 3 Bükme sırasında birim (darbe) düzeltme basıncı q'nun yaklaşık değeri (birim: MPa)
| Malzeme | Bükme malzemesi kalınlığı t/mm | |
| ≤3 | >3~10 | |
| Alüminyum | 30~40 | 50~60 |
| Pirinç | 60~80 | 80~100 |
| 10 çelik, 15 çelik, 20 çelik | 80~100 | 100~120 |
| 25 çelik, 30 çelik, 35 çelik | 100~120 | 120~150 |
Eğilme kuvvetini hesaplamak için formüller
Tablo 4 Eğilme kuvvetinin hesaplanması için ampirik formüller
| Bükme yöntemi | Şematik | Ampirik formüller | Notlar |
| Serbest bükme | 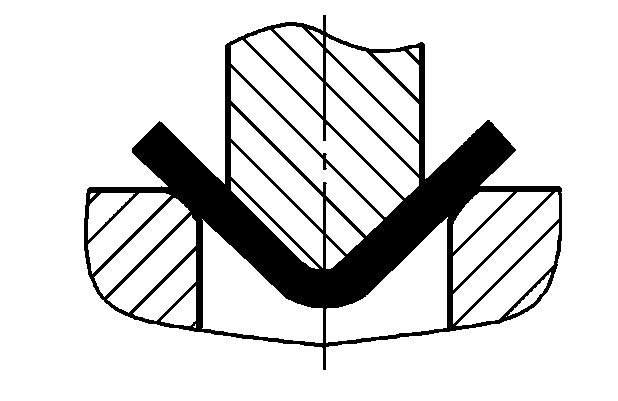 | P=(0.8Bt2σb)/(r+t) | nerede P-Toplam eğilme kuvveti (N) B-Bükülmüş parçanın genişliği (mm) t-Malzeme kalınlığı (mm) σb-Çekme dayanımı (MPa) r-İç bükülme yarıçapı (mm) A-Düzeltme parçası projeksiyon alanı (mm2 ) Birim düzeltme basıncı (MPa), değeri için Tablo 5'e bakınız |
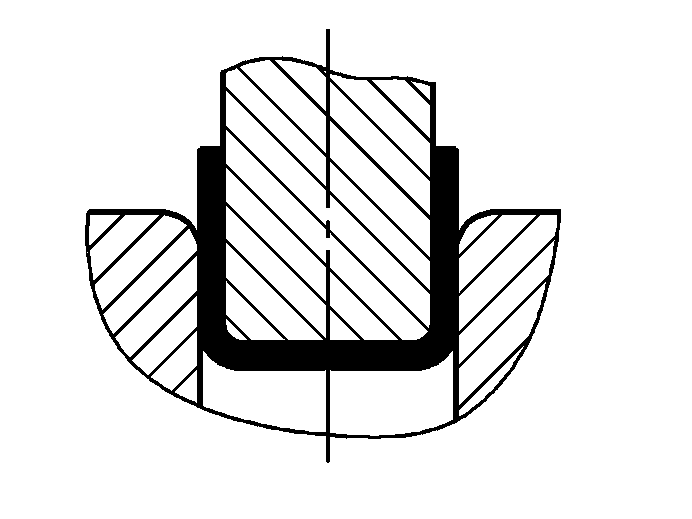 | P=(0.9Bt2σb)/(r+t) | ||
| Düzeltme ile bükme | 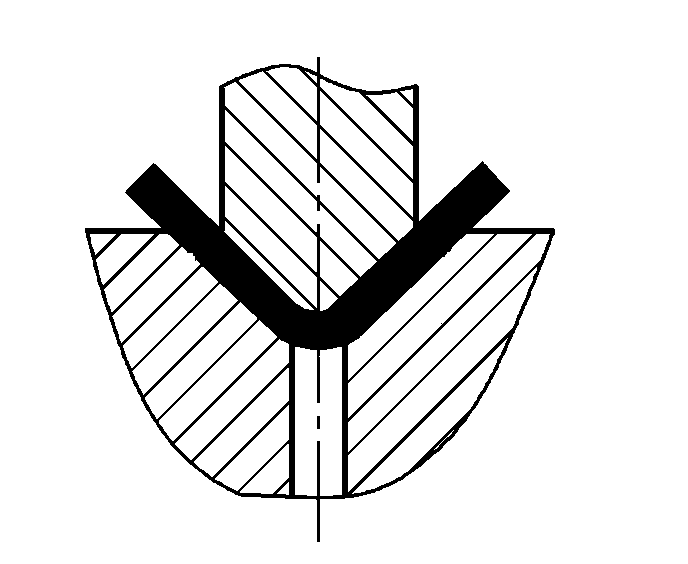 | P=(1.4Bt2σb)/(r+t) | |
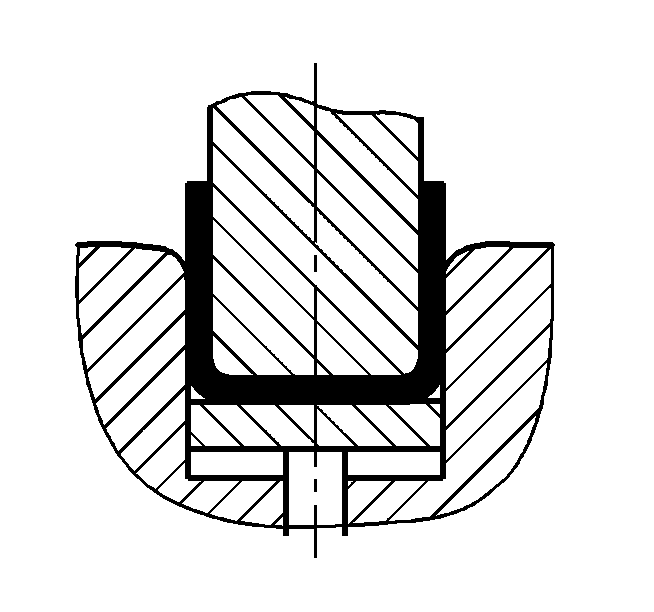 | P=(1.6Bt2σb)/(r+t) | ||
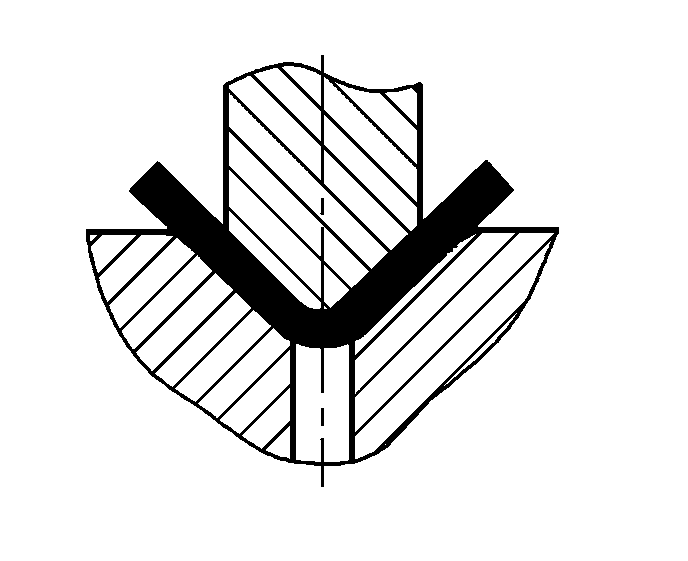 | P=(1.4Bt2σb)/(r+t)+Aq | ||
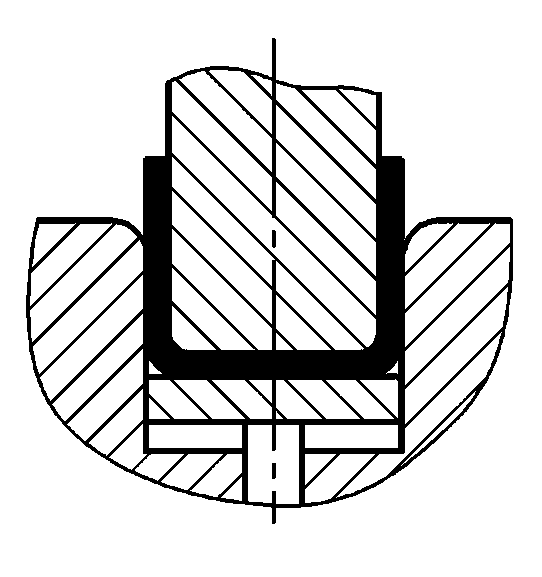 | P=(1.6Bt2σb)/(r+t)+Aq |
Tablo 5 Birim düzeltme basıncı q değeri (birim: MPa)
| Malzeme | Malzeme kalınlığı / mm | |||
| <1 | 1~3 | 3~6 | 6~10 | |
| Alüminyum | 15~20 | 20~30 | 30~40 | 40~50 |
| Pirinç | 20~30 | 30~40 | 40~60 | 60~80 |
| 10~20 çelik | 30~40 | 40~60 | 60~80 | 80~100 |
| 25~30 çelik | 40~50 | 50~70 | 70~100 | 100~120 |
III. Bükme işinin hesaplanması
V şeklindeki bükme parçalarının bükme işi aşağıdaki formül kullanılarak hesaplanabilir.
Wv=mFvh
Nerede
- Wv - V şeklindeki bükme parçalarının bükme işi (J), genellikle temaslı üzgün bükme ile hesaplanır;
- m - Düzeltme katsayısı, V şekilli bükme parçaları için m=0.32, U şekilli bükme parçaları için m=0.63;
- Fv - V şeklindeki bükme parçalarının bükme kuvveti (kN), F v veya F u Eğilme kuvveti, eğilme kuvvetini hesaplamak için Tablo 1'de uygun hesaplama formülünü bulabilir.
- h - Bükme kalıbı boşluğunun derinliği (yani, bükme stroku) (mm), h aşağıdaki formül kullanılarak da hesaplanabilir.
h=0.5L~0.4(t+r)
Nerede
- L - Bükme kalıbının açıklığındaki V şeklindeki bükme parçalarının iki destek noktası arasındaki mesafe (mm);
- t - Bükülen parçaların kalınlığı (mm);
- r - Bükülme yarıçapı (mm).
IV. Eğilme kuvveti ve eğilme işi için basitleştirilmiş grafik yöntemi
Şekil 2, V-şekilli ve U-şekilli bükme parçalarının bükme kuvveti ve bükme işi için grafik hesaplama sütun grafiğini göstermektedir. Bu çizelgenin kullanımı uygundur, grafiksel hesaplama hızlıdır ve sonuçlar gerçeğe yakındır, yerinde kullanım için uygundur.
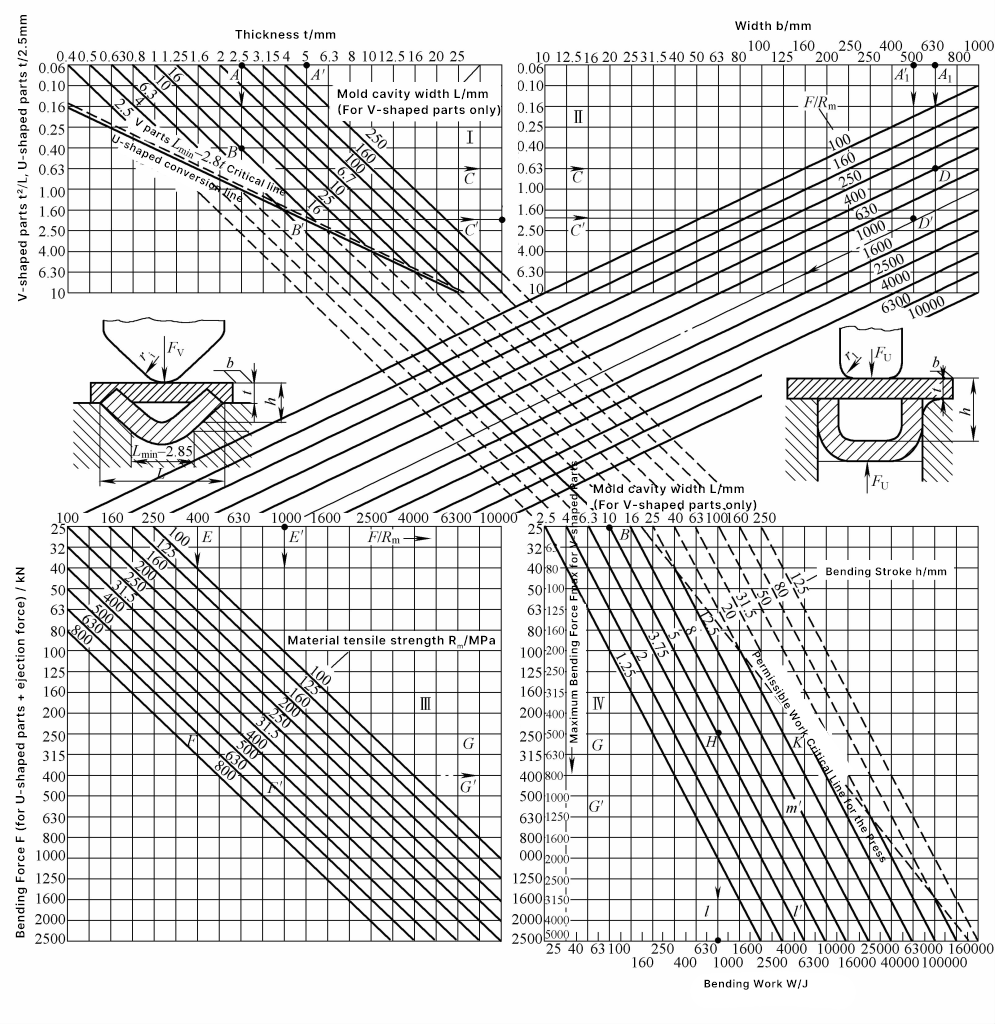
Not: Tablodaki semboller aşağıdaki anlamlara gelmektedir:
- F - V şekilli ve U şekilli bükme parçalarının bükme kuvveti (kN);
- W - V şekilli ve U şekilli bükme parçalarının bükme işi (J);
- H - V şekilli ve U şekilli bükme parçalarının bükme çalışma stroku (mm);
- L, L min - V şekilli bükme parçaları için bükme kalıbının açılma genişliği (mm), minimum açılma genişliği (mm);
- r - Bükme parçalarının iç bükme yarıçapı (mm);
- t - Bükülen parçaların kalınlığı (mm).
Grafiksel hesaplama örneği. t=2.5mm, bükme kalıbının açıklık genişliği L=10mm olan V şeklinde bir bükme parçası verilmiştir. Şekil 2'deki I alanında, t2/L=0,63 (ABC çizgisine bakınız). Bükme parçasının genişliği b=630mm olarak verildiğinde, malzemenin çekme dayanımı R m =630MPa, II ve III bölgelerinde, A1 DEF çizgisini ve III. alanda, sağ uzatma çizgisi boyunca, FG çizgisini bulun, sonuçta bir eğilme kuvveti Fv =250kN.
IV. alanda, tesviye doğrultma basıncı dikkate alındığında, toplam basınç F∑ =2F=500kN. Bükme çalışma stroku h=0.5L=5mm, düzeltme katsayısı m=0.32, dolayısıyla bükme işi Wv =mF∑ h=800J, Şekil 2'deki BH çizgisi ve CHI çizgisinde gösterildiği gibi.