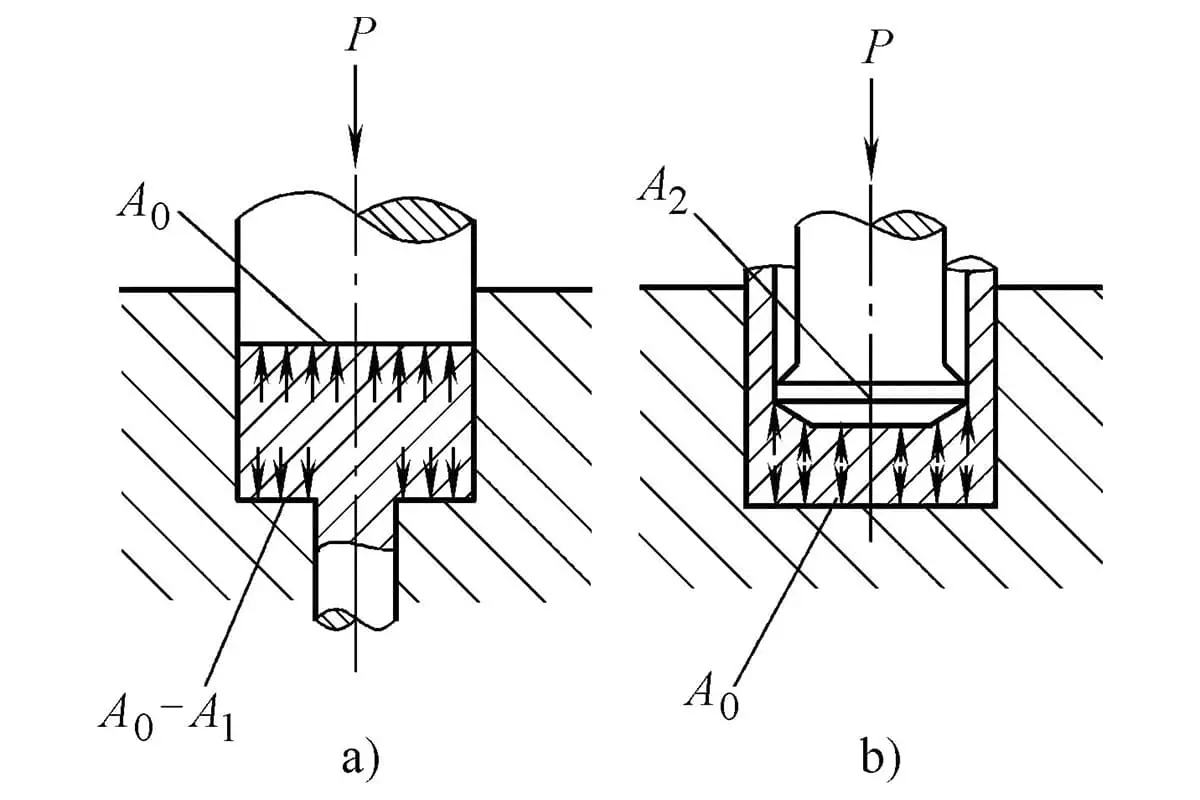
Soğuk ekstrüzyon prosesinde, bir dizi teknolojik faktör nedeniyle, ekstrüzyon kuvvetinin doğru bir şekilde hesaplanması zordur. Bu durum özellikle karmaşık şekilli parçalar için geçerlidir ve bunlar için iyi belirlenmiş hesaplama yöntemleri veya pratik, güvenilir formüller veya çizelgeler yoktur.
Şu anda, soğuk ekstrüzyon sırasında ekstrüzyon kuvvetini hesaplamak için kullanılan yaygın yöntemler arasında basit hesaplamalar, grafik hesaplamalar ve grafik analiz yöntemleri bulunmaktadır.
Basit Hesaplama Yöntemi
Çeşitli farklı malzemeler için birim ekstrüzyon kuvvetinin yaklaşık değeri Tablo 3-13'te bulunabilir ve daha sonra yaklaşık bir ekstrüzyon kuvveti elde etmek için ekstrüzyonun gerçek çalışma alanı ile çarpılabilir. Formül şöyledir:
P = pA (3-9)
Nerede?
- A, ekstrüzyonun çalışma alanıdır (mm²). Karmaşık şekilli parçalar için hesaplama, öngörülen alana göre yapılır.
- p, Tablo 3-13'te bulunabilen birim ekstrüzyon kuvvetidir (MPa).
Uygulama, yukarıdaki ampirik verilerle yapılan tahminin gerçek duruma yakın olduğunu ve temelde gereksinimi karşılayabildiğini kanıtlamıştır.
Grafiksel Hesaplama Yöntemi
Nomogram yöntemi olarak da bilinen bu yaklaşım, soğuk ekstrüzyon işlemi sırasında metalin düzgün bir deformasyon durumuna sahip olduğunu varsayar. Ekstrüzyon kesitinin küçülme oranı, işlenmemiş parçanın boyutu, malzemenin mekanik özellikleri ve kalıbın çalışan kısmının şekli gibi faktörleri dikkate alır.
Grafiksel hesaplama yöntemini kullanmanın bir diğer koşulu da işlenmemiş parçanın ekstrüzyondan önce yumuşatma, yüzey işleme ve yağlama işlemlerinden geçmesidir.
(1) Çelik Malzemelerin Birim Ekstrüzyon Kuvvetinin Hesaplanması için Grafik Yöntem
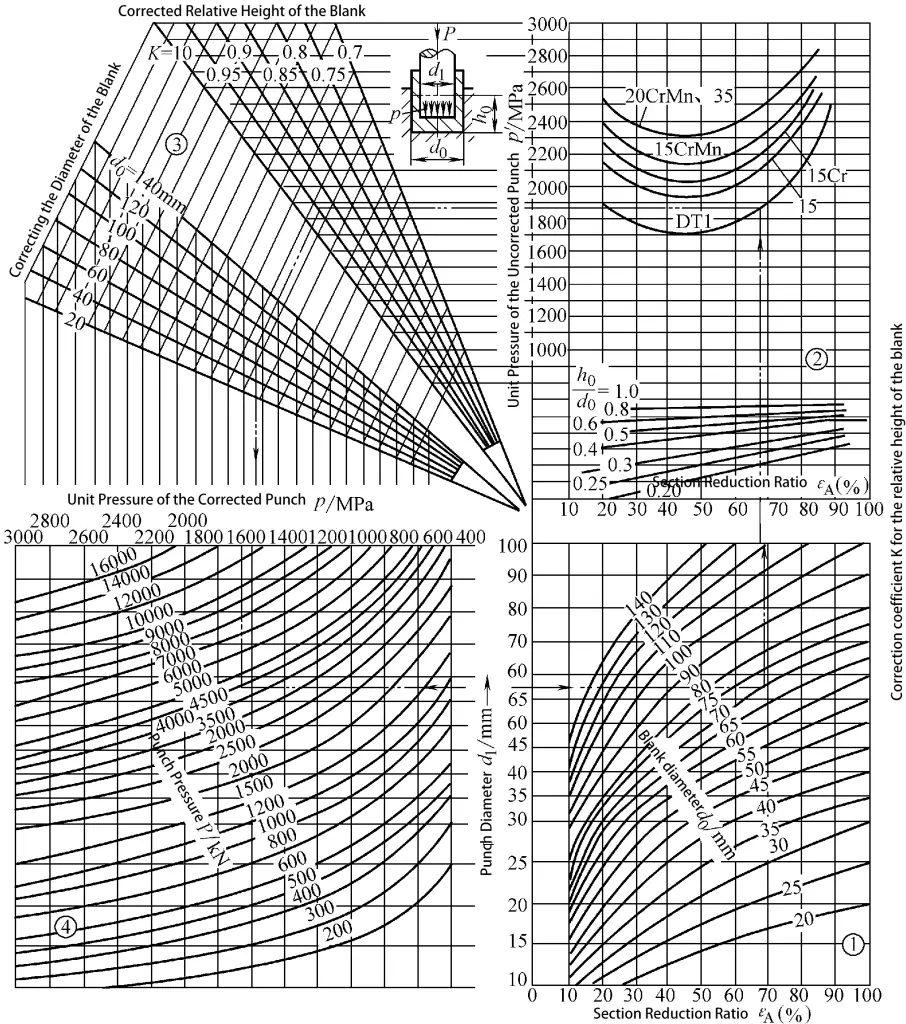
Katı ekstrüzyon için birim ekstrüzyon kuvvetinin grafiksel hesaplaması Şekil 3-9'da gösterilmektedir. İçi boş ekstrüzyon için birim ekstrüzyon kuvvetinin grafiksel hesaplaması Şekil 3-10'da gösterilmektedir.
Tablo 3-13 Ekstrüzyon Sırasında Birim Ekstrüzyon Kuvvetinin Yaklaşık Değeri
| Malzeme | Deformasyon Durumu | |||||
| Doğrudan Ekstrüzyon | Dolaylı Ekstrüzyon | Kapalı Kalıp Şekillendirme | ||||
| Kesitsel Azaltma Oranı εA (%) | Birim Ekstrüzyon Kuvveti ρ/MPa | Kesitsel Azaltma Oranı εA (%) | Birim Ekstrüzyon Kuvveti ρ/MPa | Kesitsel Azaltma Oranı εA (%) | Birim Ekstrüzyon Kuvveti ρ/MPa | |
| Saf Alüminyum | 97 ~ 99 | 600 ~ 800 | 97 ~99 | ≈800 | 30 ~ 50 | / |
| Alüminyum Alaşım | 92 ~ 95 | 800 ~ 1000 | 75 ~82 | 800 ~ 1200 | 30 ~ 50 | 1000 ~ 1600 |
| Pirinç | 75 ~87 | 800 ~ 1200 | 75 ~ 78 | 800 ~ 1200 | 30 ~ 50 | 1000 ~ 1600 |
| 10 Çelik | 50 ~ 80 | 1400 ~ 2000 | 40 ~75 | 1600 ~ 2200 | 30 ~ 50 | 1000 ~ 1600 |
| 30 Çelik | 50 ~ 70 | 1600 ~ 2500 | 40 ~ 70 | 1800 ~ 2500 | 30 ~ 50 | 1600 ~ 2000 |
| 50 Çelik | 40 ~ 60 | 2000 ~ 2500 | 30 ~ 60 | 2000 ~ 2500 | 30 ~ 50 | 1800 ~ 2500 |
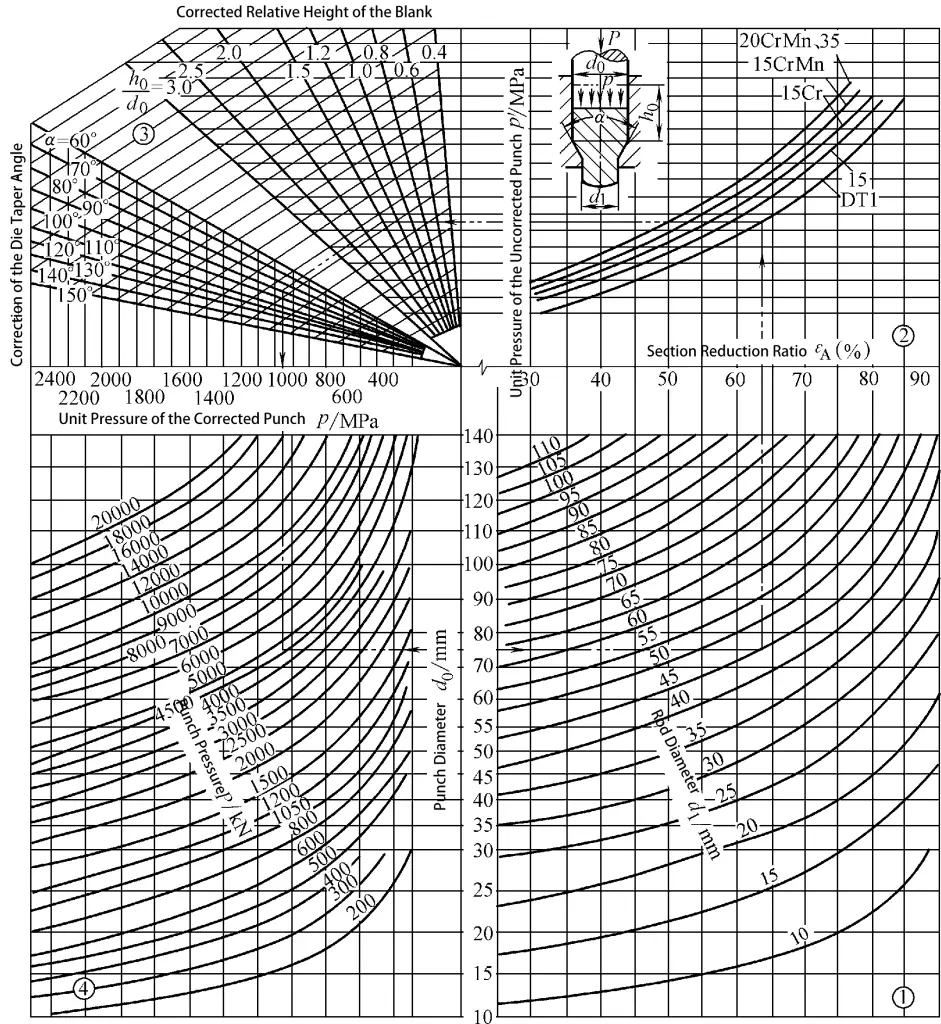
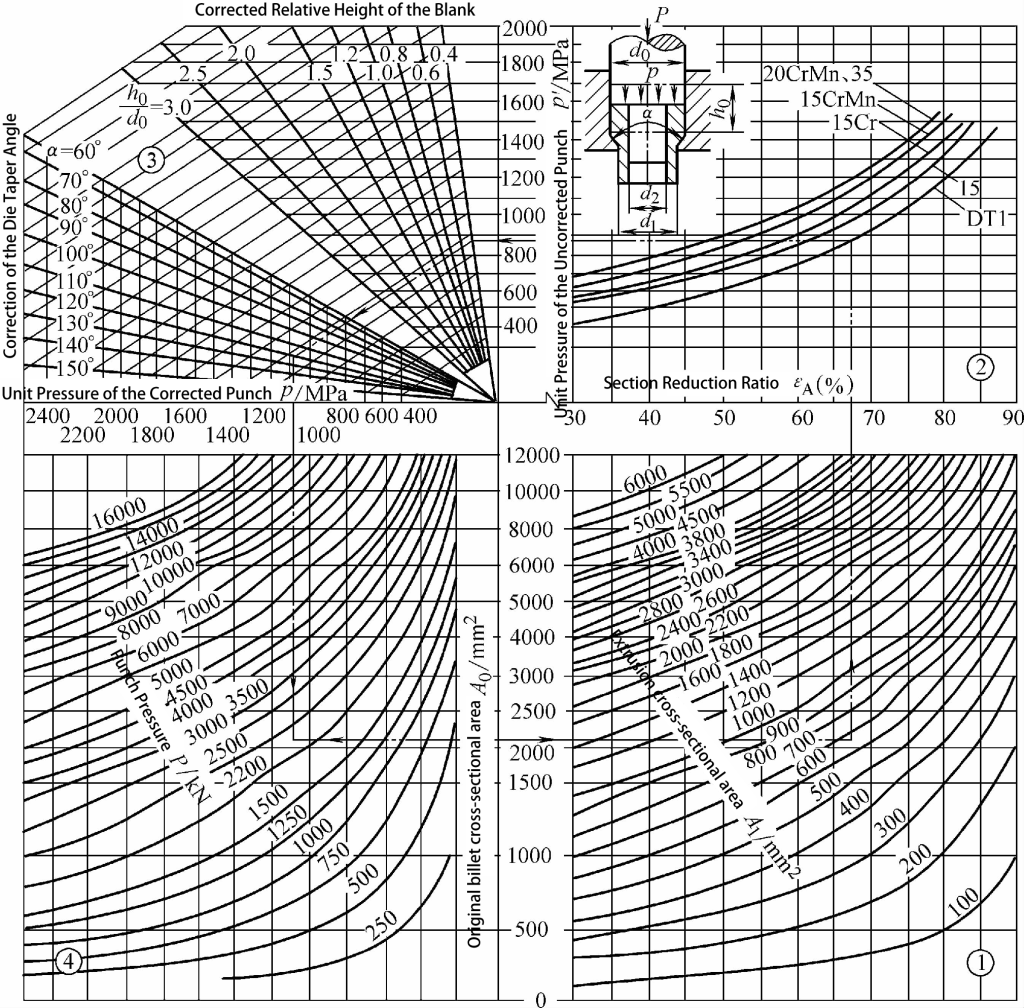
Grafiksel Yöntem: Gerekli birim ekstrüzyon kuvvetini ve toplam ekstrüzyon kuvvetini bulmak için şekilde oklarla gösterilen yönde ilerleyin.
Örneğin, katı bir parçanın doğrudan ekstrüzyonu sırasında birim ve toplam ekstrüzyon kuvvetini bulmak için: Kütük çapının d olduğunu varsayalım1 75 mm, ekstrüzyon çubuğu çapı d0 45 mm, kütük yüksekliği h 110 mm ve kalıp koni açısı α 90 derecedir. Malzeme saf demir DT1'dir. Şekil 3-9'a bakarak, p birim ekstrüzyon kuvvetinin 1050MPa ve toplam P ekstrüzyon kuvvetinin 4600kN olduğunu buluyoruz.
Benzer şekilde, içi boş bir parçanın doğrudan ekstrüzyonu sırasında birim ve toplam ekstrüzyon kuvvetini bulmak için: Kütük çapının d0 95 mm olduğunu, ekstrüde parçanın dış çapının d1 85 mm, iç çap d2 80 mm, kütük yüksekliği h0 50 mm ve kalıp koni açısı α 120 derecedir. Malzeme saf demir DT1'dir. Şekil 3-10'a bakarak, p birim ekstrüzyon kuvvetinin 1080MPa ve toplam P ekstrüzyon kuvvetinin 2230kN olduğunu buluyoruz.
(2) Geriye Doğru Ekstrüzyonda Çelik Malzeme için Birim Ekstrüzyon Kuvvetinin Grafiksel Hesaplanması
Çelik fincan şeklindeki parçaların geriye doğru ekstrüzyonu için birim ekstrüzyon kuvveti ve toplam ekstrüzyon kuvveti Şekil 3-11'de gösterildiği gibi grafiksel olarak hesaplanabilir.
Grafik nasıl kullanılır? Gerekli birim ekstrüzyon kuvvetini ve toplam ekstrüzyon kuvvetini bulmak için resimdeki ok yönünü takip edin.
Örneğin, bir kütük çapı verildiğinde (d0) 70 mm, zımba çapı (d1) 58 mm, kütük yüksekliği (h0) ve saf demirden (DT1) oluşan bir malzeme için, Şekil 3-11'den birim ekstrüzyon kuvvetinin (p) 1660 MPa ve toplam ekstrüzyon kuvvetinin (P) 4400 kN olduğunu belirleyebiliriz.
Çizelgede metal malzemelerin sadece bir kısmının listelendiği unutulmamalıdır. Listelenmeyenler için metaller'yi hesaplamak için grafikte benzer karbon içeriğine sahip bir metal bulabilir, ardından çekme mukavemetlerinin oranını (Rm) tavlamadan sonra iki metalin ekstrüzyon kuvvetini elde etmek için çizelgede bulunan ekstrüzyon kuvveti ile ekstrüde edilmiş malzemenin ekstrüzyon kuvveti.
Örneğin, ileri ekstrüzyonda GCr15 rulman çeliğinin birim ekstrüzyon kuvvetini bulmak için, GCr15 ve 35 çeliğinin karbon içeriğinin benzer olmadığını ve tavlamadan sonra GCr15'in Rm'sinin 650~750 MPa olduğunu, tavlamadan sonra 35 çeliğinin Rm'sinin ise 530~550 MPa olduğunu biliyoruz.
Şekil 3-9'dan, ilgili boyuttaki 35 çelik parça için birim ekstrüzyon kuvveti (p) 2000 MPa'dır, bu nedenle GCr15 için birim ekstrüzyon kuvveti yaklaşık 2000 x (750/550) MPa, yani yaklaşık 3000 MPa'dır.
(3) Demir Dışı Metallerin Birim Ekstrüzyon Kuvveti için Grafik Hesaplama Yöntemi
Katı ve içi boş parçaların doğrudan ekstrüzyonu ve demir dışı metallerde fincan şeklindeki parçaların ters ekstrüzyonu için birim ekstrüzyon kuvveti grafikleri Şekil 3-12 ila 3-14'te gösterilmiştir. Bu grafiklerde, σ malzemenin ortalama deformasyon direncini temsil eder; deformasyon verimliliği boşluk yüksekliği ve kesit küçültme oranına göre değişir.
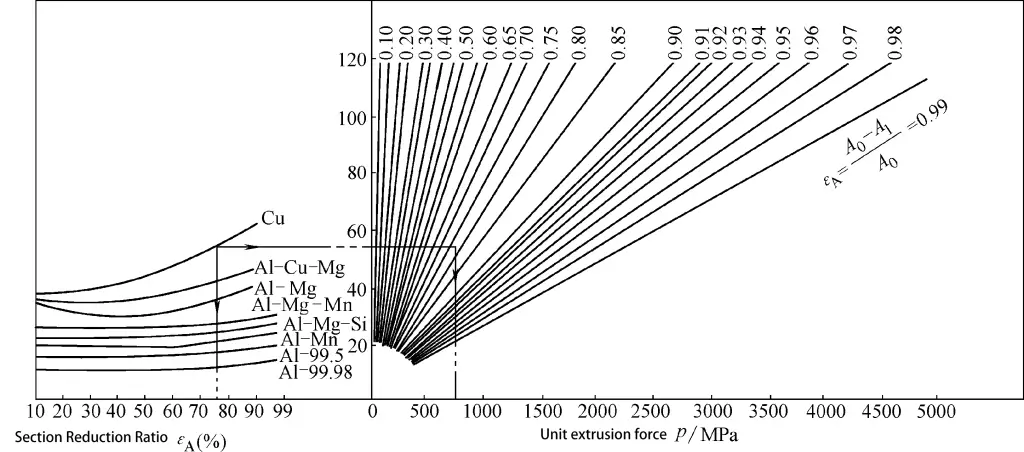
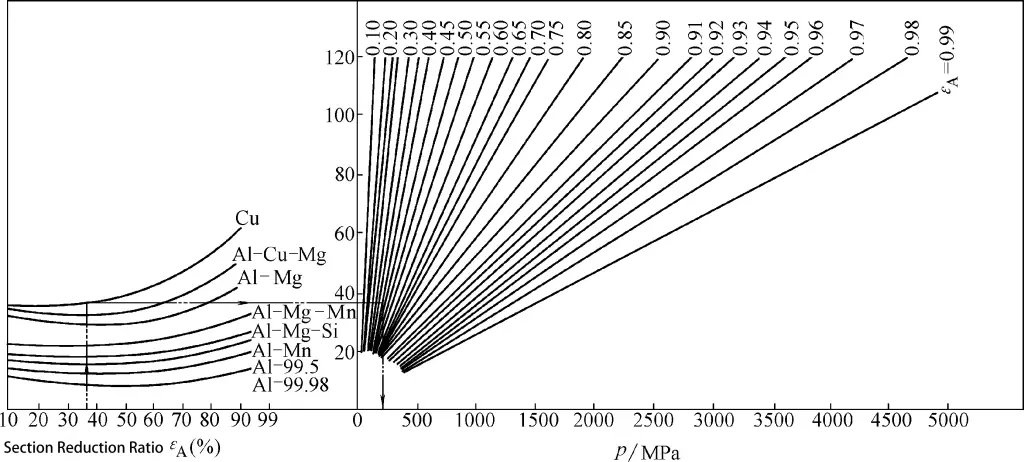
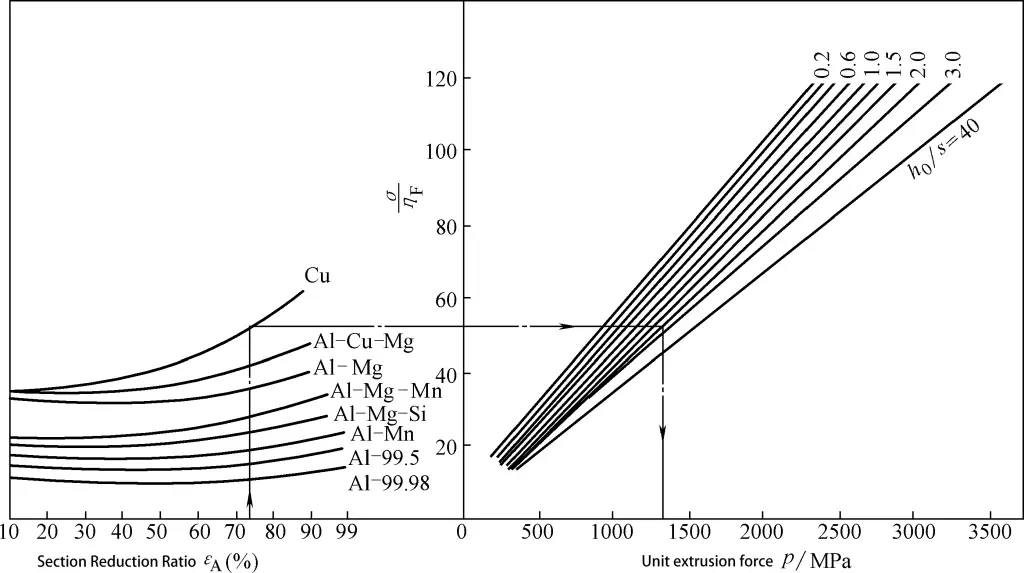
Grafik Okuma Yöntemi: Gerekli birim ekstrüzyon kuvveti, grafikteki okların gösterdiği yön takip edilerek elde edilebilir.
Örneğin, bakır malzemeden doğrudan ekstrüde edilen katı bir parçanın birim ekstrüzyon kuvvetini hesaplamak için. Boş bir çap verildiğinde (d0) 50 mm ve ekstrüde çubuk çapı (d1) 24 mm olduğunda, birim ekstrüzyon kuvvetinin (p) 760MPa olduğunu bulmak için Şekil 3-12'ye bakabiliriz.
(4) Çelik Malzemenin Bilinen Vickers Sertliğine Dayalı Birim Ekstrüzyon Kuvveti için Grafik Hesaplama Yöntemi
Metal malzemenin türü bir faktör olarak dikkate alınarak yapılan grafiklerin tüm malzemeleri listelemesi mümkün değildir. Listelenmemiş malzemeler için karbon içeriklerine göre dönüştürme yapmak uygun değildir. Şekil 3-15 ve 3-16, çelik malzemelerin tavlanmasından sonra Vickers Sertliği (HV) parametresi ile oluşturulan grafikleri göstermektedir. Bu grafiklerdeki sertlik değerleri değiştikçe, ortaya çıkan birim ekstrüzyon kuvveti de buna göre değişmelidir.
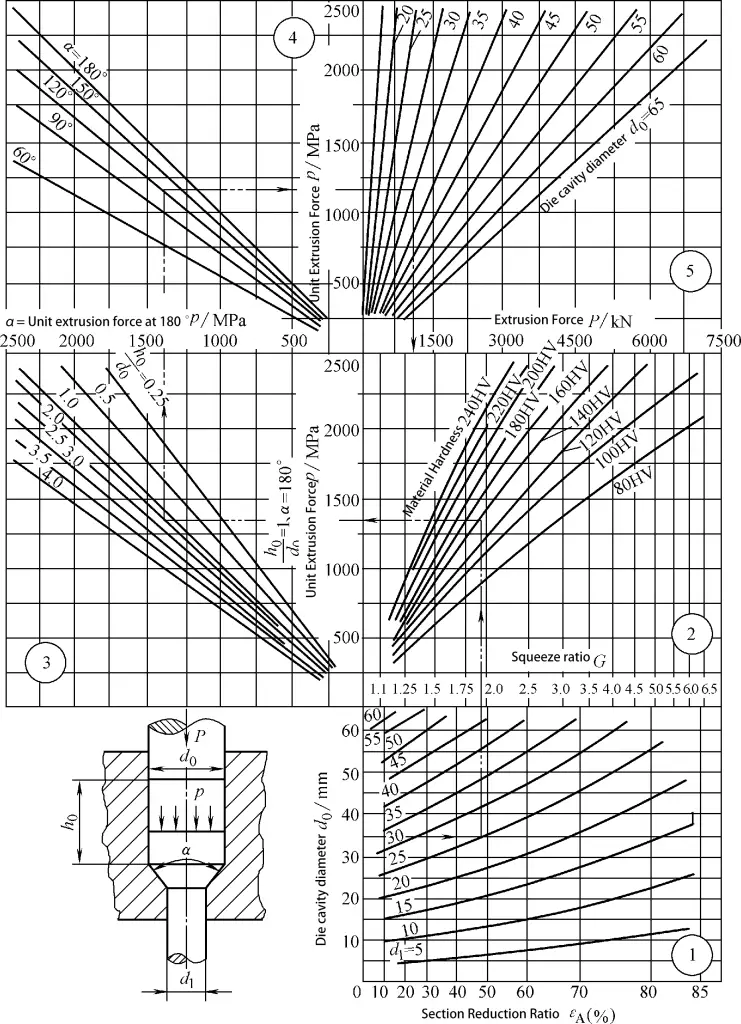
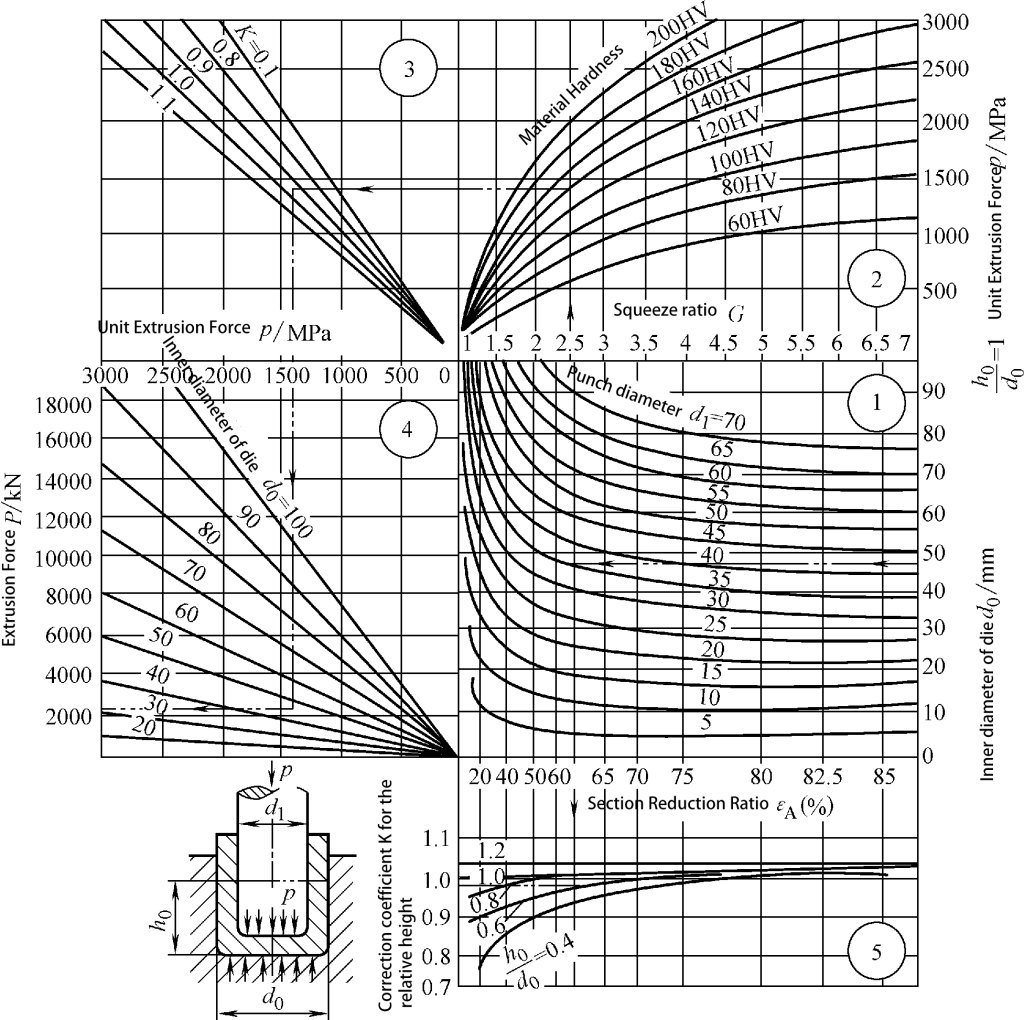
Grafik Referans Yöntemi: Gerekli birim ekstrüzyon basıncını ve toplam ekstrüzyon basıncını bulmak için tablodaki okların yönünü izleyin.
Örneğin, katı bir parçanın doğrudan ekstrüzyonu için birim ekstrüzyon basıncını ve toplam ekstrüzyon basıncını bulmak için.
Boş çapın d olduğu göz önüne alındığında0 35 mm, yükseklik h0 35 mm, ekstrüde parça çapı d1 25 mm'dir ve malzemenin Vickers sertliği 140HV'dir, kalıp açısı α 120°'dir; Şekil 3-15'e bakarak, birim ekstrüzyon basıncı p 1220MPa ve toplam ekstrüzyon basıncı P 1180kN olarak bulunabilir.
Grafiksel Analiz Yöntemi
Basit çubuk şekilli veya fincan şekilli parçaların ekstrüzyon basıncı, mevcut ampirik formüller veya çizelgeler kullanılarak tahmin edilebilir. Ancak, karmaşık şekilli iş parçalarının ekstrüzyon basıncı için kapsamlı bir hesaplama yöntemi veya pratik ve güvenilir sütun çizelgeleri yoktur.
Örneğin, doğrudan ekstrüzyon altında Şekil 3-17'de gösterilen parçanın ekstrüzyon basıncını hesaplamak için doğrudan benimsenebilecek hazır formüller veya çizelgeler yoktur. Bu nedenle, Şekil 3-18'de gösterildiği gibi, hesaplama için özel olarak analiz etmek ve basit bir fincan şeklindeki parçaya ayrıştırmak gerekir.
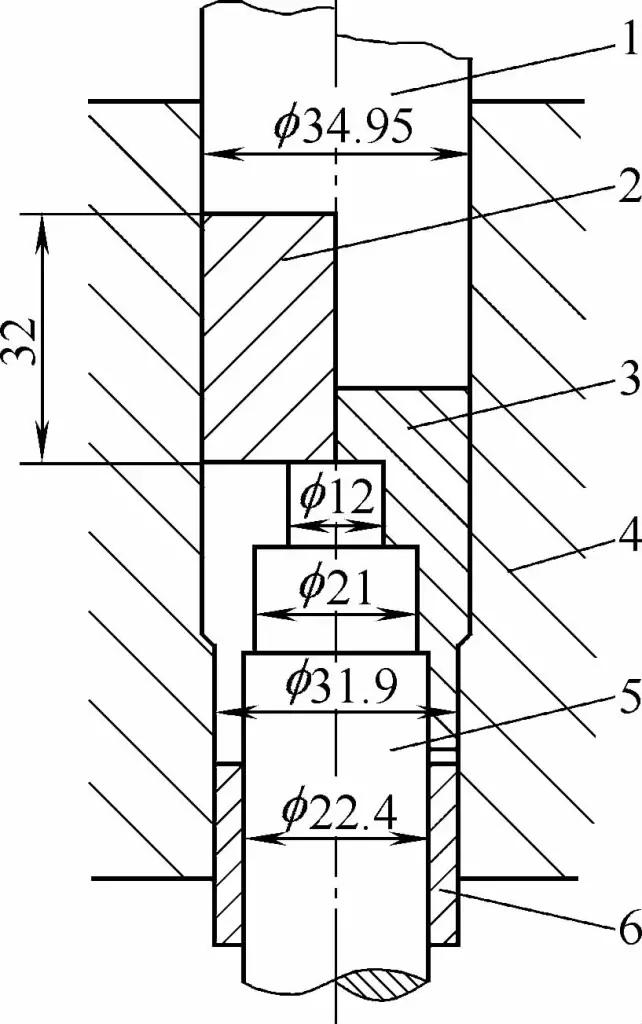
1-Punch
2-Boş
3-Ekstrüde Parça
4-Die
5-Alt Yumruk
6-Yuvarlak Ejektör Kovanı
Hesaplama yapılırken, Şekil 3-18a'da gösterilen ekstrüde parçanın dış adımı 4 ilk olarak düz duvarlı silindirik bir parçaya basitleştirilir (bkz. Şekil 3-18b), bu ilk şekil basitleştirmesidir. Delik 2 ve 3'ün boyutları nispeten benzer olduğundan, iki delik tek bir büyük delik olarak düşünülebilir ve Şekil 3-18c'de gösterilen şekle dönüşür, bu ikinci şekil sadeleştirmesidir.
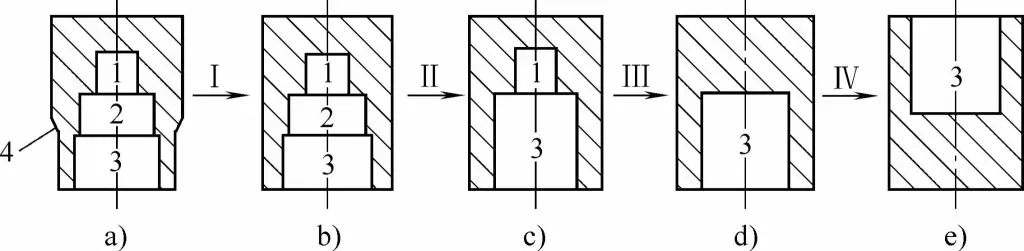
1, 2, 3 - Delikler; 4 - Adım
Küçük delik 1 de ayrı olarak ele alınırsa, üçüncü basitleştirmeden sonraki şekil basitleştirilmiş doğrudan ekstrüzyon fincan şeklindeki bir parçadır (bkz. Şekil 3-18d). Alternatif olarak, hesaplamalar ters ekstrüzyon altında fincan şeklinde bir parça ile başlayabilir (bkz. Şekil 3-18e).
Bu noktada, son basitleştirme işlemi tamamlanır. Bu şekilde, belirli bir analiz ve basitleştirmeden sonra, iç ve dış basamak benzeri bir şekle sahip karmaşık bir parça, çok daha basit ve kolay olan gerekli ekstrüzyon basıncını hesaplamak için tipik bir ters ekstrüzyon kabı şeklindeki parça olarak ele alınabilir.
Hesaplamada, son basitleştirilmiş şekilden başlamalı ve geriye doğru ilerlemeliyiz. Hesaplama işlemi sırasında, her bir şeklin ekstrüzyon kuvveti üzerindeki etkisini göz önünde bulundurmalı ve böylece gerekli ekstrüzyon kuvvetini kademeli olarak belirlemeliyiz. Ters ekstrüde edilmiş fincan şeklindeki parçanın (bkz. Şekil 3-18e) ekstrüzyon kuvveti P olarak gösterilir ve değeri burada detaylandırmayacağımız mevcut formüller ve çizelgelerden elde edilebilir.
Kupa şeklindeki parça doğrudan ekstrüzyon yöntemi kullanılarak işlenirse (bkz. Şekil 3-18d), ekstrüzyon kuvveti Şekil 3-19'da gösterildiği gibi 15% ila 20% daha yüksek olacaktır. Dolayısıyla, bu noktadaki ekstrüzyon kuvveti 1,2P olacaktır. Genel olarak, kademeli bir deliğin varlığı ekstrüzyon kuvvetini Şekil 3-20'de görüldüğü gibi yaklaşık 20% artıracaktır. Bu nedenle, Şekil 3-18c'de gösterilen şekil için ekstrüzyon kuvveti 1,44P (1,2P x 1,2) olacaktır.
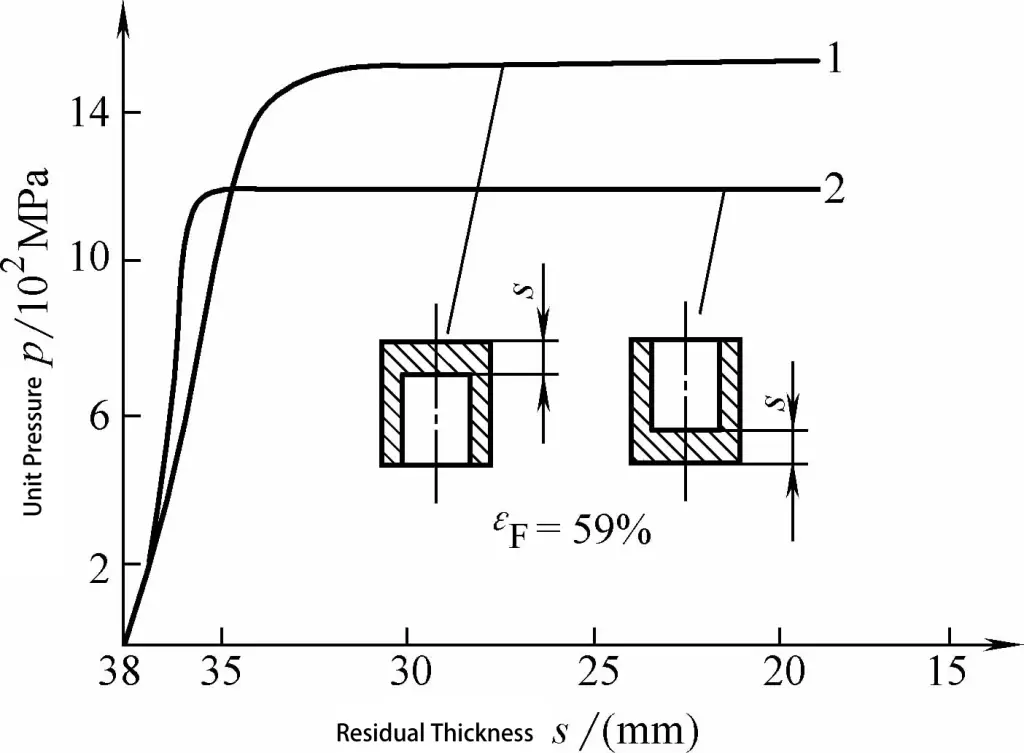
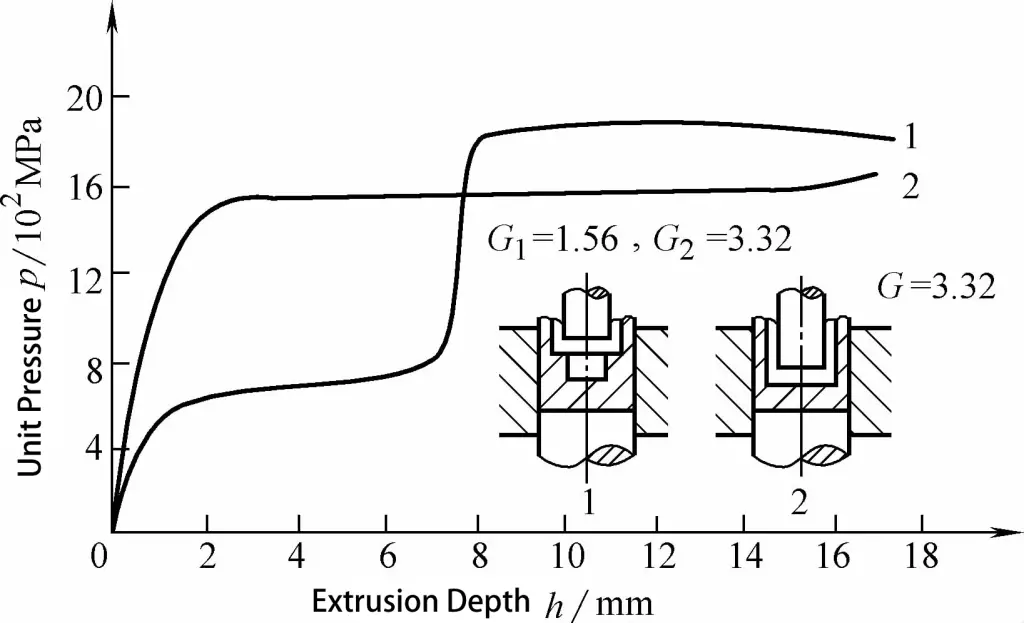
1. Kademeli Delikler ile Dolaylı Ekstrüzyon
2. Düz Delikli Dolaylı Ekstrüzyon
Basamaklı deliklerin (delik 2 ve 3) boyutları çok az değiştiğinden, bunların etkisi ihmal edilebilir. Bu nedenle Şekil 3-18b'de gösterilen şekil için ekstrüzyon kuvveti 1.44P olarak kalır. Dış basamak 4'ün etkisi (bkz. Şekil 3-18a) ekstrüzyon kuvvetinde 10%'lik bir artış olarak kabul edilir, bu nedenle Şekil 3-18a'da gösterilen şekil için ekstrüzyon kuvveti 1,58P (1,44P x 1,1) olur.
Bu parçanın boş boyutunun 34,94 mm x 32 mm ve deformasyon derecesinin 40% (Şekil 3-18e) olduğu varsayıldığında, genel grafikten elde edilen ekstrüzyon kuvveti yaklaşık 800kN'dir. Bu nedenle, Şekil 3-17'de gösterilen doğrudan ekstrüzyon kademeli parça için gerekli ekstrüzyon kuvveti 1264kN'dir (800kN x 1.58).
Bu nedenle, karmaşık şekilli parçaların ekstrüzyon kuvvetini hesaplamak için formül şöyledir:
P = P1C1C2 (3-10)
Nerede?
- P1 basit çubuk şeklindeki veya fincan şeklindeki parçanın ekstrüzyon kuvvetidir (N);
- C1 şeklin karmaşıklık faktörüdür;
- C2 deformasyon yöntemi etki faktörüdür.
Karmaşıklık faktörü, esas olarak kademeli şeklin ekstrüzyon kuvveti üzerindeki etkisi göz önünde bulundurularak ekstrüzyon parçası şeklinin karmaşıklığı ile belirlenir. İlgili tasarım malzemelerine ve deneysel eğrilere dayanarak yaklaşık olarak seçilebilir. Karmaşıklık faktörü C1'in tam seçimi tasarımcının deneyimiyle yakından ilgilidir.
Deformasyon yöntemi etki faktörü esas olarak doğrudan ekstrüzyon, ters ekstrüzyon ve ikisinin kombinasyonu arasındaki deformasyon kuvveti farkını dikkate alır. Genellikle 20% artış civarında, yani C2 ≈ 1,2 olacak şekilde seçilir.
Bu nedenle, karmaşık şekilli parçaların ekstrüzyon kuvvetini hesaplamak için grafiksel analiz süreci:
1) Karmaşık şekilli ekstrüzyon parçasını, hesaplama için başlangıç şekli olarak hizmet eden basit bir çubuk şekilli veya fincan şekilli parçaya kademeli olarak basitleştirin.
2) Her bir vücut arasındaki farklılıkları analiz edin ve bunları bağımsız faktörler olarak değerlendirin.
3) Grafik ayrıştırma ve basitleştirme sürecini kapsamlı bir şekilde analiz edin ve bunu ekstrüzyon parçasının gerçek soğuk ekstrüzyon kuvvetini hesaplamak için teknolojik bir model olarak kullanın.
Ekstrüzyon kuvvetini çözmek için grafik analiz kullanmak basit, pratik ve etkili bir mühendislik hesaplama yöntemidir. Bu yöntemin tahmin doğruluğu gereksinimleri karşılamak için yeterlidir.
Bileşik ekstrüzyonun ekstrüzyon kuvveti için hesaplama yöntemi şöyledir: Bileşik ekstrüzyon için gerekli ekstrüzyon kuvveti, Şekil 3-21 ve 3-22'de görüldüğü gibi, daha küçük bir deformasyon derecesine sahip tek yönlü ekstrüzyon için gereken değere eşit veya biraz daha düşüktür. Bu, bileşik ekstrüzyon için basıncı hesaplarken, sadece daha küçük deformasyon derecesine sahip yönün ekstrüzyon kuvveti değerini çözmemiz gerektiği anlamına gelir.
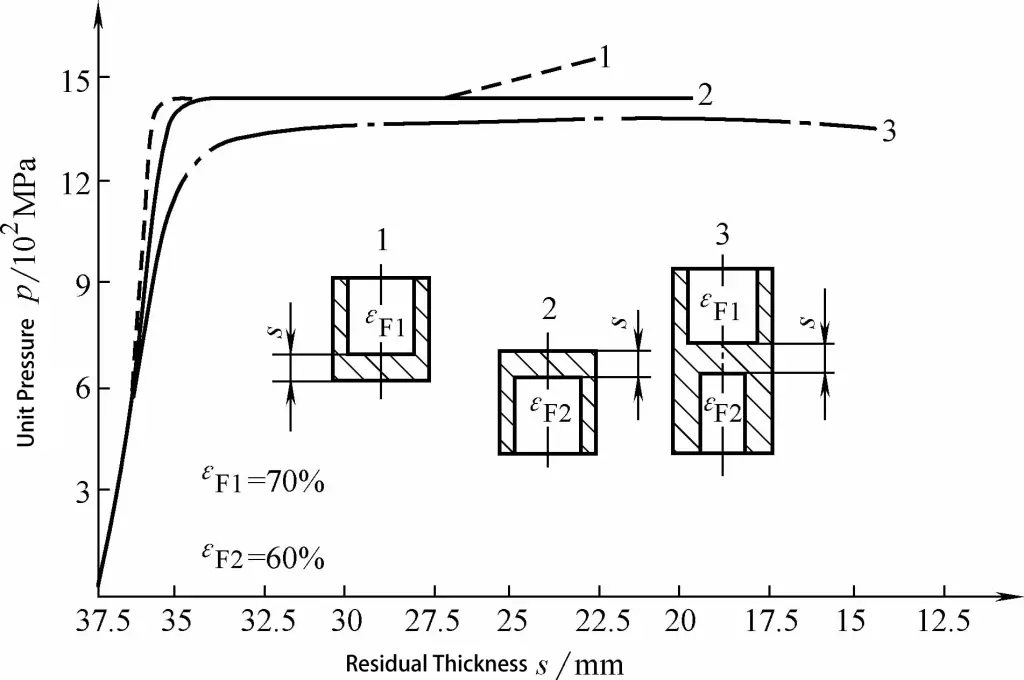
1. Dolaylı Ekstrüzyon
2. Doğrudan Ekstrüzyon
3. Kompozit Ekstrüzyon
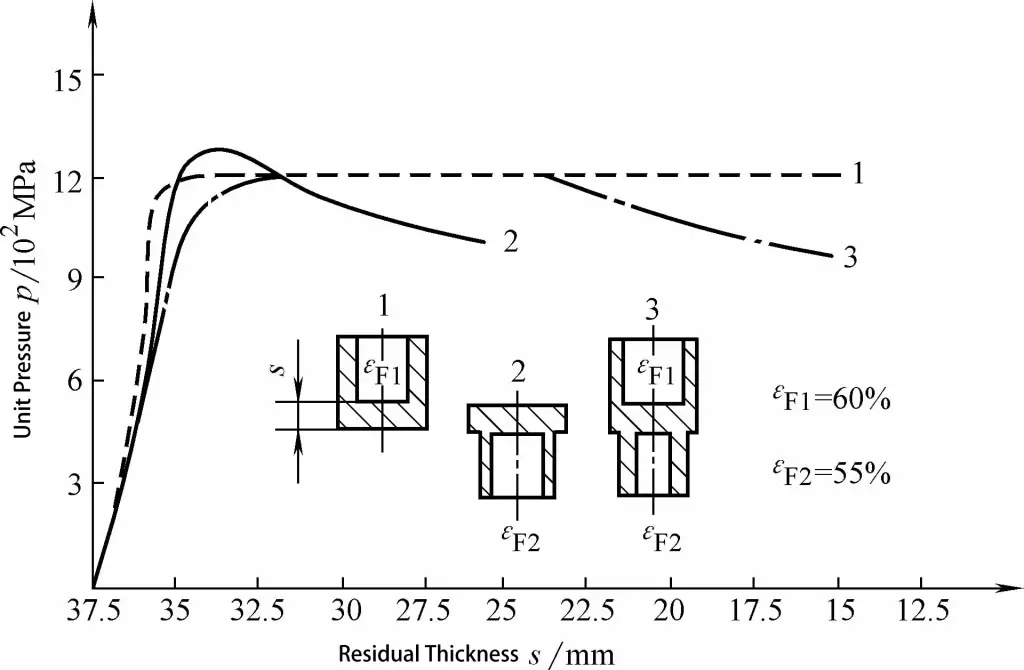
1. Dolaylı Ekstrüzyon
2. Doğrudan Ekstrüzyon
3. Kompozit Ekstrüzyon
Kompozit ekstrüzyon belirli bir yönde boyutu kısıtlamadığında, yani kalıp her iki uçta açıkken metal her iki yönde serbestçe aktığında, basınç şu şekilde tanımlanır:
Pcomp=Pdoğrudan (Pdoğrudan<Pdolaylı) (3-11)
Pcomp=Pdolaylı(Pdolaylı<Pdoğrudan (3-12)
Nerede?
- Pdoğrudan aynı kütük boyutu ve deformasyon derecesi (N) ile tek yönlü dolaylı ekstrüzyon için gereken basınçtır.
- Pdolaylı aynı kütük boyutu ve deformasyon derecesi (N) ile tek yönlü doğrudan ekstrüzyon için gereken basınçtır.
Kompozit ekstrüzyon belirli bir yönde boyutu kısıtladığında, yani ekstrüzyon işlemi sona ermek üzereyken bir uçta kapatma ekstrüzyonu gerektiğinde, basınç şu şekilde tanımlanır:
- Pcomp=Pdoğrudan boyut dolaylı ekstrüzyon yönünde sınırlandırılmışsa (3-13)
- Pcomp=Pdolaylı boyut doğrudan ekstrüzyon yönünde sınırlandırılmışsa (3-14)