Au cours du processus de création du dessin de développement du composant en tôle, il est également nécessaire de prendre en compte l'impact de l'épaisseur du matériau de transformation, c'est-à-dire de procéder aux ajustements appropriés de l'épaisseur de la tôle.
En règle générale, pour les tôles d'une épaisseur inférieure à 3 mm, aucun ajustement de l'épaisseur de la tôle n'est nécessaire. Elle peut être calculée en fonction du diamètre central de la tôle ou en fonction des lignes de coupe des surfaces intérieures et extérieures. Les dimensions après formage se situent dans la plage de déviation autorisée. Lorsque l'épaisseur de la tôle est supérieure à 3 mm, elle doit être calculée en fonction du diamètre central de la tôle. Pour faciliter la description, les calculs pour les matériaux développés suivants se réfèrent au diamètre central du matériau en feuille.
1. Calcul du développement des coques cylindriques
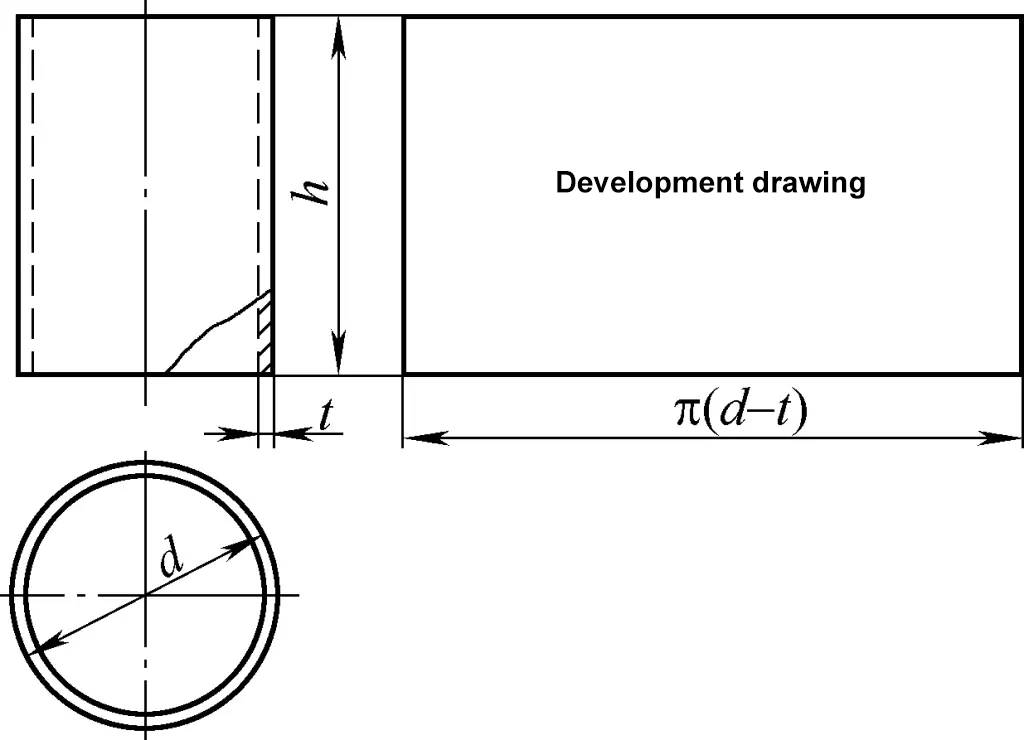
L'enveloppe cylindrique appartient à la surface cylindrique et son plan de développement est un rectangle. Un côté du rectangle est égal à la circonférence du cylindre π(d-t), et l'autre côté est la hauteur h du cylindre, comme le montre la figure 1. Dans la figure, d est le diamètre extérieur du cylindre et t l'épaisseur de la plaque.
2. Calcul du développement des cônes circulaires droits
Le plan de développement du cône circulaire droit est un arc de cercle. La formule de calcul pour le dessin de développement du cône circulaire droit illustré à la figure 2 est la suivante :
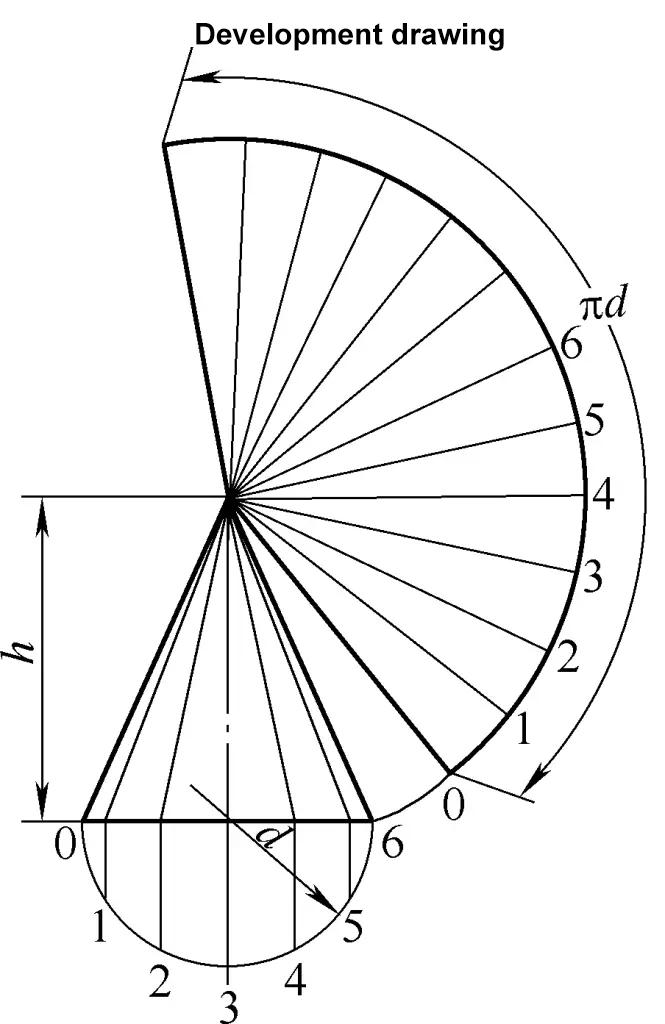
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
Dans la formule
- R - Rayon de l'arc sectoriel (mm) ;
- α - Angle du secteur (°) ;
- L - Longueur de la corde de l'arc sectoriel (mm).
3. Calcul du développement des cônes circulaires droits tronqués
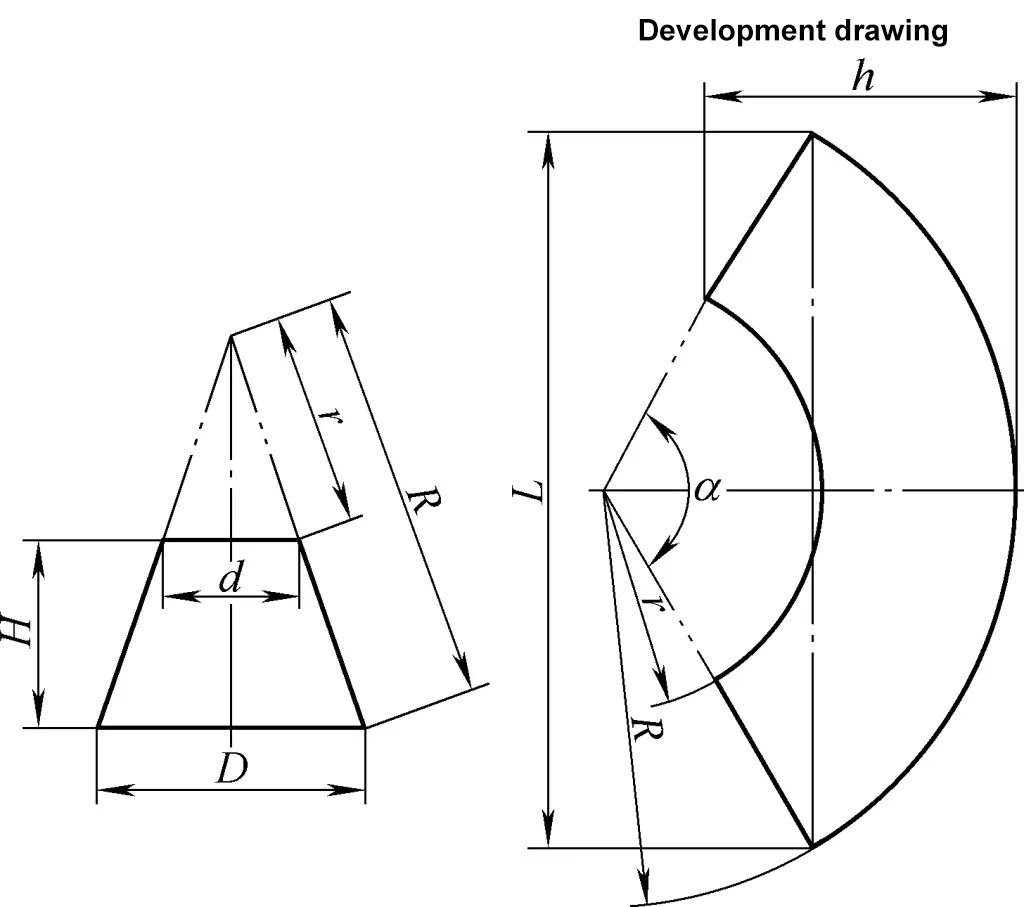
Le plan de développement du cône circulaire tronqué à droite est un arc de secteur concentrique. La formule de calcul pour le dessin de développement du cône circulaire tronqué droit illustré à la figure 3 est la suivante :
R=√{(D/2)2+[DH/(D-d)]2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
Lorsque α>180°, h=R+rsin[(α-180)/2]
Pour connaître la signification des symboles de la formule, reportez-vous à la figure 3.
4. Calcul du développement des cônes circulaires droits obliques
Le plan de développement du cône circulaire oblique droit est un arc de secteur irrégulier. La formule de calcul pour le dessin de développement du cône circulaire oblique droit illustré à la figure 4 est la suivante :
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[(A-D/2cosαn)2+(D/2)2péché2αn+H2]
yn=fn(1-h/H)
m=Dsin(180°/n )
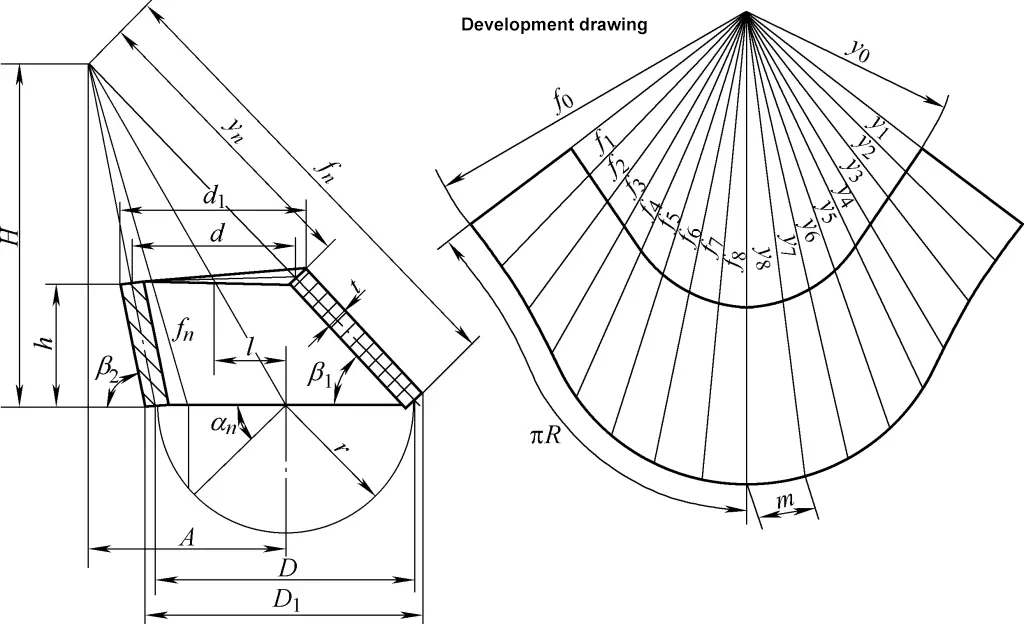
Dans la formule
- D1, d1 - Diamètres extérieurs de la grande et de la petite extrémité (mm) ;
- D, d - Diamètres centraux de la grande et de la petite extrémité (mm) ;
- h - Hauteur centrale (mm) ;
- l - Distance excentrique (mm) ;
- n - Nombre de divisions autour de la circonférence ; plus le nombre de divisions est élevé, plus le calcul est complexe, mais plus le dessin est précis. En général, le nombre de divisions peut être référencé dans le tableau 1 ;
- fn, yn - Longueurs des lignes obliques du cône circulaire droit oblique (mm).
Tableau 1 Nombre de divisions pour les développements de la tôle
| Rayon de la pièce développée/mm | Nombre de divisions |
| Dans la limite de 50 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| Plus de 2000 | 96 |
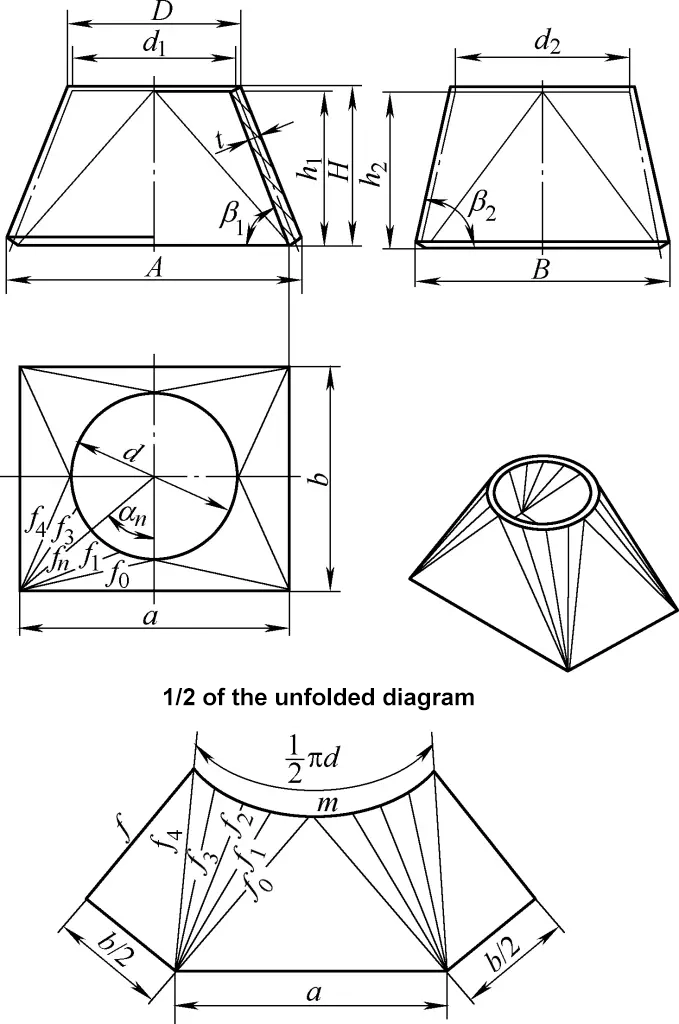
5. Calcul du développement du conduit de transition orthoconique rectangulaire à rond
Le conduit de transition orthoconique rectangulaire à rond illustré à la figure 5 se compose de quatre surfaces coniques droites obliques égales et de quatre plans triangulaires symétriques. La formule de calcul pour son plan de développement est la suivante
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(quand 0<α<90°)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(quand α=90°)
f=1/2√[(a-d)2+4h12]
m=πd/n
Pour la signification des symboles de la formule, voir la figure 5, et n est le nombre de divisions autour de la circonférence. En règle générale, le nombre de divisions indiqué dans le tableau 1 permet de répondre aux exigences de calcul.