Pour les pièces de pliage de tôle, le calcul de la taille de l'ébauche est une condition préalable à la formulation du plan de processus de pliage. Différents techniciens peuvent sélectionner différents facteurs de surépaisseur de pliage dans leurs documents de processus, et la précision de la taille de l'ébauche a un impact direct sur la précision dimensionnelle et la qualité du produit des pièces pliées.
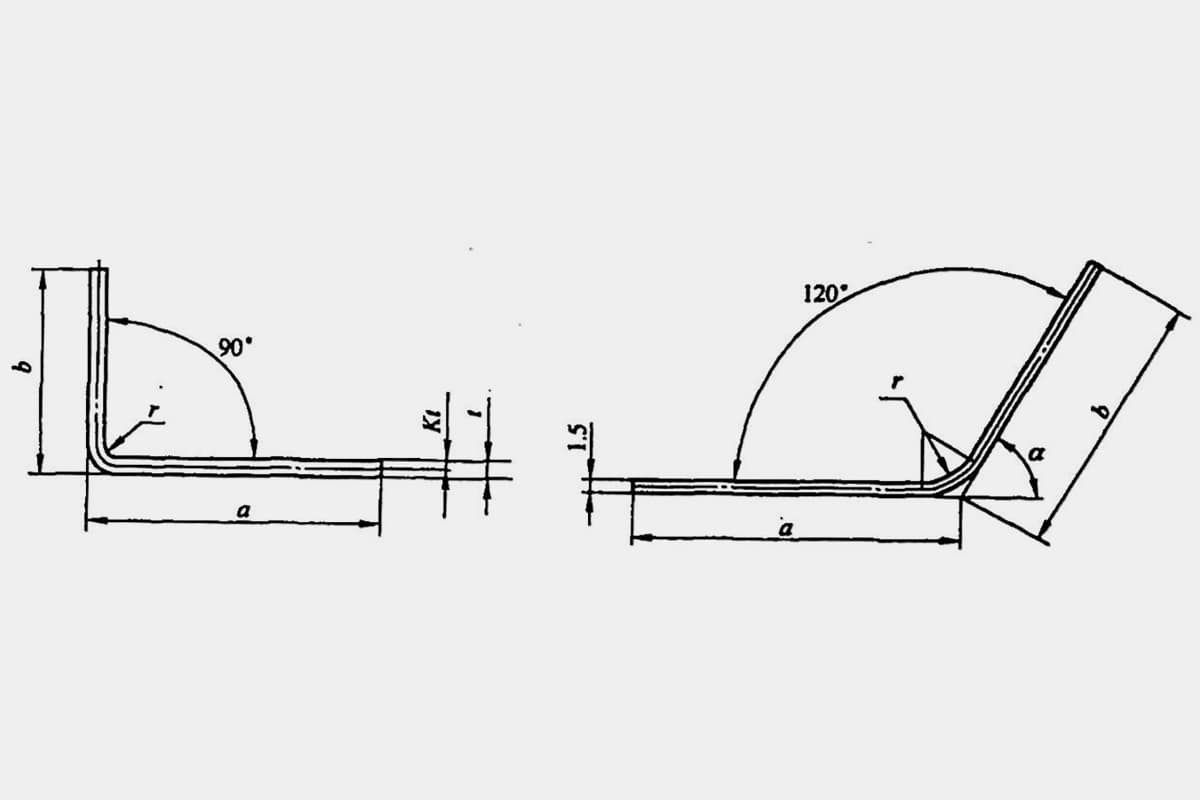
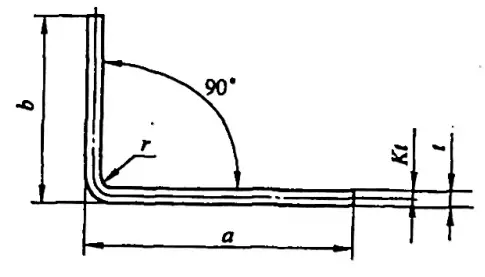
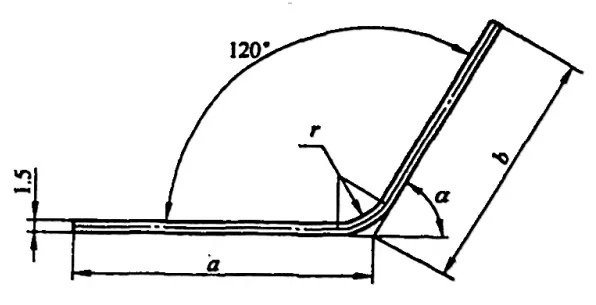
Parfois, des calculs imprécis peuvent même entraîner des déchets. La longueur dépliée L d'une pièce de flexion simple typique (voir figure 5-1) est L = a + b - y (où y est la déduction de flexion, également connue sous le nom de valeur de correction pour la pièce R).
Toutefois, dans divers manuels et documents, la déduction de la flexion pour φ=90° peut être obtenue directement, alors que pour les courbes à 90°, comme celles de la figure 5-2, les techniciens doivent la calculer sur la base d'un facteur d'expérience (facteur K).
Lecture connexe : L'art du dépliage de la tôle expliqué
1. Principe de calcul de la dimension dépliée des plis de tôle
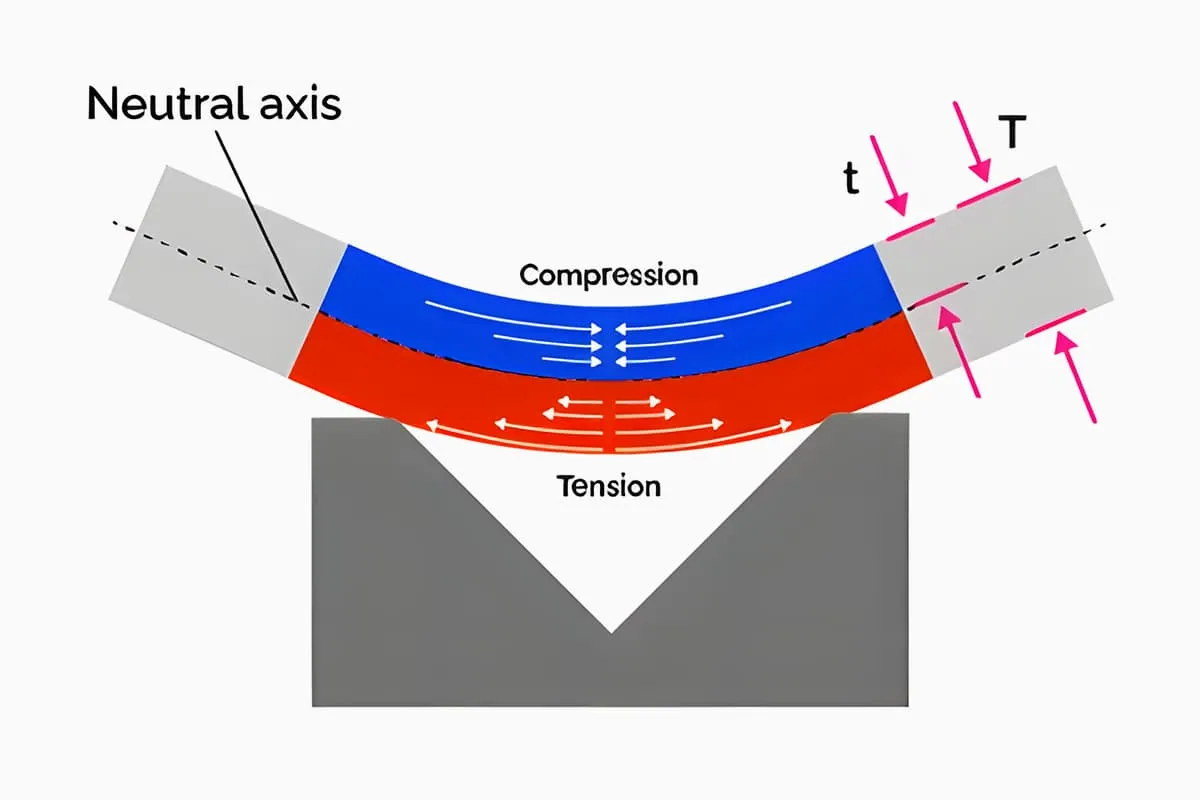
La dimension dépliée d'une ébauche pliée est déterminée sur la base du principe selon lequel la longueur de la couche neutre reste inchangée avant et après le pliage. Lorsque la tôle est pliée, les fibres de la couche extérieure de la section du flan sont étirées et les fibres de la couche intérieure sont comprimées.
L'étirement des fibres de la couche extérieure diminue progressivement de l'extérieur vers l'intérieur, et la compression des fibres de la couche intérieure diminue également progressivement de l'intérieur vers l'extérieur.
Lorsque les fibres passent de l'étirement à la compression ou de la compression à l'étirement, il doit y avoir une couche de fibres où la contrainte et la déformation sont nulles et dont la longueur reste inchangée avant et après la flexion.
Cette couche est ce que nous définissons comme la couche neutre. Par conséquent, la clé du calcul de la dimension dépliée de l'ébauche pliée consiste à déterminer la position de la couche neutre. La position de la couche neutre est déterminée à condition que le volume de la pièce pliée et celui de l'ébauche soient égaux avant et après la déformation plastique.
2. Détermination du rayon de courbure ρ de la couche neutre
En théorie, en raison de la déformation inégale dans le sens de l'épaisseur de la pièce pliée, la couche neutre est une surface parabolique, mais pour les besoins du calcul, elle est généralement considérée comme une surface en arc de cercle. Lorsque la déformation par flexion est très faible (r/t >6,5), on peut considérer que la couche neutre se situe approximativement au milieu de l'épaisseur du matériau, c'est-à-dire que le rayon de courbure de la couche neutre est de ρ=r+t/2.
Lorsque la déformation est très importante (r/t≤6,5), l'épaisseur du matériau devient plus fine et la distorsion de la section est très importante, comme le montre la figure 5-3.
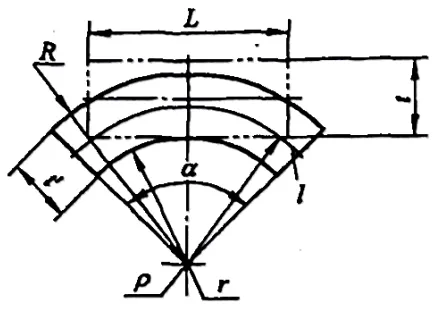
À ce moment-là, pour satisfaire à la condition d'équilibre selon laquelle la résultante de toutes les forces agissant dans la section est nulle, la couche neutre doit se déplacer vers la surface intérieure du matériau.
À ce stade, nous pouvons déterminer le rayon de courbure de la couche neutre à condition que le volume ne change pas au cours de la déformation plastique, c'est-à-dire le volume avant la flexion : V0=LBt, et le volume après flexion :
V=(R2-r2)α*B'/2.
Dans la formule, B est la largeur de l'ébauche (mm) ; B' est la largeur moyenne de l'ébauche après pliage (mm) ; α est l'angle du centre de pliage. Selon le principe que le volume est égal avant et après le pliage, nous avons V0=V, c'est-à-dire,
LBt=(R2-r2)α*B'/2, et L=(R2-r2)α*B'/2tB (5-1).
À partir de la contrainte et de la déformation nulles de la couche neutre, on obtient L=l=αρ, où L est la longueur avant déformation de la couche neutre (mm), et l est la longueur après déformation de la couche neutre (mm).
En substituant l'équation (5-1), on obtient ρ=(R2-r2)B'/2tB. Si l'on substitue R=r+t' à l'équation ci-dessus, on obtient une autre forme de l'équation ρ=(r/t+η/2)tβη (5-2)où β est le facteur de largeur, β=B'/B, et généralement lorsqu'une plaque large (B>3t) est pliée, on considère que β=1 ; η est le facteur d'amincissement, η=t'/t.
L'équation (5-2) est la formule permettant de calculer théoriquement la position de la couche neutre. Lors du calcul, nous devons connaître η, c'est-à-dire la règle d'amincissement. La valeur de η est indiquée dans le tableau 5-1.
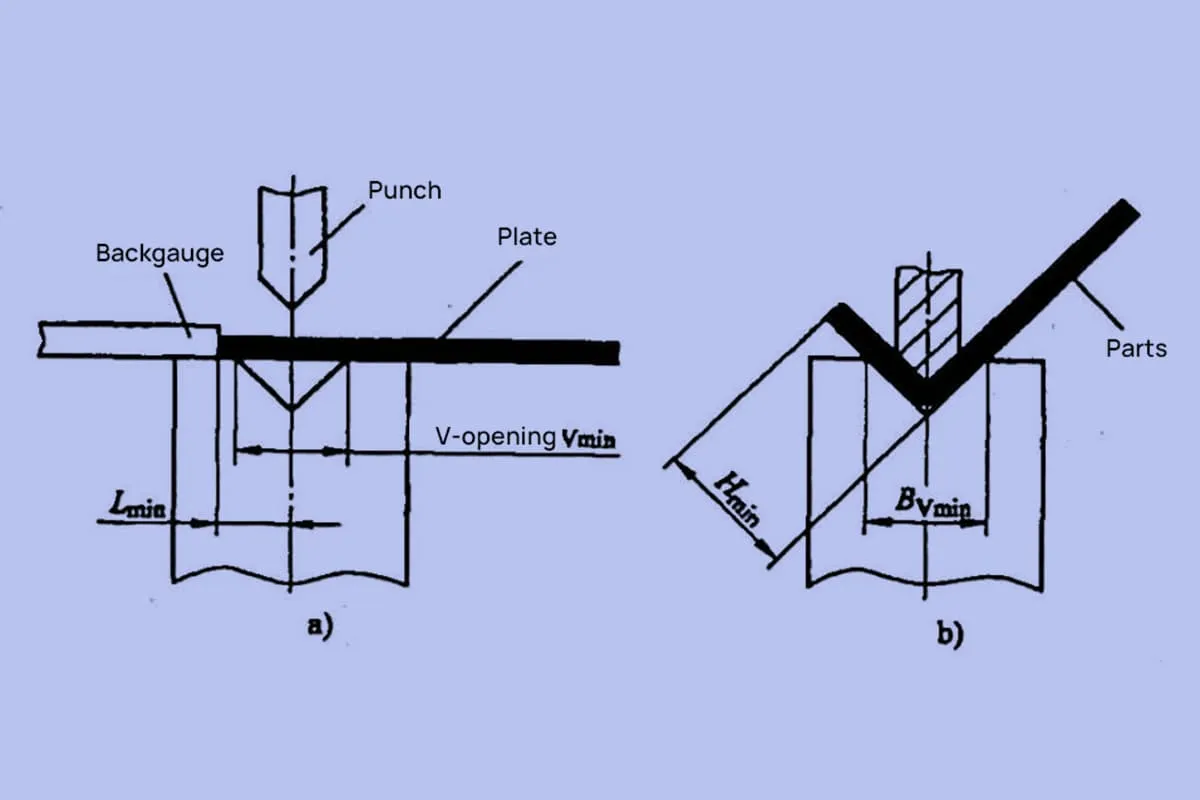
Il convient de souligner que la règle d'amincissement est assez complexe, que la répartition de la position de la couche neutre dans la zone de pliage n'est pas uniforme et que la règle d'amincissement est également liée à de nombreux facteurs tels que la méthode de pliage, la largeur de la fente de la matrice inférieure de pliage et l'épaisseur du matériau.
Cela entraîne des erreurs inévitables dans le calcul théorique de la position de la couche neutre, ce qui réduit la valeur d'application pratique de la méthode de détermination théorique.
Tableau 5-1 : Facteur d'amincissement η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
Dans la production réelle, une formule empirique, plus simple que le calcul théorique, est généralement utilisée pour déterminer la position de l'axe neutre, comme suit :
ρ = r + Kt (5-3)
Où ?
- ρ - Rayon de courbure de l'axe neutre (mm)
- r - Rayon de courbure intérieur de la matière première (mm)
- t - Epaisseur du matériau (mm)
- K - Coefficient de l'axe neutre (empirique) Facteur K), voir le tableau 5-2
Tableau 5-2 : Valeurs empiriques du coefficient de l'axe neutre K
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
Remarque :
- K1 s'applique aux coudes en V ou en U avec une plaque supérieure ou une plaque de presse.
- K2 convient aux coudes en forme de V sans plaque supérieure.
3. Calcul des dimensions de l'ébauche non pliée pour plusieurs coudes de tôle typiques
Sur la base de la définition de la couche neutre, la dimension dépliée de l'ébauche doit être égale à la longueur de la couche neutre. En règle générale, sur la base de l'épaisseur intérieure de la rayon de courbure r de l'ébauche, les coudes sont classés en coudes arrondis et non arrondis : les coudes sont considérés comme arrondis lorsque r>0,5t, et non arrondis lorsque r<0,5t.
En outre, en fonction de la largeur de la plaque B, les coudes sont classés en coudes à plaque larges et étroits : lorsque la largeur de la plaque B>3t, on parle de coude à plaque large, et lorsque la largeur de la plaque B<3t, on parle de coude à plaque étroit.
Dans la pratique, les coudes avec un rayon d'angle rond (r>0,5t) et des plaques larges (B>3t) sont les plus utilisés, et compte tenu de l'universalité des coudes, nous discutons principalement du calcul des dimensions dépliées des flans pour les coudes avec un rayon d'angle rond et des plaques larges pendant le cintrage.
3.1 Calcul des dimensions de l'ébauche non pliée pour les coudes à angle droit (r>0,5t)
Lorsque r>0,5t, B>3t, du fait que l'amincissement de la partie pliée n'est pas important et que la distorsion de la section transversale est faible, la longueur du flan peut être déterminée sur la base du principe selon lequel la longueur de la couche neutre est égale à la dimension dépliée du flan.
Les méthodes courantes de calcul des dimensions des pièces brutes dépliées des coudes à angle droit (r>0,5t) se divisent en deux catégories : le calcul du coefficient de flexion et le calcul de la valeur de déduction de la flexion.
1. Coudes à coins arrondis (r>0,5t) Calcul du coefficient de flexion pour les dimensions de l'ébauche non pliée :
1) Le coefficient de flexion est la longueur de la partie de l'arc mesurée le long de la couche neutre de la zone de déformation par flexion (partie R de la flexion), comme le montre la figure 5-4.
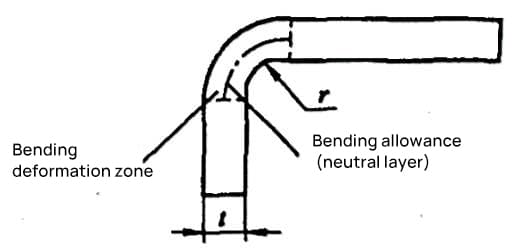
Le coefficient de flexion est calculé par la formule (5-4) : x=παρ/180° (5-4)
Où ρ est le rayon de courbure de la couche neutre (mm).
2) La figure 5-5 montre un exemple de notation des dimensions pour le calcul du coefficient de flexion des dimensions dépliées du flan, et sa formule de calcul du coefficient de flexion des dimensions dépliées du flan est la suivante.

a) φ > 90° b) φ≤90
L=a+b+x (5-5)
En substituant l'équation (5-3) à l'équation (5-4), on obtient la formule du coefficient de flexion :
x=πα(r+Kt)/180° (5-6)
En substituant l'équation (5-6) à l'équation (5-5), on obtient la formule de calcul de la taille dépliée de l'ébauche pliée :
L=a+b+πα(r+Kt)/180° (5-7)
Où ?
- L - La taille dépliée de la feuille blanche (mm) ;
- K - Coefficient du facteur K, voir tableau 5-2 pour sa valeur ;
- α - L'angle central de flexion, sa relation avec l'angle de la partie pliée est α=180°-φ ;
- r - Le rayon de courbure de la couche intérieure de l'ébauche (mm) ;
- t - L'épaisseur du matériau (mm) ;
- a, b - Les longueurs des parties droites du composant (mm), respectivement.
2. Calcul de la déduction de flexion pour la taille dépliée d'une pièce pliée à angle arrondi (r>0,5t)
1) La déduction de flexion (également appelée valeur de correction pour la partie R) est la différence entre deux fois le R de la zone de déformation de la flexion (la partie R de la flexion) et le coefficient de flexion, comme le montre la figure 5-6.

La déduction pour flexion (valeur de correction pour la partie R) est calculée selon l'équation (5-8) :
y = 2R-παr/180° (5-8)
2) La figure 5-7 montre un exemple d'annotation de dimension pour le calcul de la déduction pour flexion pour la taille dépliée de l'ébauche. La déduction pour flexion y est calculée à l'aide de la formule suivante :
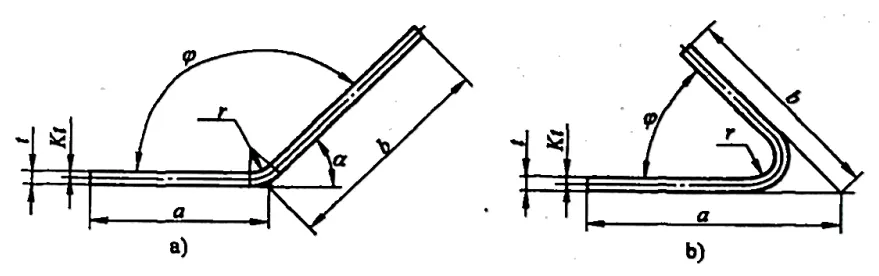
a)90°<φ≤165° b)φ≤90°
①Lorsque φ ≤ 90° :
R=(r+t)/tan(φ/2)
En substituant la formule ci-dessus et la formule (5-3) dans la formule (5-8), on obtient la déduction de flexion (c'est-à-dire la valeur de correction de la partie R) pour une courbure φ≤90° (voir figure 5-7b) :
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
②Lorsque 90°<φ≤165° :
R=(r+t)tan[(180°-φ)/2]
En substituant la formule ci-dessus et la formule (5-3) à la formule (5-8), nous obtenons la déduction de flexion (c'est-à-dire la valeur de correction de la partie R) pour une flexion de 90°<φ≤165° (voir figure 5-7a) :
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
③Lorsque 165°<φ≤180° :
y≈0
3) La formule de calcul de la valeur de la déduction pour flexion de la taille de l'ébauche de la pièce illustrée à la figure 5-7 est la suivante :
L=a+b-y (5-11)
①Lorsque φ≤90°, en substituant la formule (5-9) à la formule (5-11), on obtient la formule de calcul de la valeur de déduction de la flexion de la taille de l'ébauche comme suit :
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
②Lorsque 90°<φ≤165°, en substituant la formule (5-10) à la formule (5-11), on obtient la formule de calcul de la valeur de déduction de la flexion de la taille de l'ébauche comme suit :
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
③Lorsque 165°<φ≤180° :
L≈a+b (5-14)
Où ?
- y - Déduction pour flexion (mm)
- L - Taille de l'ébauche de la pièce (mm)
- r - Rayon de courbure intérieur de l'ébauche (mm)
- t - Epaisseur du matériau (mm)
- α - Angle du centre de flexion, sa relation avec l'angle de flexion est α=180°-φ
- a, b-Longueurs des arêtes de la pièce (mm) jusqu'au sommet de flexion.
3. Calcul de la taille de l'ébauche pour les coudes à angles multiples
Pour les coudes à angles multiples, la taille de l'ébauche est la somme de la partie R et des longueurs des bords droits.
1) Calcul de la taille de l'ébauche de pliage à angles multiples par le coefficient de flexion :
L=l1+l2+...+ln+1+nx (5-15)
Où l1, l2...ln+1 sont les longueurs des parties droites de chaque bord de la pièce (mm) ;
n est le nombre de coudes R.
2) Calcul de la taille de l'ébauche de pliage à angles multiples par la déduction du pliage :
L=l1+l2+...+ln+1-ny (5-16)
Où l1, l2...ln+1 sont les longueurs des bords de la pièce (mm) jusqu'au sommet de flexion ;
n est le nombre de coudes R.
Exemple 5-1 : Calculer la taille de l'ébauche pour le coude illustré à la figure 5-8.
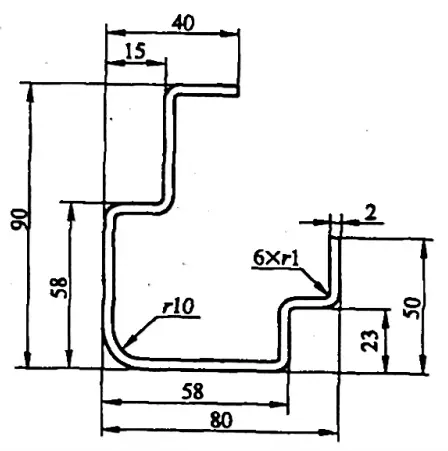
Solution 1 : Calculer la taille de l'ébauche à l'aide du coefficient de flexion.
Voir l'annexe A : Lorsque l'angle de la pièce à plier φ=90°, l'épaisseur t=2mm et le rayon r=10mm, le coefficient de flexion est de 2,68mm ;
Lorsque l'angle de la pièce à plier est de 90°, l'épaisseur t=2mm et le rayon r=10mm, le coefficient de flexion est de x2=16,9mm.
A partir des équations (5-5) et (5-15), la dimension plate de l'ébauche pour la pièce pliée est calculée comme suit :
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2,68 + 16,9]mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240,98 mm.
Solution 2 : Calculer la taille à plat de l'ébauche à l'aide de la valeur de la déduction pour le pliage.
Voir l'annexe C : pour un coude avec un angle φ=90°, une épaisseur t=2mm et un rayon r=1mm, la valeur de correction pour la section R est y1=3,32mm ; pour un coude avec un angle φ=90°, une épaisseur t=2mm et un rayon r=10mm, la valeur de correction pour la section R est y2=7,1mm.
La taille brute de la pièce pliée peut être obtenue à partir des équations (5-11) et (5-16) :
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3,32 - 7,1] mm
= (25+34+17+116+25+24+27-19,92-7,1) mm
= 240,98 mm
Exemple 5-2 : calculer la taille brute de la pièce pliée illustrée à la figure 5-9.
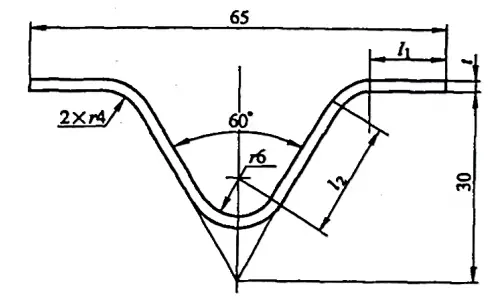
Solution : Calculer la taille brute à l'aide du coefficient de flexion.
La formule pour calculer les dimensions de l'ébauche de la pièce pliée à partir des équations (5-5) et (5-15) est la suivante :
L=2l1+2l2+2x1+x2
où l1 = [32,5 - (30tan30°+4tan30°)] mm = 12,87 mm
et l2 = [(30/cos30°) - (8/tan30°+4tan30°)] mm = 18,47 mm
Référence à l'annexe A : lorsque l'angle de courbure φ=120°, t=2mm, r=4mm, la valeur du facteur de courbure est x1=4,98mm ; lorsque l'angle de courbure φ=60°, t=2mm, r=6mm, la valeur du facteur de courbure est x2=14,16 mm.
En substituant ces valeurs à la formule, on obtient la longueur dépliée du blanc : L= (2×12,87 + 2×18,47 + 2×4,98 + 14,16) mm = 86,8 mm.
Il convient de noter que pour les pliages plus simples avec des exigences de précision moindres, les dimensions de l'ébauche dépliée peuvent être directement calculées. Toutefois, pour les cintrages plus complexes ou ceux dont les exigences de précision sont plus élevées, la forme et les dimensions de l'ébauche dépliée doivent être testées et révisées à plusieurs reprises afin de confirmer la forme et les dimensions de l'ébauche.
3.2 Calcul des dimensions de développement des flans pour les composants à forte courbure (r<0,5t)
Lorsque le rayon de courbure r d'un composant est inférieur à 0,5 t, on parle de courbure forte. Le calcul de la dimension de développement de l'ébauche pour de tels composants est basé sur le principe de la cohérence des volumes avant et après le cintrage.
Dans le cas des pliages serrés, en raison de l'amincissement important du matériau au niveau du pliage, le processus de déformation est extrêmement complexe, ce qui rend difficile le calcul précis des dimensions de développement de l'ébauche. Par conséquent, les dimensions de développement de l'ébauche calculées doivent être corrigées sur la base de données empiriques ou par le biais d'essais de pliage.
La formule de calcul des dimensions de développement des pièces brutes pour les composants à forte courbure (r<0,5t, φ=90°) est présentée dans le tableau 5-3.
Tableau 5-3 Formule de calcul des dimensions de développement des pièces brutes pour les composants à forte courbure (r<0,5t, φ=90°) (unité : mm)
| Numéro de série | Caractéristiques de pliage | Schéma | Formule |
| 1 | Plier un coin. |  | L=a+b+0,4t |
| 2 | L'aplatir. |  | L=a+b-0,43t |
| 3 | Plier deux coins à la fois. | 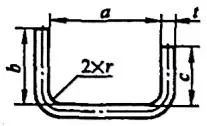 | L=a+b+c+0,6t |
| 4 | Plier les trois coins simultanément. | 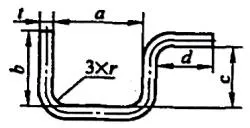 | L=a+b+c+d+0,75t |
| 5 | Plier deux coins dans le premier cas, et plier un autre coin dans le second. | L=a+b+c+d+t | |
| 6 | Plier les quatre coins en même temps. | 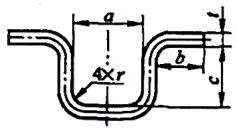 | L=a+2b+2c+1,2t |
| 7 | Plier pour former quatre coins en deux fois. | L=a+2b+2c+1,2t |
3.3 Calcul des dimensions non pliées pour les pièces à plier de type charnière
Pour le type de charnière pièces de pliage avec r= (0,6~3,5)t (voir figure 5-10), le processus de bordage suit généralement le schéma de la figure 5-11. Pendant le bordage, l'épaisseur de la tôle augmente et la couche neutre se déplace vers l'extérieur. Les dimensions dépliées de l'ébauche peuvent être calculées approximativement à l'aide de la formule suivante :
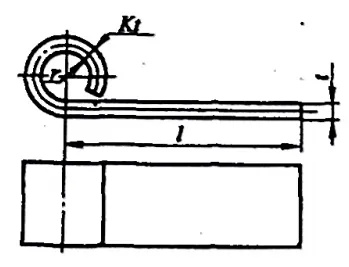
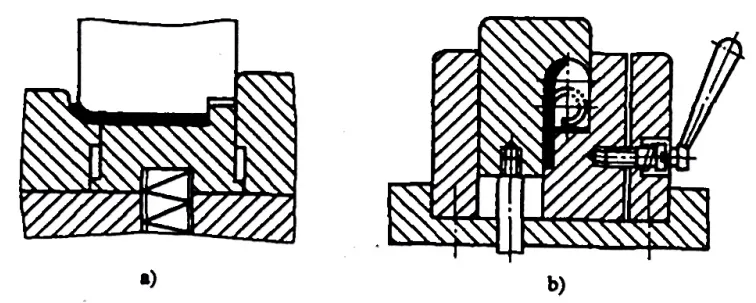
- a) Première opération
- b) Deuxième opération
L=l+1.57π(r+Kt)+r
Où ?
- L - Dimensions non pliées de la découpe (mm) ;
- l - Longueur du segment droit (mm) ;
- r - Rayon de courbure interne de l'ébauche (mm) ;
- K - Coefficient de déplacement de la couche neutre. Lorsque r/t=0,5~1,8, K est généralement compris entre 0,5~0,70 (plus la valeur de r/t est petite, plus la valeur de K est grande ; inversement, plus la valeur de K est petite). Il peut également être sélectionné selon le tableau 5-4.
Tableau 5-4 Coefficient de déplacement de la couche neutre pour les pièces pliées de type charnière
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |