La force de flexion est une base importante pour la conception des processus d'emboutissage, le choix des presses et la conception des moules.
Étant donné que l'ampleur de la force de flexion dépend non seulement de la taille de l'ébauche, des propriétés mécaniques du matériau, de la distance entre les supports de la matrice, du rayon de flexion et de l'espace entre les moules, mais aussi en grande partie de la méthode de flexion, il est difficile d'effectuer des calculs précis à l'aide de méthodes d'analyse théoriques. Par conséquent, en production, les formules empiriques énumérées dans le tableau 1 sont généralement utilisées pour un calcul approximatif de la force de flexion.
I. Base de calcul théorique et méthodes pour la force de flexion
La méthode de calcul théorique de la force de flexion est dérivée des conditions d'équilibre statique selon lesquelles la somme des diverses forces externes agissant sur l'ébauche de flexion est nulle, et le couple externe agissant sur l'ébauche de flexion est égal à son couple de résistance interne, par le biais d'un calcul conventionnel.
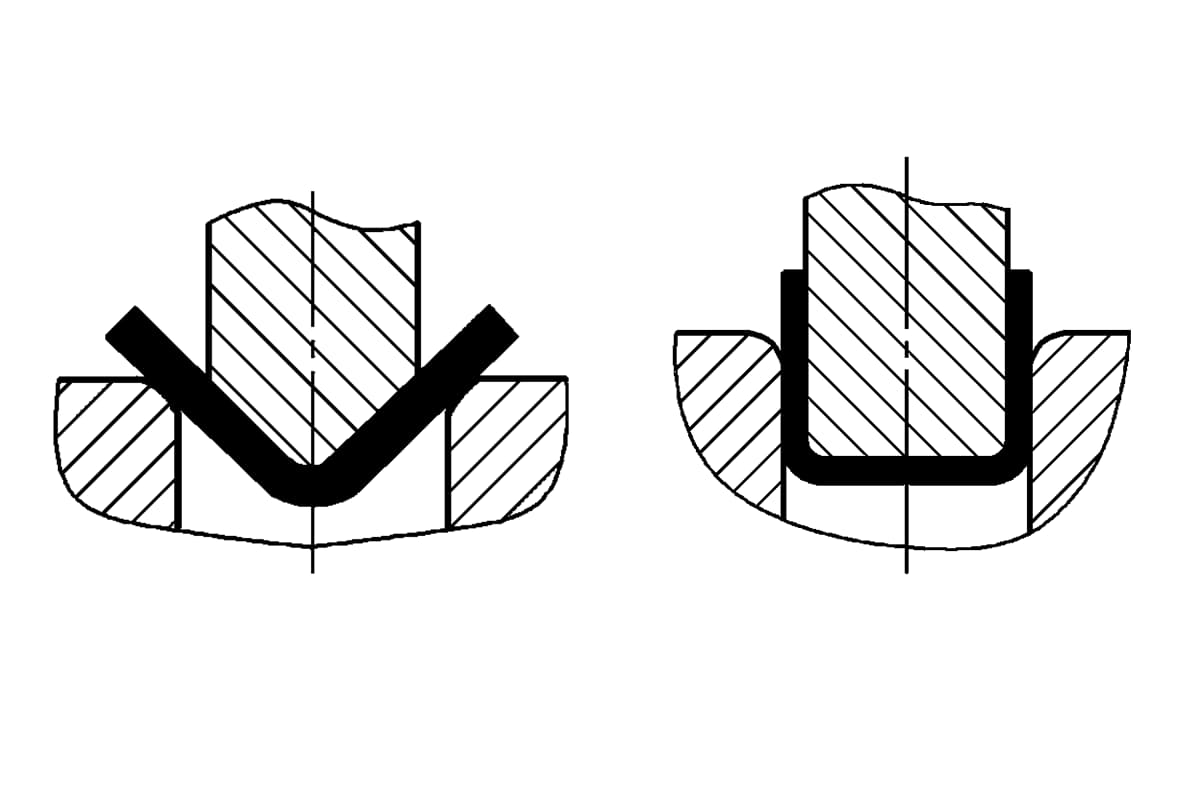
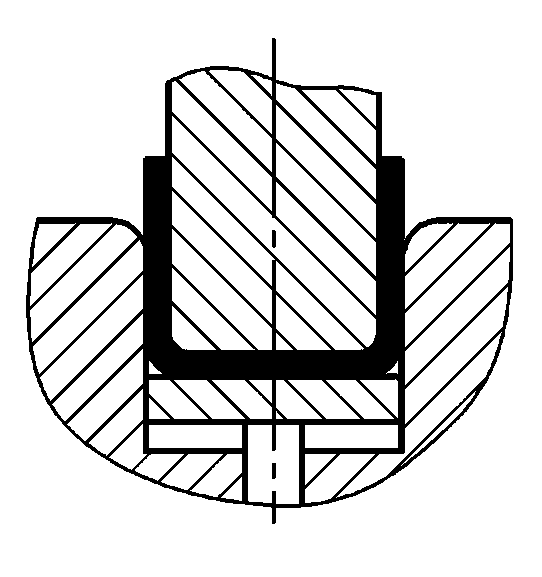
La méthode de pliage et la structure de la matrice modifient l'état de contrainte de l'ébauche de pliage. Les différentes méthodes de cintrage donnent lieu à des pressions de cintrage très différentes. Si l'on prend les formes en V et en U couramment utilisées, on obtient des pressions de cintrage très différentes. pièces de pliage à titre d'exemple, comme le montre la figure 1, ils peuvent être formés par cintrage à l'aide de matrices de cintrage ordinaires en acier plein, en utilisant respectivement le cintrage libre, le cintrage de refoulement par contact et le cintrage de correction d'impact.
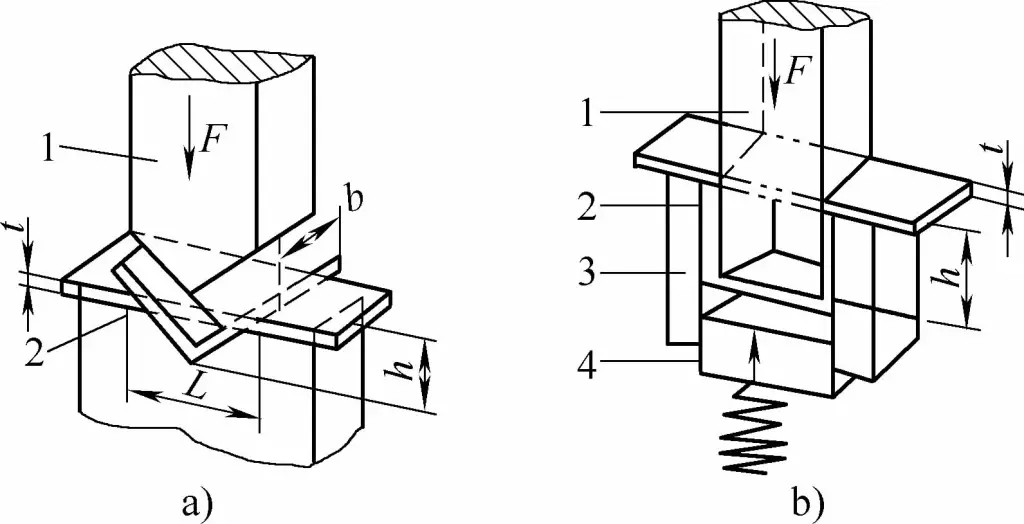
- a) Pièces de flexion en forme de V
- b) Pièces de flexion en U
- 1 - Poinçon de pliage
- 2 - Pièce à plier
- 3 - Matrice de pliage en U
- 4 - Outil supérieur
- L - Largeur de l'ouverture de la filière en U
- t - Epaisseur de la pièce de flexion
- h - Profondeur de la cavité de la matrice de pliage en forme de V
Les pièces pliées en forme de V utilisent une charge concentrée au milieu de deux supports d'une ébauche plate pour le pliage pur et le pliage libre, principalement utilisés sur les chantiers de construction. En ligne, les pièces de tôlerie de petite et moyenne taille sont principalement formées par le cintrage à refoulement par contact, et les pièces de tôlerie de moyenne épaisseur à haute résistance sont souvent pliées sur des presses à friction en utilisant le cintrage à correction d'impact. Le pliage libre nécessite moins de pression, sans pression supplémentaire, seulement une simple force de pliage.
II. Calcul de la force de flexion par différentes méthodes de flexion
Les formules de calcul de la force de flexion selon différentes méthodes de flexion sont présentées dans le tableau 1.
Tableau 1 Formules de calcul de la force de flexion selon différentes méthodes de flexion
| Nom | Schéma | Caractéristiques de la déformation par flexion | Formule de calcul de la force de flexion | ||
| Théorique | Approximatif | Recommandé | |||
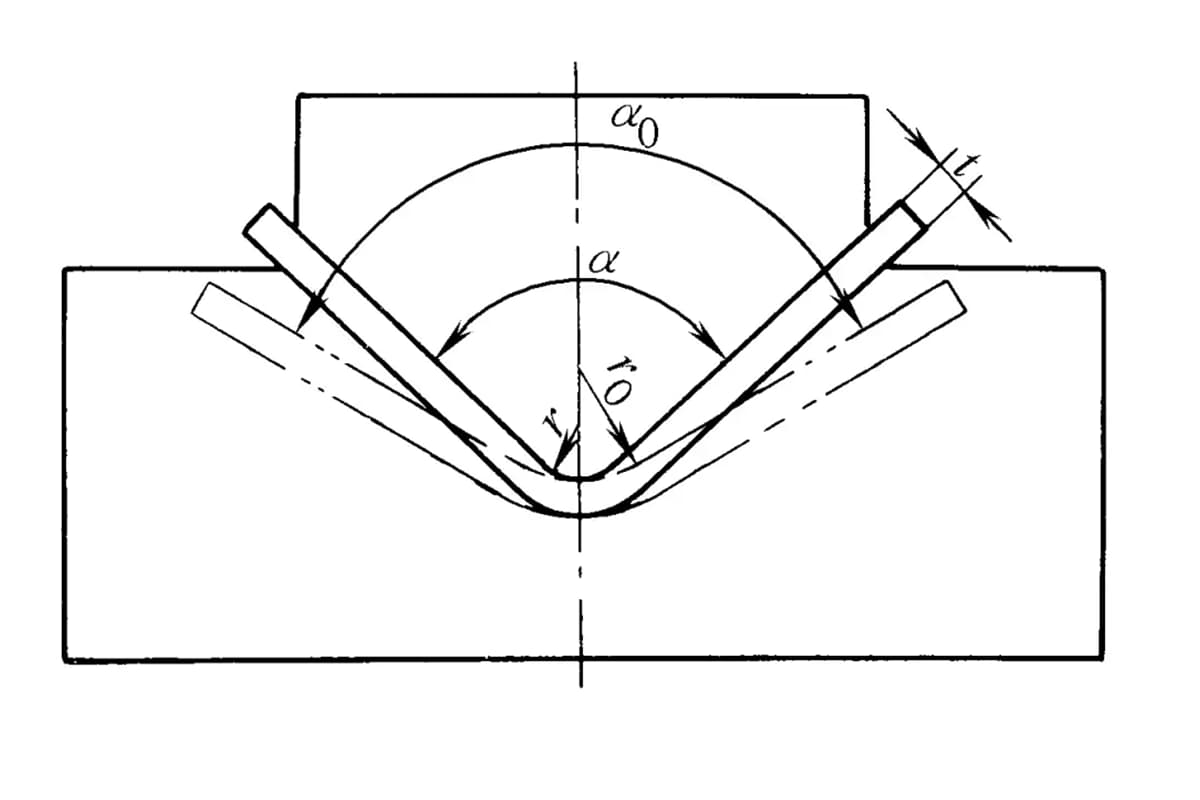
| Flexion libre à angle unique (partie courbée en forme de V) | 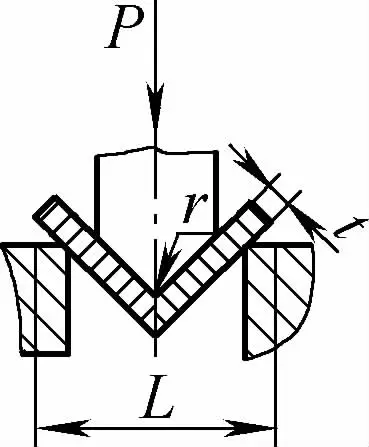 | L'ébauche est pliée au milieu en appliquant une pression sur deux supports à l'entrée de la matrice, la partie inférieure n'entrant pas en contact avec le moule. | Lorsque 2r≤L, F=0,7bt3 Rm /(r+t) Lorsque 2r>L, F=2bt2 Rm /3L | F = KbtRm | F=Cbt2Rm/L |
| Cintrage par contact à angle unique (pièces de flexion en forme de V) | 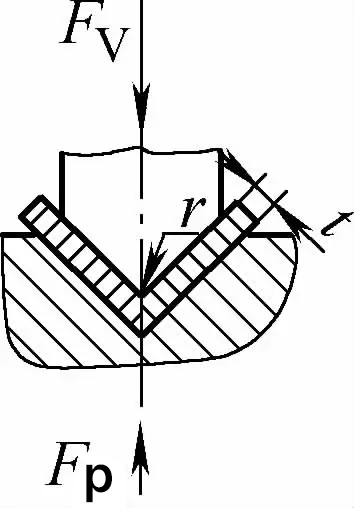 | Avant que le processus de cintrage ne soit terminé, l'ébauche de cintrage est en contact étroit avec l'ensemble de la cavité du moule. Une plaque de pression est généralement utilisée pour réaliser le cintrage. écart de filière supérieur ou égal à t | Lorsque 2r≤L, Fv =0,7bt2 Rm /(r+t)+Fp Lorsque 2r>L, Fv =2bt2 Rm /3L+Fp | Fv=KbtRm +Fp | Fv=2Cbt2Rm/L |
| Contact à angle unique avec cintrage de correction d'impact (pièces de cintrage en forme de V) | 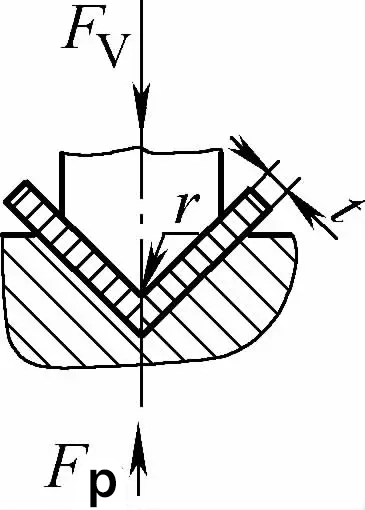 | Basé sur le cintrage par contact, il a également la fonction de correction d'impact. L'écart entre les matrices de pliage est généralement inférieur ou égal à t | Fv=0,7bt2Rm/L+Fp+qAb | Fv=1,3qAb | Fv=1,39qAb |
| Flexion libre à double angle (pièces pliées en forme de U) | 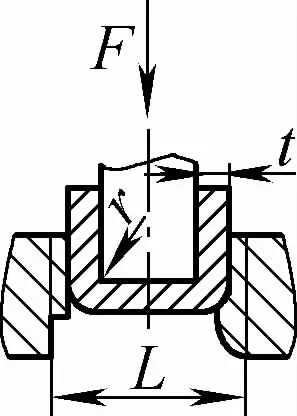 | L'ébauche est pliée au milieu en appliquant une pression sur deux supports à l'entrée de la matrice, la partie inférieure de l'ébauche n'entrant pas en contact avec le moule. | Lorsque 2r≤L, F=0,7bt 2 Rm /(r+t) Lorsque 2r>L, F=2bt 2 Rm /3L | F =KbtRm | F=0.4CKbtRm |
| Cintrage par contact à double angle (pièces de cintrage en U) | 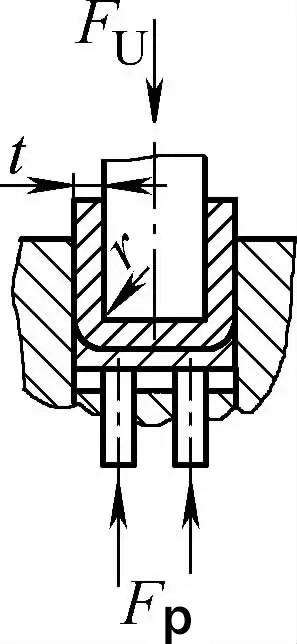 | Lors du pliage, une plaque de pression est utilisée ou un écart égal ou légèrement supérieur à t est utilisé, mais il n'y a pas de fonction de correction d'impact. | Lorsque 2r≤L, Fu =0,7bt2Rm /(r+t)+Fp Lorsque 2r>L, Fu =2bt2Rmn/3L+Fp | Fu =KbtRm +Fp | Fu=0,5CbtRm |
| Contact à double angle avec courbure de correction d'impact (pièces de courbure en forme de U) | 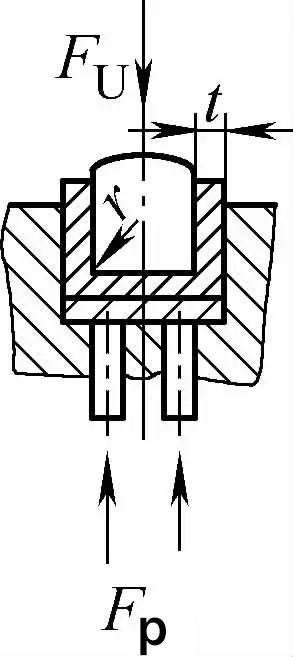 | Pendant le pliage, un espace de pliage inférieur ou égal à t est utilisé avec une plaque de pression (plaque supérieure) et a également la fonction de correction d'impact. | Fu=0,7bt2Rmn/L+Fp+qAb | Fu=1,3qAb | Fu=1,3qAb |
Note : La signification des symboles dans le tableau est la suivante :
- b - largeur de la partie à plier (mm) ;
- R - résistance à la traction du matériau de la pièce à plier (MPa) ;
- L - longueur de l'ébauche de pliage aux points d'appui de part et d'autre de l'ouverture de la matrice de pliage (mm) ;
- C - coefficient, pour une flexion à angle unique L>10t, C=1 ; pour une flexion à angle double r=t, C=1 ; n-nombre d'angles de flexion (pièces) ;
- A - surface d'appui de la pièce à plier (mm²) ;
- F - pression de correction plate (kN), généralement 30%~100% de la force de flexion ;
- K - coefficient du type de matériau, dont la valeur est indiquée dans le tableau 2 ;
- q - pression de correction de l'unité (impact) (MPa), la valeur peut être trouvée dans le tableau 3.
Tableau 2 Type de matériau coefficient K valeur
| Matériau | Rapport L/t | |||||
| 3 | 10 | 15 | 20 | 25 | 30 | |
| 10 acier, 15 acier, laiton, aluminium (doux) | 0.23 | 0.18 | 0.12 | 0.09 | 0.073 | 0.060 |
| 20 acier, 25 acier, aluminium trempé | 0.21 | 0.17 | 0.11 | 0.08 | 0.070 | 0.057 |
| 20 acier, 25 acier, 40 acier, aluminium super dur | 0.20 | 0.16 | 0.10 | 0.08 | 0.065 | 0.053 |
Tableau 3 Valeur approximative de la pression de correction unitaire (impact) q pendant la flexion (unité : MPa)
| Matériau | Épaisseur du matériau de flexion t/mm | |
| ≤3 | >3~10 | |
| Aluminium | 30~40 | 50~60 |
| Laiton | 60~80 | 80~100 |
| 10 acier, 15 acier, 20 acier | 80~100 | 100~120 |
| 25 acier, 30 acier, 35 acier | 100~120 | 120~150 |
Formules de calcul de la force de flexion
Tableau 4 Formules empiriques pour le calcul de la force de flexion
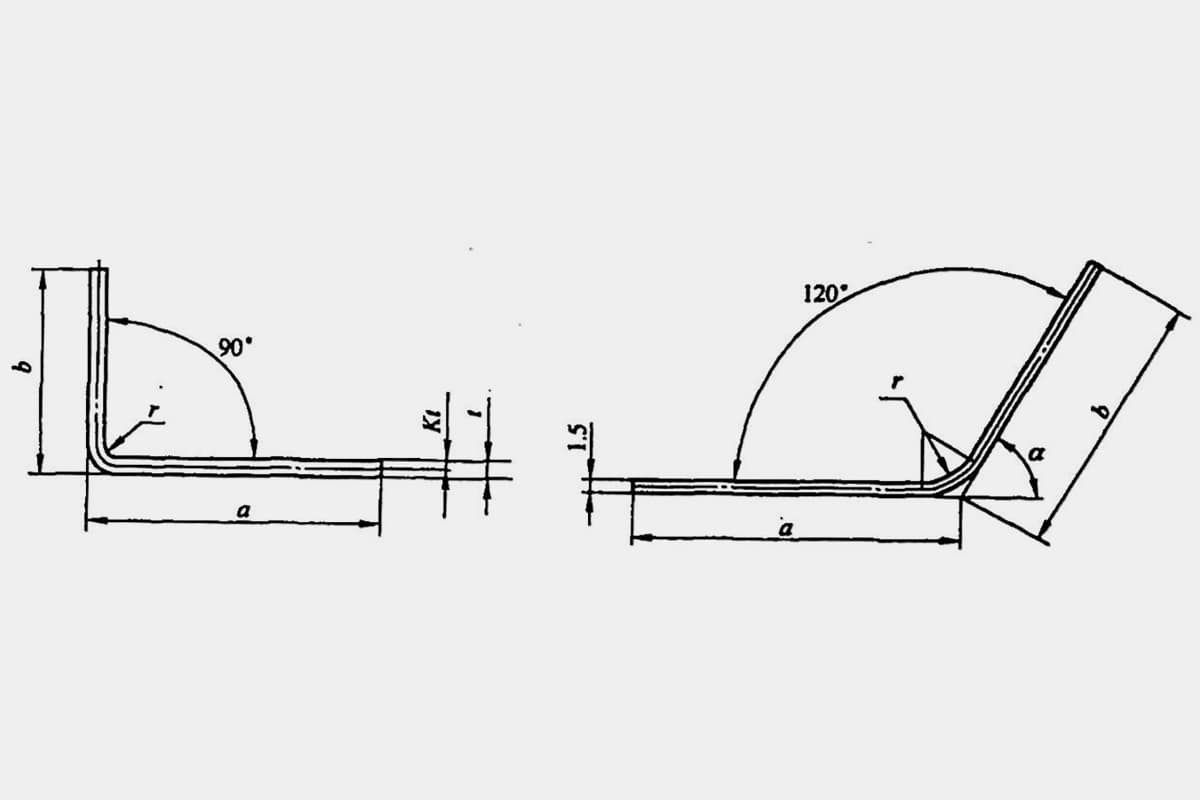
| Méthode de pliage | Schéma | Formules empiriques | Notes |
| Cintrage libre | 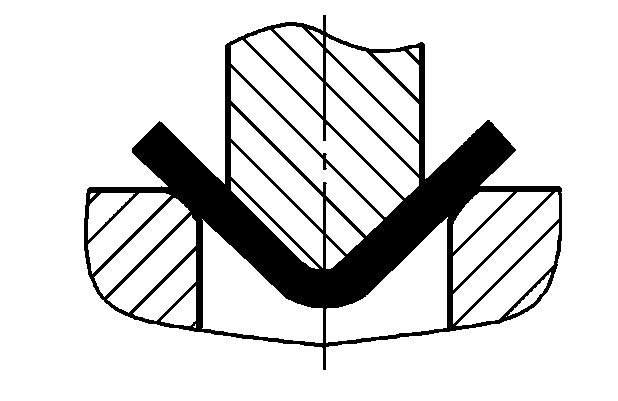 | P=(0,8Bt2σb)/(r+t) | où P-Force de flexion totale (N) B-Largeur de la partie pliée (mm) t-Épaisseur du matériau (mm) σb-Résistance à la traction (MPa) r-Intérieur rayon de courbure (mm) Zone de projection de la partie de correction A (mm)2 ) Pression de correction unitaire (MPa), voir tableau 5 pour sa valeur |
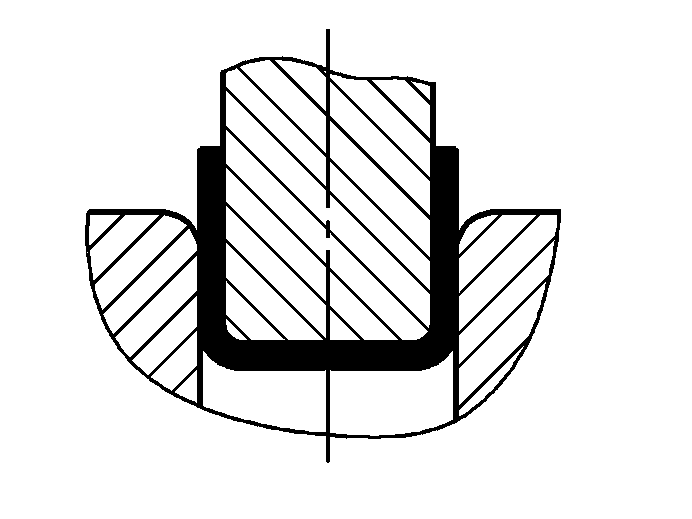 | P=(0,9Bt2σb)/(r+t) | ||
| Pliage avec correction | 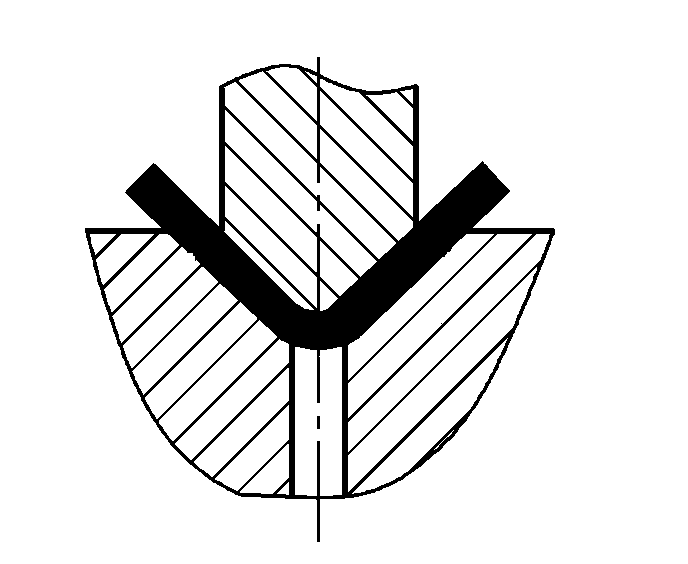 | P=(1,4Bt2σb)/(r+t) | |
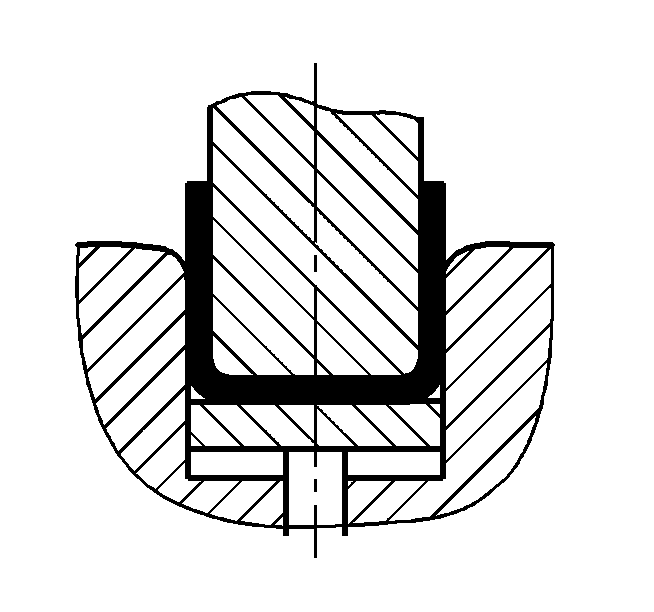 | P=(1,6Bt2σb)/(r+t) | ||
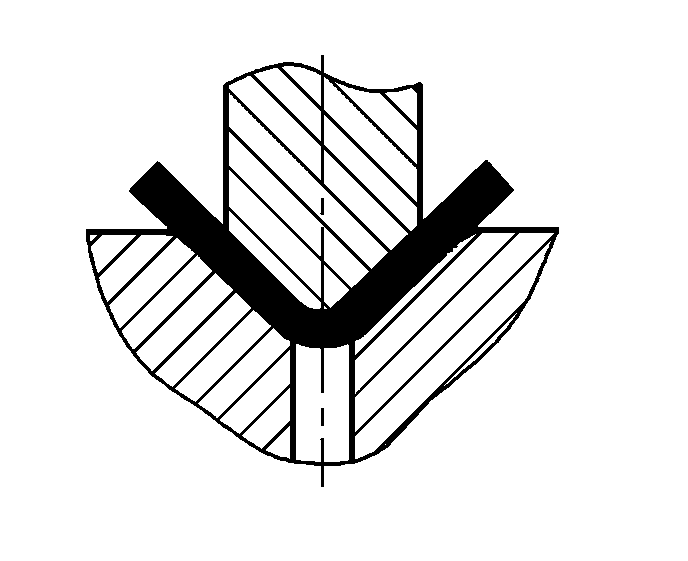 | P=(1,4Bt2σb)/(r+t)+Aq | ||
 | P=(1,6Bt2σb)/(r+t)+Aq |
Tableau 5 Correction unitaire de la pression q (unité : MPa)
| Matériau | Epaisseur du matériau / mm | |||
| <1 | 1~3 | 3~6 | 6~10 | |
| Aluminium | 15~20 | 20~30 | 30~40 | 40~50 |
| Laiton | 20~30 | 30~40 | 40~60 | 60~80 |
| 10~20 acier | 30~40 | 40~60 | 60~80 | 80~100 |
| 25~30 acier | 40~50 | 50~70 | 70~100 | 100~120 |
III. Calcul du travail de flexion
Le travail de flexion des pièces cintrées en V peut être calculé à l'aide de la formule suivante.
Wv=mFvh
Où
- Wv - Le travail de cintrage des pièces cintrées en V (J), généralement calculé par le cintrage de refoulement par contact ;
- m - Coefficient de correction, m=0,32 pour les pièces de flexion en V, m=0,63 pour les pièces de flexion en U ;
- Fv - Force de flexion des pièces de flexion en forme de V (kN), F v ou F u La force de flexion peut être calculée à l'aide de la formule de calcul appropriée du tableau 1.
- h - Profondeur de la cavité de la matrice de cintrage (c'est-à-dire la course de cintrage) (mm), h peut également être calculé à l'aide de la formule suivante.
h=0,5L~0,4(t+r)
Où
- L - Distance entre les deux points d'appui des pièces de cintrage en V sur l'ouverture de la matrice de cintrage (mm) ;
- t - Epaisseur des pièces de flexion (mm) ;
- r - Rayon de courbure (mm).
IV. Méthode graphique simplifiée pour la force de flexion et le travail de flexion
La figure 2 présente le tableau à colonnes de calcul graphique pour la force de flexion et le travail de flexion des pièces cintrées en V et en U. Ce tableau est pratique à utiliser, le calcul graphique est rapide et les résultats sont proches de la réalité. Ce tableau est pratique à utiliser, le calcul graphique est rapide et les résultats sont proches de la réalité, ce qui permet une utilisation sur site.
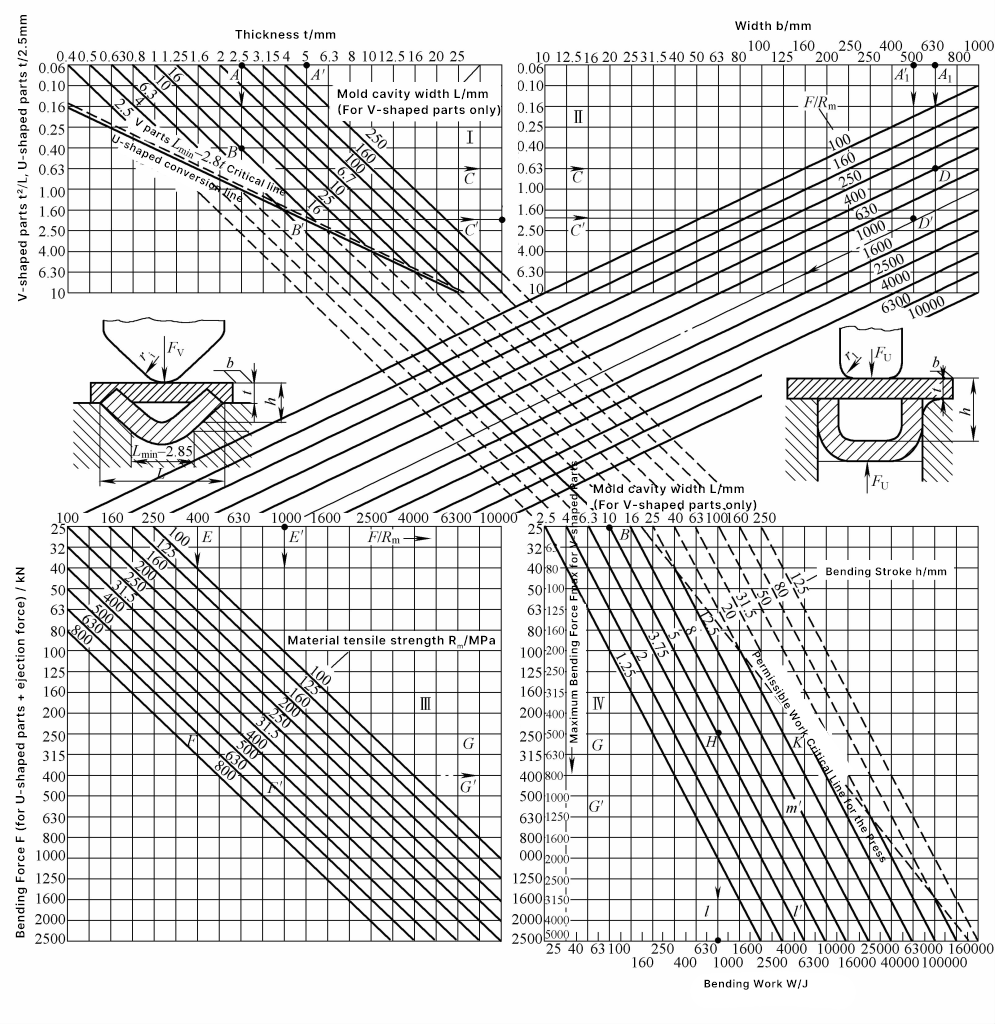
Note : Les symboles dans le tableau signifient ce qui suit :
- F - Force de flexion des pièces en V et en U (kN) ;
- W - Travaux de cintrage de pièces en V et en U (J) ;
- H - Course de travail de cintrage des pièces en V et en U (mm) ;
- L, L min - Largeur d'ouverture de la matrice de pliage pour les pièces pliées en V (mm), largeur d'ouverture minimale (mm) ;
- r - Rayon de courbure intérieur des pièces à plier (mm) ;
- t - Epaisseur des pièces de flexion (mm).
Exemple de calcul graphique. Étant donné une pièce à plier en forme de V avec t=2,5mm, la largeur d'ouverture de la matrice de pliage L=10mm. Dans la zone I de la figure 2, t2/L=0,63 (voir ligne ABC). Etant donné la largeur de la pièce à plier b=630mm, la résistance à la traction du matériau R m =630MPa, dans les zones II et III, trouver les valeurs A1 DEF, et dans la zone III, le long de la ligne d'extension droite, trouver la ligne FG, ce qui donne une force de flexion Fv =250kN.
Dans la zone IV, compte tenu de la pression de nivellement et de redressement, la pression totale est F∑ =2F=500kN. La course de travail de flexion h=0,5L=5mm, le coefficient de correction m=0,32, donc le travail de flexion Wv =mF∑ h=800J, comme le montrent les lignes BH et CHI de la figure 2.