Durante o processo de criação do desenho de desenvolvimento do componente de chapa metálica, é também necessário considerar o impacto da espessura do material de processamento, ou seja, efetuar os ajustamentos adequados da espessura da chapa.
De um modo geral, para materiais em folha com uma espessura inferior a 3 mm, não é necessário qualquer ajuste da espessura da placa. Pode ser calculado de acordo com o diâmetro central do material em folha ou de acordo com as linhas de corte da superfície interior e exterior. As dimensões após a formação estão dentro do intervalo de desvio permitido. Quando a espessura da chapa é superior a 3 mm, deve ser calculada de acordo com o diâmetro central do material da chapa. Por conveniência de descrição, os cálculos para os seguintes materiais desenvolvidos referem-se ao diâmetro central do material da folha.
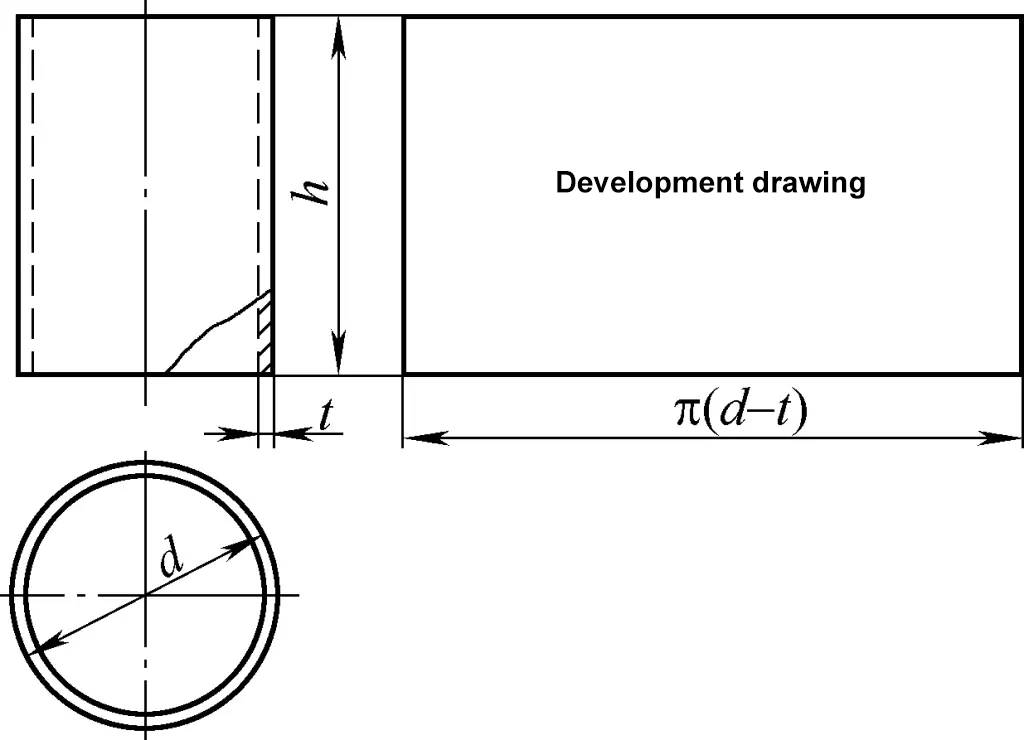
1. Cálculo do desenvolvimento de cascas cilíndricas
A casca cilíndrica pertence à superfície cilíndrica, e o seu desenho de desenvolvimento é um retângulo. Um dos lados do retângulo é igual à circunferência do cilindro π(d-t), e o outro lado é a altura h do cilindro, como se mostra na Figura 1. Na figura, d é o diâmetro exterior do cilindro e t é a espessura da placa.
2. Cálculo do desenvolvimento de cones circulares rectos
O desenho de desenvolvimento do cone circular direito é um arco de sector. A fórmula de cálculo para o desenho de desenvolvimento do cone circular direito mostrado na Figura 2 é:
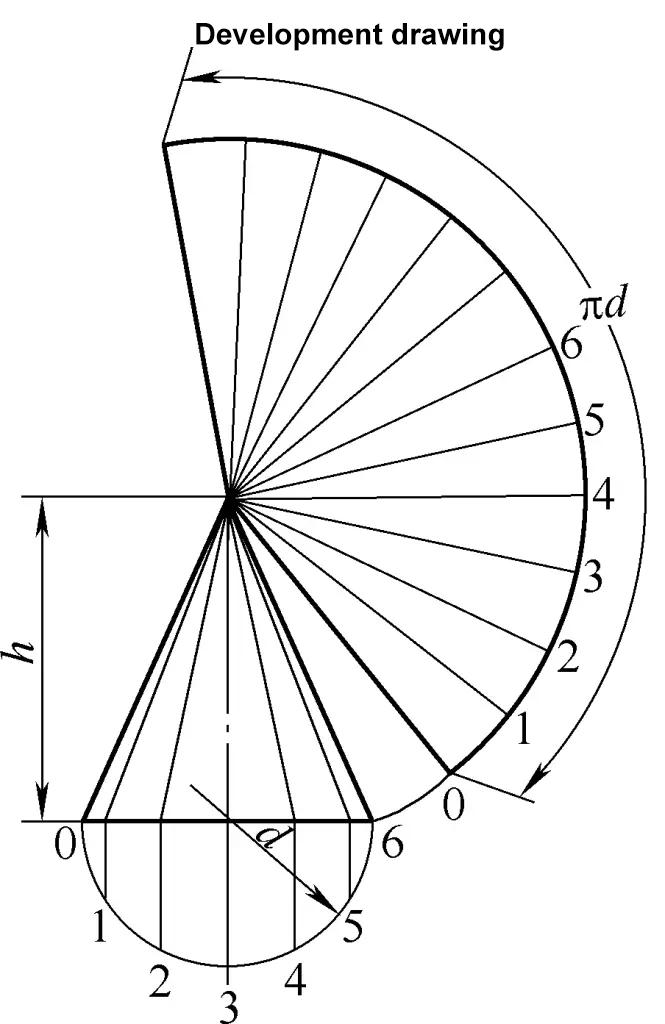
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
Na fórmula
- R - Raio do arco de sector (mm);
- α - Ângulo do sector (°);
- L - Comprimento da corda do arco de sector (mm).
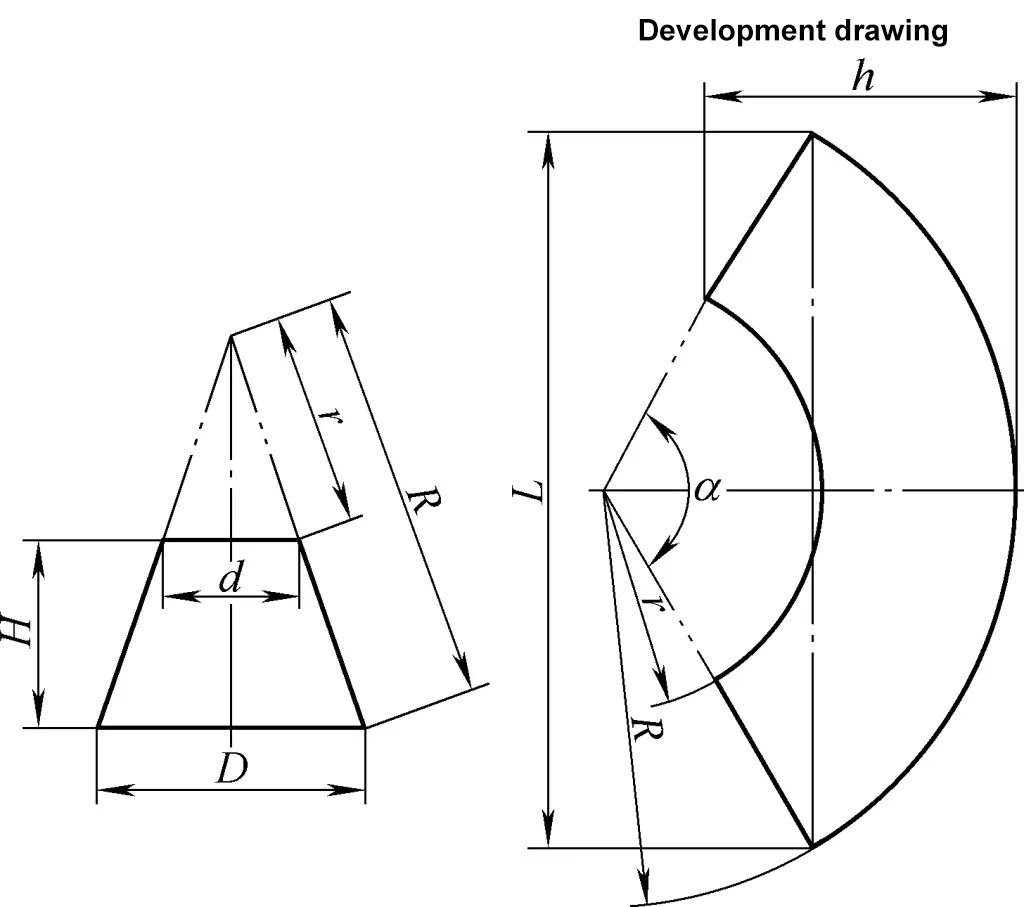
3. Cálculo do desenvolvimento de cones circulares rectos truncados
O desenho de desenvolvimento do cone circular truncado à direita é um arco de sector concêntrico. A fórmula de cálculo para o desenho de desenvolvimento do cone circular truncado à direita mostrado na Figura 3 é
R=√{(D/2)2+[DH/(D-d)]2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
Quando α>180°, h=R+rsin[(α-180)/2]
Para os significados dos símbolos na fórmula, consultar a Figura 3.
4. Cálculo do desenvolvimento de cones circulares rectos oblíquos
O desenho de desenvolvimento do cone circular oblíquo direito é um arco de sector irregular. A fórmula de cálculo para o desenho de desenvolvimento do cone circular oblíquo direito mostrado na Figura 4 é
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[(A-D/2cosαn)2+(D/2)2pecado2αn+H2]
yn=fn(1-h/H)
m=Dsin(180°/n )
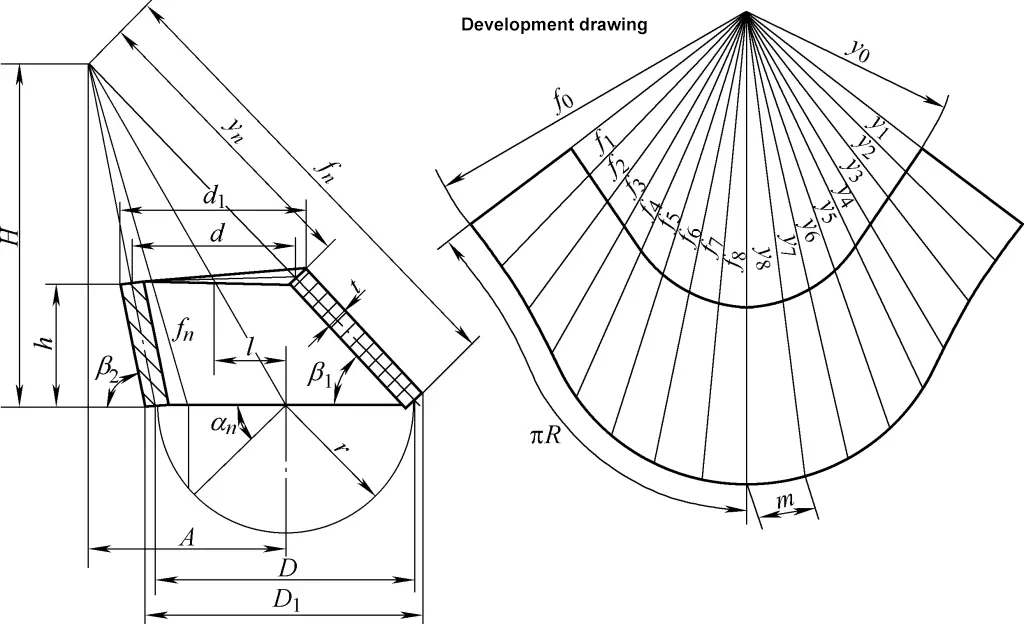
Na fórmula
- D1, d1 - Diâmetros exteriores das extremidades grande e pequena (mm);
- D, d - Diâmetros centrais das extremidades grande e pequena (mm);
- h - Altura central (mm);
- l - Distância excêntrica (mm);
- n - Número de divisões à volta da circunferência; quanto maior for o número de divisões, mais complexo é o cálculo mas mais exato é o desenho. Geralmente, o número de divisões pode ser consultado na Tabela 1;
- fn, yn - Comprimentos das linhas oblíquas do cone circular oblíquo direito (mm).
Quadro 1 Número de divisões para desenvolvimentos de chapa metálica
| Raio da peça desenvolvida/mm | Número de divisões |
| Dentro de 50 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| Mais de 2000 | 96 |
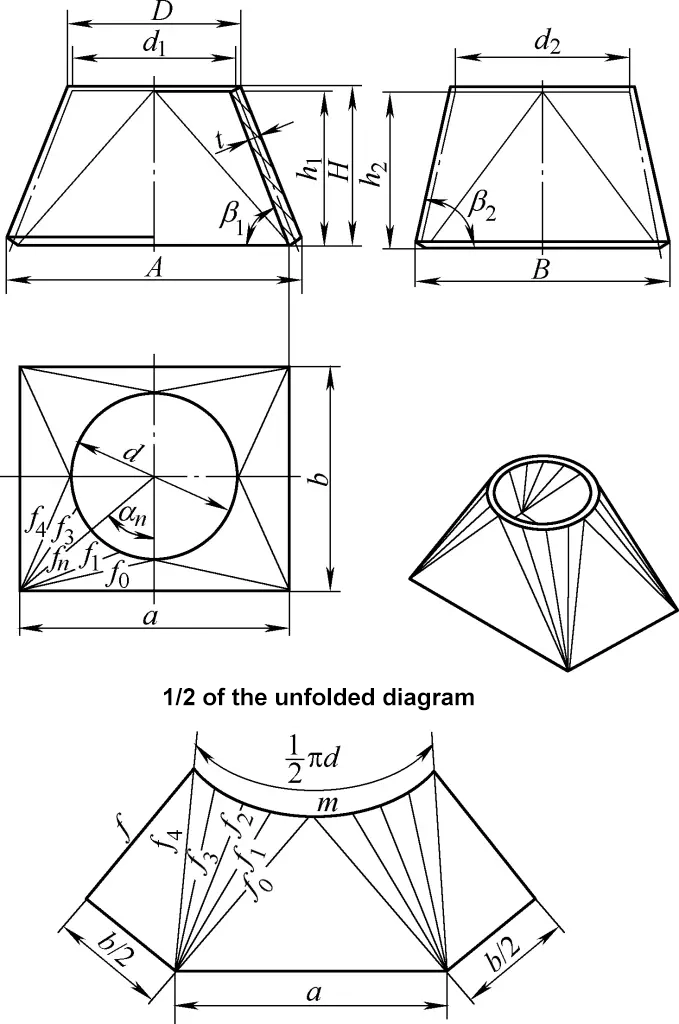
5. Cálculo do desenvolvimento da conduta de transição retangular-redonda ortocónica
A conduta ortocónica de transição de retangular para redondo representada na Figura 5 é constituída por quatro superfícies cónicas circulares rectas oblíquas iguais e quatro planos triangulares simétricos. A fórmula de cálculo para o seu desenho de desenvolvimento é
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(quando 0<α<90°)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(quando α=90°)
f=1/2√[(a-d)2+4h12]
m=πd/n
Para os significados dos símbolos na fórmula, consultar a Figura 5, e n é o número de divisões à volta da circunferência. Geralmente, o número de divisões no Quadro 1 pode satisfazer os requisitos de cálculo.