Durante el proceso de creación del plano de desarrollo del componente de chapa metálica, también es necesario tener en cuenta el impacto del grosor del material de procesamiento, es decir, realizar los ajustes adecuados del grosor de la chapa.
En general, para las chapas con un grosor inferior a 3 mm, no es necesario ajustar el grosor de la chapa. Puede calcularse según el diámetro central de la chapa o según las líneas de corte de las superficies interior y exterior. Las dimensiones después del conformado están dentro del rango de desviación permitido. Cuando el espesor de la chapa es superior a 3 mm, debe calcularse según el diámetro central de la chapa. Para facilitar la descripción, los cálculos para los siguientes materiales desarrollados se refieren al diámetro central del material de la chapa.
1. Cálculo del desarrollo de cáscaras cilíndricas
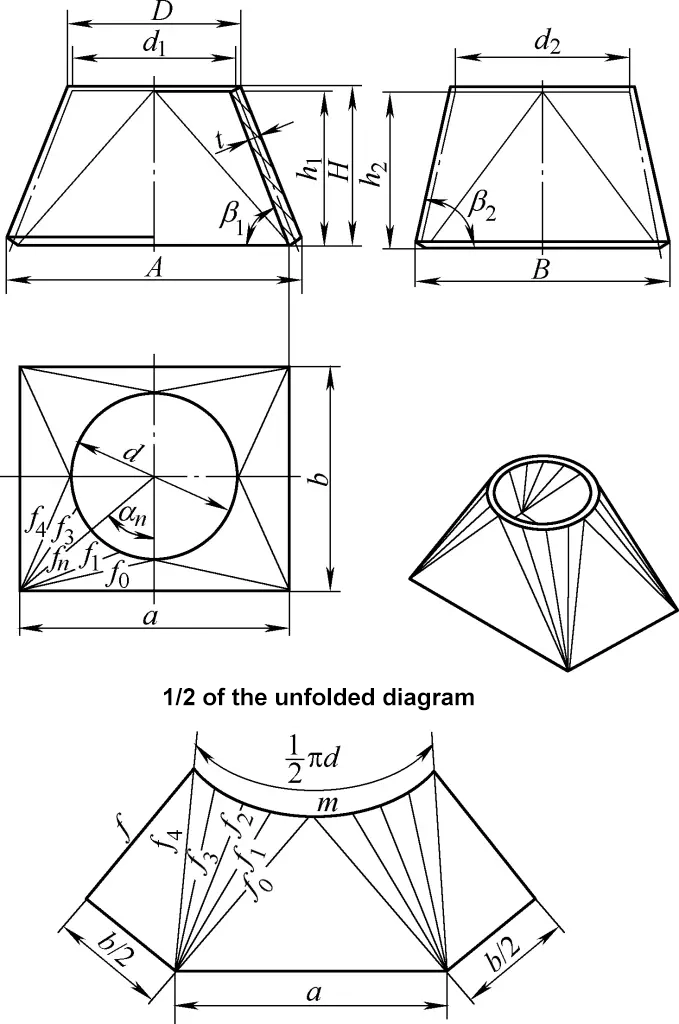
La envolvente cilíndrica pertenece a la superficie cilíndrica, y su dibujo de desarrollo es un rectángulo. Un lado del rectángulo es igual a la circunferencia del cilindro π(d-t), y el otro lado es la altura h del cilindro, como se muestra en la figura 1. En la figura, d es el diámetro exterior del cilindro y t es el espesor de la chapa.
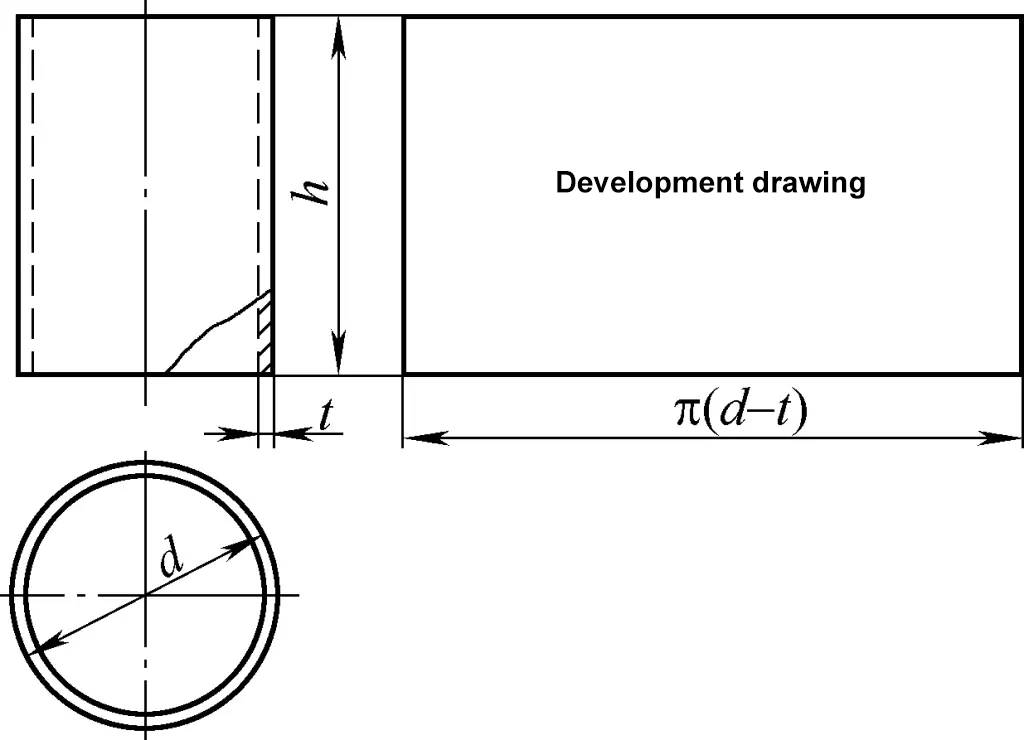
2. Cálculo del desarrollo de conos circulares rectos
El dibujo de desarrollo del cono circular derecho es un arco de sector. La fórmula de cálculo para el dibujo de desarrollo del cono circular derecho mostrado en la Figura 2 es:
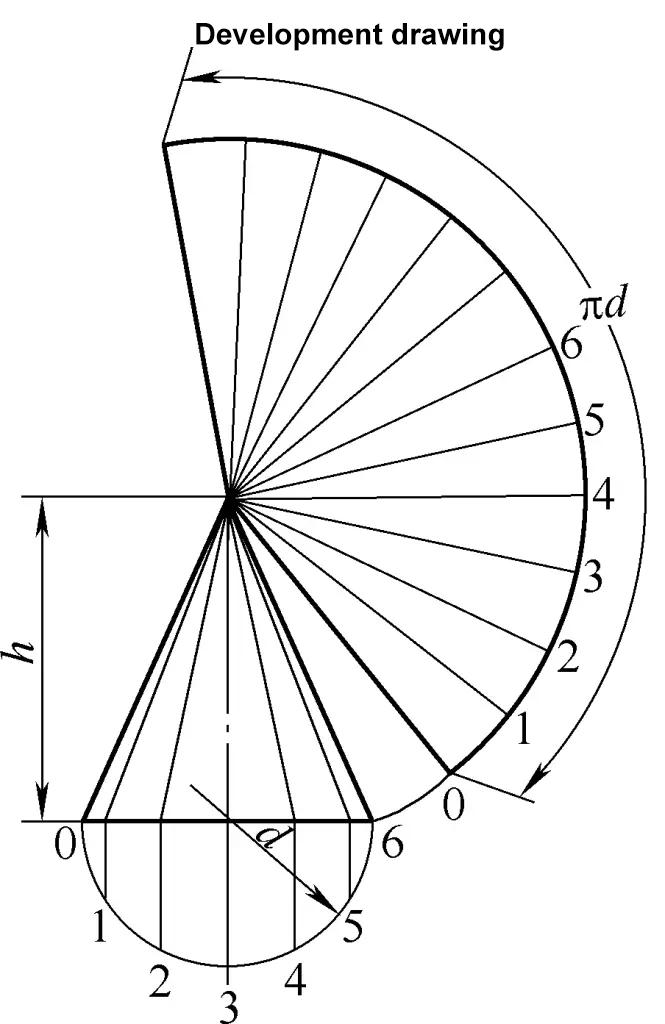
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
En la fórmula
- R - Radio del arco del sector (mm);
- α - Ángulo del sector (°);
- L - Longitud de cuerda del arco del sector (mm).
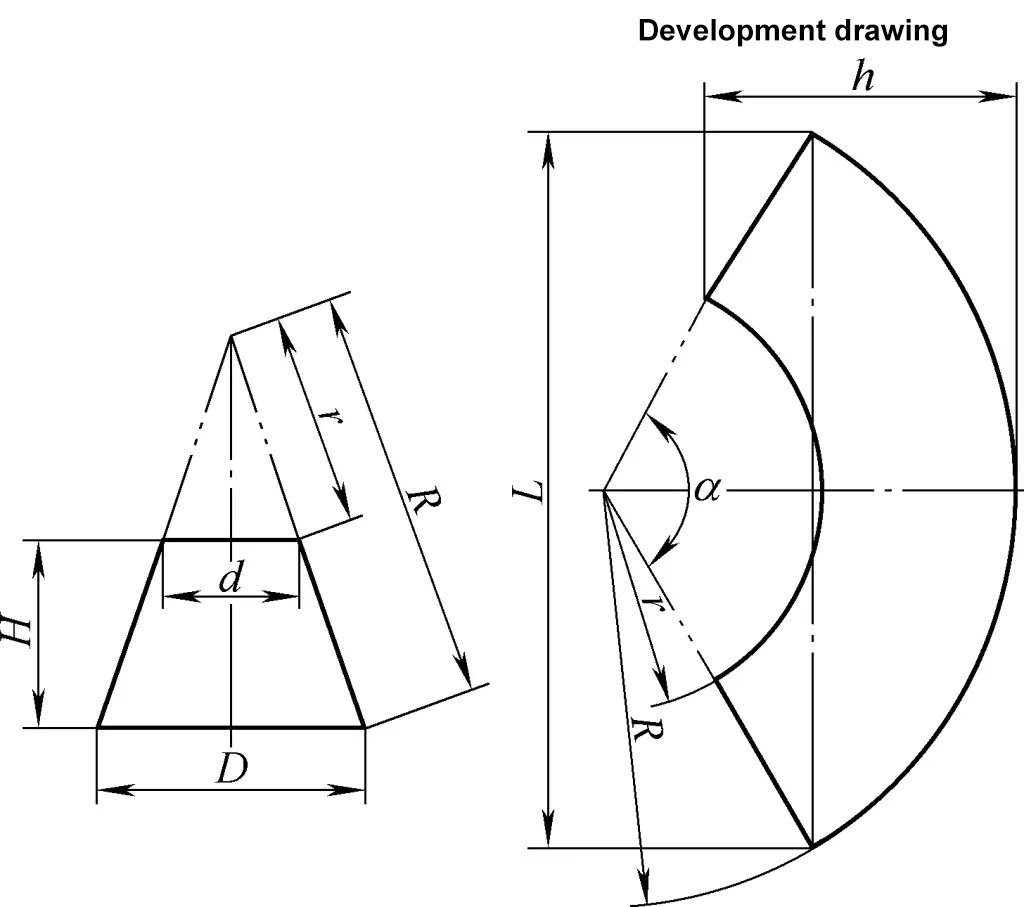
3. Cálculo del desarrollo de conos circulares rectos truncados
El dibujo de desarrollo del cono circular recto truncado es un arco de sector concéntrico. La fórmula de cálculo para el dibujo de desarrollo del cono circular derecho truncado que se muestra en la figura 3 es:
R=√{(D/2)2+[DH/(D-d)]2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
Cuando α>180°, h=R+rsin[(α-180)/2]
Para conocer el significado de los símbolos de la fórmula, véase la figura 3.
4. Cálculo del desarrollo de conos circulares rectos oblicuos
El dibujo de desarrollo del cono circular oblicuo recto es un arco de sector irregular. La fórmula de cálculo para el dibujo de desarrollo del cono circular oblicuo derecho mostrado en la figura 4 es:
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[(A-D/2cosαn)2+(D/2)2sin2αn+H2]
yn=fn(1-h/H)
m=Dsin(180°/n )
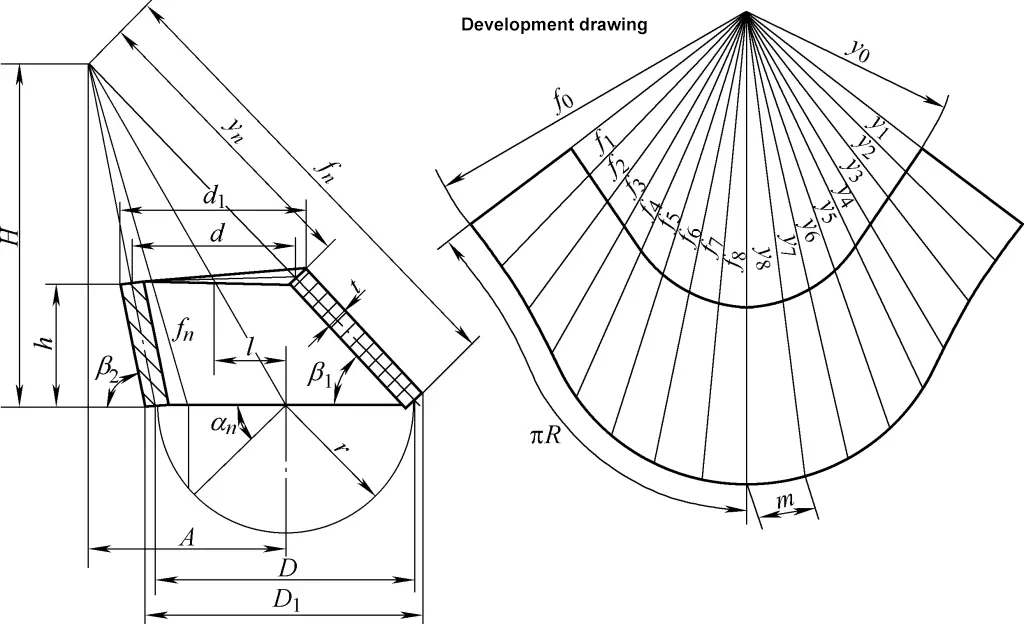
En la fórmula
- D1, d1 - Diámetros exteriores de los extremos grande y pequeño (mm);
- D, d - Diámetros centrales de los extremos grande y pequeño (mm);
- h - Altura central (mm);
- l - Distancia excéntrica (mm);
- n - Número de divisiones alrededor de la circunferencia; cuanto mayor sea el número de divisiones, más complejo será el cálculo pero más preciso será el dibujo. En general, el número de divisiones puede referenciarse en la Tabla 1;
- fn, yn - Longitudes de las líneas oblicuas del cono circular recto oblicuo (mm).
Cuadro 1 Número de divisiones para desarrollos de chapa metálica
| Radio de la pieza desarrollada/mm | Número de divisiones |
| Dentro del 50 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| Más de 2000 | 96 |
5. Cálculo del Desarrollo del Conducto de Transición Ortocónico Rectangular a Redondo
El conducto ortocónico de transición de rectangular a redondo que se muestra en la figura 5 consta de cuatro superficies cónicas circulares derechas oblicuas iguales y cuatro planos triangulares simétricos. La fórmula de cálculo para su dibujo de desarrollo es
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(cuando 0<α<90°)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(cuando α=90°)
f=1/2√[(a-d)2+4h12]
m=πd/n
Para conocer el significado de los símbolos de la fórmula, consulte la Figura 5, y n es el número de divisiones alrededor de la circunferencia. En general, el número de divisiones de la Tabla 1 puede satisfacer los requisitos de cálculo.