I. Von Drehern üblicherweise verwendete Präzisionsmesswerkzeuge und -instrumente
Präzisionsmessungen sollten unter konstanten Temperaturbedingungen durchgeführt werden. Die Temperatur des Raums mit konstanter Temperatur wird in der Regel auf (20±1)°C geregelt, mit einer Luftfeuchtigkeit von weniger als 65%. Der Raum sollte sauber, staubfrei und gut beleuchtet sein und mit Präzisionsmessgeräten, großen und kleinen Präzisionsplatten sowie üblichen Messwerkzeugen und Instrumenten ausgestattet sein.
In der mechanischen Fertigung werden zur Messung der Abmessungen von Werkstücken Messwerkzeuge, Messgeräte und Messvorrichtungen verwendet. Alle Messwerkzeuge, Messgeräte (Zähler) und Messvorrichtungen, die direkt oder indirekt den Wert des Messobjekts messen können, werden als Messgeräte bezeichnet.
Als Messwerkzeuge werden Messgeräte bezeichnet, die Werte in einer festen Form wiedergeben. Messgeräte (Zähler) bezeichnen Messgeräte, die die gemessene Größe in direkt beobachtbare Anzeigewerte oder gleichwertige Informationen umwandeln.
Im Folgenden werden die Messprinzipien und -methoden einiger Präzisionsmesswerkzeuge und -geräte vorgestellt, die in Fabriken häufig verwendet werden.
1. Messuhr
Eine Messuhr ist ein Messgerät mit Zeiger, das häufig bei Dreharbeiten eingesetzt wird. Sie kann zur Messung von Form- und Lagefehlern von Werkstücken verwendet werden, aber auch zur Messung von Werkstückabmessungen im Vergleichsverfahren. Es gibt zwei Arten von Messuhren: Messuhren und Hebelmessuhren.
(1) Messuhr (auch bekannt als Messuhr)
Die Messuhr und ihr Konstruktionsprinzip sind in Abbildung 1 dargestellt. Sie nutzt die Übertragung zwischen Zahnrädern und Zahnstangen, um die mikrolineare Verschiebung des Messstabs in die Winkelverschiebung des Zeigers umzuwandeln. Die Skalenwerte liegen bei 0,001 mm und 0,002 mm.
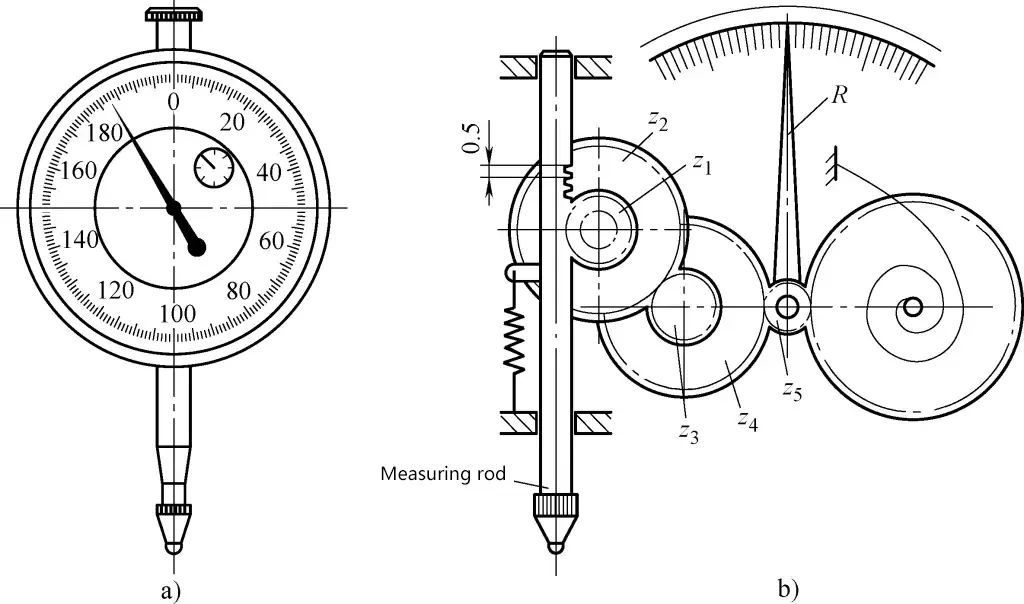
a) Außenansicht
b) Schema des Konstruktionsprinzips
Das Übertragungssystem der Messuhr besteht aus einer Zahnstange, einem Zahnradgetriebe und zwei Zahnradpaaren. Der Zahnstangenabstand auf der Messstange beträgt P=0,5mm, z1 =40, z2 =120, z3 =16, z4 =160, z5 =12. Wenn sich der Messstab linear um eine Strecke a=0,2mm bewegt, ist die Anzahl der Umdrehungen n des langen Zeigers
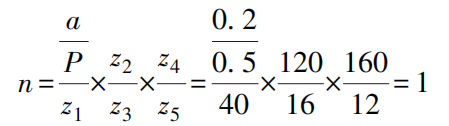
Das Zifferblatt ist in 200 Teilstriche unterteilt, und der Wert b, der durch jeden Teilstrich dargestellt wird, ist
b=0,2mm/200=0,001mm
Der Zweck der Spiralfeder ist die Beseitigung von Fehlern, die durch das Eingriffsspiel der Zahnradübertragung verursacht werden, und die Messkraft wird durch eine Zugfeder erzeugt.
(2) Hebelmessuhr
Die Hebelmessuhr mit einem Skalenwert von 0,002 mm und ihr Konstruktionsprinzip sind in Abbildung 2 dargestellt. Wenn der kugelförmige Messstab 7 nach links schwingt, drückt der Kipphebel 6 den zylindrischen Stift C auf das Sektorenrad 5, wodurch sich das Sektorenrad 5 gegen den Uhrzeigersinn um die Achse B dreht, wobei der zylindrische Stift D aus dem Kipphebel 6 ausrastet.
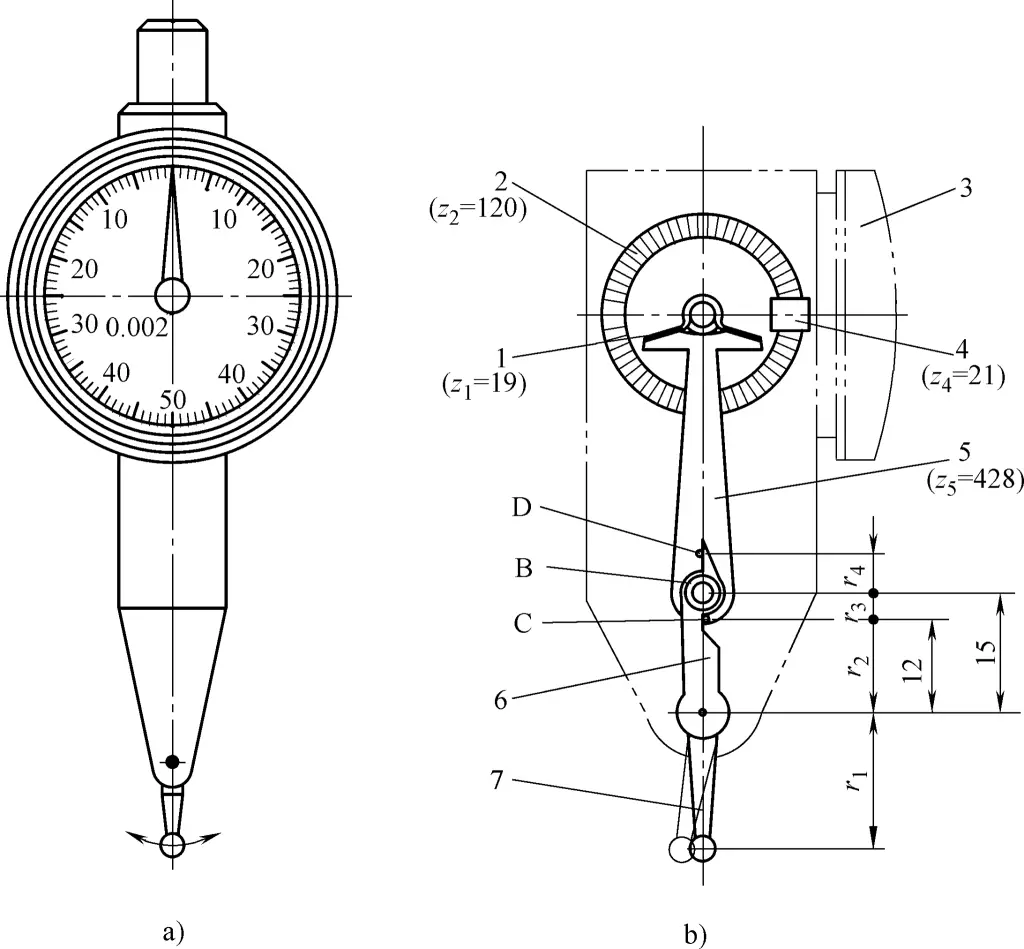
a) Außenansicht
b) Grundsatzdiagramm
1, 4-Kleine Gänge
2-Face-Getriebe
3-Zeiger
5-Sektoren-Getriebe
6-Schwenkarm
7-Kugelmessstab
Wenn der kugelförmige Messstab 7 nach rechts schwingt, drückt der Kipphebel 6 den zylindrischen Stift D auf das Sektorenrad 5, wodurch sich das Sektorenrad 5 ebenfalls gegen den Uhrzeigersinn um die Achse B dreht, wobei der zylindrische Stift C aus dem Kipphebel 6 ausrastet.
Unabhängig davon, ob der kugelförmige Messstab 7 nach links oder rechts schwingt, dreht sich das Sektorenrad 5 immer gegen den Uhrzeigersinn um die Achse B. Das Sektorenrad 5 treibt dann das kleine Zahnrad 1 und das koaxiale Stirnrad 2 an, das über das kleine Zahnrad 4 den Zeiger 3 dazu bringt, den Wert auf der Skala anzuzeigen.
Wie in Abbildung 2b gezeigt, ist bei r1 =16,39mm, r2 =12mm, r3 =3mm, r4 =5mm, z1 =19, z2 =120, z4 =21, z5 =428. Wenn sich der kugelförmige Messstab 7 um 0,2 mm nach links bewegt, beträgt die Anzahl der Umdrehungen n des Zeigers 3
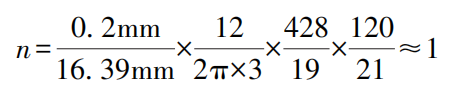
Wenn sich der kugelförmige Messstab 7 um 0,2 mm nach rechts bewegt, beträgt die Anzahl der Umdrehungen n des Zeigers 3
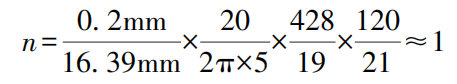
Das Zifferblatt ist in 100 Teilstriche unterteilt, und der durch jeden Teilstrich dargestellte Messwert b ist
b=0,2mm/100=0,002mm
Erfahrung des Skill Masters:
1) Bei der Verwendung einer Messuhr zur Messung sollte die Achse des Messstabs der Messuhr senkrecht zur Oberfläche des zu messenden Werkstücks stehen, da sonst Messfehler auftreten. Abbildung 3 zeigt die richtige Messmethode, bei der der Winkel zwischen der Messstabachse und der gemessenen Oberfläche des Werkstücks korrekt ist.
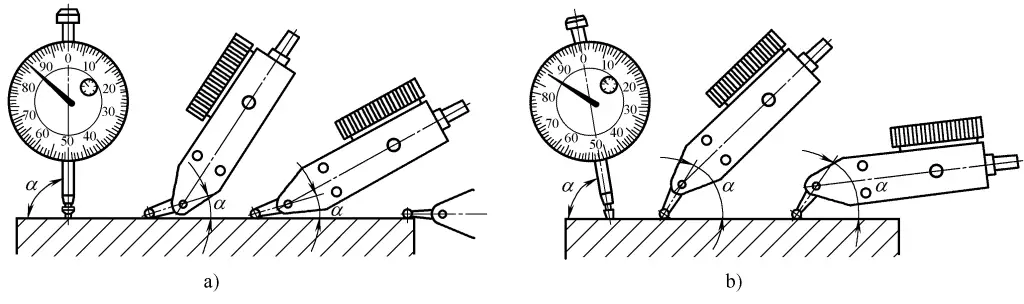
a) Korrektes Messverfahren
b) Falsche Messmethode
2) Bei Verwendung einer Hebelmessuhr ist der Fehler umso kleiner, je kleiner der Winkel zwischen der Messstabachse und der gemessenen Werkstückoberfläche ist. Wenn der Winkel α aufgrund der Messanforderungen nicht klein eingestellt werden kann (wenn α>15°), sollten die Messergebnisse korrigiert werden.
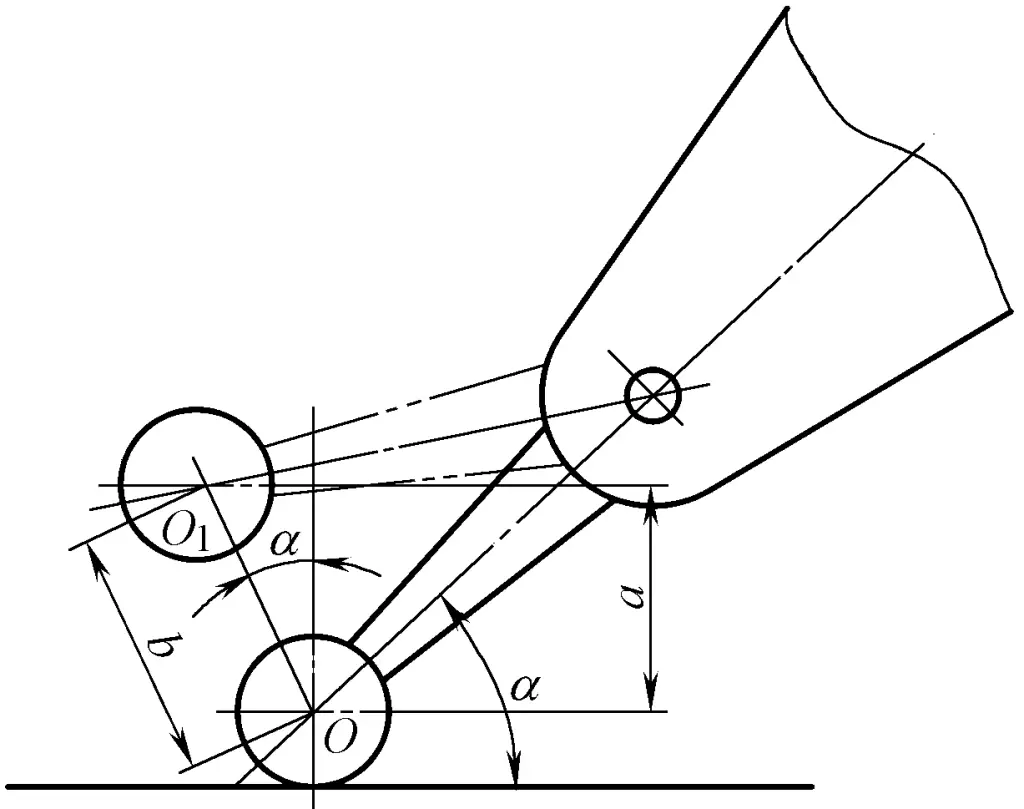
Wie in Abbildung 4 dargestellt, schwingt die Hebelmessuhr um eine Strecke b, die der Anzeige der Hebelmessuhr entspricht, wenn sich die Ebene um eine Strecke a hebt. Da b>a ist, erhöht sich der angezeigte Wert.
a=bcosα
Wo
a - Abstand, um den die Ebene ansteigt (mm);
b - Abstand, um den die Hebelmessuhr ausschlägt (mm);
α - Winkel zwischen der Messstabachse der Hebelmessuhr und der Messfläche (°).
3) Bei Verwendung einer Messuhr sollte diese sicher befestigt sein, um Vibrationen zu vermeiden; der Messkopf sollte das Messobjekt nicht plötzlich berühren; die Messuhr richtig einstellen; den Messbereich der Messuhr nicht überschreiten; keine Werkstücke mit relativ rauen Oberflächen messen.
4) Verhindern Sie, dass Wasser, Öl oder andere Flüssigkeiten in den Indikator eindringen oder auf den Messstab gelangen, da dies leicht zu Messfehlern führen kann.
5) Messuhren sollten nicht in der Nähe von Magnetfeldern platziert oder verwendet werden, um Genauigkeitsverluste durch Magnetisierung der Komponenten zu vermeiden.
2. Hebelmikrometer
Die Bügelmessschraube (Abbildung 5) ist ein Präzisionsmessgerät, das sich aus der Kausche einer Bügelmessschraube und dem Vergrößerungsteil eines Hebelgetriebes zusammensetzt. Sie hat eine hohe Präzision und wird hauptsächlich für präzise Messungen verwendet. Es hat Skalenwerte von 0,001 mm und 0,002 mm. Es kann sowohl für vergleichende als auch für absolute Messungen verwendet werden.
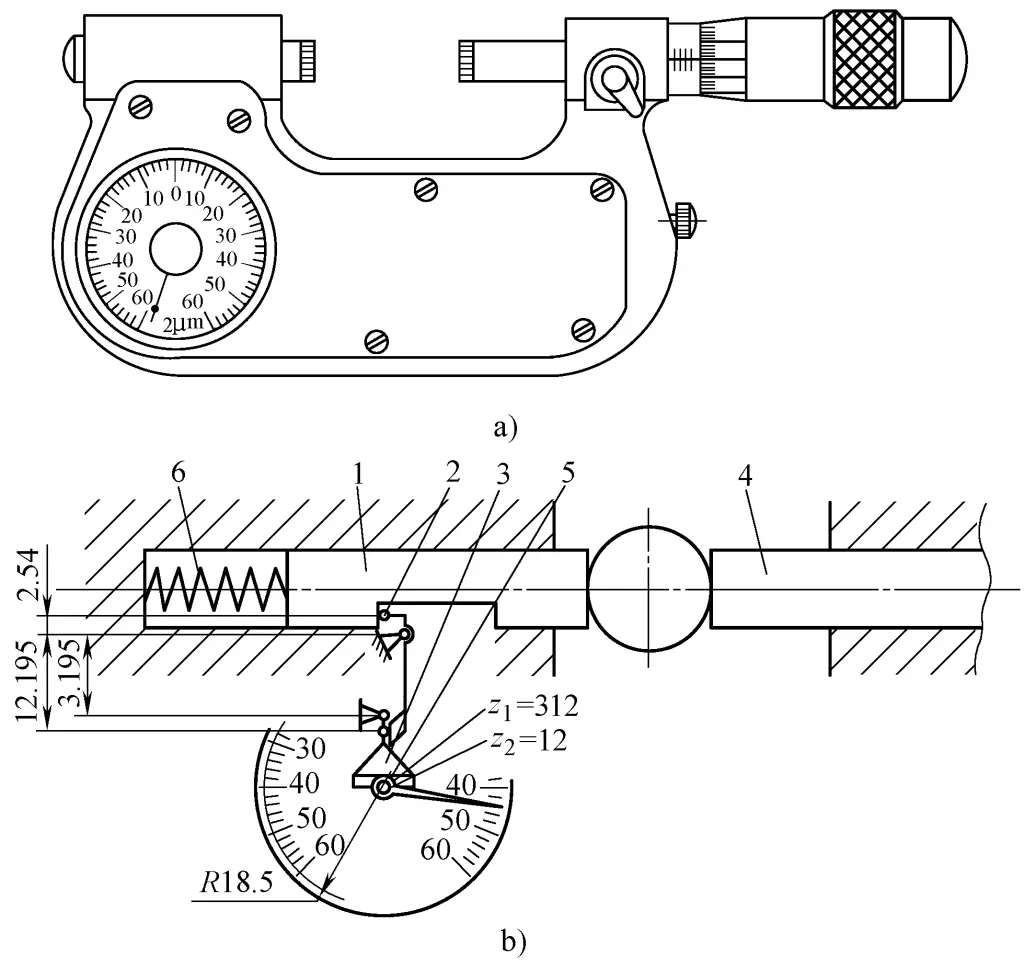
a) Außenansicht
b) Grundsatzdiagramm
1-Beweglicher Amboss
2-Hebel
3-Sektoren-Getriebe
4-Beweglicher Messstab
5-Kleines Getriebe
6-Drückerfeder
Das Funktionsprinzip der Hebelmessschraube ist in Abbildung 5b dargestellt. Wenn sich der bewegliche Amboss 1 bewegt, wird der Zeiger über den Hebel 2, das Sektorenrad 3 und das kleine Zahnrad 5, die auf der gleichen Achse montiert sind, in Drehung versetzt und zeigt die Bewegung des beweglichen Ambosses 1 auf der Skala an. Die Spiralfeder beseitigt das Spiel in der Übertragungskette, und die Messkraft wird durch die Druckfeder 6 erzeugt.
Wenn die Länge des kurzen Armes des Hebels r1 =2,54 mm, die Länge des langen Hebelarms r2 =12,195mm, der Teilkreisradius des kleinen Zahnrads r3 =3,195mm, die Zeigerlänge R=18,5mm, die Anzahl der Zähne des kleinen Zahnrades z2 =12, die Anzahl der Zähne des Sektorenrads z1 =312, ist das Transmissionsvergrößerungsverhältnis k
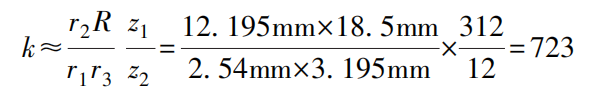
Das heißt, wenn sich der bewegliche Amboss 1 um a=0,002mm bewegt, dreht sich der Zeiger um eine Teilung mit einem Skalenwert b von
b≈ak=0.002mm×732=1.446mm
Erfahrung des Skill Masters:
1) Bei der Verwendung einer Hebelmikrometerschraube für Relativmessungen müssen Endmaße verwendet werden, um die Hebelmikrometerschraube entsprechend der Größe des gemessenen Werkstücks einzustellen. Beim Ablesen sollte der Fehler des Endmaßes oder des Endmaßsatzes berücksichtigt werden.
2) Wenn Sie ein Werkstück mit einer Hebelmikrometerschraube messen, drücken Sie zunächst den Rückzugsknopf, damit das Werkstück die Ambossfläche des Messstabs sanft berühren kann, ohne es zu erzwingen.
3) Vor der Messung sollte das Werkstück auf eine gusseiserne Platte gelegt werden, um Raumtemperatur zu erreichen; während der Messung sollte die Bedienung geschickt und schnell sein, um zu verhindern, dass Temperaturschwankungen die Messgenauigkeit beeinträchtigen.
4) Beim Messen des Durchmessers eines Werkstücks sollte der Messwert am Drehpunkt des Zeigers abgelesen werden.
3. Bügelmessgerät mit Hebel
Das Fühlhebelmessgerät ist ein Messwerkzeug, das nach dem Prinzip der Hebelübersetzung mit Skalenwerten von 0,002 mm und 0,005 mm arbeitet. Es kann mit Endmaßen für die relative Messung von Werkstücken verwendet werden und kann auch die Formfehler von Werkstücken messen.
Das Funktionsprinzip des Fühlhebelmessgeräts ist in Abbildung 1-76a dargestellt. Wenn sich der bewegliche Amboss 1 bewegt, treibt er den Zeiger 7 über den Hebel 2, das Sektorenrad 3 und das kleine Zahnrad 5, die auf derselben Achse montiert sind, zur Drehung an, wodurch die Bewegung des beweglichen Ambosses 1 auf der Skala 8 angezeigt wird.
Die Spiralfeder 6 beseitigt das Spiel in der Übertragungskette, und die Messkraft wird durch die Feder 10 erzeugt. Um den Verschleiß der Messflächen zu verringern und die Messung zu erleichtern, ist er mit einem Rückzugsknopf 9 ausgestattet. Die Außenansicht des Fühlhebelmessgeräts ist in Abbildung 6b dargestellt.
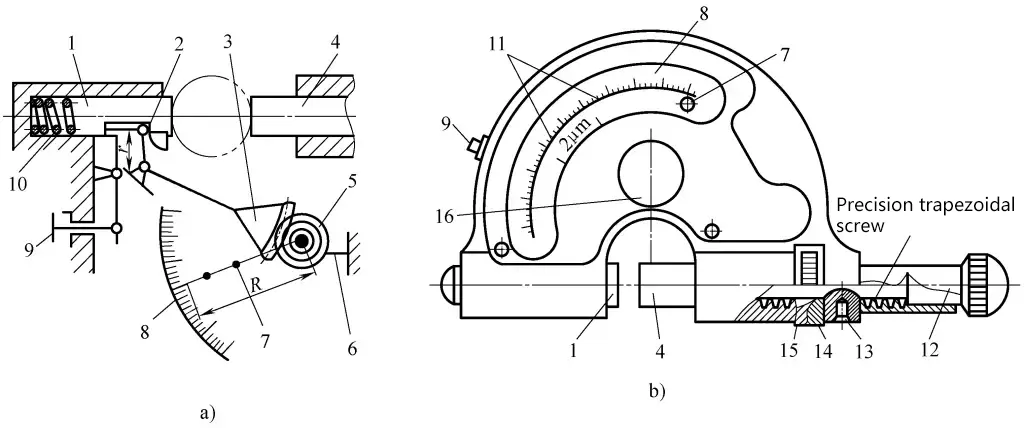
a) Schema des Arbeitsprinzips
b) Außenansicht
1-Beweglicher Amboss
2-Hebel
3-Sektoren-Getriebe
4-Verstellbarer Amboss
5-Kleines Getriebe
6-Haarfeder
7-Zeiger
8-Wahl
9-Tasten
10-Frühling
11-Toleranzanzeige
12-Ärmel
13-Schraube
14-Rändelmutter
15-Scheiben-Feder
16-Deckel
Vor der Messung wird zunächst die Hülse 12 gelöst, das Endmaß zwischen den beweglichen Amboss 1 und den verstellbaren Amboss 4 gelegt, dann die Rändelmutter 14 gedreht, um den Zeiger 7 auf die Nullposition der Skala auszurichten, und schließlich die Hülse 12 angezogen, um den verstellbaren Amboss 4 zu fixieren.
Die Tellerfeder 15 beseitigt das Spiel zwischen der Mutter und dem Trapezgewinde des verstellbaren Ambosses, und die Schraube 13 verhindert, dass sich der verstellbare Amboss dreht. Entfernen Sie die Abdeckung 16, um die Toleranzanzeige mit einem Spezialschlüssel einzustellen.
Die Länge des Hebels 2 ist r, die Länge des Zeigers 7 ist R, die Anzahl der Zähne des Zahnsektors 3 ist z1 ist die Anzahl der Zähne des kleinen Zahnrads 5 z2 Wenn sich der bewegliche Amboss 1 um eine Strecke a bewegt, ist die vom Zeiger 7 zurückgelegte Strecke b
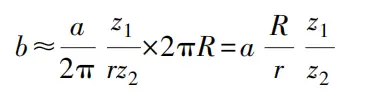
Deshalb
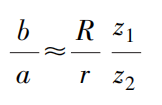
Wenn b/a das Vergrößerungsverhältnis ist und es gleich k ist, dann
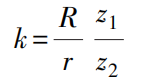
Je größer der Radius R des Zeigers 7 ist, desto mehr Zähne z1 auf dem Zahnradsektor 3, desto kleiner ist die Länge r des Hebels 2 und desto weniger Zähne z2 auf dem kleinen Zahnrad 5, desto größer ist das Vergrößerungsverhältnis k.
4. Sinusbalken
Ein Sinusbalken (auch Sinuslineal genannt) ist ein Messinstrument, das das Prinzip der Sinusfunktion für indirekte Messungen verwendet, wie in Abbildung 7 dargestellt.
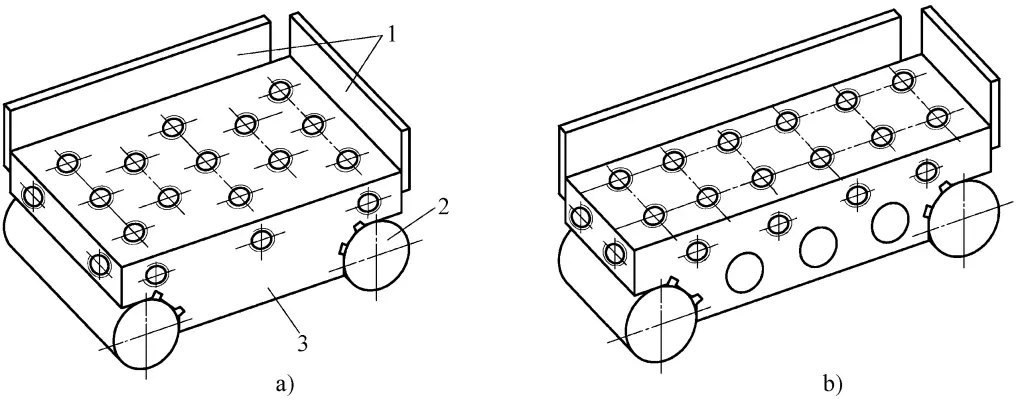
a) Breiter Typ
b) Schmaler Typ
1-Endplatte
2-Zylinder
3-Hauptteil
Der Sinusbalken besteht im Wesentlichen aus einer hochpräzisen Arbeitsebene und zwei Präzisionszylindern mit demselben Durchmesser. Die Achsen der beiden Zylinder sind parallel zueinander, und die Mittellinie, die sie verbindet, verläuft parallel zur Arbeitsfläche. Je nach Verwendungszweck werden sie in einen breiten Typ, einen schmalen Typ und einen Typ mit Mittelpunkten unterteilt.
Der Sinusbalken misst nach dem Prinzip der Sinusfunktion. Legen Sie bei der Verwendung Endmaße oder einen Satz Endmaße mit der Größe h unter einen Zylinder des Sinusbalkens, so dass die Arbeitsebene des Sinusbalkens einen Winkel α mit der Planscheibe bildet. Vergleichen Sie diesen Winkel mit dem Winkel des zu prüfenden Werkstücks.
Erfahrung des Skill Masters:
- Der Sinusbalken ist ein Präzisionsmessgerät, das vor dem Gebrauch gründlich gereinigt werden muss.
- Der Oberflächenrauhigkeitswert Ra des gemessenen Werkstücks sollte weniger als 1,6μm betragen; die Werkstückoberfläche sollte keine Grate oder Schmutz aufweisen und darf nicht magnetisch sein.
- Der Sinusbalken sollte behutsam gehandhabt werden, und es ist strengstens untersagt, ihn zu schlagen oder zu ziehen, um einen Verschleiß der Zylinder und eine Beeinträchtigung der Genauigkeit zu vermeiden.
- Nach dem Gebrauch sollte der Sinusbalken gründlich gereinigt, mit Rostschutzöl bestrichen und in einem speziellen Koffer aufbewahrt werden.
- Beim Auflegen des zu messenden Werkstücks auf den Sinusbalken ist der vordere oder seitliche Anschlag des Sinusbalkens zur Positionierung zu verwenden, um sicherzustellen, dass der Winkelquerschnitt des Werkstücks in der vertikalen Ebene der Zylinderachse des Sinusbalkens liegt, da es sonst zu Messfehlern kommt.
5. Komparator für Hebelgetriebe
Der Teilungswert des Hebelgetriebekomparators beträgt 0,001 mm, der Messbereich liegt bei ±0,05 mm, sein Bereich ist kleiner als der einer Messuhr, aber die Genauigkeit ist höher als die einer Messuhr. Der Hebelgetriebekomparator wird in der Regel auf einem speziellen Messständer für die Messung montiert, wie in Abbildung 8 dargestellt.
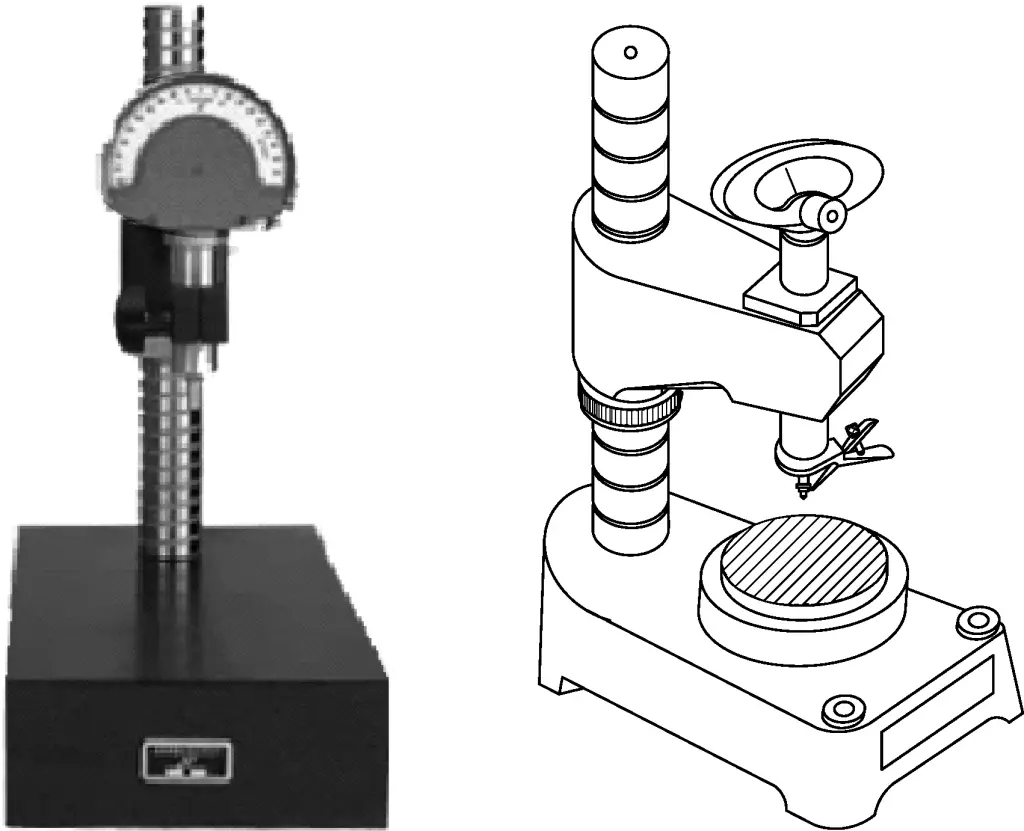
Bei der Messung wird die Größe der Endmaße als Standard verwendet, um die Abmessungen von Präzisionswerkstücken mit der Vergleichsmethode zu messen, und es können auch die Form- und Positionsfehler von Werkstücken gemessen werden.
Der Hebelgetriebe-Komparator ist in Abbildung 9 dargestellt. Wenn sich die Messstange 7 bewegt, wird der Zahnsektor 5 über den Hebel 6 in Drehung versetzt, und das kleine Zahnrad 4 dreht sich ebenfalls. Das zum kleinen Zahnrad 4 koaxiale Sektorrad 3 überträgt die Bewegung auf das kleine Zahnrad 2, und der Zeiger 1 zeigt den entsprechenden Wert auf der Skala an.
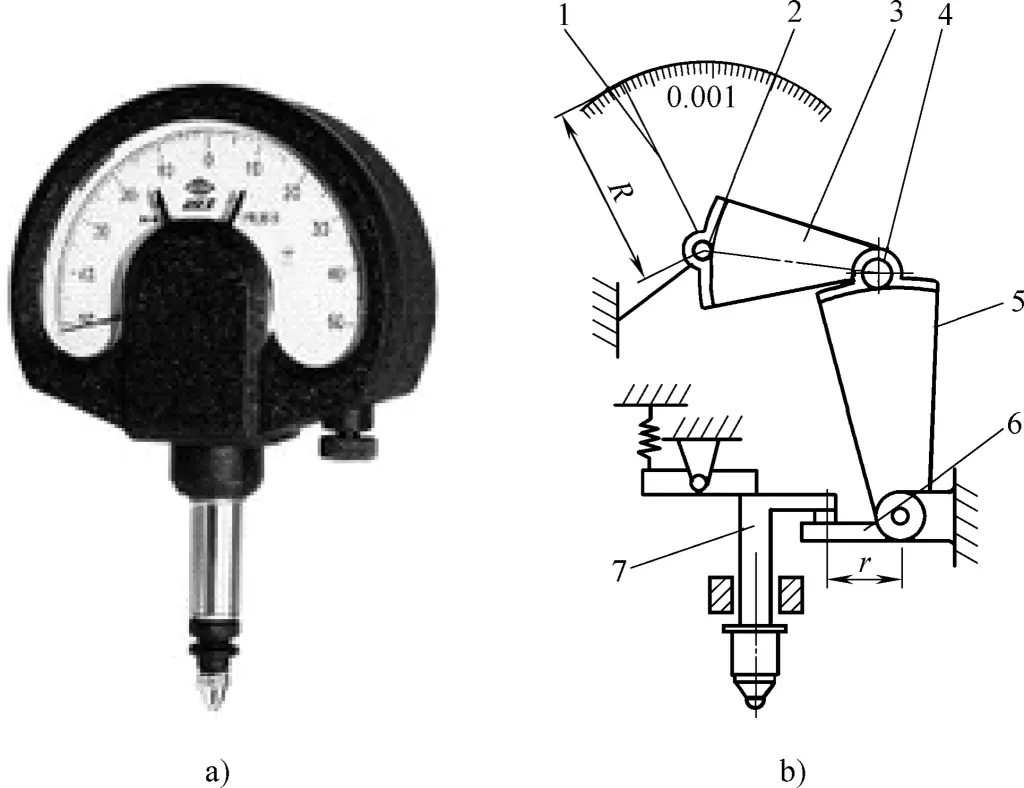
a) Außenansicht
b) Schematische Darstellung
1-Zeiger
2, 4-Kleine Gänge
3, 5-Sektoren-Getriebe
6-Hebel
7Messstab
Wenn die Armlänge des Hebels 6 r, die Länge des Zeigers 1 R und die Anzahl der Zähne der Zahnräder 2, 3, 4, 5 z sind2 , z3 , z4 , z5 beziehungsweise. Wenn sich der Messstab 7 um eine Strecke a bewegt, beträgt die Strecke b, um die sich der Zeiger 1 dreht
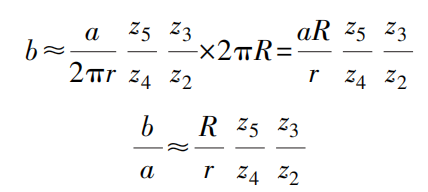
Wenn b/a als Vergrößerungsverhältnis bezeichnet wird und gleich k ist, dann
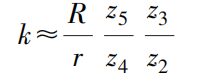
Bei r=4,52mm, R=24,5mm, z2 =18, z3 =180, z4 =28, z5 =400, ist das Vergrößerungsverhältnis k

Wenn sich der Messstab 7 um eine Strecke a=0,001 mm bewegt, beträgt die Strecke b, um die sich der Zeiger um eine Teilung dreht
b=ak=0.001mm×774=0.774mm
6. Torsionsfedermikrometer
Die Torsionsfedermessschraube verwendet eine Torsionsfeder als Übertragungsmechanismus für die Größenumrechnung und Vergrößerung. Ihr herausragendes Merkmal ist der einfache Aufbau, der große Vergrößerungsfaktor und das Fehlen von Reibung oder Spiel im Vergrößerungsmechanismus, wodurch die Messgenauigkeit und Empfindlichkeit verbessert werden. Die Außenansicht und das schematische Diagramm sind in Abbildung 10 dargestellt.
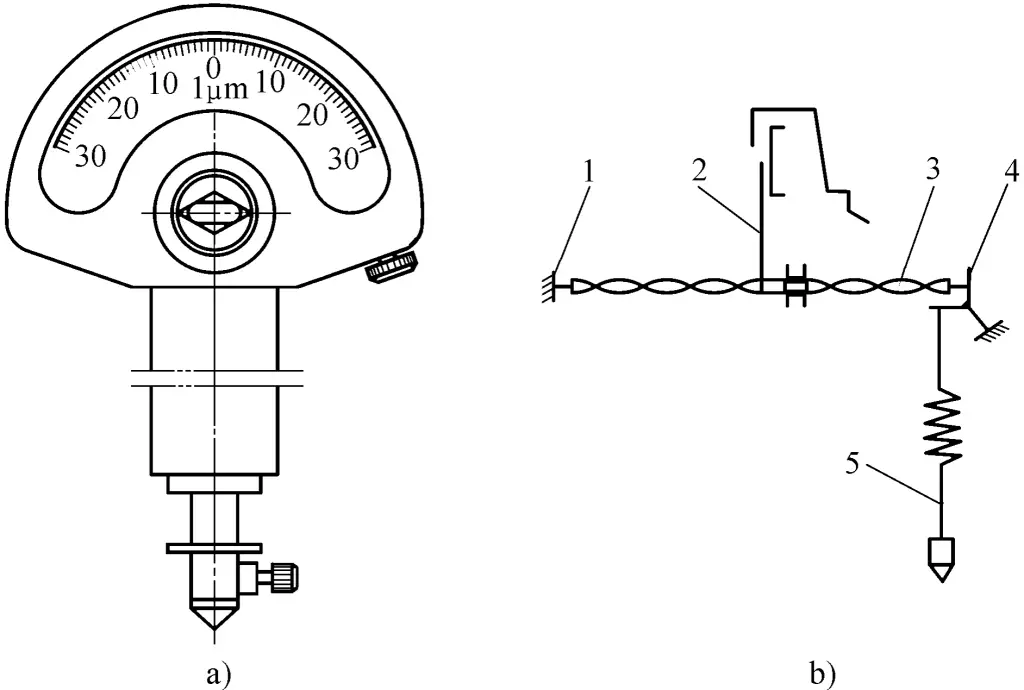
a) Außenansicht
b) Schematische Darstellung
1-Rahmen
2-Zeiger
3-Torsionsfederband
4-Federn-Brücke
5-Messstab
Das Torsionsfederband 3 ist ein Metallband aus Berylliumbronze mit rechteckigem Querschnitt (0,005 mm × 0,1 mm × 40 mm), das mit einem Ende am Rahmen 1 und mit dem anderen Ende an der Federbrücke 4 befestigt ist. In der Mitte der Torsionsfeder ist ein Zeiger 2 angebracht. Die Hälfte des Metallstreifens ist von der Mitte aus nach rechts verdreht, die andere Hälfte nach links. Wenn der Messstab 5 eine kleine Auslenkung nach oben erfährt, bewegt sich das obere Ende der Federbrücke 4 nach rechts, wodurch das Torsionsfederband 3 gedehnt wird und der Glasfaserzeiger 2, der sich in der Mitte des Torsionsfederbandes befindet, in einem Winkel ausschlägt, der die Auslenkung des Messstabs 5 anzeigt.
Die Messmethode der Schenkelfedermessschraube ist die gleiche wie die des Hebelradkomparators. Zusätzlich kann der Kopf der Schenkelfedermessschraube auf ein Stativ montiert werden, um verschiedene Messungen auf einer Plattform durchzuführen. Während der Messung sollte der Messkopf senkrecht zur Oberfläche des zu messenden Werkstücks stehen.
Erfahrung des Skill Masters:
1) Der Hebelgetriebekomparator und die Schenkelfedermessschraube sollten zunächst auf einem festen Messstativ installiert werden. Stellen Sie vor der Messung den Messtisch des Messstativs so ein, dass er senkrecht zur Achse der Messstange des Hebelradkomparators und der Schenkelfedermessschraube steht; stellen Sie dann die Säule des Messstativs so ein, dass der Messkopf den Endmaßblock oder das Werkstück leicht berührt.
2) Versuchen Sie, bei der Messung möglichst den mittleren Teil der Skala zu verwenden.
3) Die Struktur der Torsionsfedermessschraube ist empfindlich und der Messbereich ist klein. Stellen Sie den Kontaktabstand zwischen dem Messkopf und dem Werkstück sorgfältig ein; wechseln Sie den Messkopf rechtzeitig entsprechend der Form des Werkstücks.
4) Der Oberflächenrauhigkeitswert Ra des gemessenen Werkstücks sollte weniger als 1,6μm betragen; die Werkstückoberfläche sollte keine Grate oder Schmutz aufweisen. Das Werkstück sollte vor der Messung auf eine gusseiserne Platte gelegt und auf Raumtemperatur gebracht werden; während der Messung sollte die Bedienung geschickt und schnell sein, um zu verhindern, dass Temperaturschwankungen die Messgenauigkeit beeinträchtigen.
7. Parallelendmaße
Endmaße sind hochpräzise Messwerkzeuge, deren Arbeitslänge durch den Abstand zwischen zwei parallelen Messflächen bestimmt wird. Sie werden hauptsächlich für die Übertragung von Längenbezugsmaßen verwendet, wie in Abbildung 11 dargestellt. Endmaße können auch zur Überprüfung von Messgeräten, zur Einstellung der Nullposition von Geräten bei Relativmessungen und zur Einstellung von Präzisionswerkzeugmaschinen verwendet werden.

Parallelendmaße sind rechteckige Prismen mit rechteckigem Querschnitt aus Chrom-Mangan-Stahl, Nickel-Chrom-Stahl oder Wälzlagerstahl. Sie haben zwei parallele, hochpräzise Arbeitsflächen mit geringer Oberflächenrauhigkeit. Jedes Endmaß ist mit einer Nenngröße gekennzeichnet, wie in Abbildung 12 dargestellt.
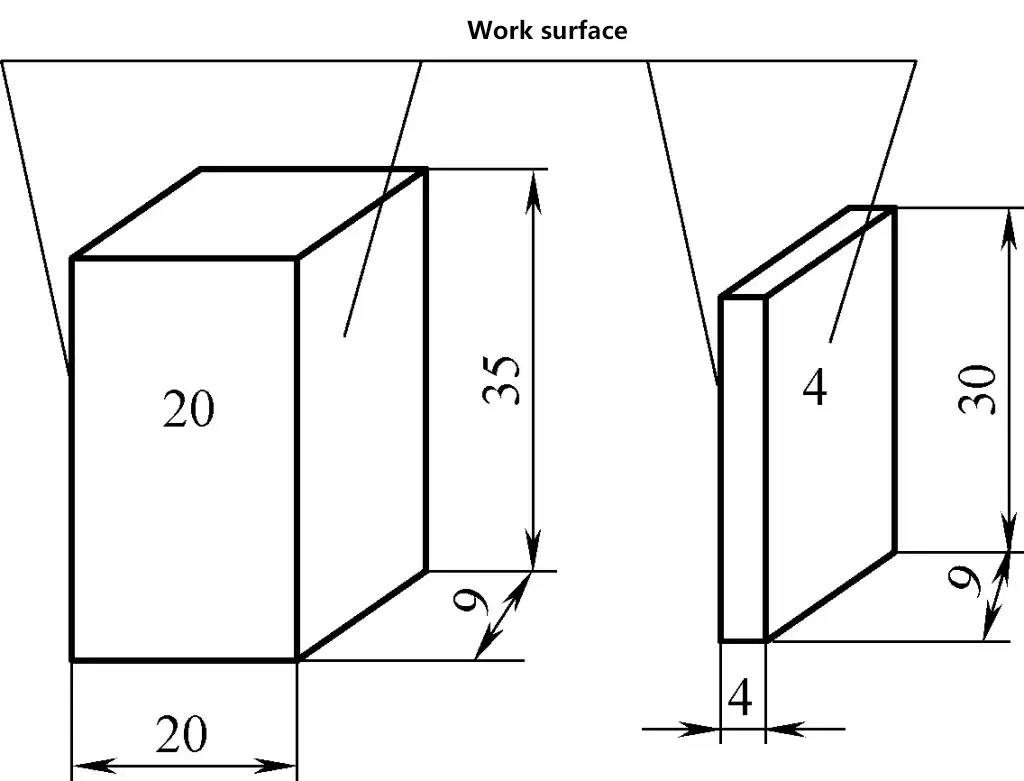
Die Fertigungspräzision von Endmaßen wird in sechs Stufen eingeteilt: 00, 0, 1, 2, 3 und K, wobei 00 die höchste und 3 die niedrigste Präzision darstellt, während K die Kalibrierstufe ist.
Die Hauptgrundlage für die Einteilung von Endmaßen in "Klassen" ist ihre Herstellungspräzision, die von der Grenzabweichung der Mittellänge des Endmaßes, der Toleranz der Längenabweichung und der Auswringfähigkeit abhängt. Bei der Verwendung nach Güteklassen wird direkt die auf dem Endmaß angegebene Nenngröße verwendet, was zwar praktisch ist, aber zu Herstellungsfehlern und damit zu weniger genauen Messergebnissen führt.
Endmaße werden nach ihrer Prüfgenauigkeit in sechs Klassen eingeteilt: 1, 2, 3, 4, 5 und 6, wobei 1 die höchste und 6 die niedrigste Prüfgenauigkeit darstellt. Die Hauptgrundlage für die Einteilung der Endmaße in "Klassen" ist ihre Prüfgenauigkeit, die von der Grenzabweichung der Mittellänge des Endmaßes, der Toleranz der Planparallelität und der Auswringfähigkeit abhängt. Bei der Verwendung nach Klassen wird die tatsächliche Größe des geeichten Endmaßes verwendet, was zu einer höheren Messgenauigkeit führt.
Endmaße werden in Sätzen verwendet und können zu verschiedenen Größen kombiniert werden. Wenn die Arbeitsfläche eines Endmaßes auf der Arbeitsfläche eines anderen Endmaßes gleitet, können sie mit leichtem Handdruck aneinander haften. Daher können mehrere Endmaße je nach Bedarf zu einem Endmaßsatz kombiniert werden.
Wenn Sie Endmaße zu einer bestimmten Größe kombinieren, verwenden Sie so wenig Endmaße wie möglich, um die gewünschte Größe zu erreichen, im Allgemeinen nicht mehr als vier Endmaße. Beginnen Sie bei der Auswahl der Endmaße mit der letzten Ziffer der gewünschten Kombinationsgröße und wählen Sie Endmaße aus, die die Anzahl der Ziffern bei jeder Auswahl um eine Ziffer verringern, usw.
Ein Beispiel: Um einen Endmaßsatz von 38,935 mm mit einem Satz von 83 Endmaßen zu bilden, ist die Auswahlmethode wie folgt:

Erfahrung des Skill Masters:
1) Endmaße sind nur zur Überprüfung von Messgeräten, zur Durchführung von Präzisionsmessungen und zur Einstellung von Präzisionswerkzeugmaschinen zulässig.
2) Bevor Sie Endmaße verwenden, überprüfen Sie sorgfältig das Aussehen der Endmaße und die gemessene Oberfläche des Werkstücks. Magnetische Werkstücke sollten vor der Verwendung von Endmaßen entmagnetisiert werden.
3) Vor dem Kombinieren von Endmaßsätzen reinigen Sie die Endmaße mit säurefreiem Flugbenzin, wasserfreiem Ethanol oder reinem Benzol, wischen Sie die Endmaße mit feinem, weichem Fensterleder, entfetteter Baumwolle, Leinen oder Seide ab und verwenden Sie dann die Methode des parallelen Auswringens oder des Kreuzwringens für die Kombination.
4) Nach dem Gebrauch sind die Endmaße unverzüglich zu demontieren, zu reinigen und abzuwischen, mit Rostschutzöl zu versehen und in die dafür vorgesehene Position im Spezialkoffer zu legen.
5) Prüfen Sie die Endmaße regelmäßig und bewahren Sie die Prüfbescheinigung im Koffer auf.
8. Wasserwaage
Eine Wasserwaage ist ein häufig verwendetes Messwerkzeug zur Messung kleiner Neigungswinkel einer Werkstückoberfläche gegenüber der Horizontalen. Sie wird hauptsächlich zum Messen von Geradheits- und Rechtwinkligkeitsfehlern verwendet und kann beim Einstellen und Installieren von Geräten in horizontale oder vertikale Positionen eingesetzt werden.
(1) Rahmen-Wasserwaage
Eine Rahmenwasserwaage ist in Abbildung 13 dargestellt. Die Messfläche des Rahmens hat sowohl eine ebene Fläche als auch eine V-Nut, wobei die V-Nut die Messung auf zylindrischen Flächen erleichtert.
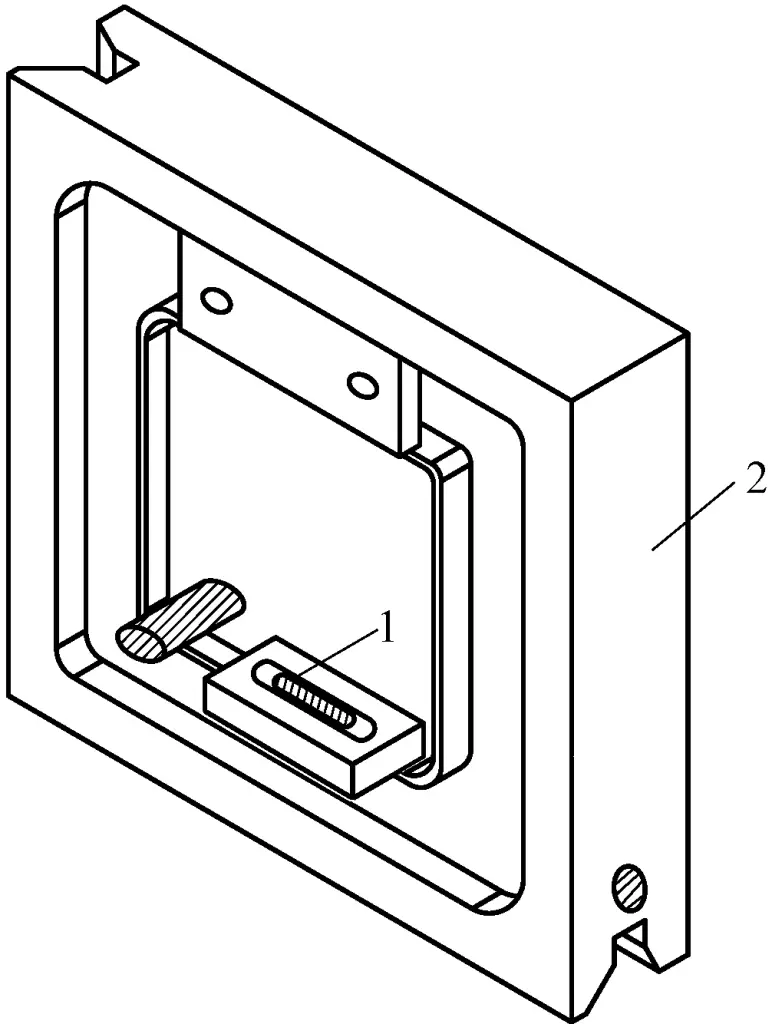
1-Hauptpegel-Fläschchen
2-Hauptteil
Die Libelle ist ein verschlossenes Glasröhrchen mit einem bestimmten Krümmungsradius, das auf der Oberfläche mit Skalen versehen ist, mit Äther gefüllt ist und eine Luftblase enthält. Die Blase bleibt immer an der höchsten Stelle des Glasrohrs. Wird die Wasserwaage in einem Winkel geneigt, bewegt sich die Blase nach links oder rechts, und der Geradheits- oder Rechtwinkligkeitsfehler kann anhand der zurückgelegten Strecke berechnet werden.
Das Funktionsprinzip der Wasserwaage ist in Abbildung 14 dargestellt. Bei einer Wasserwaage mit einem Teilungswert von 0,02mm/1000mm hat die Hauptlibelle der Wasserwaage einen Krümmungsradius R=103132mm. Wenn die Ebene über eine Länge von 1000 mm um 0,02 mm geneigt ist, beträgt der Neigungswinkel θ
tanθ=0.02mm/1000mm=0.00002
θ=4"
Der Winkel, um den sich die Blase dreht, ist gleich dem Winkel, um den sich die Ebene dreht. Die Strecke, die die Blase für 1 Teilung zurücklegt, ist
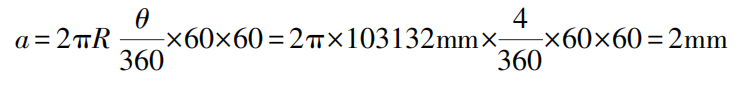
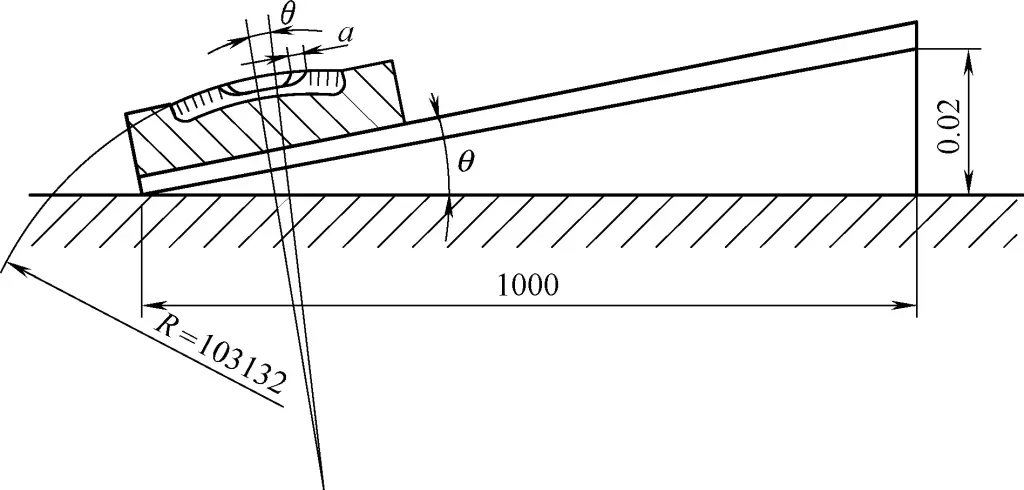
Das heißt, dass bei einer Wasserwaage mit einem Teilungswert von 0,002 mm/1000 mm der Abstand zwischen den einzelnen Teilstrichen auf dem Glasrohr 2 mm beträgt. Daraus wird ersichtlich, dass die Wasserwaage ein Messinstrument ist, das nach dem Prinzip des gleichen Drehwinkels und des vergrößerten Krümmungsradius funktioniert.
(2) Koinzidenz-Wasserwaage
Eine Koinzidenz-Wasserwaage ist ein kleines Winkelmessgerät mit relativ hoher Messgenauigkeit, großem Messbereich und praktischer Tragbarkeit, wie in Abbildung 15 dargestellt. Die Blase in der Libelle 7 wird gleichzeitig an beiden Halbkanten durch das Koinzidenzprisma 8 im Sichtfeld der Visierlupe 1 abgebildet.
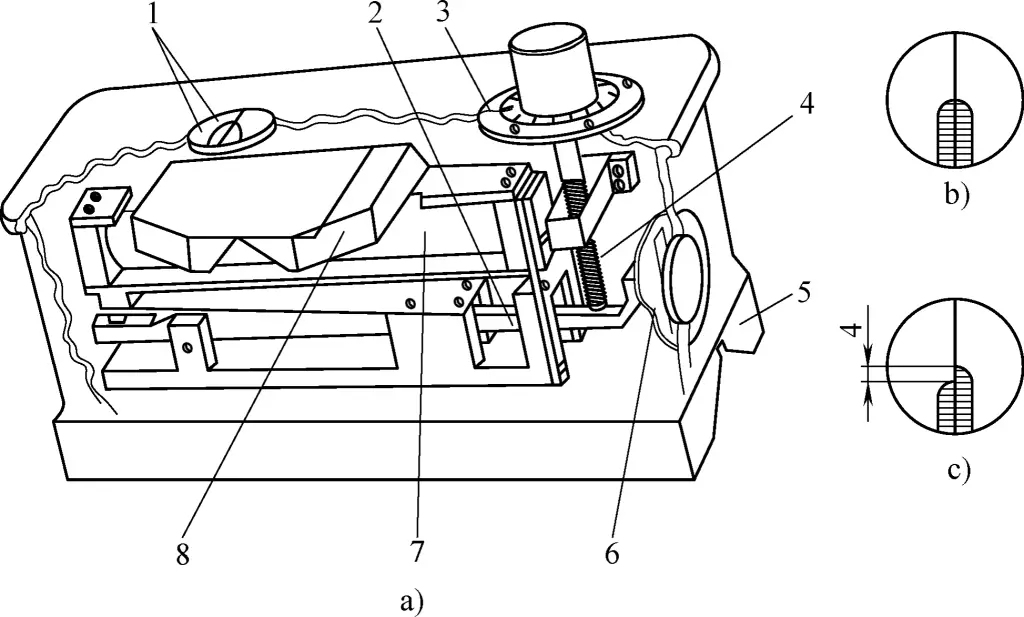
1-Sichtlupe
2-Hebel
3-Graduiertes Zifferblatt
4-Mikrometer-Schraube
5-Basis
6-Skala
7-Geistesstufe
8-Koinzidenzprisma
Legen Sie die Wasserwaage bei der Verwendung auf das zu messende Werkstück. Wenn sie in einem bestimmten Winkel geneigt wird, kann man durch die Visierlupe 1 sehen, dass die beiden Halbkanten des Bildes mit einem Versatz zusammenkommen. Drehen Sie die Mikrometerschraube 4 mit der Hand und benutzen Sie den Hebel 2, um die Wasserwaage 7 leicht zu drehen, bis die Bilder der Blasenränder zu einem glatten, halbkreisförmigen Kopf verschmelzen.
Der ganzzahlige Teil des Wertes wird von der Skala 6 abgelesen, der dezimale Teil von der Skala 3. Wenn die Skala zum Beispiel 1 mm anzeigt und das Zifferblatt sich gedreht hat
Bei 16 Teilungen beträgt der Wert 1,16 mm, was einen Höhenunterschied von 1,16 mm pro 1 m Länge bedeutet.
II. Gemeinsame Methoden zur Messung von Abmessungen
Die Bearbeitungsqualität von Teilen umfasst die Bearbeitungsgenauigkeit und die Oberflächenqualität. Zur Bearbeitungsgenauigkeit gehören Maßgenauigkeit, Formgenauigkeit und Positionsgenauigkeit. Zu den Indikatoren für die Oberflächenqualität gehören die Oberflächenrauhigkeit, der Grad der Oberflächenverfestigung sowie die Art und das Ausmaß der Eigenspannung. Hier werden vor allem die Maßgenauigkeit und deren Prüfung sowie die Form- und Lagegenauigkeit und deren Prüfung vorgestellt.
Die Maßgenauigkeit bezieht sich auf den Grad der Übereinstimmung zwischen den tatsächlichen und den idealen Bauteilabmessungen, d. h. den Grad der Maßhaltigkeit, der durch Maßtoleranzen (als Toleranzen bezeichnet) kontrolliert wird.
Höhere Toleranzklassen haben kleinere Toleranzwerte und eine höhere Genauigkeit; umgekehrt führen größere Toleranzwerte zu einer geringeren Genauigkeit. Bei Teilen mit demselben Nennmaß bestimmt die Größe des Toleranzwertes die Genauigkeit des Teils. Kleinere Toleranzwerte bedeuten höhere Genauigkeit, größere Toleranzwerte bedeuten geringere Genauigkeit.
In der mechanischen Fertigungsindustrie gibt es zwei Hauptkategorien von Instrumenten, die zum Messen oder Prüfen von Werkstückabmessungen verwendet werden: Messwerkzeuge und Messgeräte (auch als Messvorrichtungen bezeichnet). Bei Messwerkzeugen handelt es sich um einfache Messgeräte, die die Grenzwerte von Längeneinheiten direkt darstellen können, wie z. B. Stahlmaßstäbe, Messschieber, Mikrometer, Endmaße, Lehrdorne und Bügelmessgeräte.
Messgeräte sind Instrumente zur Vergrößerung oder Unterteilung der Länge nach mechanischen, optischen, pneumatischen oder elektrischen Prinzipien, wie z. B. Messuhren, Mikrometer, Torsionsmikrometer und Wasserwaagen. Wenn bei der Verwendung dieser Instrumente zur Prüfung das gemessene Maß zwischen dem oberen und dem unteren Grenzmaß liegt, gilt das Teil als zulässig.
Ist die gemessene Abmessung größer als die maximale Materialgröße, ist das Teil inakzeptabel und muss weiter bearbeitet werden. Ist die gemessene Abmessung kleiner als die minimale Materialgröße, wird das Teil verschrottet.
1. Prüfung von Innen- und Außendurchmesser, Länge, Tiefe und Rillenbreite
(1) Messung des Außendurchmessers.
Bei der Messung von Außendurchmessern werden für Standard-Präzisionsmaße in der Regel Messschieber und Rachenlehren verwendet, während für höhere Präzisionsanforderungen Mikrometer und andere Präzisionsmessgeräte gewählt werden. Typen von Außenmikrometern sind in Abbildung 16 dargestellt.

a) Standard-Außenmikrometer
b) Außenmikrometer mit Hebel
c) Digitale Bügelmessschraube
d) Dreirillige Bügelmessschraube
e) Punktmikrometer
f) Wanddickenmikrometer
(2) Messung des Innendurchmessers.
Bei der Messung von Lochdurchmessern sollten je nach Größe, Menge und Präzisionsanforderungen des Werkstücks geeignete Messwerkzeuge ausgewählt werden. Für geringere Genauigkeitsanforderungen können Stahllineale, Innenmessschieber, Lehrdorne oder Messschieber verwendet werden. Für höhere Genauigkeitsanforderungen können Innenmikrometer, Innenmessschrauben oder Bohrungsmessgeräte verwendet werden. Abbildung 17 zeigt gängige Messwerkzeuge für Innendurchmesser.

a) Innenmikrometer
b) Glatter zylindrischer Lehrdorn
c) Bohrungsmessgerät
d) Interner Schnappmesser
e) Innenmikrometer
(3) Messung von Länge, Tiefe und Rillenbreite.
Die Länge bezieht sich im Allgemeinen auf die Abmessungen von Außenflächen, z. B. den Abstand von einer Stufenfläche zu einer bestimmten Endfläche. Wenn die Anforderungen an die Maßgenauigkeit nicht hoch sind, können Stahllineale, Schablonen, Messschieber oder Tiefenmessgeräte für die Messung verwendet werden. Übliche Messwerkzeuge sind in Abbildung 18 dargestellt. Ist eine höhere Maßgenauigkeit erforderlich, kann das Werkstück auf eine Prüfplatte gelegt werden, und Messuhren oder Fühlhebelmessgeräte und Endmaße können für Vergleichsmessungen verwendet werden.

a) Tiefenmikrometer
b) Tiefenmessgerät mit Nonius
c) Messschieber
2. Methoden zur Überprüfung des konischen Kegels
(1) Überprüfung der Konizität mit einem Universal-Fasenwinkelmesser.
Bei winkligen Teilen oder konischen Oberflächen mit geringeren Genauigkeitsanforderungen kann ein Universal-Fasenwinkelmesser zur Überprüfung der Konizität verwendet werden, wie in Abbildung 19 dargestellt.
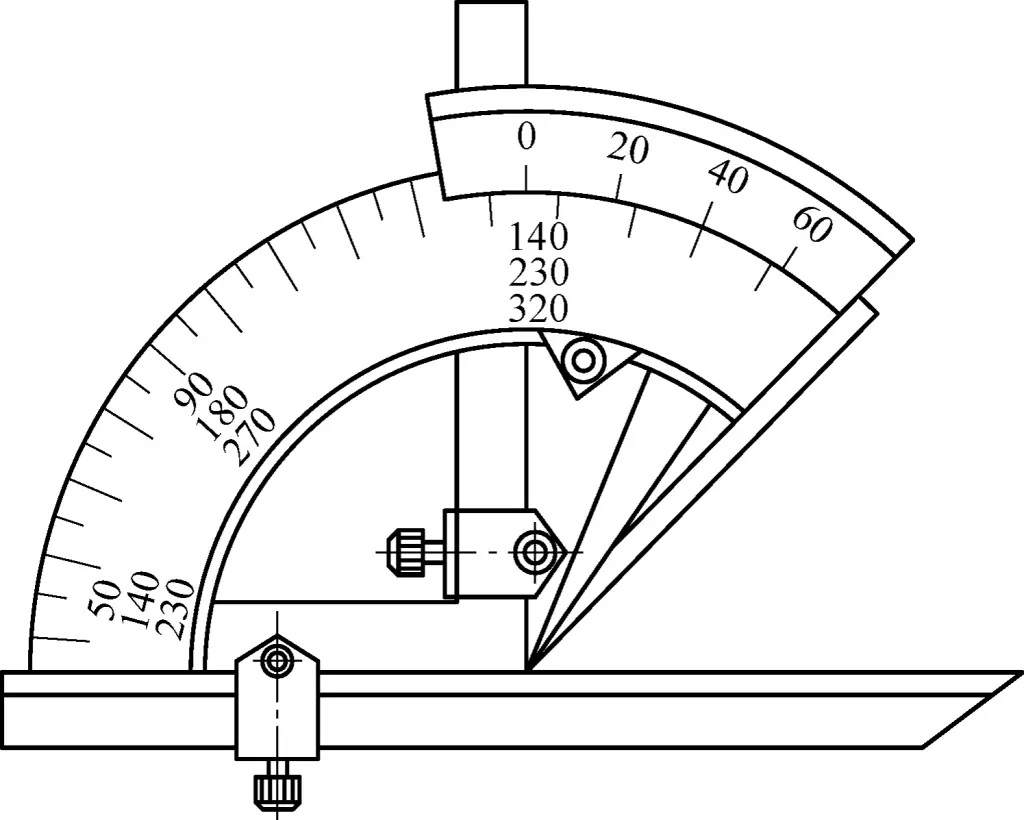
Stellen Sie zunächst den Universal-Fasenwinkelmesser auf den zu messenden Winkelbereich ein. Richten Sie die Winkelseite des Winkelmessers auf die Stirnfläche des Werkstücks aus (durch die Werkstückmitte), und lassen Sie das Stahllineal die schräge Fläche des Werkstücks berühren. Verwenden Sie die Lichttransmissionsmethode, um den Winkel zu messen.
Erfahrung des Skill Masters:
Entfernen Sie vor der Messung Grate vom Werkstück und halten Sie die Oberflächen des Werkstücks und des Messwerkzeugs sauber. Die Messfläche des Winkelmessers muss durch die mittlere Symmetrieebene des Werkstücks gehen und die Grundfläche muss mit der Bezugsfläche des Werkstücks übereinstimmen. Ziehen Sie beim Ablesen zuerst die Befestigungsschraube des Universal-Fasenmessers an und entfernen Sie ihn dann vom Werkstück, um Winkeländerungen zu vermeiden, die Messfehler verursachen könnten.
(2) Prüfung von Kegel und Abmessungen mit einem Kegelmessgerät.
Tragen Sie zunächst mit der Einfärbemethode drei dünne, gleichmäßige Linien aus vorbereiteter Mennige oder blauer Tinte entlang der Mantellinie des Werkstücks über dessen gesamte Länge auf. Setzen Sie dann die Lehre vorsichtig auf das Werkstück und richten Sie sie wiederholt aus. Beachten Sie, dass der Drehbereich innerhalb einer halben Umdrehung liegen sollte.
Entfernen Sie die Lehre und beobachten Sie die "gedruckten" roten Bleispuren auf der konischen Oberfläche des Werkstücks, um die Genauigkeit der Verjüngung zu beurteilen. Verwenden Sie die Gut- und Schlechtpunktlinien des Messgeräts, um die konischen Abmessungen zu bestimmen, wie in Abbildung 20 dargestellt.
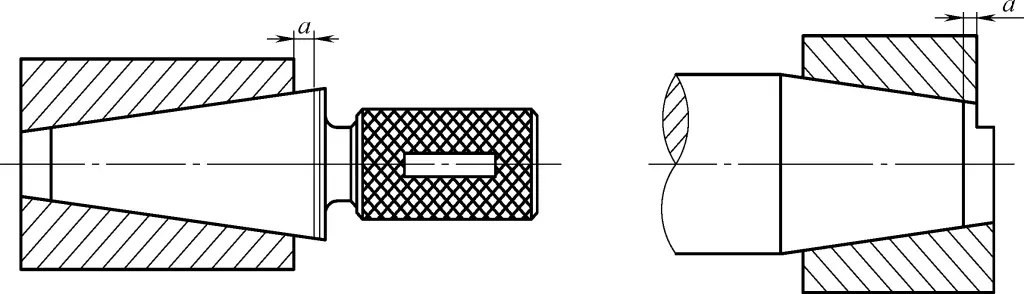
(3) Überprüfung der Konizität mit einem Sinusbalken.
Legen Sie bei der Prüfung den Sinusbalken auf eine Präzisionsplatte und das Werkstück auf den Arbeitstisch des Sinusbalkens. Legen Sie einen Satz Endmaße unter einen der Zylinder des Sinusbalkens. Die Höhe des Endmaßsatzes kann auf der Grundlage des konischen Winkels des zu messenden Werkstücks berechnet werden.
Prüfen Sie dann mit einer Messuhr (oder Mikrometer) die Höhe der beiden Enden der konischen Mantellinie des Werkstücks. Wenn die Höhen an beiden Enden gleich sind, bedeutet dies, dass der Winkel oder die Verjüngung des Werkstücks korrekt ist. Sind die Höhen an beiden Enden ungleich, bedeutet dies, dass der Winkel oder die Verjüngung des Werkstücks einen Fehler aufweist.
Sinusstäbe sind vielseitig einsetzbar und werden häufig zur Prüfung von Werkstückwinkeln und -verjüngungen verwendet.
Abbildung 21 zeigt die Messung eines Kegelwinkels mit einem Sinusbalken. Zunächst wird das Endmaß h entsprechend dem Nennwert α' des zu messenden Kegelwinkels berechnet und ein Standardwinkel α gebildet.
h=Lsinα
Wo
- L - Mittenabstand zwischen den beiden Zylindern des Sinusstabs (mm);
- α - Nennwert des Kegelwinkels des Werkstücks (°).
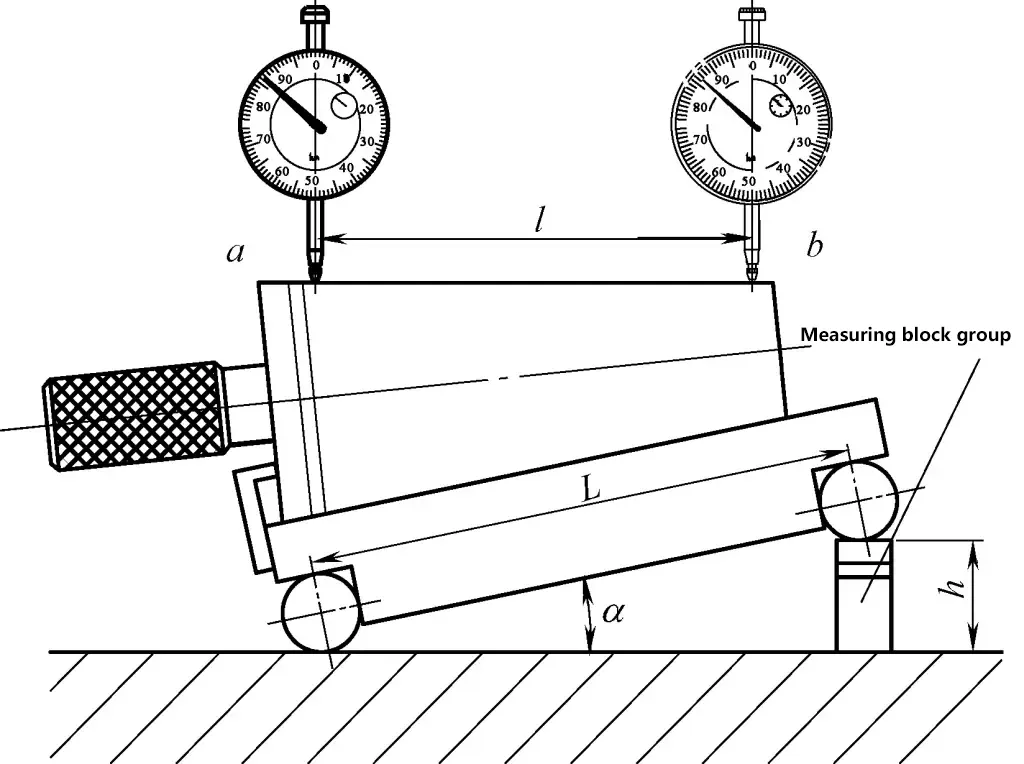
Legen Sie den Sinusbalken auf eine Platte, wobei ein Zylinder die Platte berührt. Ein Endmaß mit dem Maß h wird unter den anderen Zylinder gelegt, wobei die Hauptarbeitsebene des Sinusbalkens gegenüber der Platte um einen Standardwinkel α geneigt wird.
Nach dem Aufsetzen des konischen Werkstücks messen Sie mit einer Messschraube die Punkte a und b auf der oberen Mantellinie des gemessenen Kegels (der Abstand zwischen den Punkten a und b ist l). Die Messwerte an den Punkten a und b sind r₀ bzw. r₁. Wenn r₀ ≠ r₁, bedeutet dies, dass ein Kegelfehler zwischen dem Kegelwinkel des gemessenen Werkstücks und dem Standardwinkel α besteht. Die Formel zur Berechnung des Kegelfehlers lautet:
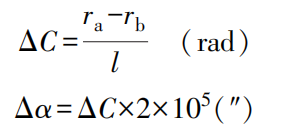
Wo
- ΔC - Kegelfehler (rad);
- Δα - Konischer Winkelfehler (");
- r₀ - Ablesung am Punkt b des Kegels (mm);
- r₁ - Ablesung am Punkt a des Kegels (mm).
Mit 1rad = 57,3° ≈ (2×10⁵)" als Umrechnungsfaktor von Bogenmaß in Sekunden erhält man den Fehler ΔC des gemessenen Kegelwinkels (α).
Beispiel: Ein Sinusbalken mit einem Achsabstand L=200mm wird zur Messung eines Morsekegels Nr. 4 mit einem nominalen Kegelwinkel von 2°58'30.6″ (2.975179°) verwendet. Die Messung wird wie in Abbildung 1-91 gezeigt durchgeführt. Wenn der Abstand zwischen den Messpunkten a und b l=80mm beträgt und r₀ - r₁ = 0,01mm, berechnen Sie den Kegelfehler und den tatsächlichen Kegelwinkel dieses Kegellehrdorns.
Lösung: Gegeben L=200mm, l=80mm, dann
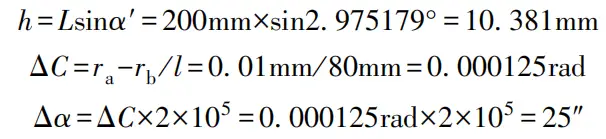
Da r₀ - r₁ = 0,01 mm ist, ist Punkt a höher als Punkt b, der tatsächliche Kegelwinkel ist größer als der nominale Kegelwinkel.
αreal =α’+Δα=2°58’30.6″+25″=2°58’55.6″
3. Prüfung der Exzentrizität
(1) Wenn die Genauigkeitsanforderung für die Exzentrizität e nicht hoch ist, verwenden Sie einen Messschieber, um den Mindestabstand a zwischen den beiden zylindrischen Oberflächen zu messen, und berechnen Sie dann die Exzentrizität e anhand der folgenden Formel:
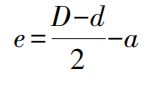
(2) Wenn eine höhere Genauigkeit für die Exzentrizität e erforderlich ist, verwenden Sie die folgende Prüfmethode: Messen Sie die Exzentrizität e genau mit einer Messuhr, wie in Abbildung 22 dargestellt.
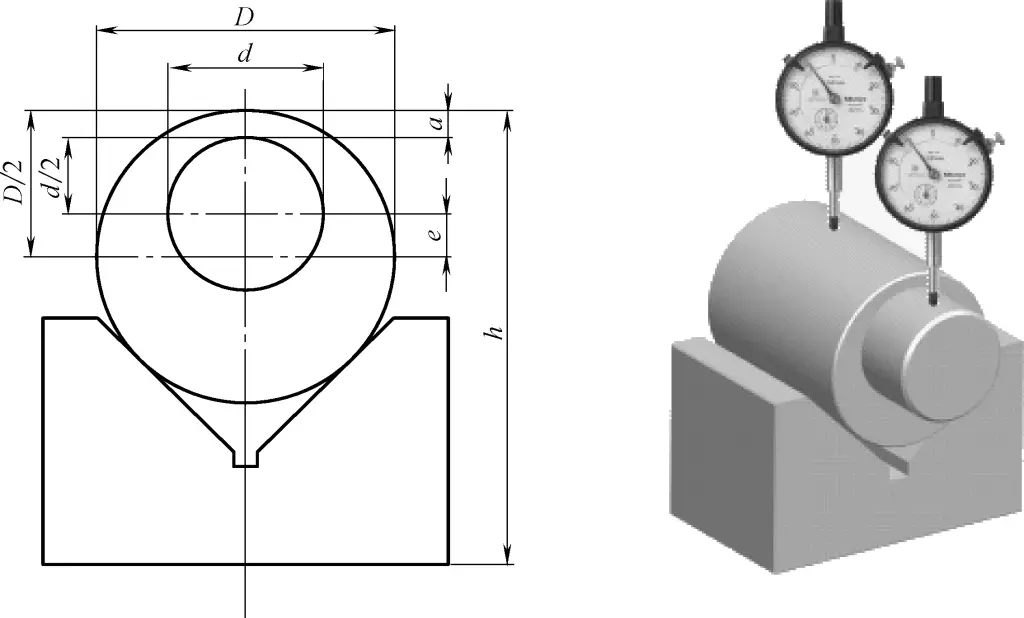
Die Werte D und d müssen mit einer Bügelmessschraube gemessen werden, dann wird die Exzentrizität e mit Hilfe der Formel berechnet. Bei exzentrischen Werkstücken auf einem Spannfutter oder bei exzentrischen Wellen mit Zentrierbohrungen an beiden Enden kann der Messfühler der Messuhr in Kontakt mit dem exzentrischen Teil gebracht werden. Drehen Sie die exzentrische Welle von Hand, und die Hälfte der Differenz zwischen dem Höchst- und dem Mindestwert, die auf der Messuhr angezeigt werden, ist die Exzentrizität e.
(3) Messung der Exzentrizität mit einer Messuhr und einem Drehkreuzschlitten.
Bei Werkstücken mit größerer Exzentrizität kann die Kreuzschlittenskala an einer Drehmaschine verwendet werden, um den begrenzten Messbereich der Messuhr auszugleichen. Bringen Sie bei der Messung zunächst die Messuhr in Kontakt mit dem exzentrischen Außenkreis des Werkstücks, ermitteln Sie den höchsten Punkt und notieren Sie den Messwert und den Wert der Kreuzschlittenskala.
Drehen Sie dann das Werkstück um 180°, bewegen Sie den Kreuzschlitten nach innen, suchen Sie den tiefsten Punkt des exzentrischen Kreises, bringen Sie die Messuhr in Kontakt mit dem tiefsten Punkt des exzentrischen Kreises und stellen Sie den Kreuzschlitten so ein, dass der ursprüngliche Messuhrwert erhalten bleibt. An diesem Punkt ist der Bewegungsabstand des Kreuzschlittens, der sich aus der Kreuzschlittenuhr ergibt, das Doppelte der Exzentrizität.
4. Inspektion von Standardgewinden
(1) Messung des großen Durchmessers.
Wenn die Anforderungen an den Gewindehauptdurchmesser nicht hoch sind und das Toleranzband breit ist, können Messschieber oder Außenmikrometer für die Messung verwendet werden.
(2) Messung der Gewindesteigung.
Die Gewindesteigung kann mit einem Stahllineal gemessen werden. Bei Regelgewinden mit allgemein kleinen Steigungen ist es am besten, die Länge mehrerer Steigungen zu messen und dann die gemessene Steigungslänge durch die Anzahl der Steigungen zu teilen, um das Maß einer einzelnen Steigung zu erhalten. Bei größeren Steigungen misst man die Länge von 2 oder 4 Steigungen und berechnet dann das Steigungsmaß.
Die Steigung von Feingewinden ist kleiner, so dass sie mit einem Stahllineal schwer zu messen ist. Im Allgemeinen wird zum Messen eine Steigungslehre verwendet. Beim Messen wird die Steigungslehre parallel zur Achsrichtung in die Zahnform eingeführt. Wenn sie perfekt passt, ist dies ein Zeichen dafür, dass die Steigung des gemessenen Gewindes korrekt ist.
(3) Messung des Teilkreisdurchmessers.
1) Messung des Steigungsdurchmessers von dreieckigen Gewinden mit einem Gewindemikrometer.
Der Aufbau und die Verwendung einer Gewindemessschraube ähneln denen einer normalen Bügelmessschraube, mit dem Unterschied, dass die beiden Messkontakte ein Kegel und eine Rille sind, die die gleiche Form wie der Gewindezahn haben. Während der Messung liegen die beiden Kontakte genau auf den Flächen des Gewindezahns auf, und der Messwert der Messschraube an diesem Punkt ist der Steigungsdurchmesser des Gewindes.
Gewindemessschrauben werden mit einer Reihe von Zahnflächenprofilen und Messkontakten für verschiedene Steigungen geliefert. Bei der Messung von Steigungsdurchmessern unterschiedlicher Spezifikationen von Dreiecksgewinden müssen die entsprechenden Messkontakte ausgetauscht werden, wie in Abbildung 23 dargestellt.

2) Drahtmessverfahren.
Auswahl des Drahtdurchmessers und der Präzision: Der Drahtdurchmesser, der die Zahnseitenfläche an der Steigungslinie des gemessenen Gewindes tangiert, wird als "bester Drahtdurchmesser" bezeichnet. Vereinfachte Formeln für den besten Drahtdurchmesser sind in Tabelle 1 aufgeführt. Durch die Verwendung des besten Drahtes für die Messung wird der Einfluss des Halbwinkelfehlers des Gewindezahns eliminiert.
Tabelle 1 Vereinfachte Formeln für den besten Drahtdurchmesser
| Gemeinsame Themen | 55° Whitworth-Gewinde | Trapezförmiges Gewinde |
| 0.57735P | 0.56370P | 0.51765P |
Zu den gebräuchlichen Drahtmessmethoden gehören die Dreidrahtmethode und die Eindrahtmethode zur Messung des Gewindesteigungsdurchmessers. Bei der Dreidrahtmethode zur Messung des äußeren Gewindesteigungsdurchmessers werden drei Drähte desselben Satzes in die Gewinderillen auf beiden Seiten des gemessenen Gewindes eingelegt, wie in Abbildung 24 dargestellt. Verwenden Sie ein präzises Messgerät wie eine Bügelmessschraube, eine Hebelmessschraube, einen optischen Komparator oder eine Längenmessmaschine, um den Abstand M zwischen den Außenseiten der Drähte direkt zu messen, und berechnen Sie dann den tatsächlichen Steigungsdurchmesser des gemessenen Gewindes.
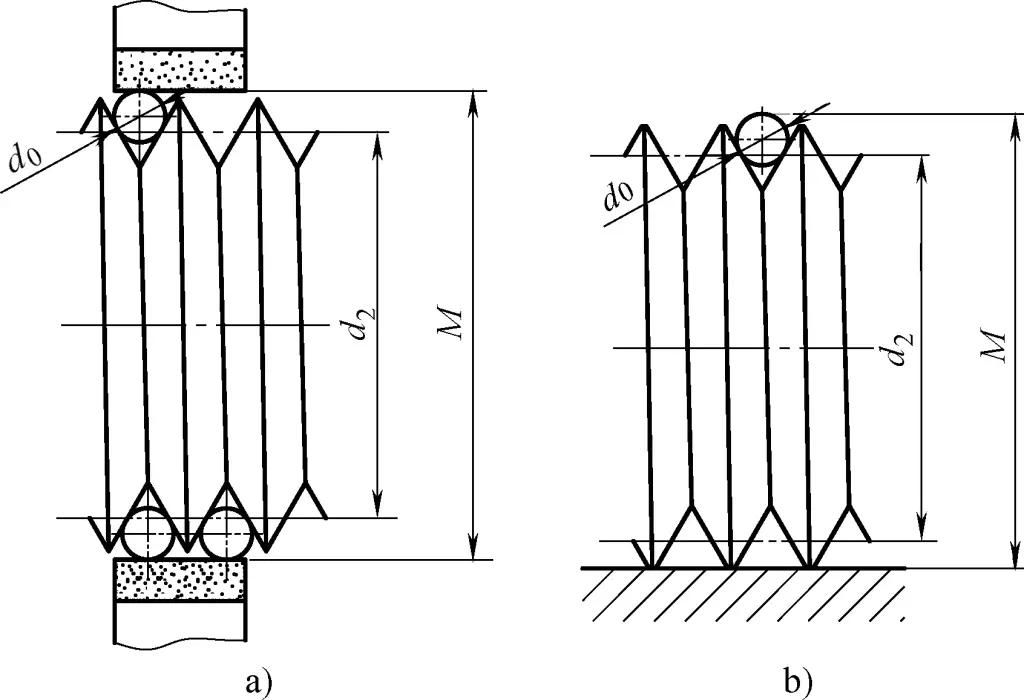
a) Drei-Draht-Messung
b) Ein-Draht-Messung
Die häufig verwendeten Drahtdurchmesserreihen sind in Tabelle 2 aufgeführt. Die Formeln zur Berechnung des Steigungsdurchmessers für gängige Gewinde sind in Tabelle 3 aufgeführt.
Tabelle 2 Häufig verwendete Drahtdurchmesserreihen
| 0.118 | 0.201 | 0.291 | 0.433 | 0.724 | 1.157 | 2.020 | 3.177 |
| 0.142 | 0.232 | 0.343 | 0.461 | 0.866 | 1.441 | 2.311 | 3.486 |
| 0.170 | 0.260 | 0.402 | 0.572 | 1.008 | 1.732 | 2.886 | - |
Tabelle 3 Berechnungsformeln für den Steigungsdurchmesser bei Regelgewinden
| Gewindetyp | Zahnwinkel α | Formel zur Berechnung des Teilungsdurchmessers |
| Gemeinsame Themen | 60° | d2 =M-(3d o -0.866P) |
| 55° Whitworth-Gewinde | 55° | d2 =M-(3,1657do -0.9605P) |
| Trapezförmiges Gewinde | 30° | d2 =M-(4,8637do -1.866P) |
(4) Umfassende Messung von Fäden.
Vor einer umfassenden Gewindemessung sollten Sie zunächst den Durchmesser, das Zahnprofil und die Steigung des Gewindes prüfen und dann Gewindelehren für die Messung verwenden. Bei der Verwendung von Gewindelehren dürfen diese nicht gewaltsam verdreht werden, um eine Beschädigung der Messfläche und eine Verringerung der Genauigkeit zu vermeiden.
Gewindelehrringe und Lehrdorne werden in der Regel für umfassende Messungen verschiedener Maßgenauigkeiten von Gewinden verwendet. Lehrringe werden für die Messung der Maßgenauigkeit von Außengewinden verwendet, während Lehrdorne für die Messung der Maßgenauigkeit von Innengewinden eingesetzt werden.
Wenn sich bei der Gewindemessung das GO-Ende des Messgeräts einschrauben lässt, das NICHT GO-Ende jedoch nicht, bedeutet dies, dass die Gewindegenauigkeit den Anforderungen entspricht. In der tatsächlichen Produktion können bei geringeren Genauigkeitsanforderungen auch Standardmuttern und -schrauben zur Prüfung verwendet werden, wobei die Leichtgängigkeit und Lockerheit beim Aufschrauben auf das Werkstück zu beurteilen ist.
5. Messung von Schneckenrädern
(1) Messung der normalen Zahndicke von Schneckenrädern mit einem Messschieber, wie in den Abbildungen 25 und 26 dargestellt.
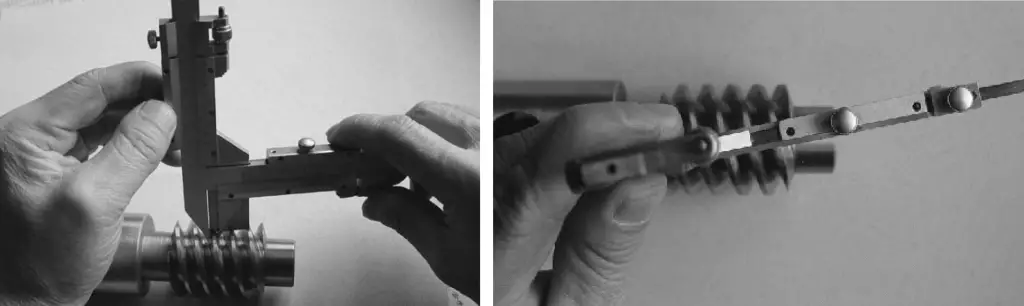
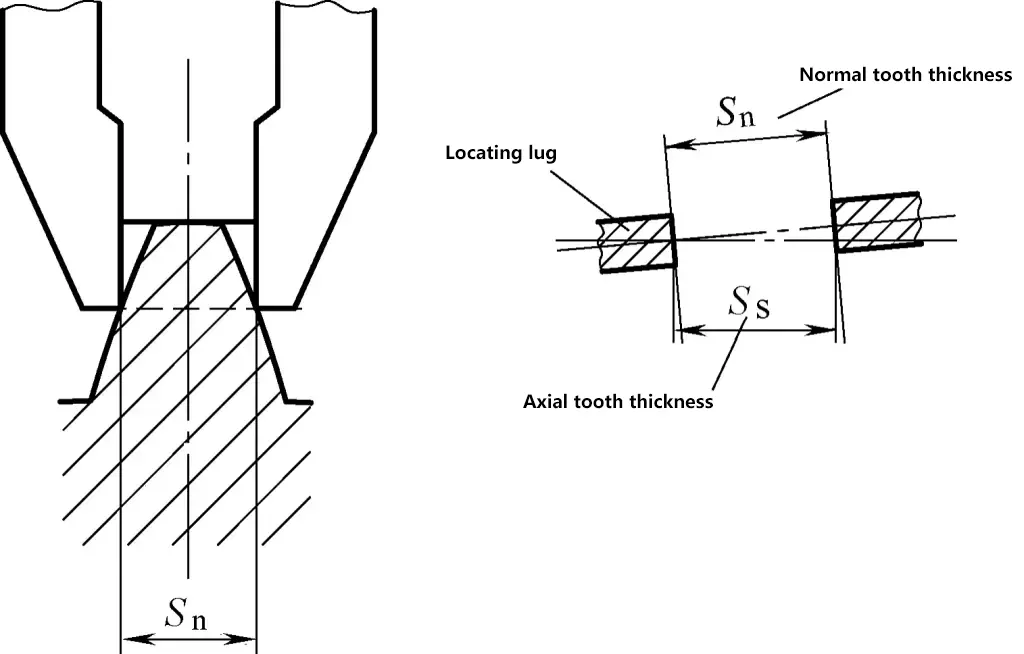
Um die Messgenauigkeit zu verbessern, kann die Zahndickenabweichung bei der Dreidrahtmessung in die Spannweitenabweichung umgerechnet und dann mit der Einzeldrahtmethode gemessen werden, wie in Abbildung 27 dargestellt. Wenn α=20° ist, lautet die Berechnungsformel für die Einzeldrahtmessung:
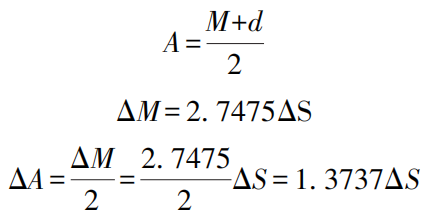
Wo
- A - Mikrometer-Messgröße bei der Eindrahtmessung (mm);
- M - Mikrometer-Messgröße bei der Dreidrahtmessung (mm);
- ΔM - Spannweitenabweichung bei der Dreileitermessung (mm);
- d - tatsächlich gemessener Außendurchmesser des Schneckenrads (mm);
- ΔA - Abweichung der Drahtmessstrecke bei der Einzeldrahtmessung (mm);
- ΔS - Zahndickenabweichung (mm).
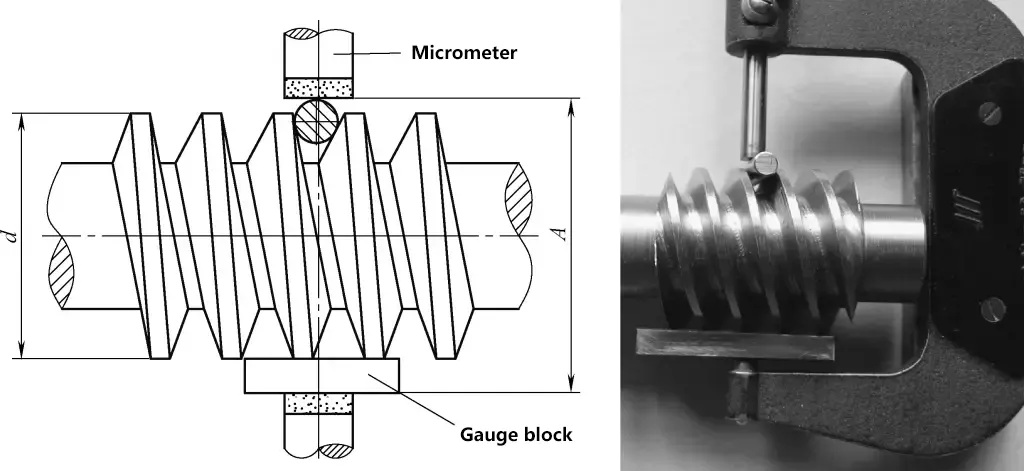
(2) Der Rundlauf des Schneckenrad-Zusatzkreises kann mit einer Messuhr auf einem Rundlaufprüfgerät überprüft werden. Drehen Sie das Schneckenrad langsam von Hand um eine volle Umdrehung. Die maximale Abweichung der Messuhranzeige ist der Rundlauffehler.
(3) Die Prüfung des Zahnprofilfehlers von Archimedes-Schneckenrädern sollte im Axialschnitt mit Hilfe von Instrumenten wie einem Universalwerkzeugmikroskop erfolgen.
Erfahrungsaustausch der Skillmaster:
Da bei der Einzeldrahtmessung der Kopfkreisdurchmesser als Messreferenz verwendet wird, obwohl d in Abbildung 27 als die tatsächlich gemessene Größe des Kopfkreises definiert ist, muss zur Gewährleistung der Messgenauigkeit die Konzentrizität zwischen dem Kopfkreisdurchmesser und dem Teilkreis des Schneckenrads während des Drehens gewährleistet sein.
III. Prüfung der allgemeinen Form- und Lagegenauigkeit
1. Erkennung von Geradheitsfehlern
(1) Erkennung von Geradheitsfehlern bei Zylindern und Quadern
Wie in Abbildung 28 dargestellt.
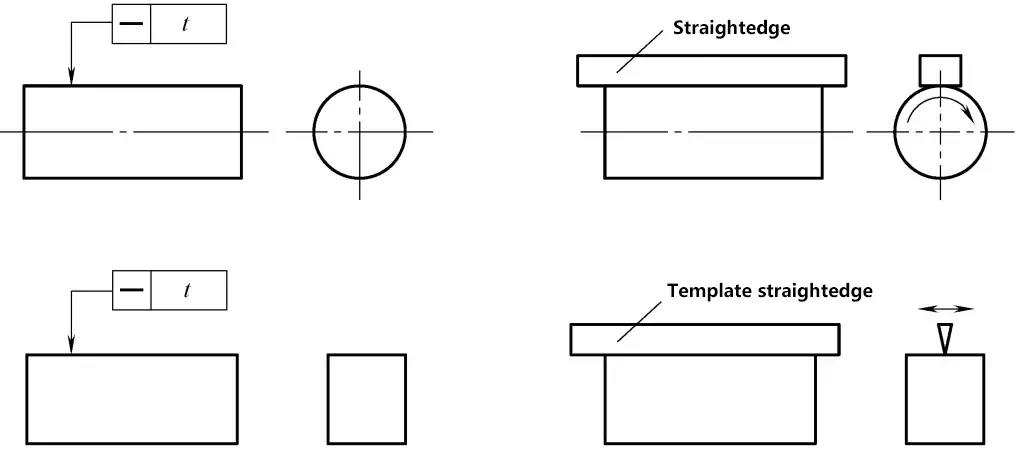
1) Inspektionswerkzeuge: Richtscheit (oder Schablonenrichtscheit), Fühlerlehre.
2) Einspann- und Arbeitsverfahren:
① Legen Sie ein Lineal oder ein Schablonenlineal direkt an die gemessene Elementlinie an und minimieren Sie den maximalen Abstand zwischen ihnen. Der maximale Abstand an diesem Punkt ist der Geradheitsfehler der gemessenen Elementlinie. Das Ausmaß des Fehlers sollte durch Messung des Lichtspalts bestimmt werden. Wenn der Lichtspalt klein ist, kann er mit einem Standard-Lichtspalt geschätzt werden; wenn er größer ist, kann eine Fühlerlehre zur Messung verwendet werden.
② Messen Sie mehrere Elementlinien nach der oben genannten Methode und nehmen Sie den größten Fehlerwert als Geradheitsfehler des gemessenen Teils.
(2) Erkennung von Geradheitsfehlern bei konischen Körpern
Wie in Abbildung 29 dargestellt.
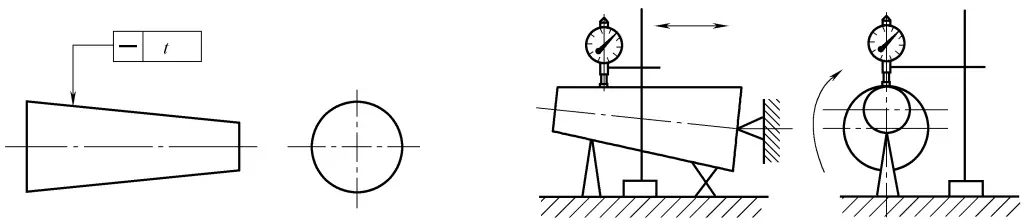
1) Prüfwerkzeuge und -ausrüstung: Planscheibe, feste und verstellbare Stützen, Messrahmen, Messuhr oder Mikrometer.
2) Montage und Arbeitsweise: Stellen Sie die beiden Endpunkte der gemessenen Elementlinie so ein, dass sie sich auf der gleichen Höhe wie die Oberflächenplatte befinden.
① Messen Sie entlang der gesamten Länge der gemessenen Elementlinie und zeichnen Sie die Messwerte auf. Berechnen Sie den Geradheitsfehler mit der Berechnungsmethode (oder der grafischen Methode) auf der Grundlage der Mindestbedingungen (oder der Zweipunktlinienmethode) unter Verwendung der aufgezeichneten Messwerte.
② Messen Sie mehrere Elementlinien nach der oben genannten Methode und nehmen Sie den größten Fehlerwert als Geradheitsfehler des gemessenen Teils.
(3) Erkennung von Geradheitsfehlern bei Wellenteilen mit einem Rundlaufprüfgerät
Wie in Abbildung 30 dargestellt.
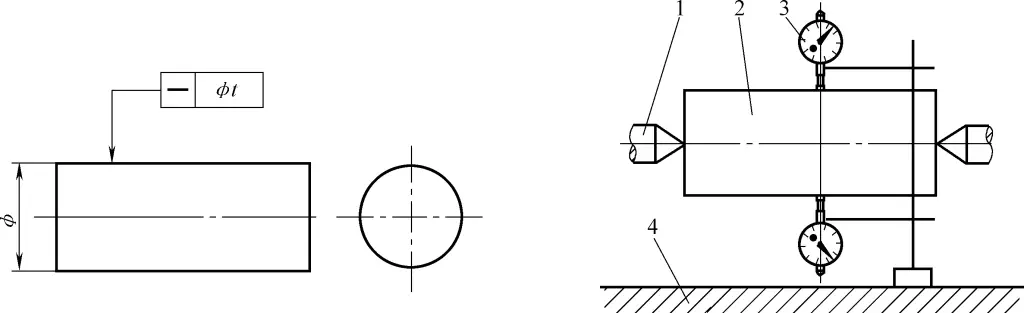
1-Center-Unterstützung
2-Gemessener Teil
3-Indikator
4-Flächenplatte
1) Prüfwerkzeuge und -geräte: Planscheibe, Zentrierhilfe oder Rundlaufprüfgerät, Messuhr, Stativ, Messuhr oder Mikrometer.
2) Montage und Arbeitsweise: Installieren Sie den gemessenen Teil zwischen zwei Zentren parallel zur Oberflächenplatte.
① Messen Sie entlang zweier Elementlinien im Querschnitt der vertikalen Achse und notieren Sie die Messwerte M₀ und M₁ der beiden Anzeiger an ihren jeweiligen Messpunkten. Nehmen Sie die Hälfte der Differenz der Ablesungen an jedem Punkt {d.h. (M₂-M₃)/2} und verwenden Sie die maximale Differenz als Geradheitsfehler der Achse in diesem Querschnitt.
② Messen Sie mehrere Elementlinien in mehreren Querschnitten mit der obigen Methode und nehmen Sie den größten Fehlerwert als Geradheitsfehler der Achse des gemessenen Teils.
2. Erkennung von Ebenheitsfehlern
(1) Messung des Ebenheitsfehlers von hochpräzisen kleinen Flugzeugen
Wie in Abbildung 31 dargestellt.
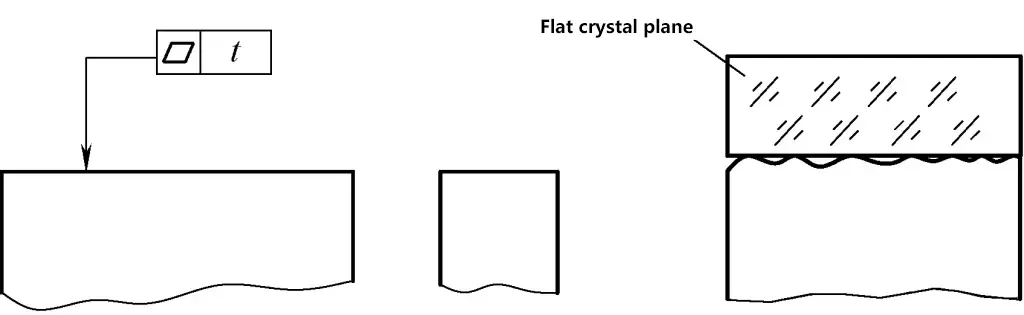
1) Inspektionswerkzeuge und -ausrüstung: Optisch flach.
2) Arbeitsweise: Legen Sie die Arbeitsfläche des optischen flach auf die gemessene Oberfläche mit leichtem Druck, und Interferenzstreifen erscheinen.
Der Ebenheitsfehler der gemessenen Oberfläche ist die Anzahl der geschlossenen Interferenzstreifen multipliziert mit der halben Wellenlänge des Lichts. Bei offenen Interferenzstreifen ist er das Verhältnis der Streifenkrümmung zum Abstand zwischen benachbarten Streifen, multipliziert mit der halben Wellenlänge des Lichts. Diese Methode eignet sich für die Messung hochpräziser kleiner Ebenen.
(2) Feststellung von Ebenheitsfehlern mit einer Wasserwaage
Wie in Abbildung 32 dargestellt.
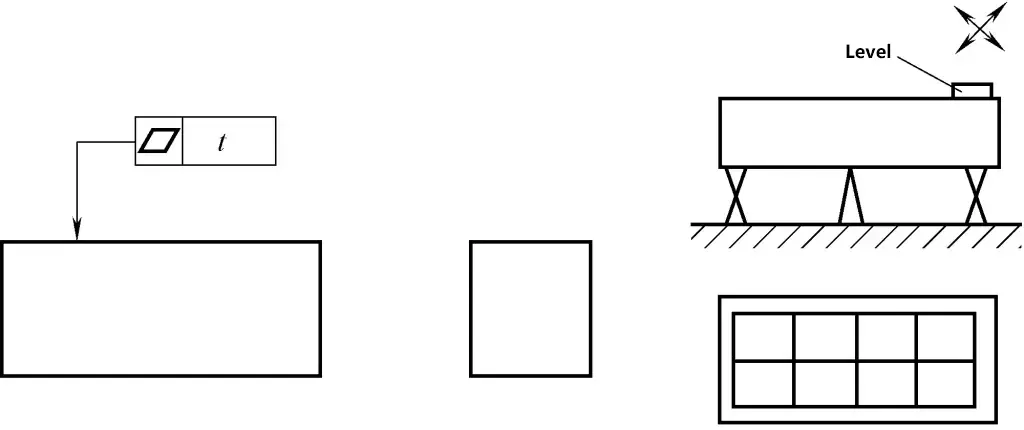
1) Inspektionswerkzeuge und -ausrüstung: Messplatte, Wasserwaage, Brückenplatte, feste und verstellbare Stützen.
2) Montage und Arbeitsweise: Stellen Sie die zu messende Oberfläche in eine horizontale Position, verwenden Sie die Wasserwaage, um die Oberfläche Punkt für Punkt nach einer bestimmten Anordnung und Richtung zu messen, zeichnen Sie die Messwerte auf und wandeln Sie sie in lineare Werte um.
Berechnen Sie den Ebenheitsfehler mit der Berechnungsmethode (oder der grafischen Methode) gemäß den Mindestbedingungen (oder der Diagonalmethode) auf der Grundlage der Werte jeder Zeile.
3. Erkennung von Rundheitsfehlern
(1) Erkennung eines der Rundheitsfehler von Kegel und Zylinder
Wie in Abbildung 33 dargestellt.
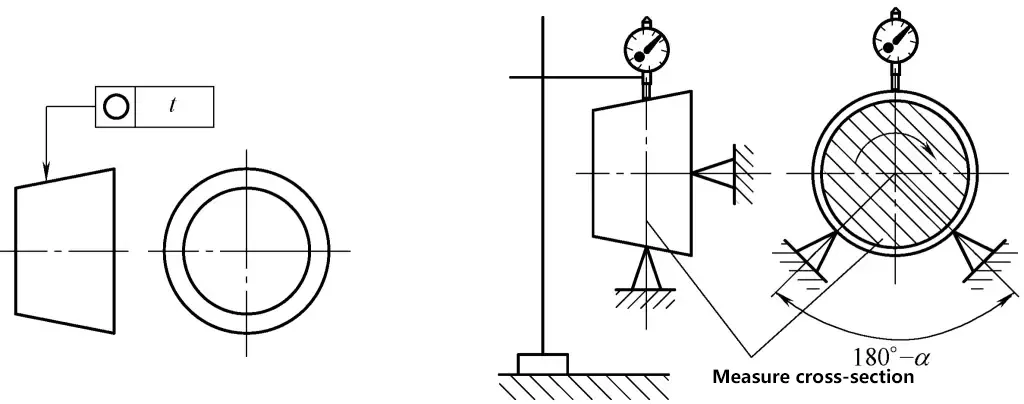
1) Inspektionsmessung und Werkzeuge: flache Platte, Messständer mit Anzeige, Prismenblock, feste und verstellbare Stützen.
2) Einspann- und Arbeitsverfahren: Legen Sie das Werkstück mit der Achse senkrecht zum Messquerschnitt auf den Prisma-Block und fixieren Sie die axiale Position.
① Während einer Umdrehung des Werkstücks entspricht die Hälfte der maximalen Differenz der Anzeigewerte dem Rundheitsfehler dieses Querschnitts.
② Messen Sie mehrere Querschnitte nach der obigen Methode und nehmen Sie den maximalen Fehlerwert als Rundheitsfehler des Werkstücks.
Die Zuverlässigkeit dieser Messmethode hängt von der kombinierten Wirkung des Querschnittsformfehlers und des Prismenwinkels ab. Üblicherweise werden die Winkel α=90° und 120° oder 72° und 108° mit zwei Prismen für getrennte Messungen verwendet.
Diese Methode eignet sich zur Messung von ungeraden Formfehlern an Innen- und Außenflächen (gerade Formfehler werden mit der Zweipunktmethode gemessen). Während der Messung kann entweder das Werkstück oder das Messgerät gedreht werden.
(2) Erkennung von Rundheitsfehlern bei Kegel und Zylinder II
Wie in Abbildung 34 dargestellt.
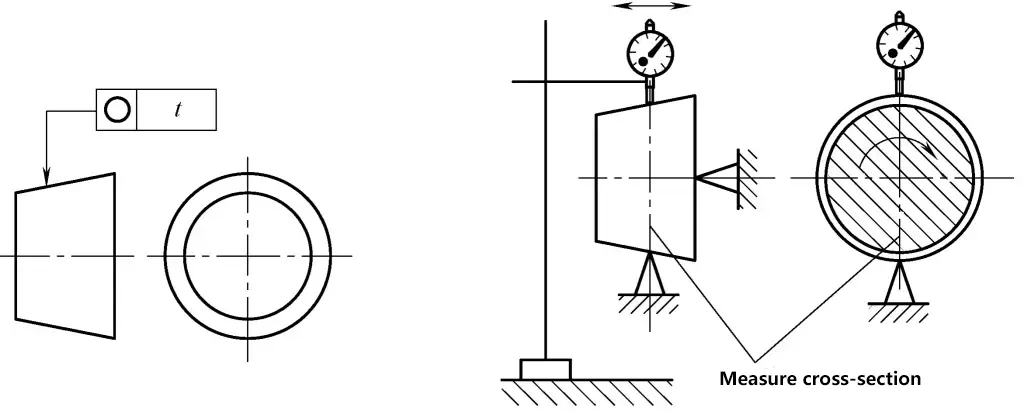
1) Inspektionsmessung und Werkzeuge: flache Platte, Messständer mit Indikator, Stütze, Mikrometer.
2) Einspann- und Arbeitsverfahren: Positionieren Sie die Werkstückachse senkrecht zum Messquerschnitt und fixieren Sie die axiale Position.
① Bei einer Umdrehung des Werkstücks ist die Hälfte der maximalen Differenz der Anzeigewerte der Rundheitsfehler eines einzelnen Querschnitts.
② Messen Sie mehrere Querschnitte nach der obigen Methode und nehmen Sie den maximalen Fehlerwert als Rundheitsfehler des Werkstücks.
Diese Methode eignet sich für die Erkennung von geradzahligen Formfehlern an Innen- und Außenflächen (ungeradzahlige Formfehler werden mit der Dreipunktmethode gemessen). Während der Messung kann entweder das Werkstück oder das Messgerät gedreht werden.
Die Zweipunktmethode zur Messung des Rundheitsfehlers ähnelt der Messung des Außendurchmessers mit einer Bügelmessschraube oder des Innendurchmessers mit einer Innenmessuhr. Messen Sie an mehreren Stellen des Umfangs und nehmen Sie die Hälfte der maximalen Differenz zwischen zwei diametral gegenüberliegenden Punkten als Rundheitsfehler.
4. Erkennung von Zylindrizitätsfehlern
(1) Erkennung des Zylindrizitätsfehlers von Zylinder und Welle I
Wie in Abbildung 35 dargestellt.
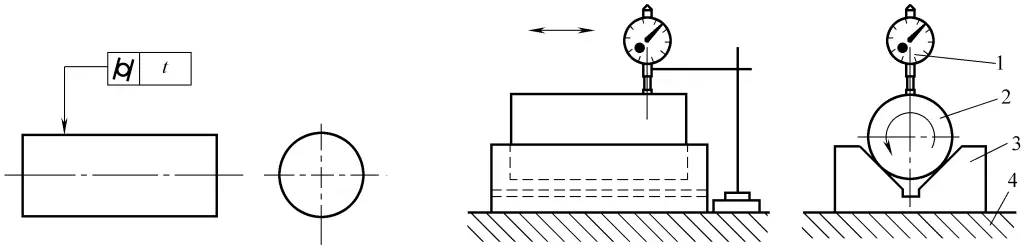
1-Indikator
2-Workpiece
3-V-Block
4-Flache Platte
1) Kontrollmessungen und Werkzeuge: flache Platte, Prismenblock, Messständer mit Anzeige.
2) Einspann- und Arbeitsmethode: Verwenden Sie die Drei-Punkt-Methode, um die Zylindrizität zu messen. Legen Sie das Werkstück in einem V-Block auf die flache Platte, wobei der V-Block länger als das Werkstück ist.
① Messen Sie während einer Umdrehung des Werkstücks den maximalen und minimalen Messwert an einem Querschnitt.
② Messen Sie mit der obigen Methode kontinuierlich mehrere Querschnitte und nehmen Sie dann die Hälfte der Differenz zwischen den maximalen und minimalen Messwerten aller gemessenen Querschnitte als den Zylindrizitätsfehler des Werkstücks. Diese Methode eignet sich für die Messung von ungeraden Formfehlern an Außenflächen.
Für eine genaue Messung werden in der Regel zwei Prismen mit Winkeln α=90° und 120° für getrennte Messungen verwendet.
(2) Erkennung des Zylindrizitätsfehlers von Zylinder und Welle II
Wie in Abbildung 36 dargestellt.
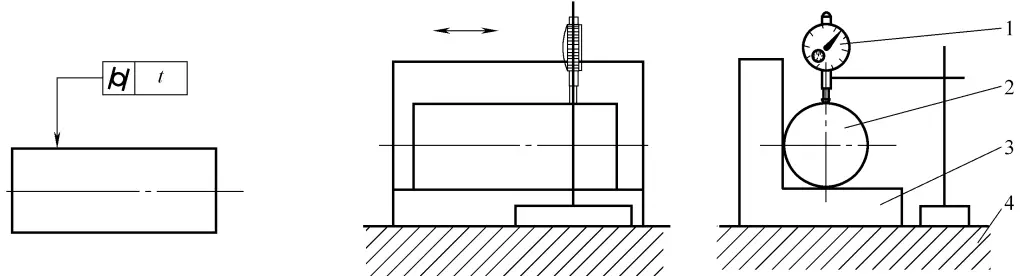
1-Indikator
2-Workpiece
3-Winkel-Sitz
4-Flache Platte
1) Kontrollmessung und Werkzeuge: flache Platte, rechtwinkliger Sitz, Messständer mit Anzeige.
2) Einspann- und Arbeitsmethode: Verwenden Sie die Zwei-Punkt-Methode, um die Zylindrizität zu messen. Legen Sie das Werkstück auf der flachen Platte, in der Nähe der rechtwinkligen Sitz.
① Messen Sie während einer Umdrehung des Werkstücks den maximalen und minimalen Messwert an einem Querschnitt.
② Messen Sie mit der obigen Methode mehrere Querschnitte und nehmen Sie dann die Hälfte der Differenz zwischen den maximalen und minimalen Messwerten aller gemessenen Querschnitte als den Zylindrizitätsfehler des Werkstücks. Diese Methode eignet sich für die Messung von gleichmäßig gelappten Formfehlern an Außenflächen.
5. Erkennung von Linienprofilfehlern
Wie in Abbildung 37 dargestellt
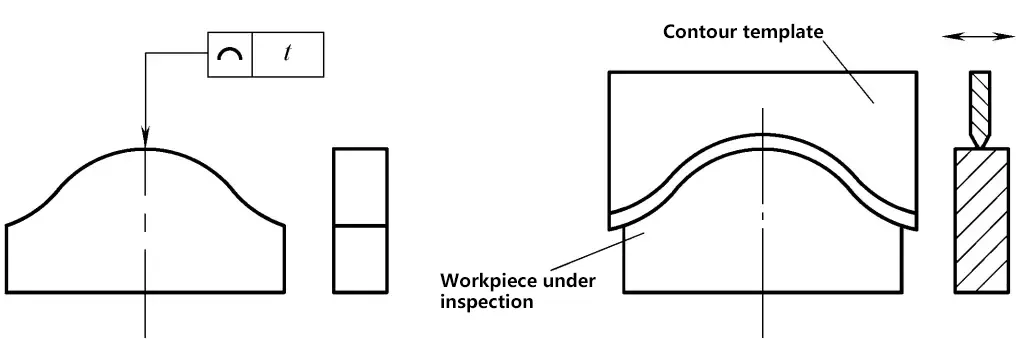
1) Inspektionsmessungen und Werkzeuge: Profilschablone.
2) Einspann- und Arbeitsmethode: Platzieren Sie die Profilschablone auf dem Werkstück in der angegebenen Richtung, schätzen Sie die Größe des Spalts mit der Lichtspaltmethode, und nehmen Sie den maximalen Spalt als den Linienprofilfehler des Werkstücks.
6. Erkennung von Parallelitätsfehlern
(1) Erkennung von Parallelitätsfehlern zwischen zwei parallelen Flächen
Wie in Abbildung 38 dargestellt.
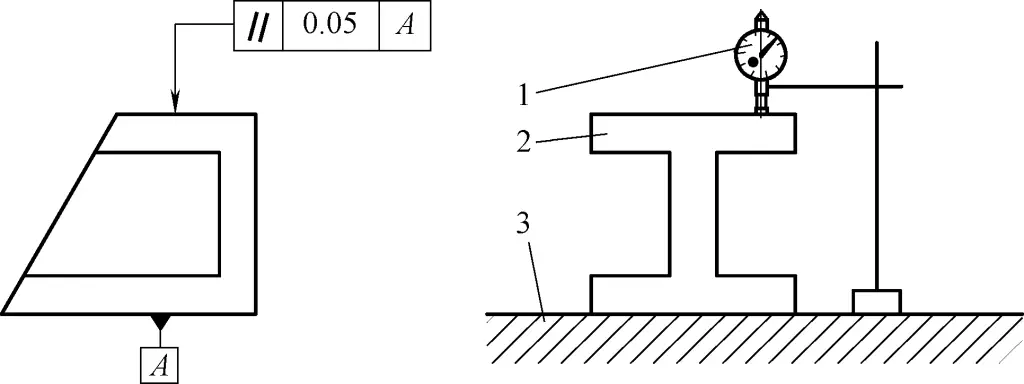
1-Indikator
2-Workpiece
3-Flache Platte
1) Kontrollmessungen und Werkzeuge: flache Platte, Stativ, Messuhr oder Mikrometer.
2) Einspann- und Arbeitsmethode: Legen Sie das Werkstück auf die flache Platte und messen Sie entlang der vorgegebenen Messlinien über die gesamte zu messende Fläche.
① Nehmen Sie die Differenz zwischen dem maximalen und dem minimalen Messwert der Anzeige als Parallelitätsfehler des Werkstücks.
② Nehmen Sie die Differenz zwischen dem maximalen und dem minimalen Anzeigewert innerhalb einer bestimmten Länge l auf jeder Messlinie als Parallelitätsfehler des Werkstücks.
(2) Erkennung des Parallelitätsfehlers der Innenbohrung relativ zur Bezugsebene
Wie in Abbildung 39 dargestellt.
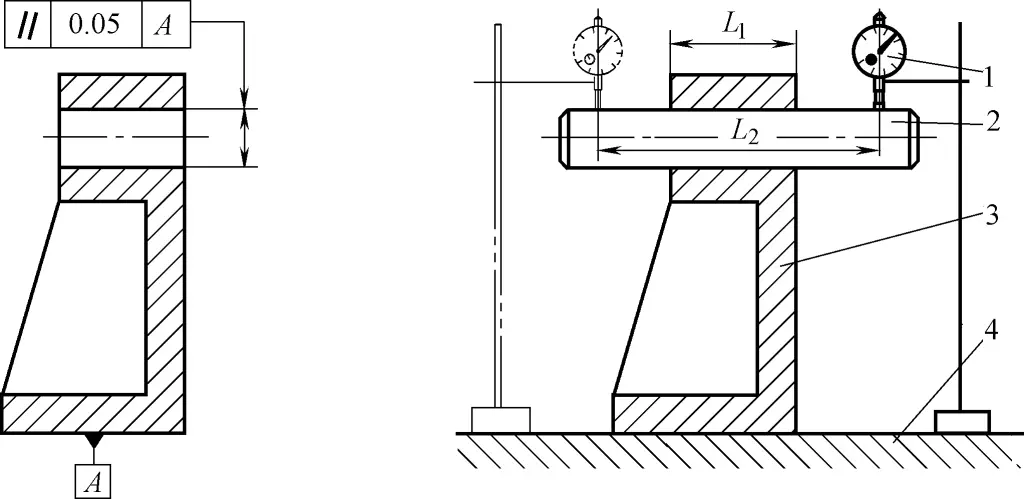
1) Kontrollmessung und Werkzeuge: flache Platte, Messständer mit Anzeige, Dorn.
2) Einspann- und Arbeitsverfahren: Legen Sie das Werkstück direkt auf die ebene Platte, wobei die zu messende Achse durch den Dorn simuliert wird. Die Messwerte M₀ und M₁ werden an zwei Positionen mit einem Messabstand von L₂ ermittelt. Dann
Parallelitätsfehler f=L₀/L₁|M₁-M₂|, wobei L₂ die Länge der Werkstückachse ist.
Verwenden Sie für die Messung einen Spreizdorn (der eine spielfreie Passung mit dem Loch bildet).
7. Erkennung von Rechtwinkligkeitsfehlern
(1) Erkennung von Rechtwinkligkeitsfehlern bei Werkstücken mit rechtwinkligem Sitz
Wie in Abbildung 40 dargestellt.
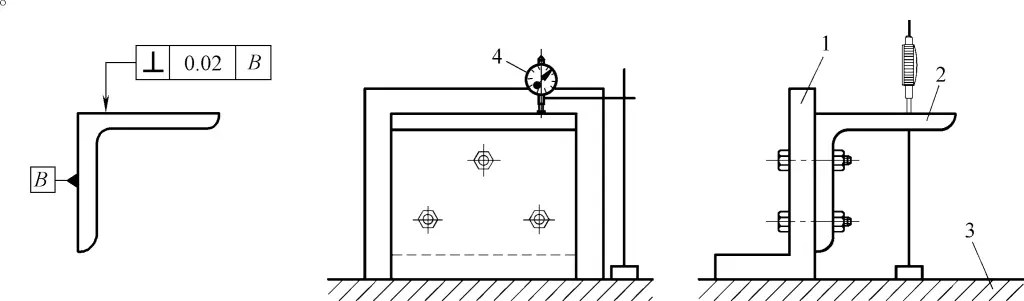
1-Winkel-Sitz
2-Workpiece
3-Flache Platte
4-Indikator
1) Kontrollmessung und Werkzeuge: flache Platte, rechtwinkliger Sitz, Messständer mit Anzeige.
2) Einspann- und Arbeitsmethode: Fixieren Sie die Referenzfläche des Werkstücks auf dem rechtwinkligen Sitz, während Sie die Messwertdifferenz der zu messenden Fläche in der Nähe der Referenz so einstellen, dass sie minimal ist. Nehmen Sie die Differenz zwischen den maximalen und minimalen Anzeigewerten, die an verschiedenen Punkten der gesamten zu messenden Oberfläche erhalten wurden, als Rechtwinkligkeitsfehler des Werkstücks.
(2) Erkennung des Rechtwinkligkeitsfehlers des Außenkreises der abgesetzten Welle relativ zur Stirnfläche
Wie in Abbildung 41 dargestellt.
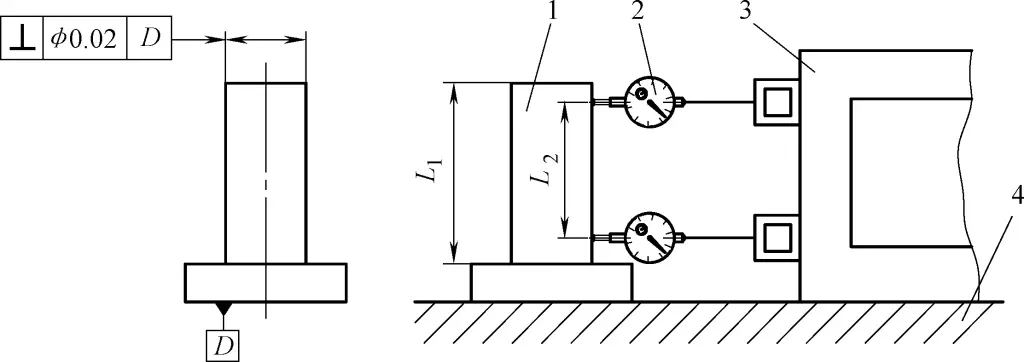
1-Arbeitsstück
2-Indikator
3-Quadrat-Box
4-Flache Platte
1) Kontrollmessungen und Werkzeuge: quadratischer Kasten, flache Platte, magnetischer Ständer mit Anzeige.
2) Einspann- und Arbeitsmethode: Legen Sie das Werkstück auf die flache Platte und messen Sie in zwei senkrechten Richtungen (x, y).
Messen Sie die Abstände M₁ und M₂ zwischen dem zu messenden Profilelement und dem quadratischen Kasten an zwei Positionen im Abstand L₀ und die entsprechenden Wellendurchmesser d₃ und d₄. Der Rechtwinkligkeitsfehler in der Messrichtung ist:
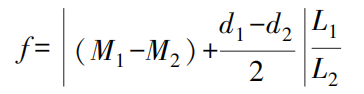
Nehmen Sie den größeren der in den beiden Messrichtungen gemessenen Fehler als Rechtwinkligkeitsfehler des Werkstücks.
8. Erkennung von Koaxialitätsfehlern
(1) Erkennung des Koaxialitätsfehlers einer abgesetzten Welle mit Mittellochreferenz
Wie in Abbildung 42 dargestellt.
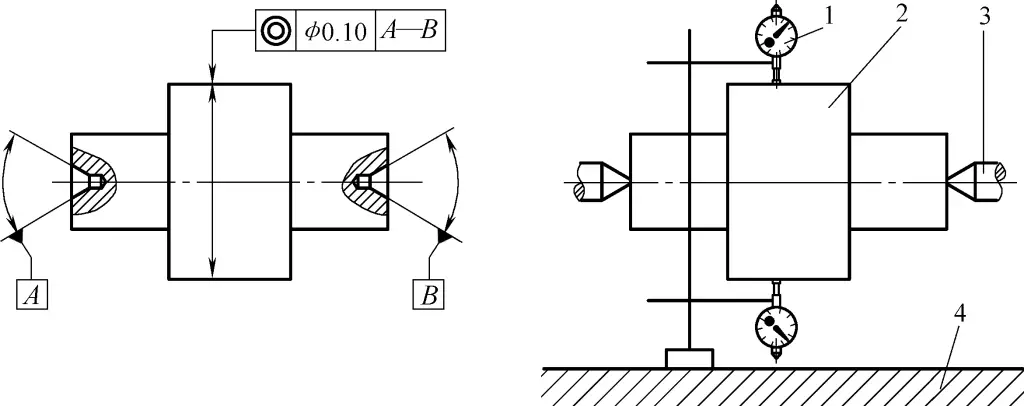
1-Indikator
2-Workpiece
3-Mitte-Stütze
4-Flache Platte
1) Inspektionsmessung und Werkzeuge: flache Platte, Mittelstütze, Messständer mit Anzeige.
2) Einspann- und Arbeitsmethode: Das Werkstück zwischen zwei Zentrierspitzen einspannen und beide Anzeiger im Querschnitt der vertikalen Achse auf Null stellen.
① Axial messen, die Differenz der Messwerte |M₀-M₁| der Anzeiger an den entsprechenden Punkten des Querschnitts senkrecht zur Bezugsachse als Koaxialitätsfehler auf diesem Querschnitt nehmen.
② Drehen Sie das Werkstück und messen Sie mehrere Querschnitte nach der oben beschriebenen Methode. Nehmen Sie den Maximalwert (Absolutwert) der aus jedem Querschnitt erhaltenen Messwertdifferenzen als Koaxialitätsfehler des Werkstücks.
(2) Erkennung des Koaxialitätsfehlers einer abgesetzten Welle ohne Mittelloch
Wie in Abbildung 43 dargestellt.
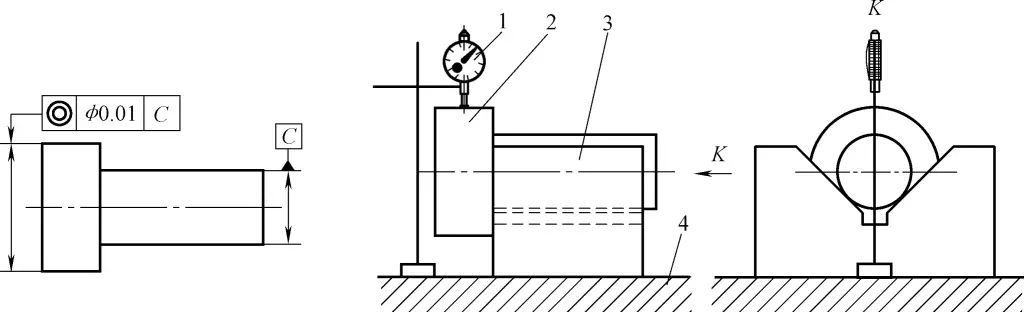
1-Indikator
2-Workpiece
3-V-Block
4-Flache Platte
1) Kontrollmessungen und Werkzeuge: flache Platte, Prismenblock, Messständer mit Anzeige.
2) Montage und Arbeitsweise: Legen Sie ein Ende der Referenzfläche des zu messenden Teils auf den V-förmigen Rahmen, dann lassen Sie den Indikator die zu messende Fläche berühren. Drehen Sie das zu messende Teil auf dem V-förmigen Rahmen für eine Umdrehung, und die Variation des Indikators ist der Koaxialitätsfehler des Teils.
(3) Feststellung des Koaxialitätsfehlers des Außenkreises im Verhältnis zum Innenloch der Hülse
Wie in Abbildung 44 dargestellt.
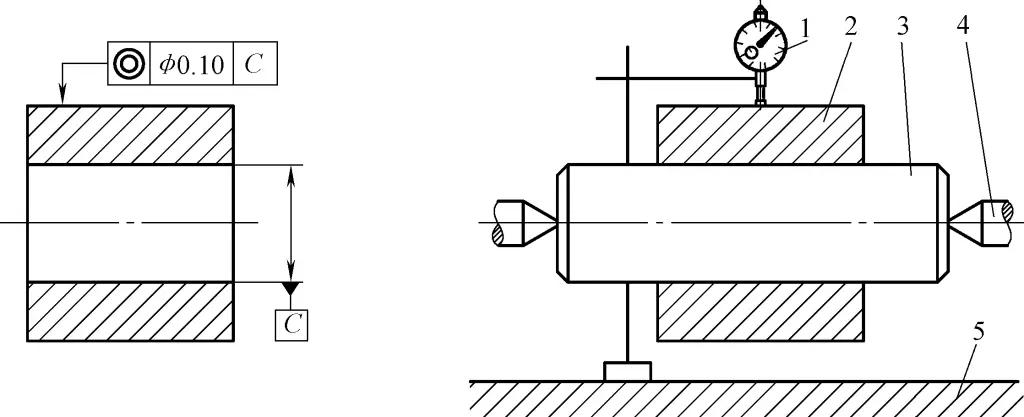
1-Indikator
2-Teil zu messen
3-Dachziegel
4-Mitte-Stütze
5-Flache Platte
1) Inspektionsmenge und Instrumente: Zentrierstütze, Dorn, Messständer mit Anzeige.
2) Montage und Arbeitsweise: Stecken Sie den Normdorn in die Bohrung des zu messenden Teils und montieren Sie ihn zwischen zwei Spitzen.
Lassen Sie den Indikator die zu messende Oberfläche berühren, drehen Sie das zu messende Teil, und die Abweichung des Indikators ist der Koaxialitätsfehler des Teils.
9. Erkennung von Symmetriefehlern
(1) Erkennung des Symmetriefehlers der Hohlkehle im Verhältnis zur Außenkontur
Wie in Abbildung 45 dargestellt.
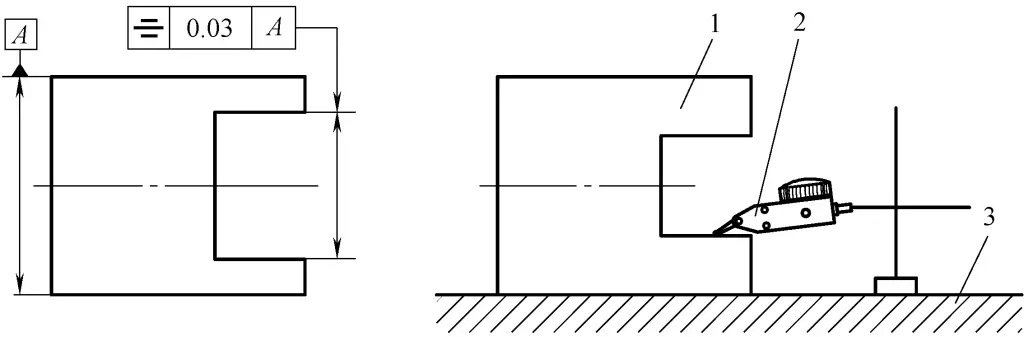
1 Zu messender Teil
2-Indikator
3-Flache Platte
1) Prüfmenge und Instrumente: Messstativ mit Hebelmessuhr, flache Platte.
2) Montage und Arbeitsweise: Legen Sie das zu messende Teil auf die flache Platte, verwenden Sie die Hebelmessuhr, um den Messwert der ersten Seite der konkaven Nut relativ zur Außenkontur (Referenz A) zu messen, setzen Sie die Messuhr auf Null, drehen Sie die Kante um, um die zweite Seite zu messen, und der absolute Wert der maximalen Messwertdifferenz ist der Symmetriefehler des zu messenden Teils.
Bei dieser Messmethode wird der Formfehler der Referenz A nicht berücksichtigt.
(2) Erkennung des Symmetriefehlers der Passfedernut auf der Welle relativ zum Wellenaußenkreis
Wie in Abbildung 46 dargestellt.
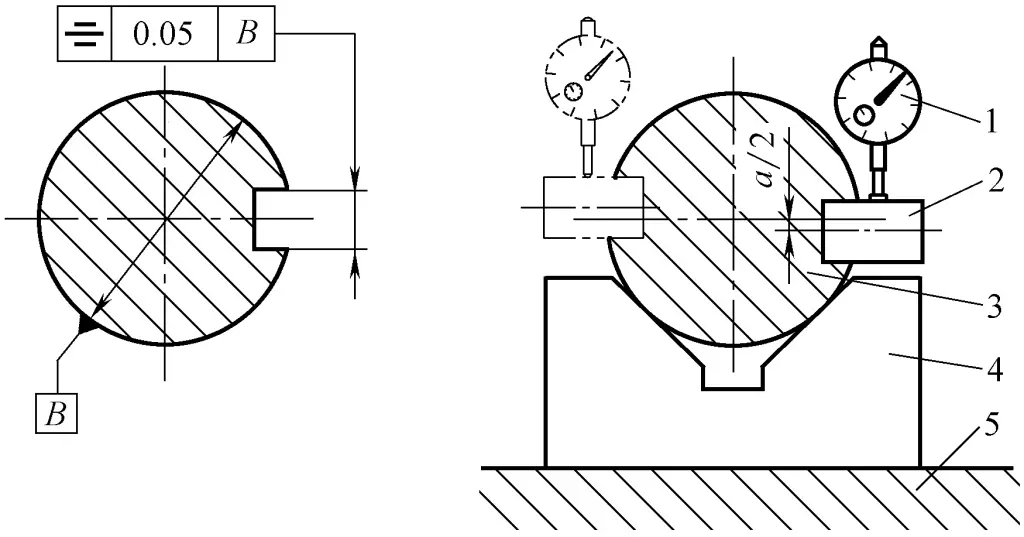
1-Indikator
2-Positionierungsblock
3 Zu messender Teil
4-V-förmiger Rahmen
5-Flache Platte
1) Inspektionsmenge und Instrumente: Flache Platte, V-förmiger Rahmen, Positionierungsblock, Messständer mit Anzeige.
2) Montage und Arbeitsweise: Die Referenzachse wird durch den V-förmigen Rahmen simuliert, und die zu messende Mittelebene wird durch den Positionierungsblock simuliert. Die Messung wird in zwei Schritten durchgeführt:
① Querschnittsmessung. Richten Sie das zu messende Teil so aus, dass der Positionierblock in radialer Richtung parallel zur ebenen Platte liegt, messen Sie den Abstand zwischen dem Positionierblock und der ebenen Platte, drehen Sie dann das zu messende Teil um 180° und wiederholen Sie die obige Messung, um die Ablesedifferenz a der beiden entsprechenden Punkte auf der oberen und unteren Seite des Querschnitts zu erhalten. Der Symmetriefehler dieses Querschnitts beträgt:
fKreuz=ah/(d-h)
Wo
- d - Durchmesser der Welle;
- h - Tiefe der Rille.
② Messung in Längsrichtung. Messen Sie entlang der Länge der Passfedernut und nehmen Sie die maximale Messwertdifferenz von zwei Punkten in Längsrichtung als Symmetriefehler in Längsrichtung:
flang=ahoch-aniedrig
Nehmen Sie den Maximalwert der in den beiden oben genannten Richtungen gemessenen Fehler als Symmetriefehler des Teils.
10. Erkennung von Rundlauffehlern
(1) Erkennung des Rundlauffehlers einer abgesetzten Welle
Wie in Abbildung 47 dargestellt.
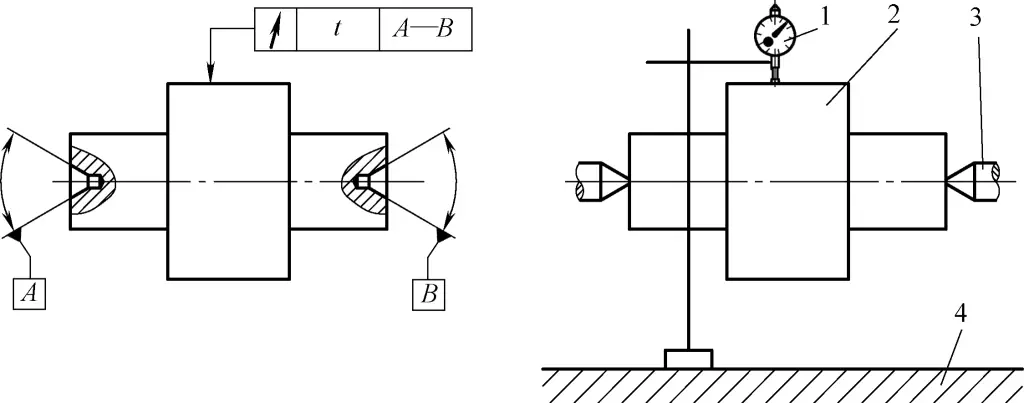
1-Indikator
2-Teil zu messen
3-Mitte-Stütze
4-Flache Platte
1) Inspektion Menge, Instrumente und Montage: Ein Paar koaxialer Zentren, Messständer mit Anzeige.
2) Montage und Arbeitsweise: Installieren Sie das zu messende Teil zwischen zwei Zentren.
① Während einer Umdrehung des zu messenden Teils ist die maximale Differenz der Anzeigewerte der radiale Rundlauffehler auf einer einzigen Messfläche.
② Messen Sie mehrere Querschnitte nach der obigen Methode und nehmen Sie den Maximalwert der an jedem Querschnitt gemessenen Rundlaufabweichung als den radialen Rundlauffehler des Teils.
(2) Ermittlung des Rundlauffehlers des Hülsenaußenkreises relativ zur Innenbohrung
Wie in Abbildung 48 dargestellt.
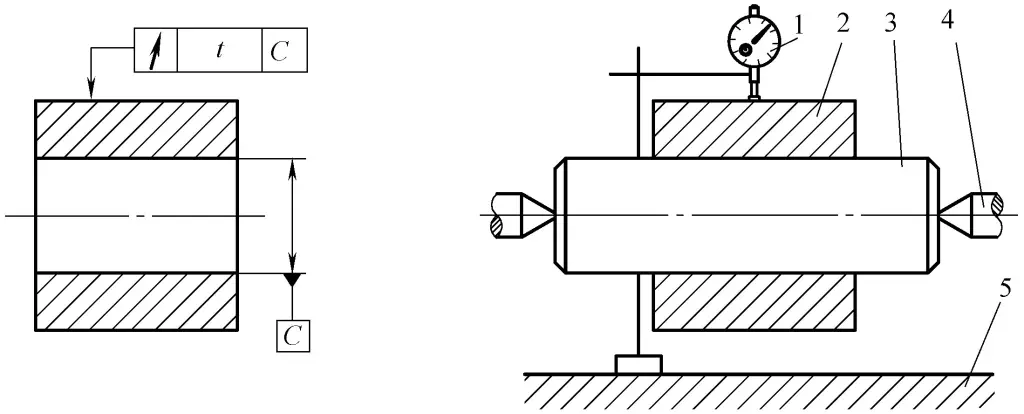
1-Indikator
2-Teil zu messen
3-Dachziegel
4-Mitte-Stütze
5-Flache Platte
1) Inspektionsmenge, Instrumente und Montage: Ein Paar koaxialer Zentrierspitzen, geführter Spreizdorn, Messständer mit Anzeige.
2) Montage und Arbeitsweise: Befestigen Sie das zu messende Teil auf dem geführten Spreizdorn und installieren Sie es zwischen zwei Spitzen.
① Während einer Umdrehung des zu messenden Teils ist die maximale Differenz der Anzeigewerte der radiale Rundlauffehler auf einer einzigen Messfläche.
② Messen Sie mehrere Querschnitte nach der obigen Methode und nehmen Sie den Maximalwert der an jedem Querschnitt gemessenen Rundlaufabweichung als den radialen Rundlauffehler des Teils.

