Para el plegado de piezas de chapa metálica, calcular el tamaño de la pieza en bruto es un requisito previo para formular el plan del proceso de plegado. Diferentes técnicos pueden seleccionar diferentes factores de tolerancia de plegado en sus documentos de proceso, y la precisión del tamaño de la pieza en bruto influye directamente en la precisión dimensional y la calidad del producto de las piezas de plegado.
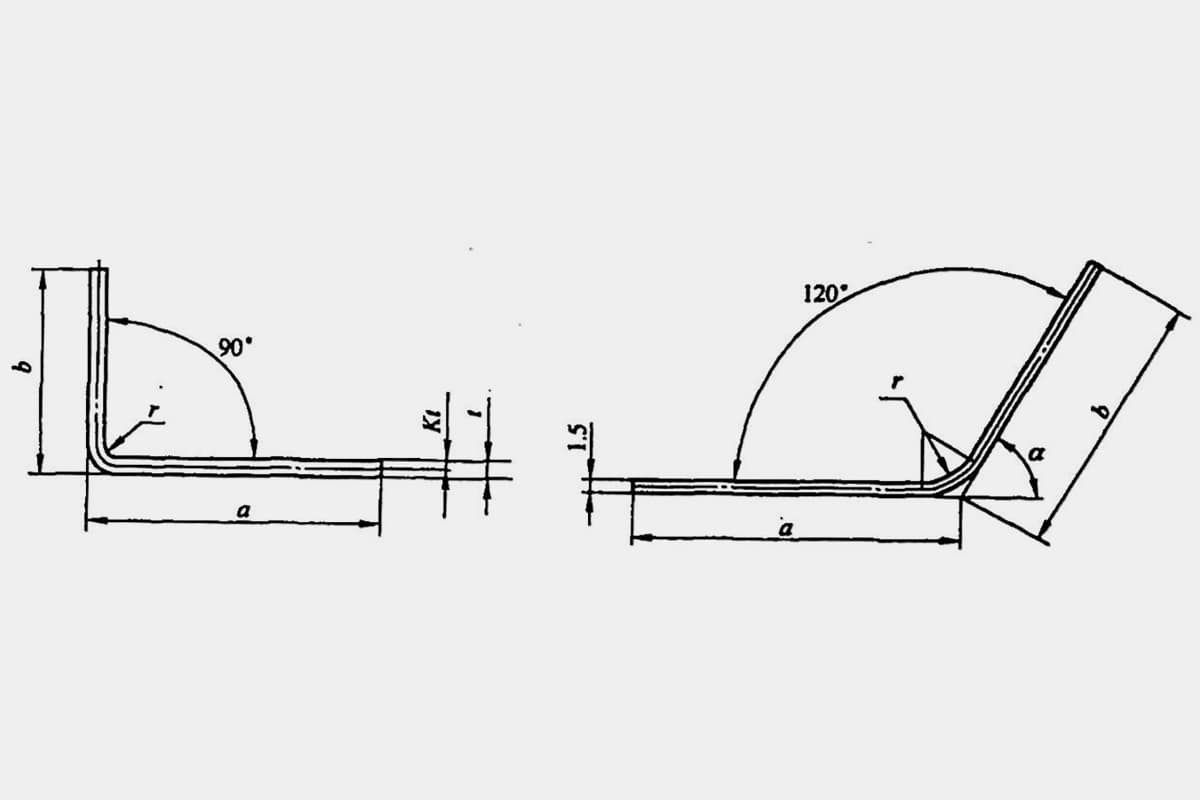
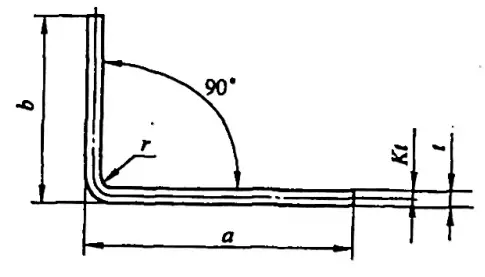
A veces, los cálculos inexactos pueden incluso dar lugar a productos de desecho. La longitud desplegada L de una pieza típica de flexión simple (véase la figura 5-1) es L = a + b - y (donde y es la deducción por flexión, también conocida como valor de corrección de la pieza R).
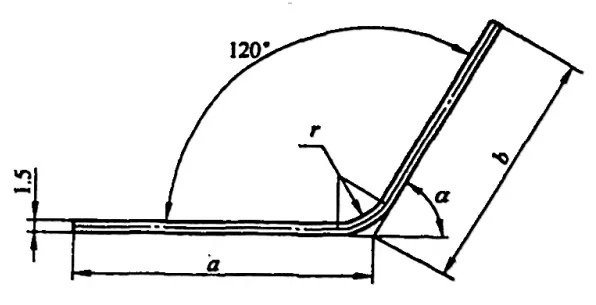
Sin embargo, en diversos manuales y materiales, la deducción por flexión para φ=90° puede obtenerse directamente, mientras que para curvas de no 90°, como las mostradas en la figura 5-2, los técnicos necesitan calcularla basándose en un factor de experiencia (factor K).
Lectura relacionada: Explicación del arte de desplegar chapas metálicas
1. Principio de cálculo de la dimensión sin plegar de las curvas de chapa metálica
La dimensión desplegada de una chapa doblada se determina basándose en el principio de que la longitud de la capa neutra permanece invariable antes y después del doblado. Cuando se dobla la chapa, las fibras de la capa exterior de la sección en blanco se estiran, y las fibras de la capa interior se comprimen.
El estiramiento de las fibras de la capa exterior disminuye gradualmente desde el exterior hacia el interior, y la compresión de las fibras de la capa interior también disminuye gradualmente desde el interior hacia el exterior.
Cuando las fibras pasan del estiramiento a la compresión o de la compresión al estiramiento, debe existir una capa de fibras en la que la tensión y la deformación sean nulas, y su longitud permanezca invariable antes y después de la flexión.
Esta capa es la que definimos como capa neutra. Por lo tanto, la clave para calcular la dimensión desplegada de la pieza en bruto doblada es determinar la posición de la capa neutra. La posición de la capa neutra se determina a partir de la condición de que el volumen de la pieza doblada y de la pieza en bruto sean iguales antes y después de la deformación plástica.
2. Determinación del radio de curvatura ρ de la capa neutra
En teoría, debido a la deformación desigual a lo largo de la dirección del grosor de la parte doblada, la capa neutra es una superficie parabólica, pero por motivos de cálculo, se suele considerar como una superficie de arco circular. Cuando la deformación por flexión es muy pequeña (r/t >6,5), se puede considerar que la capa neutra se encuentra aproximadamente en el centro del espesor del material, es decir, el radio de curvatura de la capa neutra es ρ=r+t/2.
Cuando la deformación es muy grande (r/t≤6,5), el espesor del material se hará más fino, y la distorsión de la sección es muy grande, como se muestra en la Figura 5-3.
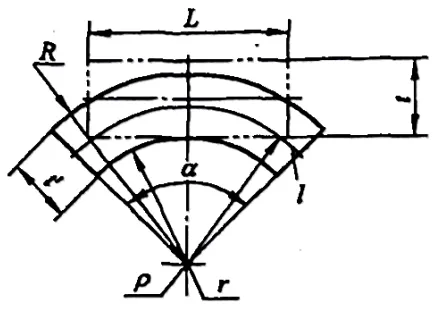
En este momento, para satisfacer la condición de equilibrio según la cual la fuerza resultante de todas las fuerzas actuantes en la sección es nula, la capa neutra debe desplazarse hacia la superficie interior del material.
En este punto, podemos determinar el radio de curvatura de la capa neutra basándonos en la condición de que el volumen no cambia durante la deformación plástica, es decir, el volumen antes de la flexión: V0=LBt, y el volumen después de la flexión:
V=(R2-r2)α*B'/2.
En la fórmula, B es la anchura de la pieza en bruto (mm); B' es la anchura media de la pieza en bruto después del curvado (mm); α es el ángulo central de curvado. Según el principio de que el volumen es igual antes y después del curvado, tenemos V0=V, eso es,
LBt=(R2-r2)α*B'/2, y L=(R2-r2)α*B'/2tB (5-1).
A partir de la tensión y deformación nulas de la capa neutra, obtenemos L=l=αρ, donde L es la longitud antes de la deformación de la capa neutra (mm), y l es la longitud después de la deformación de la capa neutra (mm).
Sustituyendo la ecuación (5-1), obtenemos ρ=(R2-r2)B'/2tB. Si sustituimos R=r+t' en la ecuación anterior, podemos obtener otra forma de la ecuación ρ=(r/t+η/2)tβη (5-2), donde β es el factor de anchura, β=B'/B, y generalmente cuando se dobla una placa ancha (B>3t), se suele considerar que β=1; η es el factor de adelgazamiento, η=t'/t.
La ecuación (5-2) es la fórmula para calcular teóricamente la posición de la capa neutra. Para calcularla, debemos conocer η, es decir, la regla de adelgazamiento. El valor de η puede consultarse en la Tabla 5-1.
Hay que señalar que la regla de adelgazamiento es bastante compleja, la distribución de la posición de la capa neutra en la zona de doblado no es uniforme, y la regla de adelgazamiento también está relacionada con muchos factores, como el método de doblado, la anchura de la ranura de la matriz inferior de doblado y el grosor del material.
Esto aporta errores inevitables al cálculo teórico de la posición de la capa neutra, reduciendo así el valor de aplicación práctica del método de determinación teórica.
Cuadro 5-1: Factor de adelgazamiento η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
En la producción real, se suele utilizar una fórmula empírica, más sencilla que el cálculo teórico, para determinar la posición del eje neutro, como se indica a continuación:
ρ = r + Kt (5-3)
Dónde:
- ρ - Radio de curvatura del eje neutro (mm)
- r - Radio interior de curvatura de la materia prima (mm)
- t - Espesor del material (mm)
- K - Coeficiente del eje neutro (empírico) Factor K), consulte la Tabla 5-2
Cuadro 5-2: Valores empíricos del coeficiente del eje neutro K
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
Nota:
- K1 es aplicable a curvas en forma de V o de U con una placa superior o una placa de prensado.
- K2 es adecuado para curvas en V sin placa superior.
3. Cálculo de las dimensiones en blanco sin plegar de varias curvas típicas de chapa metálica
Basándose en la definición de la capa neutra, la dimensión desplegada de la pieza en blanco debe ser igual a la longitud de la capa neutra. Normalmente, basándose en la radio de curvatura r de la pieza en bruto, las curvas se clasifican en curvas con esquinas redondeadas y curvas sin esquinas redondeadas: las curvas se consideran con esquinas redondeadas cuando r>0,5t, y sin esquinas redondeadas cuando r<0,5t.
Además, en función de la anchura de la chapa B, las curvas se clasifican en curvas de chapa ancha y estrecha: cuando la anchura de la chapa B>3t, se denomina curva de chapa ancha, y cuando la anchura de la chapa B<3t, se denomina curva de chapa estrecha.
En la práctica de producción, las curvas con radio de esquina redonda (r>0,5t) y chapas anchas (B>3t) son las más utilizadas, y teniendo en cuenta la universalidad de las curvas, discutimos principalmente el cálculo de las dimensiones desplegadas de la chapa para curvas con radio de esquina redonda y chapas anchas durante el curvado.
3.1 Cálculo de las dimensiones en vacío para curvas redondas (r>0,5t)
Cuando r>0,5t, B>3t, debido a que el adelgazamiento de la parte doblada no es severo y la distorsión de la sección transversal es pequeña, la longitud de la pieza en bruto puede determinarse basándose en el principio de que la longitud de la capa neutra es igual a la dimensión desplegada de la pieza en bruto.
Los métodos habituales de cálculo de las dimensiones desplegadas en bruto de las curvas de esquina redonda (r>0,5t) se dividen en: el cálculo del coeficiente de flexión y el cálculo del valor de deducción por flexión.
1. Cálculo del coeficiente de curvatura para dimensiones en blanco sin plegar:
1) El coeficiente de flexión es la longitud de la parte de arco medida a lo largo de la capa neutra de la zona de deformación por flexión (parte R de flexión), como se muestra en la figura 5-4.
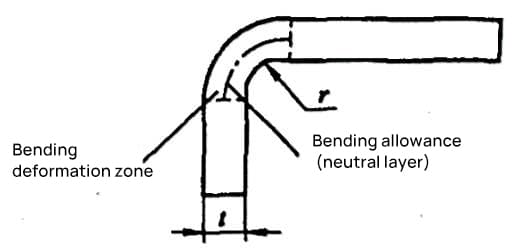
El coeficiente de flexión se calcula mediante la fórmula (5-4): x=παρ/180° (5-4)
Donde ρ es el radio de curvatura de la capa neutra (mm).
2) La figura 5-5 muestra un ejemplo de notación de dimensiones para el cálculo del coeficiente de flexión de las dimensiones de la pieza en bruto desplegada, y su fórmula para calcular el coeficiente de flexión de las dimensiones de la pieza en bruto desplegada es la siguiente.

a) φ > 90° b) φ≤90
L=a+b+x (5-5)
Sustituyendo la ecuación (5-3) en la ecuación (5-4), obtenemos la fórmula del coeficiente de flexión:
x=πα(r+Kt)/180° (5-6)
Sustituyendo la ecuación (5-6) en la ecuación (5-5), obtenemos la fórmula para calcular el tamaño desplegado de la pieza en bruto doblada:
L=a+b+πα(r+Kt)/180° (5-7)
Dónde:
- L - Tamaño desplegado de la pieza en bruto (mm);
- K - Coeficiente del factor K, consulte su valor en la Tabla 5-2;
- α - El ángulo central de flexión, su relación con el ángulo de la parte doblada es α=180°-φ;
- r - El radio de curvatura de la capa interior de la pieza en bruto (mm);
- t - Espesor del material (mm);
- a, b - Las longitudes de las partes rectas del componente (mm), respectivamente.
2. Cálculo de la deducción por flexión para el tamaño desplegado de una pieza doblada de esquina redondeada (r>0,5t)
1) La deducción por flexión (también conocida como valor de corrección de la parte R) es la diferencia entre el doble de la R de la zona de deformación por flexión (la parte R de la curva) y el coeficiente de flexión, como se muestra en la figura 5-6.

La deducción por flexión (valor de corrección de la parte R) se calcula según la ecuación (5-8):
y = 2R-παr/180° (5-8)
2) La figura 5-7 muestra un ejemplo de anotación de dimensiones para el cálculo de la deducción por flexión para el tamaño desplegado de la pieza en bruto. La deducción por flexión y se calcula mediante la siguiente fórmula:
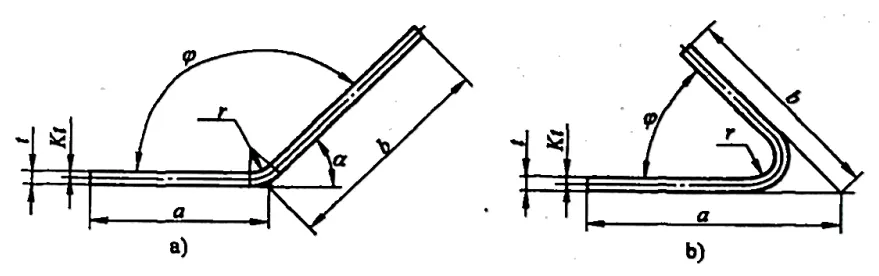
a)90°<φ≤165° b)φ≤90°
①Cuando φ ≤ 90°:
R=(r+t)/tan(φ/2)
Sustituyendo la fórmula anterior y la fórmula (5-3) en la fórmula (5-8), obtenemos la deducción de flexión (es decir, el valor de corrección de la parte R) para una flexión φ≤90° (véase la figura 5-7b):
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
②Cuando 90°<φ≤165°:
R=(r+t)tan[(180°-φ)/2]
Sustituyendo la fórmula anterior y la fórmula (5-3) en la fórmula (5-8), obtenemos la deducción por flexión (es decir, el valor de corrección de la parte R) para una flexión 90°<φ≤165° (véase la figura 5-7a):
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
③Cuando 165°<φ≤180°:
y≈0
3) La fórmula para calcular el valor de la deducción por flexión del tamaño de la pieza en bruto de la pieza mostrada en la Figura 5-7 es:
L=a+b-y (5-11)
①Cuando φ≤90°, sustituyendo la fórmula (5-9) en la fórmula (5-11), obtenemos la fórmula para calcular el valor de deducción por flexión del tamaño de la pieza en bruto como sigue:
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
②Cuando 90°<φ≤165°, sustituyendo la fórmula (5-10) en la fórmula (5-11), obtenemos la fórmula para calcular el valor de deducción por flexión del tamaño de la pieza en bruto como sigue:
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
③Cuando 165°<φ≤180°:
L≈a+b (5-14)
Dónde,
- y - Deducción por flexión (mm)
- L - Tamaño en blanco de la pieza (mm)
- r - Radio de curvatura interior de la pieza bruta (mm)
- t - Espesor del material (mm)
- α - Ángulo del centro de doblado, su relación con el ángulo de doblado es α=180°-φ
- a, b-Longitudes de los bordes de la pieza (mm) hasta el vértice de flexión.
3. Cálculo del tamaño de la pieza en bruto para curvas multiángulo
Para las curvas multiángulo, el tamaño de la pieza en bruto es la suma de la parte R y las longitudes de las aristas rectas.
1) Cálculo del tamaño de la pieza en bruto de curvatura multiángulo mediante el coeficiente de curvatura:
L=l1+l2+...+ln+1+nx (5-15)
Donde l1, l2...ln+1 son las longitudes de las partes rectas de cada arista de la pieza (mm);
n es el número de curvas R.
2) Cálculo del tamaño de la pieza en bruto de plegado multiángulo mediante la deducción de plegado:
L=l1+l2+...+ln+1-ny (5-16)
Donde l1, l2...ln+1 son las longitudes de los bordes de la pieza (mm) hasta el vértice de flexión;
n es el número de curvas R.
Ejemplo 5-1: Calcular el tamaño de la pieza en bruto para la curva mostrada en la Figura 5-8.
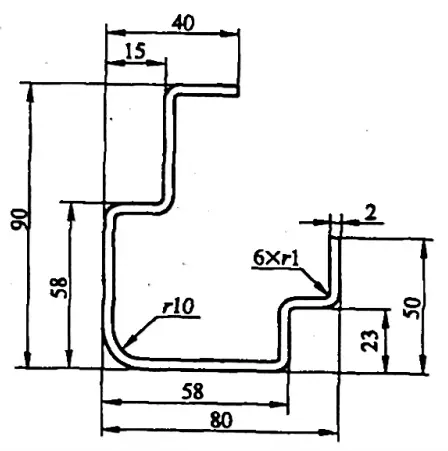
Solución 1: Calcule el tamaño de la pieza en bruto utilizando el coeficiente de flexión.
Consulte el Apéndice A: Cuando el ángulo de la pieza de flexión φ=90°, el espesor t=2mm y el radio r=10mm, el coeficiente de flexión es de 2,68mm;
Cuando el ángulo de la pieza de flexión es de 90°, el espesor t=2mm y el radio r=10mm, el coeficiente de flexión es x2=16,9mm.
A partir de las ecuaciones (5-5) y (5-15), el tamaño plano de la pieza en bruto para la pieza doblada se calcula como:
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2,68 + 16,9]mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240,98 mm.
Solución 2: Calcule el tamaño plano de la pieza en bruto utilizando el valor de la deducción por flexión.
Consulte el Apéndice C: Para una curva con un ángulo φ=90°, espesor t=2mm, y radio r=1mm, el valor de corrección para la sección R es y1=3,32mm; para una curva con un ángulo φ=90°, espesor t=2mm, y radio r=10mm, el valor de corrección para la sección R es y2=7,1mm.
El tamaño bruto de la parte doblada puede obtenerse a partir de las ecuaciones (5-11) y (5-16):
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3,32 - 7,1] mm
= (25+34+17+116+25+24+27-19,92-7,1) mm
= 240,98 mm
Ejemplo 5-2: Calcular el tamaño bruto de la pieza doblada mostrada en la Figura 5-9.
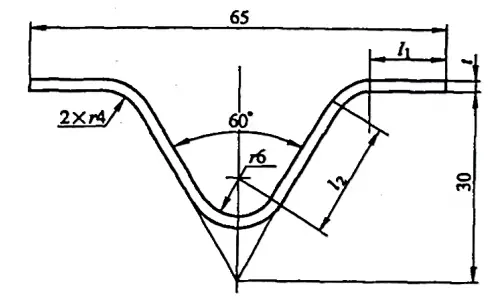
Solución: Calcular el tamaño bruto utilizando el coeficiente de flexión.
La fórmula para calcular las dimensiones en bruto de la pieza doblada a partir de las ecuaciones (5-5) y (5-15) es:
L=2l1+2l2+2x1+x2
donde l1 = [32,5 - (30tan30°+4tan30°)] mm = 12,87 mm
y l2 = [(30/cos30°) - (8/tan30°+4tan30°)] mm = 18,47 mm
Referencia al Apéndice A: cuando el ángulo de curvatura φ=120°, t=2mm, r=4mm, el valor del factor de curvatura es x1=4,98mm; cuando el ángulo de curvatura φ=60°, t=2mm, r=6mm, el valor del factor de curvatura es x2=14,16 mm.
Sustituyendo estos valores en la fórmula se obtiene la longitud de la pieza en bruto desplegada como L= (2×12,87 + 2×18,47 + 2×4,98 + 14,16) mm = 86,8 mm.
Cabe señalar que, en el caso de curvas más sencillas con menores requisitos de precisión, las dimensiones de la pieza en bruto desplegada pueden calcularse directamente. Sin embargo, para curvas más complejas o con mayores requisitos de precisión, la forma y las dimensiones de la pieza en bruto desplegada deben probarse repetidamente y revisarse continuamente para confirmar la forma y las dimensiones de la pieza en bruto.
3.2 Cálculo de las dimensiones de desarrollo de la pieza en bruto para componentes de curvatura pronunciada (r<0,5t)
Cuando el radio de curvatura r de un componente es inferior a 0,5t, se habla de curvatura cerrada. El cálculo de la dimensión de desarrollo de la pieza en bruto para este tipo de componentes se basa en el principio de la consistencia del volumen antes y después del doblado.
En las curvas cerradas, debido al fuerte adelgazamiento del material en la curva, el proceso de deformación es extremadamente complejo, lo que dificulta el cálculo exacto de las dimensiones de desarrollo de la chapa. Por lo tanto, las dimensiones de desarrollo de la chapa calculadas deben corregirse basándose en datos empíricos o mediante doblado de prueba.
La fórmula de cálculo de las dimensiones de desarrollo en bruto de los componentes de curvatura pronunciada (r<0,5t, φ=90°) se encuentra en la Tabla 5-3.
Tabla 5-3 Fórmula de cálculo de las dimensiones de desarrollo en bruto de los componentes de curvatura cerrada (r<0,5t, φ=90°) (unidad: mm)
| Número de serie | Características de flexión | Esquema | Fórmula |
| 1 | Dobla una esquina. |  | L=a+b+0,4t |
| 2 | Aplástalo. |  | L=a+b-0,43t |
| 3 | Dobla dos esquinas a la vez. | 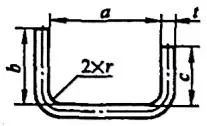 | L=a+b+c+0,6t |
| 4 | Dobla tres esquinas simultáneamente. | 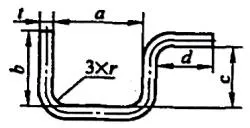 | L=a+b+c+d+0,75t |
| 5 | Doblar dos esquinas en el primer caso, y doblar otra esquina en el segundo. | L=a+b+c+d+t | |
| 6 | Doblar cuatro esquinas al mismo tiempo. | 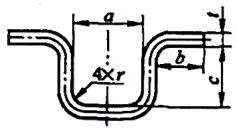 | L=a+2b+2c+1,2t |
| 7 | Doblar para formar cuatro esquinas en dos instancias. | L=a+2b+2c+1,2t |
3.3 Cálculo de las dimensiones sin plegar de las piezas plegables tipo bisagra
Para bisagra piezas curvadas con r= (0,6~3,5)t (consulte la Figura 5-10), el proceso de rebordeado suele seguir el patrón mostrado en la Figura 5-11. Durante el rebordeado, el espesor de la chapa aumenta y la capa neutra se desplaza hacia el exterior. Las dimensiones desplegadas de la chapa se pueden calcular de forma aproximada mediante la siguiente fórmula:
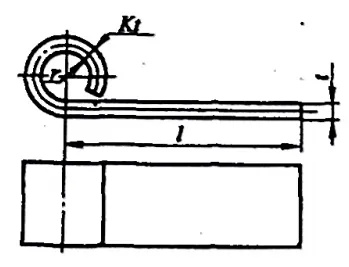
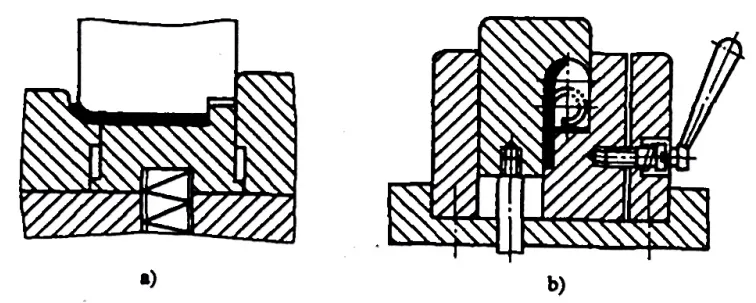
- a) Primera operación
- b) Segunda operación
L=l+1,57π(r+Kt)+r
Dónde:
- L - Dimensiones sin plegar de la pieza en bruto (mm);
- l - Longitud del segmento recto (mm);
- r - Radio de curvatura interior de la pieza bruta (mm);
- K - Coeficiente de desplazamiento de la capa neutra. Cuando r/t=0,5~1,8, K se suele tomar como 0,5~0,70 (cuanto menor sea el valor de r/t, mayor será el valor de K; a la inversa, menor será el valor de K). También puede seleccionarse según la Tabla 5-4.
Tabla 5-4 Coeficiente de desplazamiento de la capa neutra para piezas de flexión tipo bisagra
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |