La fuerza de flexión es una base importante para diseñar procesos de estampación, seleccionar prensas y diseñar moldes.
Dado que la magnitud de la fuerza de flexión está relacionada no sólo con el tamaño de la pieza en bruto, las propiedades mecánicas del material, la distancia entre los soportes de la matriz, el radio de flexión y la holgura entre los moldes, sino también en gran medida con el método de flexión, es difícil realizar cálculos precisos utilizando métodos de análisis teóricos. Por lo tanto, en la producción se suelen utilizar las fórmulas empíricas que figuran en la Tabla 1 para realizar un cálculo aproximado de la fuerza de flexión.
I. Bases y métodos de cálculo teórico de la fuerza de flexión
El método de cálculo teórico de la fuerza de flexión se deriva bajo las condiciones de equilibrio estático que la suma de varias fuerzas externas que actúan sobre la pieza en bruto de flexión es cero, y el par externo que actúa sobre la pieza en bruto de flexión es igual a su par de resistencia interna, a través del cálculo convencional.
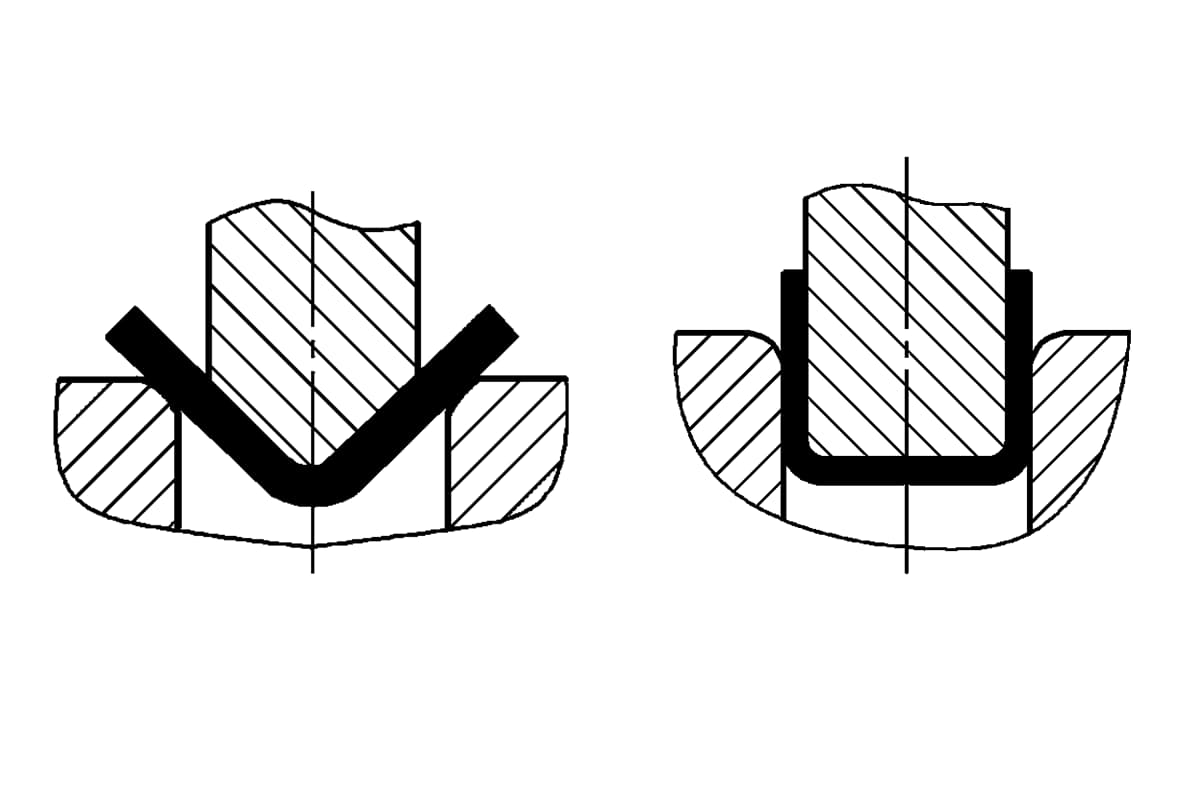
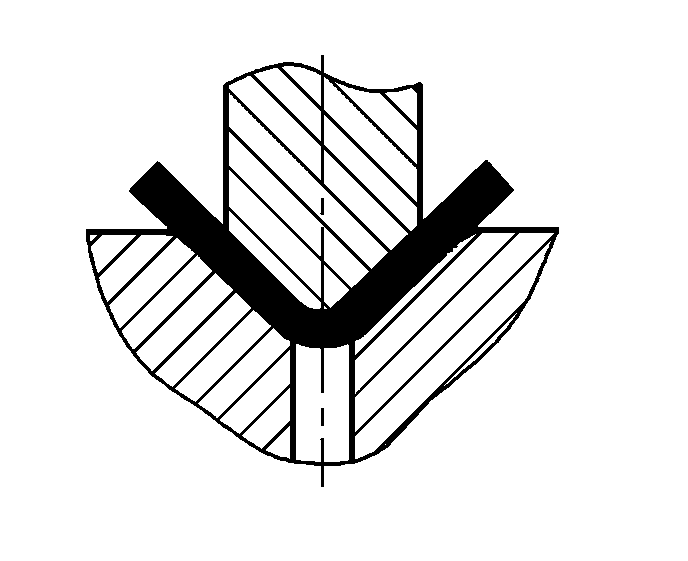
El método de plegado y la estructura de la matriz modificarán el estado de tensión de la pieza en bruto de plegado. Los distintos métodos de doblado dan lugar a presiones de doblado muy diferentes. Tomando como referencia los métodos habituales en forma de V y en forma de U piezas curvadas como ejemplos, tal y como se muestra en la Figura 1, se pueden formar mediante doblado con matrices de doblado de acero completo ordinarias, utilizando respectivamente el doblado libre, el doblado de recalcado por contacto y el doblado de corrección de impacto.
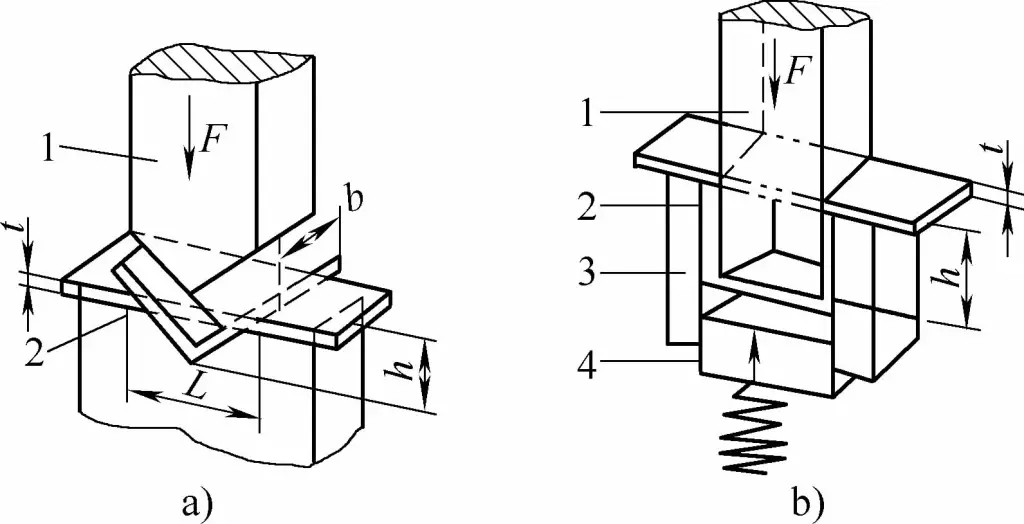
- a) Piezas de flexión en V
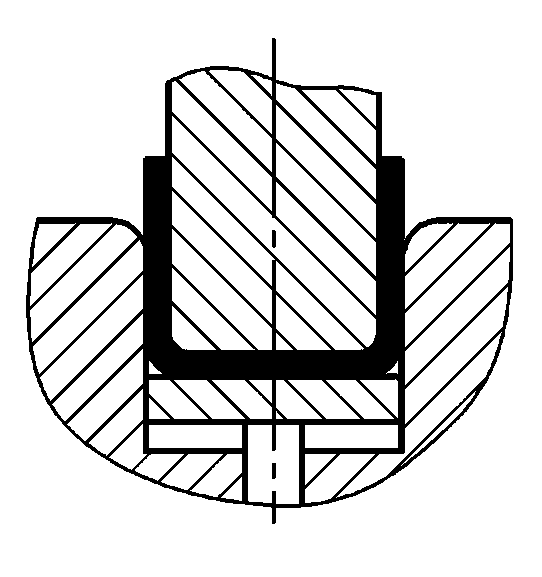
- b) Piezas de flexión en forma de U
- 1 - Punzón curvador
- 2 - Pieza de flexión
- 3 - Matriz de doblado en forma de U
- 4 - Herramienta superior
- L - Anchura de la abertura de la matriz en forma de U
- t - Espesor de la parte que se dobla
- h - Profundidad de la cavidad de la matriz de plegado en V
Las piezas curvadas en V utilizan una carga concentrada en el centro de dos soportes de una pieza en bruto plana para el curvado puro y el curvado libre, y se utilizan sobre todo en obras de construcción. En línea, las piezas curvadas de chapa de tamaño pequeño y mediano se forman sobre todo mediante curvado de recalcado por contacto, y las piezas curvadas de chapa de espesor medio de alta resistencia se curvan a menudo en prensas de fricción mediante curvado de corrección de impacto. El plegado libre requiere menos presión, sin presión adicional, sólo simple fuerza de plegado.
II. Cálculo de la fuerza de flexión mediante diversos métodos de flexión
Las fórmulas de cálculo de la fuerza de flexión mediante diversos métodos de flexión se muestran en la Tabla 1.
Tabla 1 Fórmulas de cálculo de la fuerza de flexión por diversos métodos de flexión
| Nombre | Esquema | Características de la deformación por flexión | Fórmula de cálculo de la fuerza de flexión | ||
| Teoría | Aproximadamente | Recomendado | |||
| Flexión libre de un ángulo (Pieza de flexión en forma de V) | 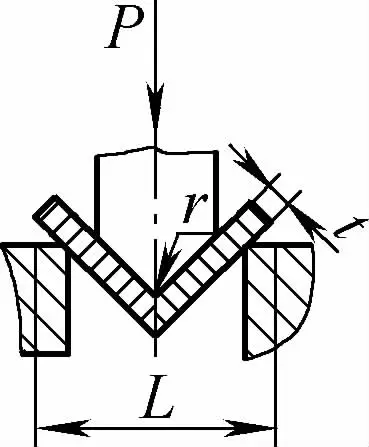 | La pieza en bruto se dobla por la mitad ejerciendo presión sobre dos soportes situados a la entrada de la matriz; la parte inferior no entra en contacto con el molde. | Cuando 2r≤L, F=0.7bt3 Rm /(r+t) Cuando 2r>L, F=2bt2 Rm /3L | F = KbtRm | F=Cbt2Rm/L |
| Flexión por contacto de ángulo único (piezas de flexión en V) | 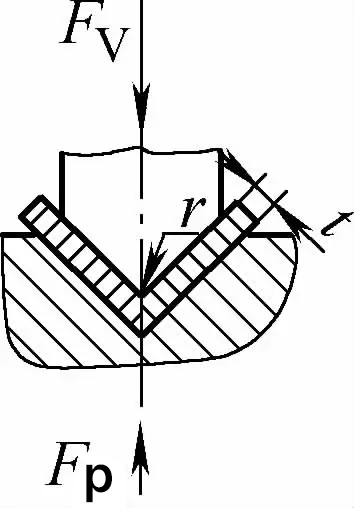 | Antes de completar el proceso de doblado, la pieza en bruto de doblado está en estrecho contacto con toda la cavidad del molde. Generalmente se utiliza una placa de presión para hacer que el doblado distancia entre troqueles mayor o igual que t | Cuando 2r≤L, Fv =0.7bt2 Rm /(r+t)+Fp Cuando 2r>L, Fv =2bt2 Rm /3L+Fp | Fv=KbtRm +Fp | Fv=2Cbt2Rm/L |
| Contacto de ángulo único con flexión de corrección de impacto (piezas de flexión en forma de V) | 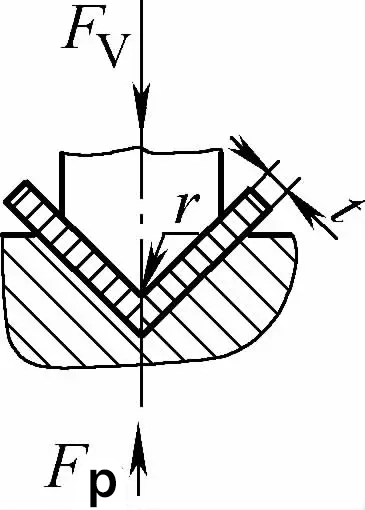 | Basada en la flexión por contacto, también tiene la función de corrección de impactos. La separación de la matriz de flexión suele ser inferior o igual a t | Fv=0.7bt2Rm/L+Fp+qAb | Fv=1,3qAb | Fv=1,39qAb |
| Flexión libre de doble ángulo (Piezas curvadas en forma de U) | 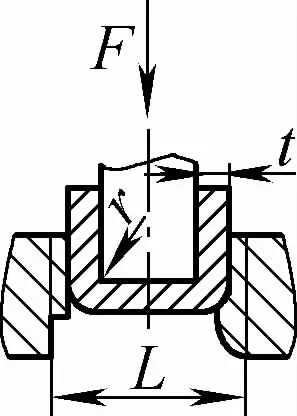 | La pieza en bruto se dobla por la mitad ejerciendo presión sobre dos soportes situados a la entrada de la matriz; la parte inferior de la pieza en bruto no entra en contacto con el molde. | Cuando 2r≤L, F=0.7bt 2 Rm /(r+t) Cuando 2r>L, F=2bt 2 Rm /3L | F =KbtRm | F=0,4CKbtRm |
| Curvado por contacto de doble ángulo (piezas curvadas en forma de U) | 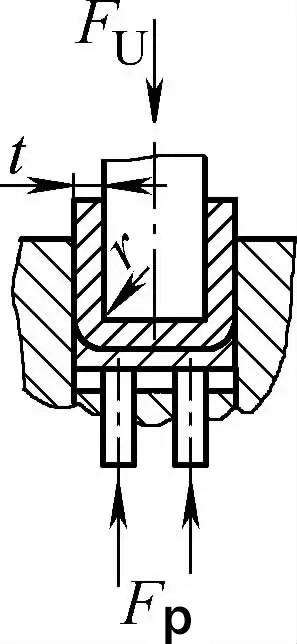 | Durante la flexión, se utiliza una placa de presión o una separación igual o ligeramente superior a t, pero no hay función de corrección de impacto | Cuando 2r≤L, Fu =0.7bt2Rm /(r+t)+Fp Cuando 2r>L, Fu =2bt2Rmn/3L+Fp | Fu =KbtRm +Fp | Fu=0,5CbtRm |
| Contacto de doble ángulo con flexión de corrección de impacto (piezas de flexión en forma de U) | 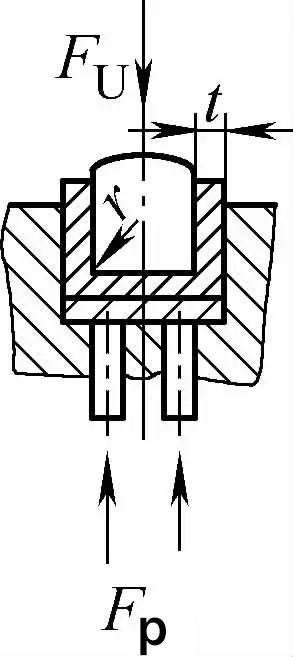 | Durante la flexión, se utiliza un espacio de flexión menor o igual a t con una placa de presión (placa superior) y también tiene la función de corrección de impacto | Fu=0.7bt2Rmn/L+Fp+qAb | Fu=1,3qAb | Fu=1,3qAb |
Nota: El significado de los símbolos de la tabla es el siguiente:
- b - anchura de la pieza de flexión (mm);
- R - resistencia a la tracción del material de la pieza de flexión (MPa);
- L - longitud de la pieza en bruto de plegado en los puntos de apoyo a ambos lados de la abertura de la matriz de plegado (mm);
- C - coeficiente, para flexión de ángulo simple L>10t, C=1; para flexión de ángulo doble r=t, C=1; n-número de ángulos de flexión (piezas);
- A - superficie de apoyo de la pieza de flexión (mm²);
- F - presión de corrección plana (kN), generalmente 30%~100% de la fuerza de flexión;
- K - coeficiente de tipo de material, el valor se puede encontrar en la Tabla 2;
- q - presión de corrección de la unidad (impacto) (MPa), el valor se puede encontrar en la Tabla 3.
Cuadro 2 Tipo de material Coeficiente Valor K
| Material | Relación L/t | |||||
| 3 | 10 | 15 | 20 | 25 | 30 | |
| 10 acero, 15 acero, latón, aluminio (blando) | 0.23 | 0.18 | 0.12 | 0.09 | 0.073 | 0.060 |
| 20 acero, 25 acero, aluminio endurecido | 0.21 | 0.17 | 0.11 | 0.08 | 0.070 | 0.057 |
| Acero 20, acero 25, acero 40, aluminio superduro | 0.20 | 0.16 | 0.10 | 0.08 | 0.065 | 0.053 |
Tabla 3 Valor aproximado de la presión de corrección unitaria (impacto) q durante la flexión (unidad: MPa)
| Material | Espesor del material a doblar t/mm | |
| ≤3 | >3~10 | |
| Aluminio | 30~40 | 50~60 |
| Latón | 60~80 | 80~100 |
| 10 acero, 15 acero, 20 acero | 80~100 | 100~120 |
| 25 acero, 30 acero, 35 acero | 100~120 | 120~150 |
Fórmulas para calcular la fuerza de flexión
Cuadro 4 Fórmulas empíricas para calcular la fuerza de flexión
| Método de plegado | Esquema | Fórmulas empíricas | Notas |
| Doblado libre | 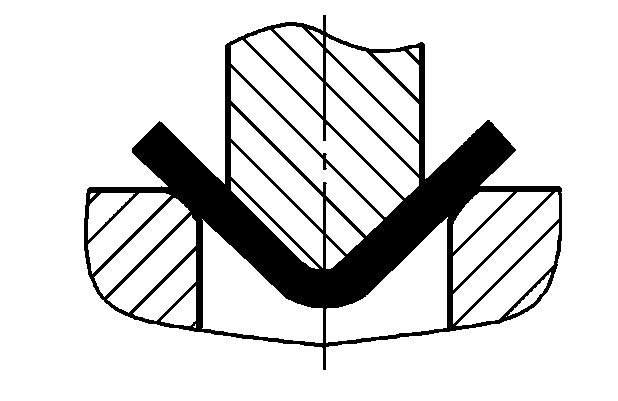 | P=(0,8Bt2σb)/(r+t) | donde P-Fuerza total de flexión (N) B-Ancho de la parte doblada (mm) t-Espesor del material (mm) σb-Resistencia a la tracción (MPa) r-Inner radio de curvatura (mm) Área de proyección de la parte de corrección A (mm)2 ) Presión de corrección unitaria (MPa), véase su valor en el cuadro 5 |
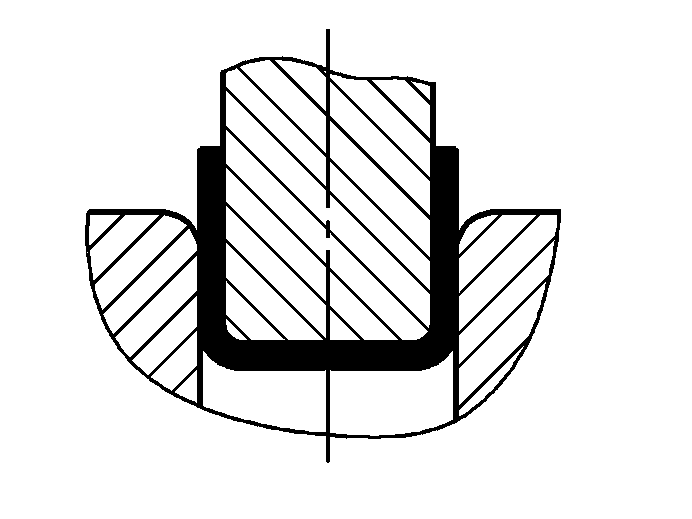 | P=(0,9Bt2σb)/(r+t) | ||
| Flexión con corrección | 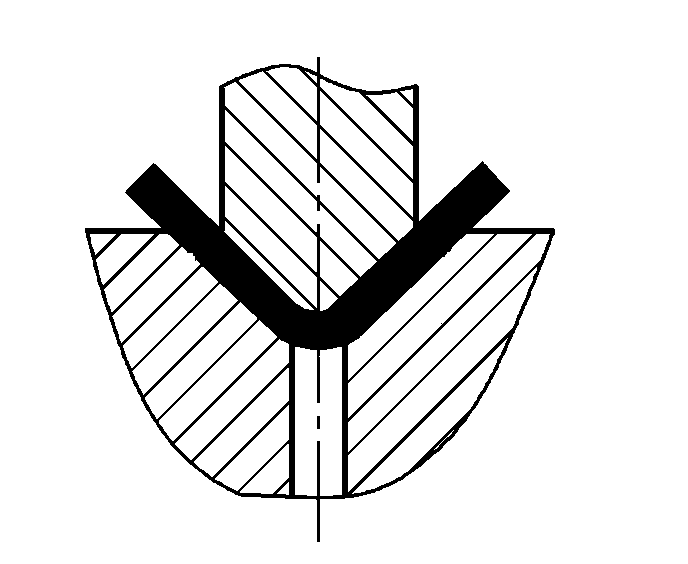 | P=(1,4Bt2σb)/(r+t) | |
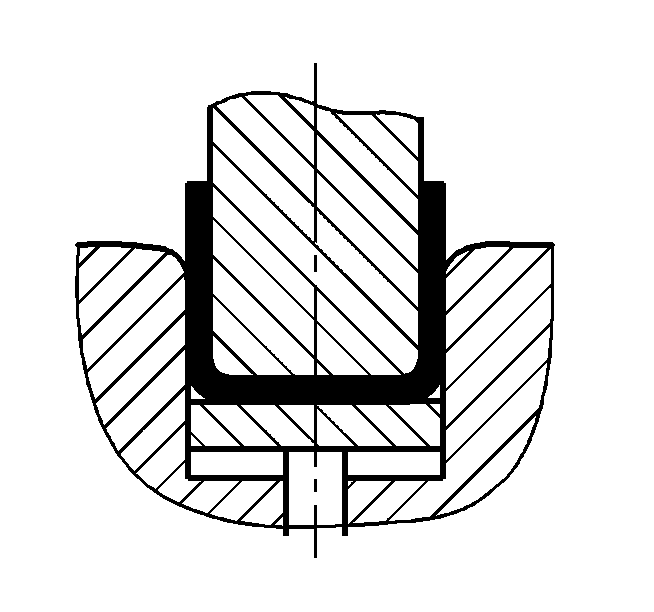 | P=(1,6Bt2σb)/(r+t) | ||
 | P=(1,4Bt2σb)/(r+t)+Aq | ||
 | P=(1,6Bt2σb)/(r+t)+Aq |
Cuadro 5 Valor q de la presión de corrección unitaria (unidad: MPa)
| Material | Espesor del material / mm | |||
| <1 | 1~3 | 3~6 | 6~10 | |
| Aluminio | 15~20 | 20~30 | 30~40 | 40~50 |
| Latón | 20~30 | 30~40 | 40~60 | 60~80 |
| 10~20 acero | 30~40 | 40~60 | 60~80 | 80~100 |
| 25~30 acero | 40~50 | 50~70 | 70~100 | 100~120 |
III. Cálculo del trabajo de flexión
El trabajo de flexión de las piezas curvadas en V puede calcularse mediante la siguiente fórmula.
Wv=mFvh
Dónde
- Wv - Trabajo de curvado de las piezas curvadas en V (J), generalmente calculado por curvado de recalcado por contacto;
- m - Coeficiente de corrección, m=0,32 para piezas de flexión en V, m=0,63 para piezas de flexión en U;
- Fv - Fuerza de flexión de las piezas de flexión en V (kN), F v o F u Para calcular la fuerza de flexión se puede encontrar la fórmula de cálculo adecuada en la Tabla 1.
- h - Profundidad de la cavidad de la matriz de plegado (es decir, carrera de plegado) (mm), h también puede calcularse mediante la siguiente fórmula.
h=0,5L~0,4(t+r)
Dónde
- L - Distancia entre los dos puntos de apoyo de las piezas de flexión en V en la abertura de la matriz de flexión (mm);
- t - Espesor de las piezas de flexión (mm);
- r - Radio de curvatura (mm).
IV. Método gráfico simplificado para la fuerza de flexión y el trabajo de flexión
La figura 2 muestra la tabla de columnas de cálculo gráfico para la fuerza de flexión y el trabajo de flexión de las piezas de flexión en forma de V y en forma de U. Esta tabla es cómoda de utilizar, el cálculo gráfico es rápido y los resultados se aproximan a la realidad, por lo que es adecuada para su uso in situ.
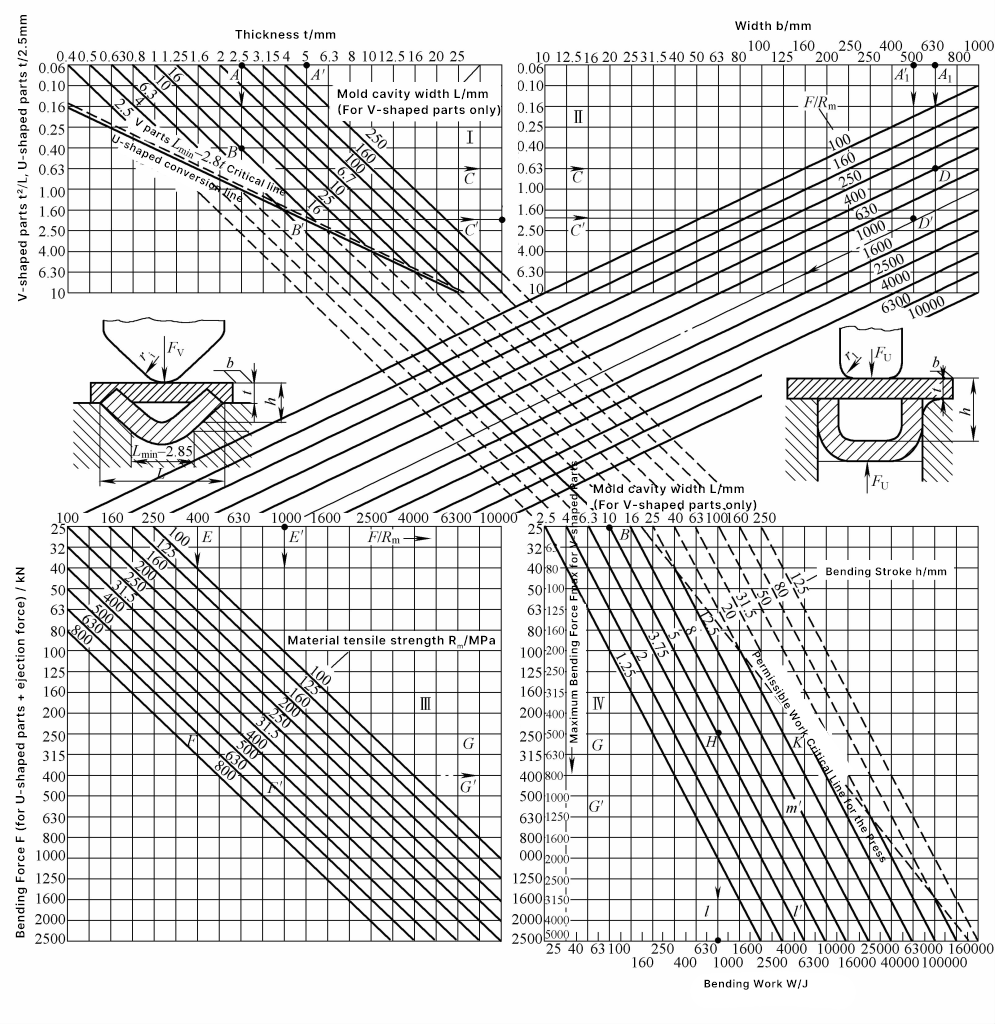
Nota: Los símbolos del gráfico significan lo siguiente:
- F - Fuerza de flexión de las piezas de flexión en V y en U (kN);
- W - Trabajo de curvado de piezas curvadas en V y en U (J);
- H - Carrera útil de curvado de las piezas curvadas en V y en U (mm);
- L, L min - Anchura de abertura de la matriz de curvar para piezas curvadas en V (mm), anchura mínima de abertura (mm);
- r - Radio de curvatura interior de las piezas de flexión (mm);
- t - Espesor de las piezas de flexión (mm).
Ejemplo de cálculo gráfico. Dada una pieza de flexión en forma de V con t=2,5mm, ancho de abertura de la matriz de flexión L=10mm. En la zona I de la figura 2, t2/L=0,63 (véase la línea ABC). Dada la anchura de la pieza de flexión b=630mm, la resistencia a la tracción del material R m =630MPa, en las zonas II y III, hallar el valor A1 DEF, y en el área III, a lo largo de la línea de extensión derecha, encontrar la línea FG, resultando una fuerza de flexión Fv =250kN.
En la zona IV, considerando la presión de enderezamiento de nivelación, la presión total es F∑ =2F=500kN. La carrera de trabajo de flexión h=0,5L=5mm, coeficiente de corrección m=0,32, por lo tanto el trabajo de flexión Wv =mF∑ h=800J, como se muestra en la línea BH y la línea CHI de la figura 2.