
Tabela de tolerâncias de dobragem
| Espessura da placa/largura da ranhura | Placa de aço laminado a frio, placa de aço galvanizado ou placa de aço revestido de zinco e alumínio | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.6 | 0.8 | 1.0 | 1.2 | 1.5 | 20 | 2.5 | 3.0 | 3.5 | .0 | 4.5 | 5.0 | Tamanho mínimo | observações | |
| V4 | 0.9 | 1.4 | 2.8 | Quando o tamanho do gráfico da peça está marcado com uma tolerância negativa, o valor da tolerância de dobragem pode ser aumentado. Por exemplo, a peça vermelha na tabela pode ser aumentada em pelo menos: 2.8:2.82,3.4:3.43 ou 3.44, 4.5:4.6, 5.5:5.6 | ||||||||||
| V6 | 1.5 | 1.7 | 2.0 | 4.5 | ||||||||||
| V7 | 1.8 | 2.1 | 2.4 | 5 | ||||||||||
| V8 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||||
| V10 | 2.1 | 2.3 | 2.7 | 7 | ||||||||||
| V12 | 2.2 | 2.5 | 2.8 | 3.4 | 8.5 | |||||||||
| V14 | 3.5 | 3.8 | 6.4 | 6.8 | 10 | |||||||||
| V16 | 3.1 | 3.8 | 4.5 | 5.0 | 11 | |||||||||
| V18 | 3.3 | 4.0 | 13 | |||||||||||
| V20 | 4.0 | 4.9 | 5.1 | 6.6 | 7.2 | 7.8 | 14 | |||||||
| V25 | 4.4 | 5.0 | 5.5 | 6.8 | 7.8 | 8.3 | 17.5 | |||||||
| V32 | 5.0 | 5.5 | 6.1 | 8.7 | ||||||||||
Flexão de dupla camada subsídio tabela
Placa de aço laminado a frio, placa de aço galvanizado ou placa de aço revestido de zinco e alumínio
| Ângulo | Largura da ranhura do molde | 90° | Ângulo de flexão interna | Ângulo de flexão externo | 180° |
|---|---|---|---|---|---|
| Espessura da placa mm | |||||
| 1.5 | V10 | 3 | 3.2 | 4.1 | 0.75 |
| 2.0 | V12 | 3.84 | 3.7 | 4.6 | 1.0 |
| 2.5 | V16 | 45 | 4.8 | 6.1 | 1.25 |
Dobragem subsídio tabela para diferentes ângulos de flexão
| Espessura da placa mm | 30 | 45° | 60° | 120° | 135 | 145° |
|---|---|---|---|---|---|---|
| 1.0 | 0.35 | 0.7 | 1.1 | 1.0 | 0.6 | 0.4 |
| 1.2 | 0.4 | 0.8 | 1.2 | 1.0 | 0.6 | 0.4 |
| 1.5 | 0.5 | 1.0 | 1.6 | 1.4 | 0.9 | 0.6 |
| 2.0 | 0.6 | 1.2 | 2.0 | 1.7 | 1.1 | 0.7 |
| 2.5 | 0.8 | 1.6 | 2.6 | 2.2 | 1.4 | 0.85 |
| 3.0 | 1.0 | 2.2 | 3.4 | 2.8 | 2.0 | 1.2 |
| 4.0 | 3.7 | 2.4 | 1.4 |
1. Exemplo de conceção de desdobramento do processo de peças
1.1 Exemplo de desenho de desdobramento do processo de dobragem de arestas em ângulo reto.
1.1.1 Exemplo de desenho de desdobramento de uma curva e fórmula de cálculo
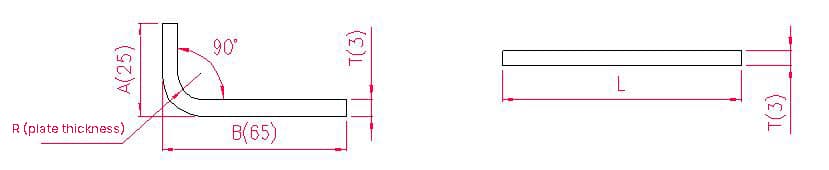
- A, B - comprimento da curvatura da peça de trabalho
- P' - margem de curvatura para a curvatura (margem de curvatura: subtrair uma margem por cada curvatura)
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L = A + B - P', ou seja, L = 25 + 65 - 5,5 = 84,5
De acordo com a Tabela 1: Para uma espessura de chapa de 3 mm, deve ser utilizada a matriz inferior V25, com uma margem de curvatura de 5,5.
Nota: De acordo com o Quadro 1, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.1.2 Exemplo de desenho de desdobramento de duas curvas e fórmula de cálculo
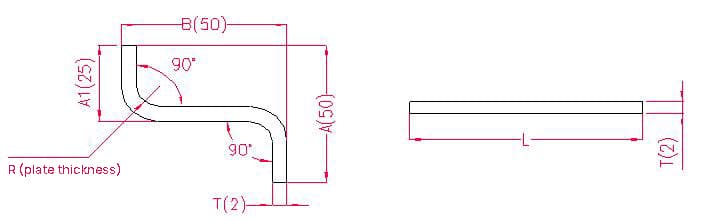
- A(A1), B - comprimento da curvatura da peça de trabalho
- P - margem de dobragem por dobragem (margem de dobragem: subtrair uma margem por cada dobragem)
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L = A + T + B - 2xP', ou seja, L = 50 + 2 + 50 - 2×3,4 = 95,6
De acordo com a Tabela 1: Para uma espessura de chapa de 2 mm, deve ser utilizado o molde inferior V12, com uma margem de curvatura de 3,4.
Nota: De acordo com o Quadro 1, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.1.3. Exemplo de desenho de desdobramento de três curvas e fórmula de cálculo
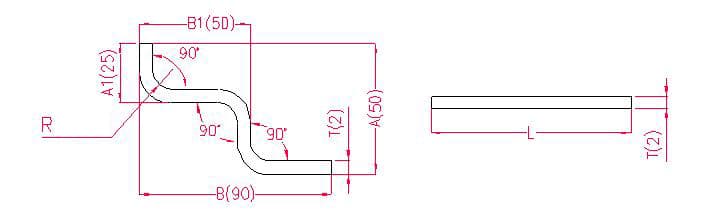
- A(A1), B(B1) - comprimento da curvatura da peça de trabalho
- P - margem de dobragem por dobragem (margem de dobragem: subtrair uma margem por cada dobragem)
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L = A + T + B + T - 3xP', ou seja, L = 50 + 2 + 90 + 2 - 3×3,4 = 133,8
De acordo com a Tabela 1: Para uma espessura de chapa de 2 mm, deve ser utilizado o molde inferior V12, com uma margem de curvatura de 3,4.
Nota: De acordo com o Quadro 1, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.1.4. Exemplo de desenho de desdobramento de quatro curvas e fórmula de cálculo
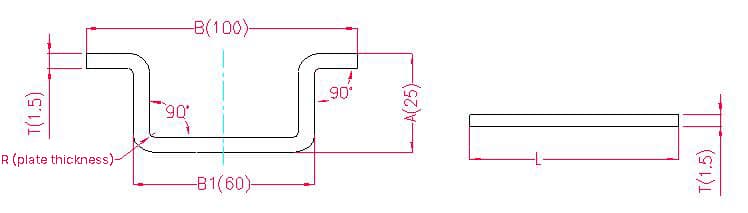
- A, B(B1) - comprimento da curvatura da peça de trabalho
- P - margem de dobragem por dobragem (margem de dobragem: subtrair uma margem por cada dobragem)
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L = A + A + B + T + T - 4xP', ou seja, L = 25 + 25 + 100 + 1,5 + 1,5 - 4×2,8 = 141,8
De acordo com a Tabela 1: Para uma espessura de chapa de 1,5 mm, deve ser utilizada a matriz inferior V12, com uma margem de curvatura de 2,8.
Nota: De acordo com o Quadro 1, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.1.5. Exemplo de desenho de desdobramento de seis curvas e fórmula de cálculo
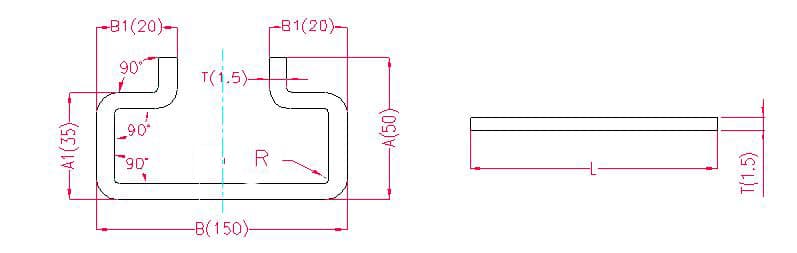
- A(A1), B(B1) - comprimento da curvatura da peça de trabalho
- P' - margem de curvatura para a curvatura (margem de curvatura: subtrair uma margem por cada curvatura)
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L = A + T + A + T + B + B1 + B1 - 6xP', ou seja, L = 50 + 1,5 + 50 + 1,5 + 150 + 20 + 20 - 6×2,8 = 276,2
De acordo com a Tabela 1: Para uma espessura de chapa de 1,5 mm, deve ser utilizada a matriz inferior V12, com uma margem de curvatura de 2,8.
Nota: De acordo com o Quadro 1, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.2.1. Exemplos e fórmulas de cálculo para o desdobramento por flexão a 180°.
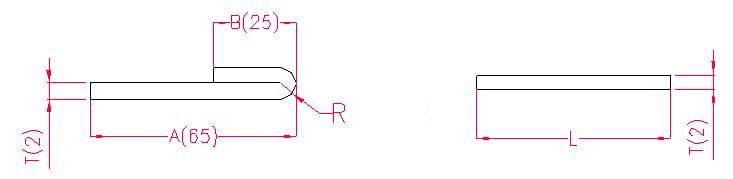
- A, B - comprimento da curvatura da peça de trabalho
- P - raio de aplanação tolerância à flexão
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L = A + B - P', ou seja, L = 25 + 65 - 1 = 89
De acordo com a Tabela 2: Para uma espessura de placa de 2 mm, deve ser utilizada a matriz inferior V12, com uma margem de curvatura de metade da espessura da placa.
Nota: De acordo com o Quadro 2, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
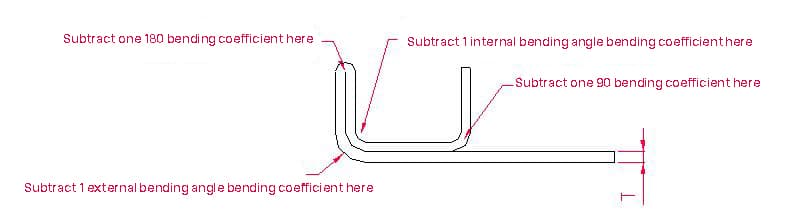
1.2.2. Exemplos e fórmulas de cálculo para o desdobramento por flexão de camada dupla.
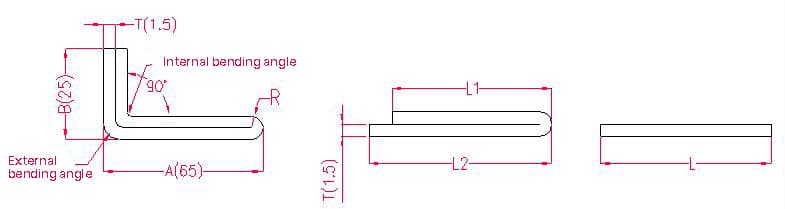
- A, B - comprimento da curvatura da peça de trabalho
- P1 - tolerância à flexão para os cantos internos
- P2 - tolerância à flexão para os cantos exteriores
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L1 = (A-1,5) + (B-1,5) - P1, ou seja, L1 = (65-1,5) + (25-1,5) - 3,2 = 83,8
L2 = A + B - P2, ou seja, L2 = 65 + 25 - 4,1 = 85,9
L = L1 + L2 - T/2, ou seja, L = 83,8 + 85,9 - 0,75 = 168,95
De acordo com a Tabela 2: Para uma espessura de placa de 1,5 mm, deve ser utilizado o molde inferior V12, com uma tolerância de dobragem de 3,2 para os cantos internos, 4,1 para os cantos externos e 0,75 para um ângulo de 180°.
Nota: De acordo com o Quadro 2, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.2.3. Exemplos e fórmulas de cálculo para o desdobramento por flexão de camada dupla.
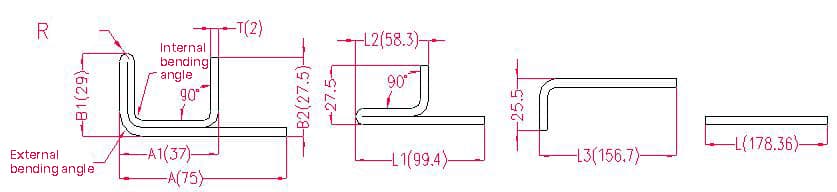
- A(A1), B1B2- comprimento da curvatura da peça de trabalho
- P1 - tolerância à flexão do ângulo interno
- P2 - tolerância à flexão para o ângulo externo
- P3 - Tolerância de flexão de 90°
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
- P4 - Tolerância de curvatura de 180°
Comprimento de desdobramento: L1 = A + B1 - P2, ou seja, L1 = 75 + 29 - 4,6 = 99,4
L2 = (A1 - T) + (B1 - T) - P1, ou seja, L2 = (37 - 2) + (29 - 2) - 3,7 = 58,7
L3 = L1 + L2 - P3, ou seja, L3 = 99,4 + 58,3 - 1 = 156,7
L = 25,5 + L3 - P1, ou seja, L = 25,5 + 156,7 - 3,84 = 178,36
De acordo com o Quadro 2: Para uma espessura de chapa de 1,5 mm, deve ser utilizado o molde inferior V12, com uma tolerância de dobragem de ângulo interno de 3,2, uma tolerância de dobragem de ângulo externo de 4,1 e uma tolerância de dobragem de 180° de 0,75.
Nota: De acordo com o Quadro 2, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.2.4. Exemplos e fórmulas de cálculo para o desdobramento por flexão de camada dupla.
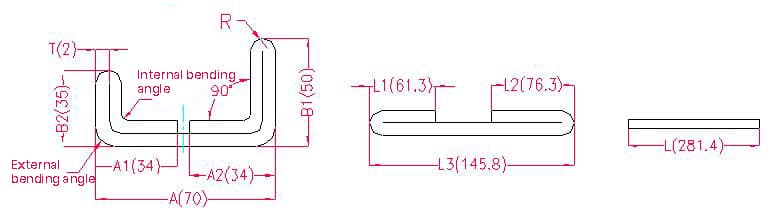
- A, A1, A2, B1, B2, L, L1, L2, L3 - comprimento da curvatura da peça de trabalho
- P1 - tolerância à flexão do ângulo interno
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
- P2 - tolerância à flexão para o ângulo externo
Comprimento de desdobramento: L1 = (A1-T) + (B2-T) - P1, ou seja, L1 = (35-2) + (34-2) - 3,7 = 61,3
L2 = (B1-T) + (A2-T) - P1, ou seja, L2 = (50-2) + (34-2) - 3,7 = 76,3
L3 = A + B1 + B2 - 2 x P2, ou seja, L3 = 70 + 35 + 50 - 2 x 4,6 = 145,8
L = L1 + L2 + L3 - 2 x P3, ou seja, L = 61,3 + 75,3 + 145,8 - 2 x 1 = 281,4
De acordo com o Quadro 2: Para uma espessura de placa de 2 mm, deve ser utilizado o molde inferior V12, com uma tolerância de dobragem de ângulo interno de 3,7, uma tolerância de dobragem de ângulo externo de 4,6 e uma tolerância de dobragem de 180° de 1.
Nota: De acordo com o Quadro 2, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.3.1. Exemplos e fórmulas de cálculo para a dobragem de ângulos especiais Desdobramento.
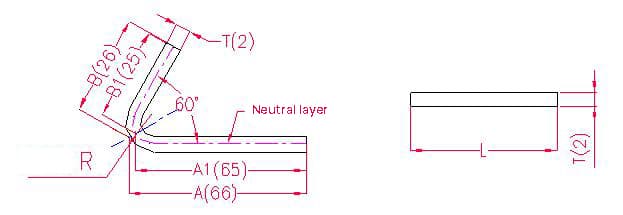
- A(A1), B(B1) - comprimento da curvatura da peça de trabalho
- P - tolerância de curvatura para um ângulo de curvatura (varia consoante o ângulo)
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L = (A-T) + (B-T) - P' = A1 + B1 - P', ou seja, L = (66-1) + (26-1) - 2 = 65+25-2 = 88
De acordo com a Tabela 3: Para uma espessura de placa de 2 mm, deve ser utilizado o molde inferior V12, e a tolerância de flexão para um ângulo de 60° é de 2.
Nota: De acordo com o quadro 3, a camada neutra deve ser utilizada como comprimento e largura de flexão.
1.3.2. Exemplos e fórmulas de cálculo para o desdobramento por pressão por etapas.
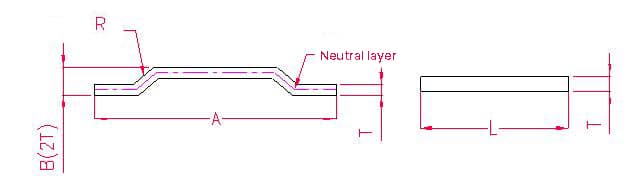
- A, B - comprimento da curvatura da peça de trabalho
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L = A + 1
Nota: Quando o degrau é igual a duas espessuras de placa, adicionar 0,5 para cada degrau, e adicionar 1 para dois degraus.
1.3.3. Exemplos e fórmulas de cálculo para desdobramento de ângulos especiais.
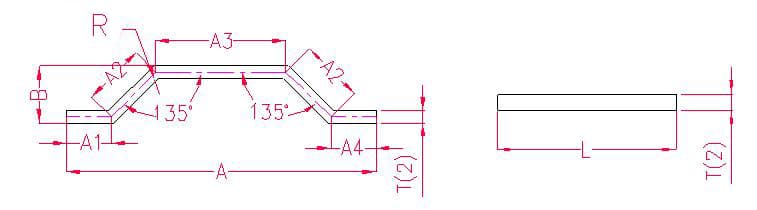
- A(A1A2A3A4), B - comprimento da curvatura da peça de trabalho
- P - tolerância de flexão para um ângulo de 135
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Comprimento de desdobramento: L = A1 + A2 + A3 + A2 + A4 - P - P
Nota: Para dobrar com degraus, basta subtrair duas folgas.
De acordo com a Tabela 3: Para uma espessura de placa de 2 mm, deve ser utilizado o molde inferior V12, e a tolerância de flexão para um ângulo de 135° é de 1,1.
1.3.4. Exemplos e fórmulas de cálculo para desdobramento de ângulos especiais.
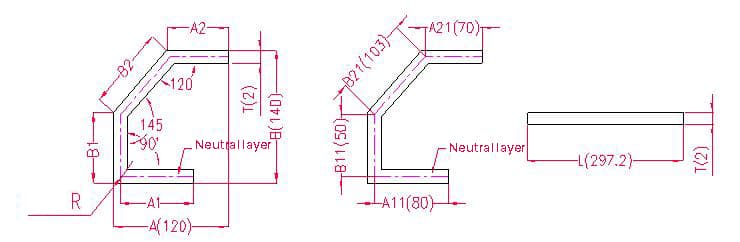
- A(A1A2), B(B1B2) - comprimento da curvatura da peça de trabalho
- P1 - tolerância de flexão para um ângulo de 120°
- P2 - tolerância de flexão para um ângulo de 145
- P3 - Tolerância de flexão de 90°
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
Nota: Quando a dimensão é marcada no contorno, tem de ser convertida para o tamanho da camada neutra ao calcular o comprimento de desdobramento.
Comprimento de desdobramento: L = A11 + B11 + B21 + A21 - P1 - P2 - P3, ou seja, L = 80 + 50 + 103 + 70 - 1,7 - 0,7 - 3,4 = 297,2
De acordo com o Quadro 3: Para uma espessura de placa de 2 mm, deve ser utilizado o molde inferior V12, com uma tolerância de flexão de 1,7 para um ângulo de 120°, 0,7 para um ângulo de 145° e 3,4 para um ângulo de 90°.
Nota: De acordo com o Quadro 3, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.4.1. Exemplos e fórmulas de cálculo para o desdobramento flangeado ordinário.
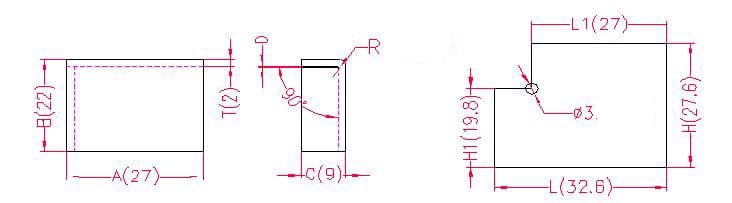
- A, B, C - comprimento, largura e altura da curvatura da peça de trabalho
- P - tolerância à flexão
- R - raio de curvatura (normalmente igual à espessura da placa)
- H(H1), L(L1) - comprimento de desdobramento de cada lado
- T - espessura do material
- D - intervalo do processo de flexão (normalmente entre 0 e 0,5)
Comprimento de desdobramento: L1 = A, ou seja, L1 = 27
L = A + C - P, ou seja, L = 27 + 9 - 3,4 = 32,6
H1 = B - T - D, ou seja, H1 = 22 - 2 - 0,2 = 19,8 (Nota: D é tomado como 0,2)
H = B + C - P, ou seja, H = 22 + 9 - 3,4 = 27,6
De acordo com a Tabela 1: Para uma espessura de chapa de 2 mm, deve ser utilizado o molde inferior V12, com uma margem de curvatura de 3,4.
Nota: De acordo com o Quadro 1, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.4.2. Exemplos e fórmulas de cálculo para o desdobramento de portas comuns.
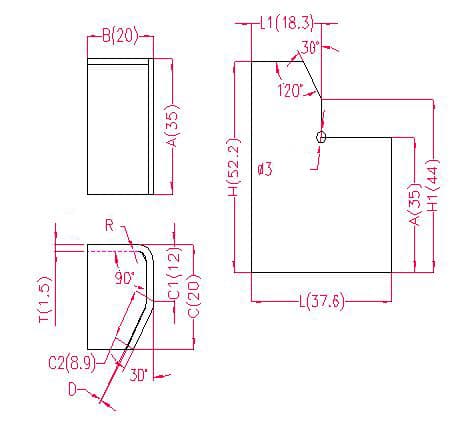
- A, B, C - comprimento, largura e altura da curvatura da peça de trabalho
- L(L1), H(H1) - comprimento de desdobramento de cada lado
- P - tolerância de flexão para um ângulo de 90
- P1 - tolerância de flexão para um ângulo de 30°
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
- D - intervalo do processo de flexão (normalmente entre 0 e 0,5)
Comprimento de desdobramento: L1 = B - T - D, ou seja, L1 = 20 - 1,5 - 0,2 = 18,3
L = B + C1 + C2 - P - P1, ou seja, L = 20 + 12 + 8,9 - 2,8 - 0,5 = 37,6
H1 = C1 + A - P - D, ou seja, H1 = 12 + 35 - 2,8 - 0,2 = 44 (Nota: D é tomado como 0,2)
H = A + C - P, ou seja, H = 35 + 20 - 2,8 = 52,2
De acordo com a Tabela 1: Para uma espessura de placa de 1,5 mm, deve ser utilizado o molde inferior V12, com uma tolerância de dobragem de 2,8 para um ângulo de 90° e de 0,5 para um ângulo de 30°.
Nota: De acordo com o Quadro 1, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.
1.4.3. Exemplos e fórmulas de cálculo para a dobragem e desdobragem por flangeamento normal.
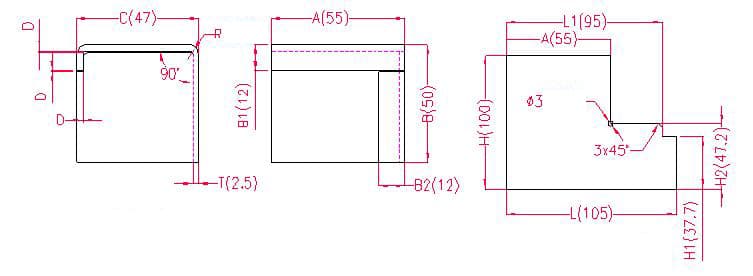
- A, B, C - comprimento, largura e altura da curvatura da peça de trabalho
- P - tolerância à flexão
- R - raio de curvatura (normalmente igual à espessura da placa)
- T - espessura do material
- D - intervalo do processo de flexão (normalmente entre 0 e 0,5)
Comprimento de desdobramento: H1 = B - B1 - D, ou seja, H1 = 50 - 12 - 0,3 = 37,7 (Nota: D é considerado como 0,2)
H2 = B - T - D, ou seja, H2 = 50 - 2,5 - 0,3 = 47,2
H = B + C + B1 - 2xP, ou seja, H = 50 + 47 + 12 - 2×4,5 = 100
L1 = A + C - T - D - P, ou seja, L1 = 55 + 47 - 2,5 - 0,3 - 4,5 = 94,7
L = A + C+ B2 - 2xP, ou seja, L = 55 + 47 + 12 - 2×4,5 = 105
De acordo com a Tabela 1: Para uma espessura de chapa de 2,5 mm, deve ser utilizada a matriz inferior V16, com uma margem de curvatura de 4,5.
Nota: De acordo com o Quadro 1, diferentes matrizes inferiores têm diferentes tolerâncias de flexão e diferentes espessuras de chapa têm diferentes tolerâncias de flexão.









