Bei der Erstellung der Zeichnung für die Entwicklung von Blechbauteilen müssen auch die Auswirkungen der Dicke des zu verarbeitenden Materials berücksichtigt werden, d. h. es müssen entsprechende Anpassungen der Blechdicke vorgenommen werden.
Im Allgemeinen ist bei Blechmaterialien mit einer Dicke von weniger als 3 mm keine Anpassung der Blechdicke erforderlich. Sie kann nach dem zentralen Durchmesser des Blechmaterials oder nach den Schnittlinien der Innen- und Außenfläche berechnet werden. Die Abmessungen nach der Umformung liegen innerhalb des zulässigen Abweichungsbereichs. Wenn die Blechdicke größer als 3 mm ist, sollte sie nach dem mittleren Durchmesser des Blechmaterials berechnet werden. Zur Vereinfachung der Beschreibung beziehen sich die Berechnungen für die folgenden entwickelten Materialien auf den zentralen Durchmesser des Blechmaterials.
1. Entwicklungsberechnung von zylindrischen Schalen
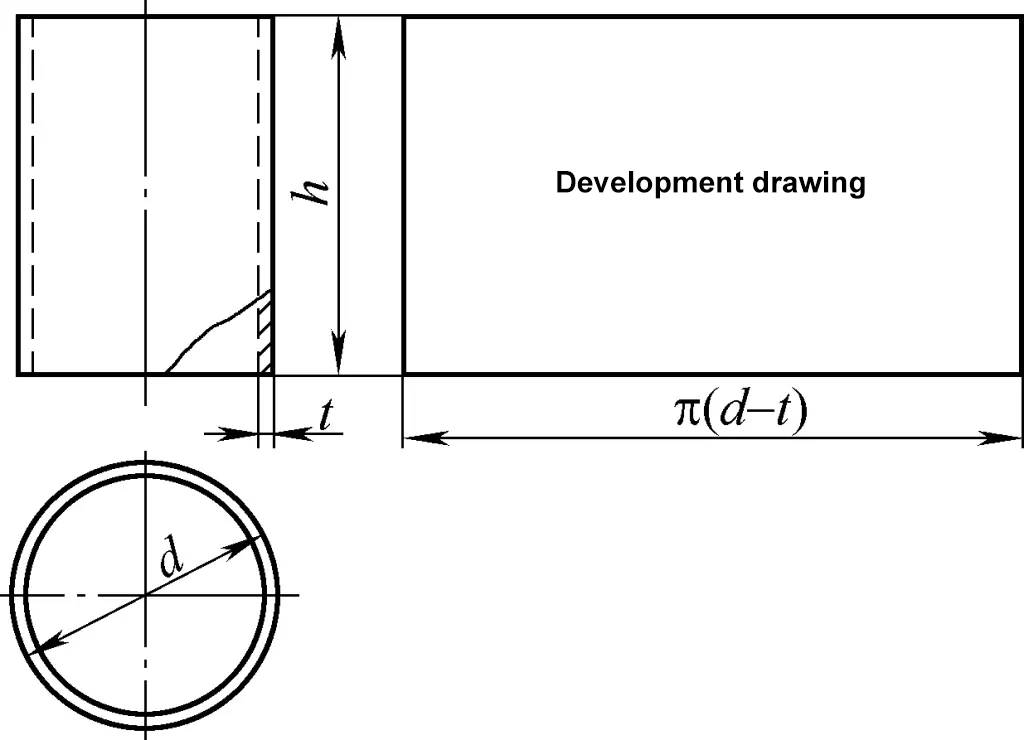
Die zylindrische Schale gehört zur zylindrischen Oberfläche, und ihre Entwicklungszeichnung ist ein Rechteck. Eine Seite des Rechtecks entspricht dem Umfang des Zylinders π(d-t), und die andere Seite ist die Höhe h des Zylinders, wie in Abbildung 1 dargestellt. In der Abbildung ist d der Außendurchmesser des Zylinders und t die Blechdicke.
2. Entwicklungsberechnung von rechtwinkligen Kegeln
Die Entwicklungszeichnung des rechten Kreiskegels ist ein Sektorbogen. Die Berechnungsformel für die in Abbildung 2 dargestellte Entwicklungszeichnung des rechten Kreiskegels lautet:
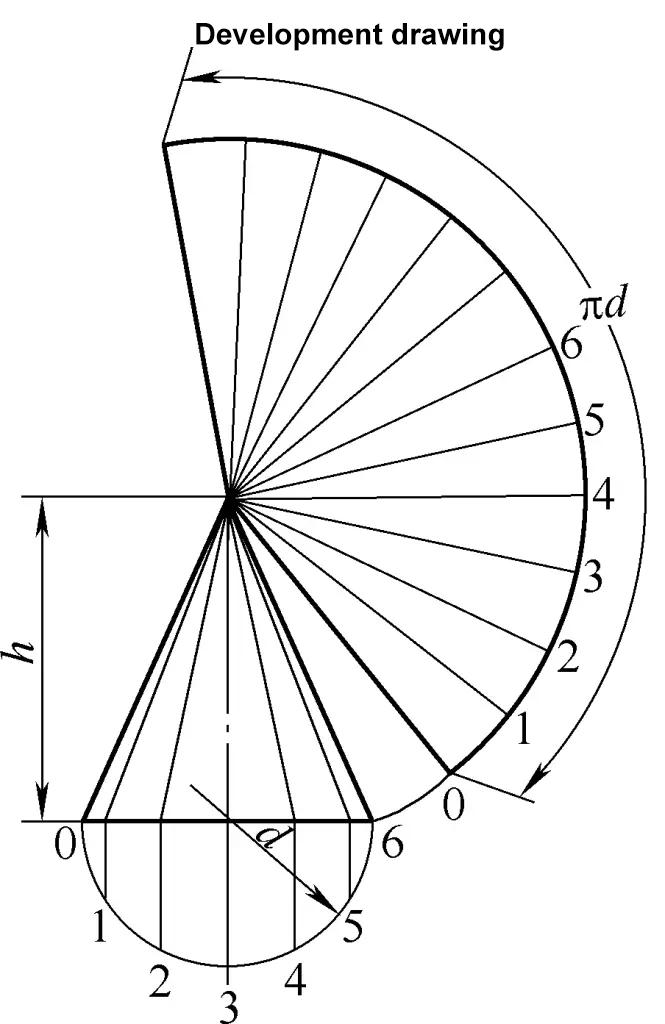
R=1/2√(d2+4h2)
α=180d/R
L=2Rsinα/2
In der Formel
- R - Radius des Sektorbogens (mm);
- α - Sektorwinkel (°);
- L - Sehnenlänge des Sektorbogens (mm).
3. Entwicklungsberechnung von rechtwinkligen Kegelstümpfen
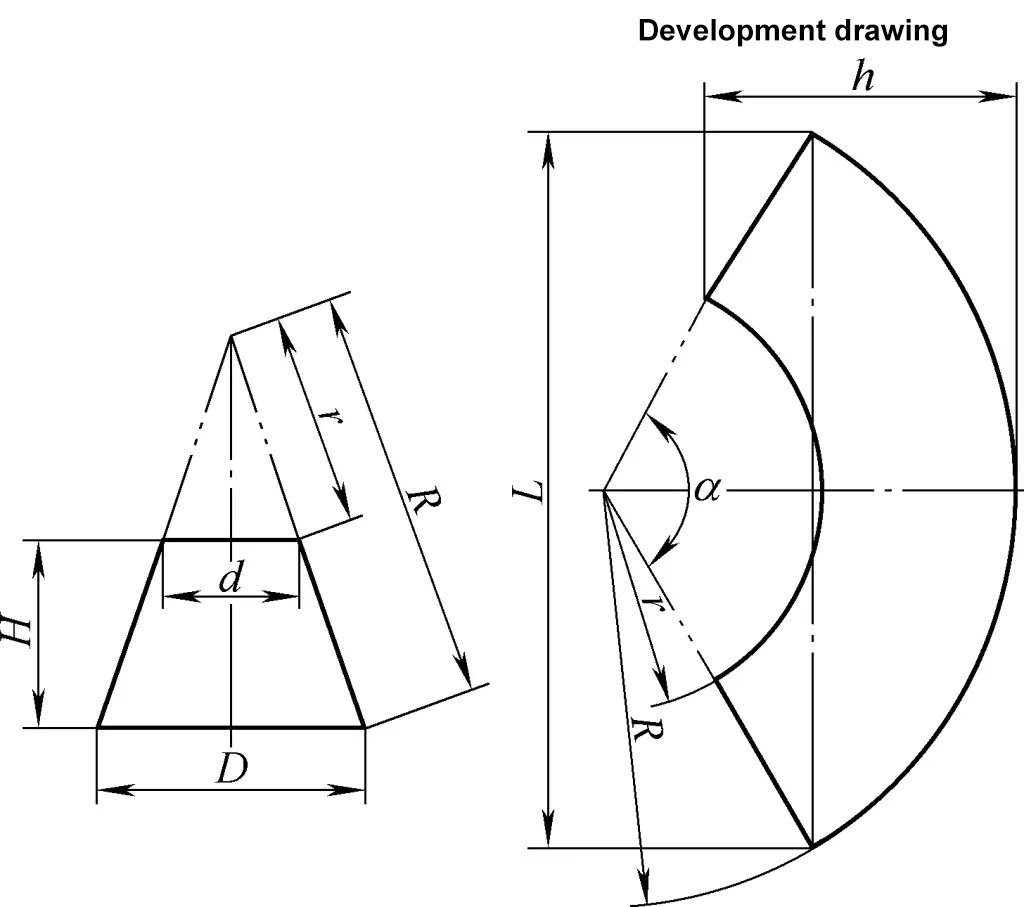
Die Abwicklungszeichnung des rechten Kreiskegelstumpfes ist ein konzentrischer Sektorbogen. Die Berechnungsformel für die Entwicklungszeichnung des rechten Kreiskegelstumpfes in Abbildung 3 lautet:
R=√{(D/2)2+[DH/(D-d)]2}
r=dR/D
α=180d/r
L=2Rsinα/2
h=R-rcosα/2
Wenn α>180°, h=R+rsin[(α-180)/2]
Die Bedeutung der Symbole in der Formel finden Sie in Abbildung 3.
4. Entwicklungsberechnung von schrägen, rechtwinkligen Kegeln
Die Entwicklungszeichnung des schrägen rechten Kreiskegels ist ein unregelmäßiger Sektorbogen. Die Berechnungsformel für die Entwicklungszeichnung des schrägen rechten Kreiskegels in Abbildung 4 lautet:
tanβ1=h/[1/2(D1-d1)+l]
tanβ2=h/[1/2(d1-D1)+l]
D=D1-t/2 (sinβ1+ sinβ2)
d=d1-t/2 (sinβ1+ sinβ2)
A=Dl/(D-d)
H=Ah/l
fn=√[(A-D/2cosαn)2+(D/2)2Sünde2αn+H2]
yn=fn(1-h/H)
m=Dsin(180°/n )
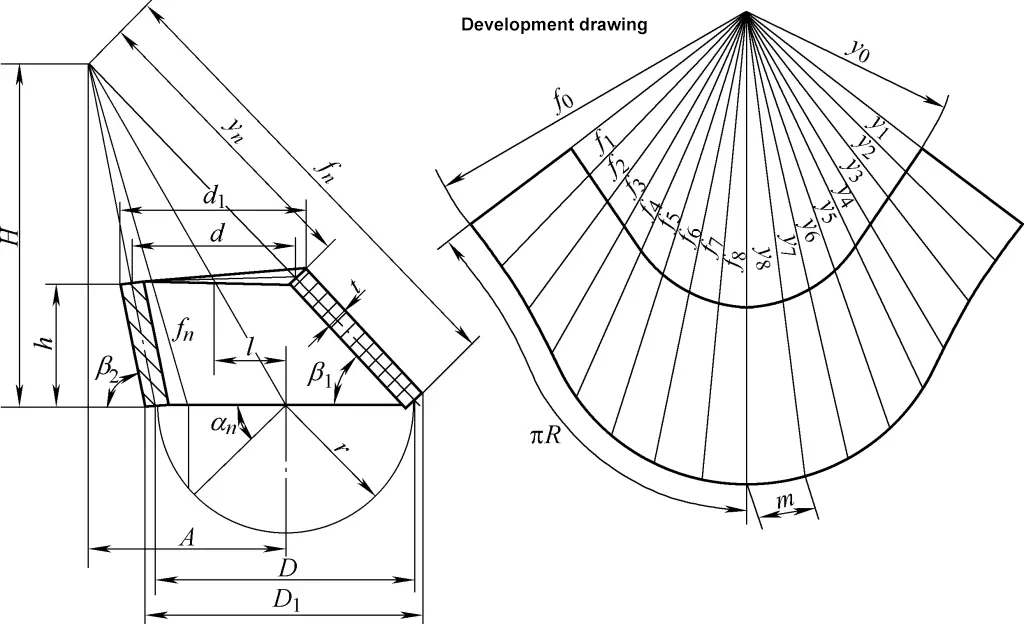
In der Formel
- D1, d1 - Außendurchmesser des großen und des kleinen Endes (mm);
- D, d - Mitteldurchmesser des großen und des kleinen Endes (mm);
- h - Zentrale Höhe (mm);
- l - Exzenterabstand (mm);
- n - Anzahl der Teilungen des Umfangs; je höher die Anzahl der Teilungen, desto komplexer die Berechnung, aber desto genauer die Zeichnung. Im Allgemeinen kann die Anzahl der Teilungen in Tabelle 1 angegeben werden;
- fn, yn - Längen der schrägen Linien des schrägen rechten Kreiskegels (mm).
Tabelle 1 Anzahl der Abteilungen für Entwicklungen im Bereich Blech
| Radius des abgewickelten Stücks/mm | Anzahl der Abteilungen |
| Innerhalb von 50 | 8 |
| 50~150 | 12 |
| 150~250 | 16 |
| 250~400 | 24 |
| 400~650 | 32 |
| 650~1000 | 48 |
| 1000~2000 | 64 |
| Über 2000 | 96 |
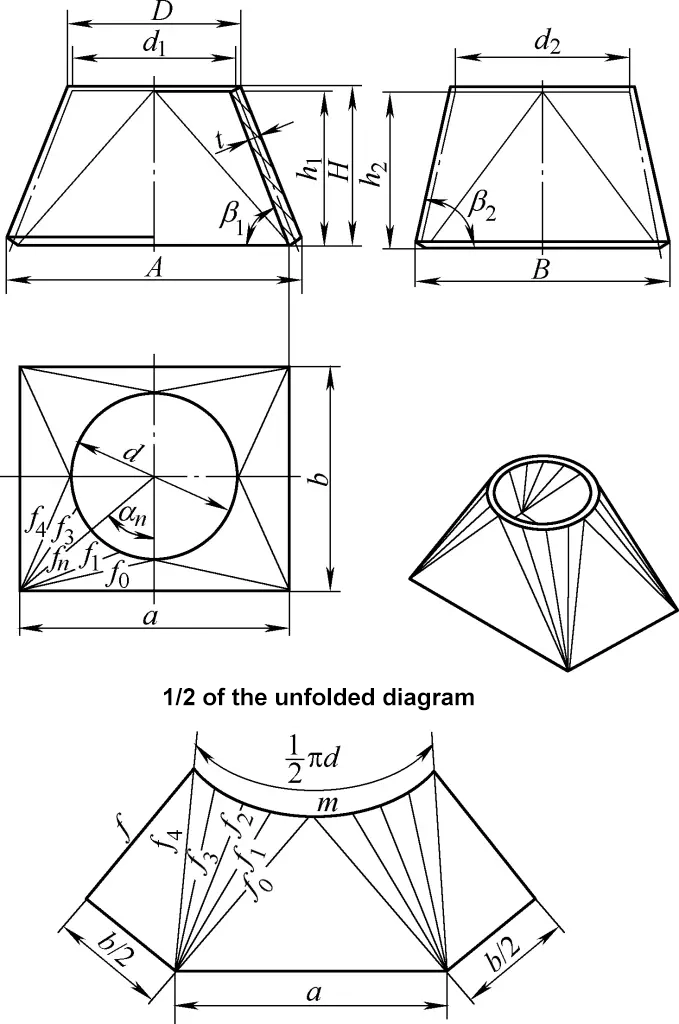
5. Entwicklungsberechnung des orthokonischen Übergangskanals von rechteckig zu rund
Der in Abbildung 5 dargestellte orthokonische rechteckige bis runde Übergangskanal besteht aus vier gleichen schrägen rechtwinkligen Kegelflächen und vier symmetrischen Dreiecksebenen. Die Berechnungsformel für seine Entwicklungszeichnung lautet:
tanβ1=2H/(A-D)
tanβ2=2H/(B-D)
d1=D-tsinβ1
d2=D-tsinβ2
d=1/2(d1+d2)=D-t/2(sinβ1+sinβ2)
a=A-2tsinβ1
b=B-2tsinβ2
h1=H-t/2cosβ1
h2=H-t/2cosβ2
h=1/2(h1+h2)=H-t/4(cosβ1+cosβ2)
f0=1/2√[a2+(b-d2)2+4h22]
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h2(wenn 0<α<90°)
fn=1/2√(a-dsinαn)2+(b-dcosαn)2+4h12(wenn α=90°)
f=1/2√[(a-d)2+4h12]
m=πd/n
Die Bedeutung der Symbole in der Formel ist Abbildung 5 zu entnehmen, und n ist die Anzahl der Teilungen des Umfangs. Im Allgemeinen kann die Anzahl der Teilungen in Tabelle 1 die Berechnungsanforderungen erfüllen.