Die Biegekraft ist eine wichtige Grundlage für die Gestaltung von Stanzprozessen, die Auswahl von Pressen und die Konstruktion von Werkzeugen.
Da die Größe der Biegekraft nicht nur von der Größe des Rohlings, den mechanischen Eigenschaften des Materials, dem Abstand zwischen den Stützen der Matrize, dem Biegeradius und dem Abstand zwischen den Formen abhängt, sondern auch stark von der Biegemethode, ist es schwierig, genaue Berechnungen mit theoretischen Analysemethoden durchzuführen. Daher werden in der Produktion normalerweise die in Tabelle 1 aufgeführten empirischen Formeln für eine grobe Berechnung der Biegekraft verwendet.
I. Theoretische Berechnungsgrundlagen und Methoden für die Biegekraft
Die theoretische Berechnungsmethode der Biegekraft wird unter der statischen Gleichgewichtsbedingung abgeleitet, dass die Summe der verschiedenen äußeren Kräfte, die auf den Biegerohling einwirken, gleich Null ist, und dass das äußere Drehmoment, das auf den Biegerohling einwirkt, gleich seinem inneren Widerstandsdrehmoment ist, durch konventionelle Berechnung.
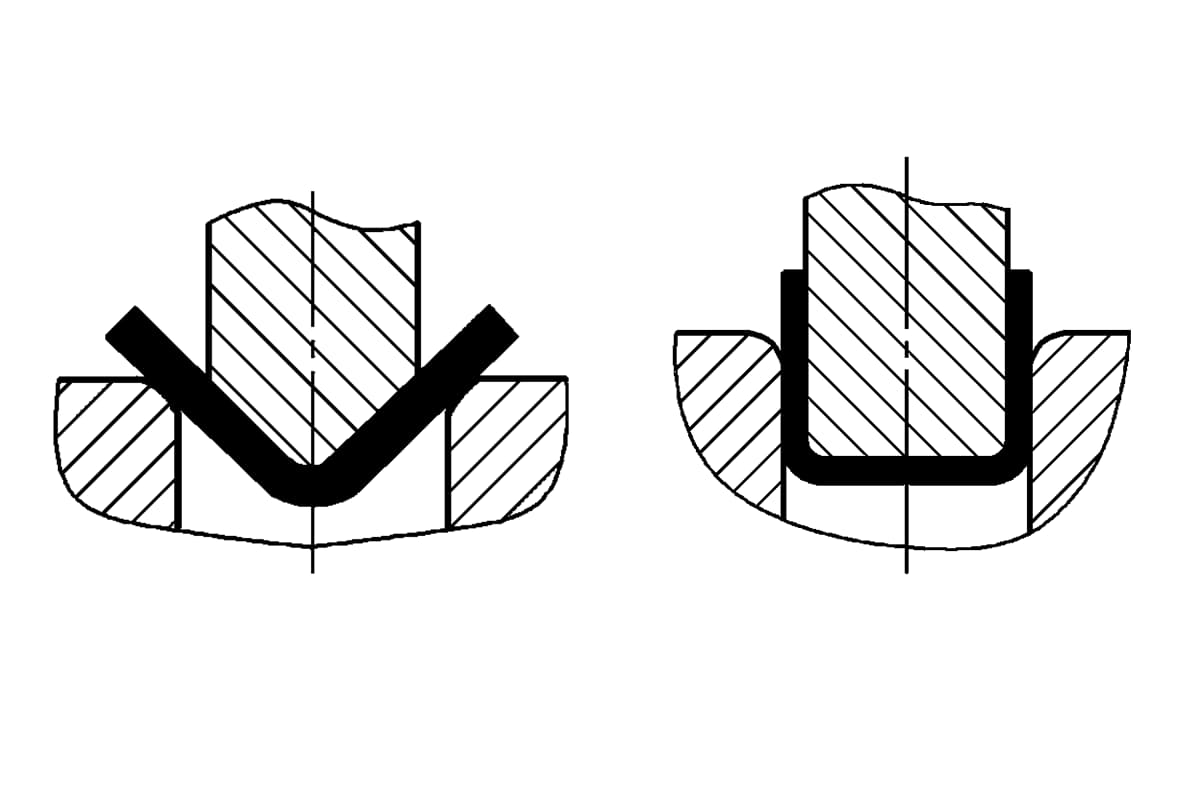
Die Biegemethode und die Werkzeugstruktur verändern den Spannungszustand des Biegerohlings. Verschiedene Biegeverfahren führen zu sehr unterschiedlichen Biegedrücken. Nehmen wir die üblicherweise verwendeten V- und U-förmigen Biegeteile wie in Abbildung 1 dargestellt, können sie durch Biegen mit gewöhnlichen Vollstahl-Biegewerkzeugen bzw. durch freies Biegen, Kontaktstauchen und Schlagkorrekturbiegen geformt werden.
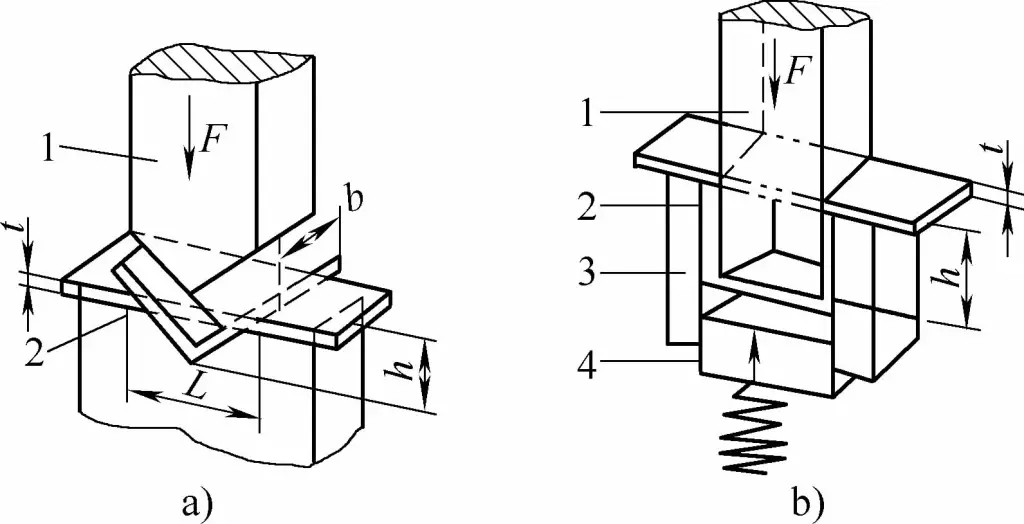
- a) V-förmige Biegeteile
- b) U-förmige Biegeteile
- 1 - Biegestempel
- 2 - Biegeteil
- 3 - U-förmige Biegematrize
- 4 - Oberes Werkzeug
- L - Breite der U-förmigen Matrizenöffnung
- t - Dicke des Biegeteils
- h - Tiefe des V-förmigen Biegestempelhohlraums
Bei V-förmigen Biegeteilen wird eine konzentrierte Last in der Mitte von zwei Stützen eines flachen Rohlings für reines Biegen und freies Biegen verwendet, die meist auf Baustellen eingesetzt werden. Online werden kleine und mittelgroße Blechbiegeteile meist durch Kontaktstauchen geformt, und hochfeste, mitteldicke Blechbiegeteile werden häufig auf Reibungspressen durch Schlagkorrekturbiegen gebogen. Das freie Biegen erfordert weniger Druck, ohne zusätzlichen Druck, nur mit einfacher Biegekraft.
II. Berechnung der Biegekraft mit verschiedenen Biegemethoden
Die Berechnungsformeln für die Biegekraft bei verschiedenen Biegemethoden sind in Tabelle 1 aufgeführt.
Tabelle 1 Berechnungsformeln für die Biegekraft bei verschiedenen Biegemethoden
| Name | Schematische Darstellung | Merkmale der Biegeverformung | Formel zur Berechnung der Biegekraft | ||
| Theoretisch | Ungefähr | Empfohlen | |||
| Freie Biegung mit einem Winkel (V-förmiges Biegeteil) | 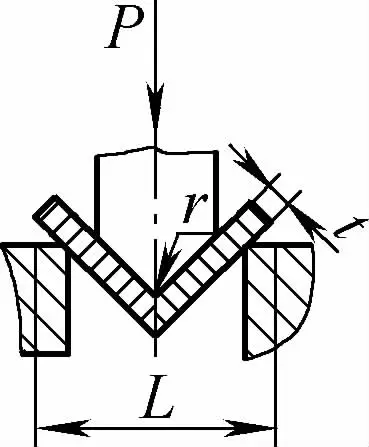 | Der Rohling wird in der Mitte nach unten gebogen, indem Druck auf zwei Stützen am Werkzeugeingang ausgeübt wird, wobei der untere Teil die Form nicht berührt. | Wenn 2r≤L, F=0,7bt3 Rm /(r+t) Wenn 2r>L, F=2bt2 Rm /3L | F = KbtRm | F=Cbt2Rm/L |
| Einwinkelige Kontaktbiegung (V-förmige Biegeteile) | 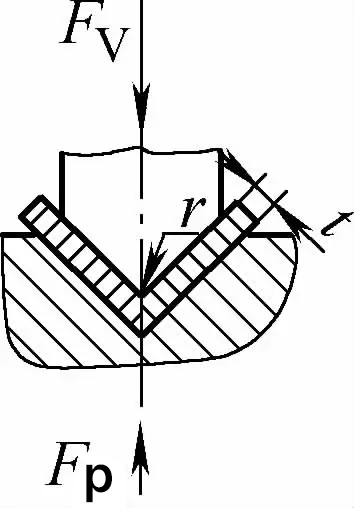 | Bevor der Biegevorgang abgeschlossen ist, befindet sich der Biegerohling in engem Kontakt mit dem gesamten Formhohlraum. Im Allgemeinen wird eine Druckplatte verwendet, um die Biegung Düsenspalt größer als oder gleich t | Wenn 2r≤L, Fv =0,7bt2 Rm /(r+t)+Fp Wenn 2r>L, Fv =2bt2 Rm /3L+Fp | Fv=KbtRm +Fp | Fv=2Cbt2Rm/L |
| Ein-Winkel-Kontakt mit Stoßkorrekturbiegung (V-förmige Biegeteile) | 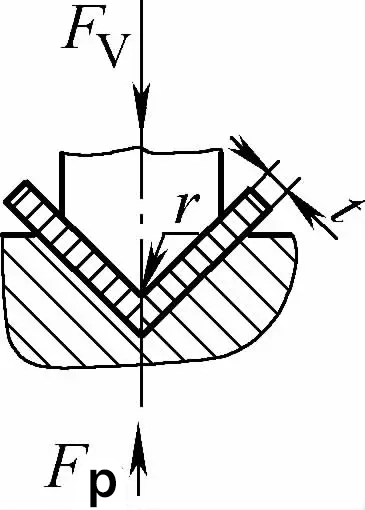 | Auf der Grundlage des Kontaktbiegens hat es auch die Funktion der Stoßkorrektur. Der Biegestempelabstand ist im Allgemeinen kleiner oder gleich t | Fv=0,7bt2Rm/L+Fp+qAb | Fv=1,3qAb | Fv=1,39qAb |
| Doppelt gewinkeltes freies Biegen (U-förmige Biegeteile) | 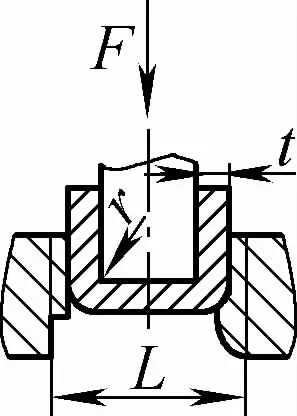 | Der Biegerohling wird in der Mitte gebogen, indem Druck auf zwei Stützen am Gesenkeingang ausgeübt wird, wobei der untere Teil des Rohlings die Form nicht berührt. | Wenn 2r≤L, F=0,7bt 2 Rm /(r+t) Wenn 2r>L, F=2bt 2 Rm /3L | F =KbtRm | F=0,4CKbtRm |
| Doppelwinkel-Kontaktbiegen (U-förmige Biegeteile) | 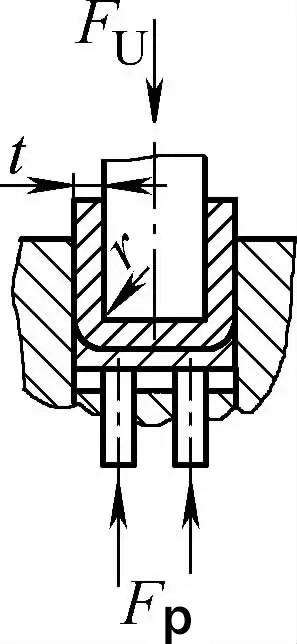 | Beim Biegen wird eine Druckplatte verwendet oder ein Spalt, der gleich oder etwas größer als t ist, aber es gibt keine Stoßkorrekturfunktion | Wenn 2r≤L, Fu =0,7bt2Rm /(r+t)+Fp Wenn 2r>L, Fu =2bt2Rmn/3L+Fp | Fu =KbtRm +Fp | Fu=0,5CbtRm |
| Doppelwinkelkontakt mit Stoßkorrekturbiegung (U-förmige Biegeteile) | 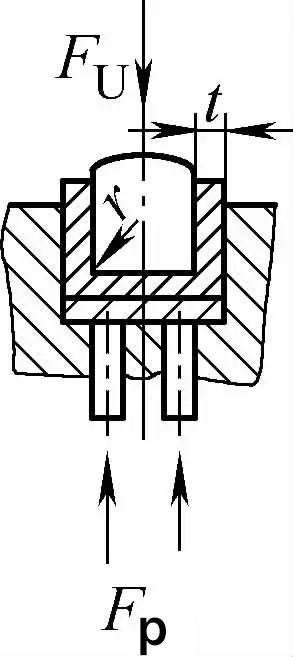 | Beim Biegen wird ein Biegespalt kleiner oder gleich t mit einer Druckplatte (Oberplatte) verwendet und hat auch die Funktion der Stoßkorrektur | Fu=0,7bt2Rmn/L+Fp+qAb | Fu=1,3qAb | Fu=1,3qAb |
Hinweis: Die Bedeutung der Symbole in der Tabelle ist wie folgt:
- b - Breite des Biegeteils (mm);
- R - Zugfestigkeit des Materials des Biegeteils (MPa);
- L - Länge des Biegerohlings an den Auflagepunkten auf beiden Seiten der Biegestempelöffnung (mm);
- C - Koeffizient, für einwinklige Biegung L>10t, C=1; für zweiwinklige Biegung r=t, C=1; n-Anzahl der Biegewinkel (Stücke);
- A - Auflagefläche des Biegeteils (mm²);
- F - flacher Korrekturdruck (kN), im Allgemeinen 30%~100% der Biegekraft;
- K - Materialtypkoeffizient, der Wert ist in Tabelle 2 zu finden;
- q - Einheit (Aufprall) Korrekturdruck (MPa), der Wert ist in Tabelle 3 zu finden.
Tabelle 2 Materialtyp Koeffizient K-Wert
| Material | Verhältnis L/t | |||||
| 3 | 10 | 15 | 20 | 25 | 30 | |
| 10 Stahl, 15 Stahl, Messing, Aluminium (weich) | 0.23 | 0.18 | 0.12 | 0.09 | 0.073 | 0.060 |
| 20 Stahl, 25 Stahl, gehärtetes Aluminium | 0.21 | 0.17 | 0.11 | 0.08 | 0.070 | 0.057 |
| 20 Stahl, 25 Stahl, 40 Stahl, superhartes Aluminium | 0.20 | 0.16 | 0.10 | 0.08 | 0.065 | 0.053 |
Tabelle 3 Näherungswert des Einheits-(Schlag-)Korrekturdrucks q beim Biegen (Einheit: MPa)
| Material | Dicke des Biegematerials t/mm | |
| ≤3 | >3~10 | |
| Aluminium | 30~40 | 50~60 |
| Messing | 60~80 | 80~100 |
| 10 Stahl, 15 Stahl, 20 Stahl | 80~100 | 100~120 |
| 25 Stahl, 30 Stahl, 35 Stahl | 100~120 | 120~150 |
Formeln zur Berechnung der Biegekraft
Tabelle 4 Empirische Formeln zur Berechnung der Biegekraft
| Biegeverfahren | Schematische Darstellung | Empirische Formeln | Anmerkungen |
| Freies Biegen | 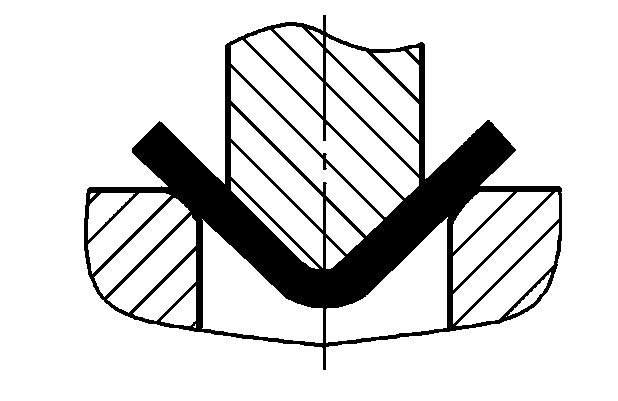 | P=(0,8Bt2σb)/(r+t) | wobei P-Gesamte Biegekraft (N) B-Breite des gebogenen Teils (mm) t-Materialstärke (mm) σb-Zugfestigkeit (MPa) r-Innenseite Biegeradius (mm) A-Korrekturteil Projektionsfläche (mm)2 ) Einheit Korrekturdruck (MPa), Wert siehe Tabelle 5 |
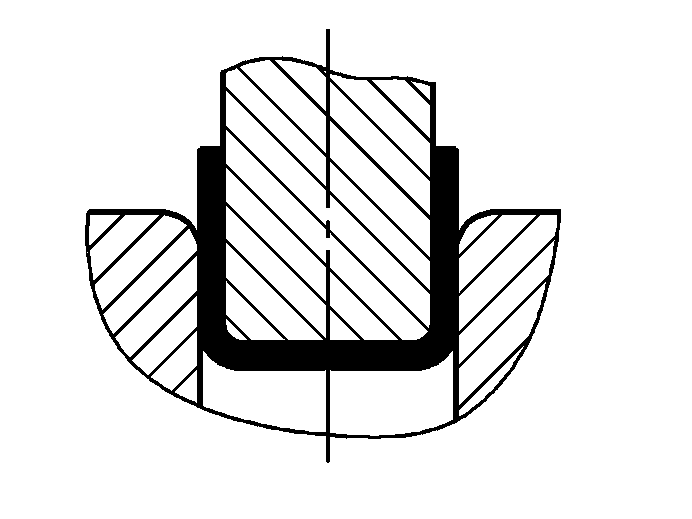 | P=(0,9Bt2σb)/(r+t) | ||
| Biegen mit Korrektur | 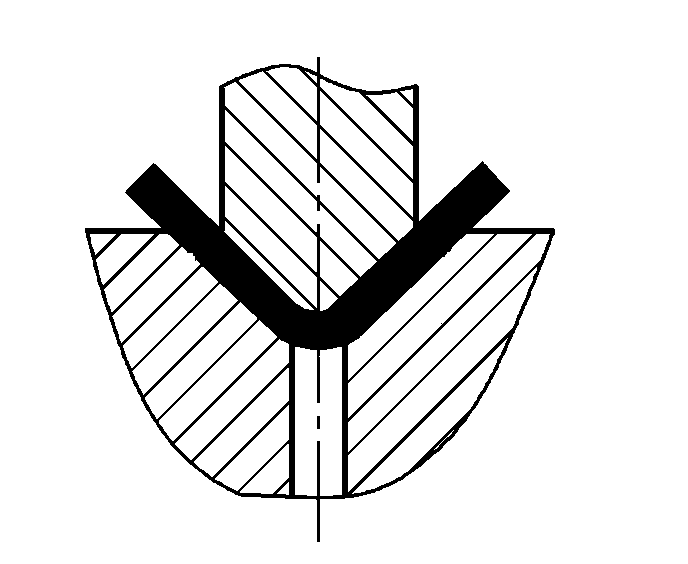 | P=(1,4Bt2σb)/(r+t) | |
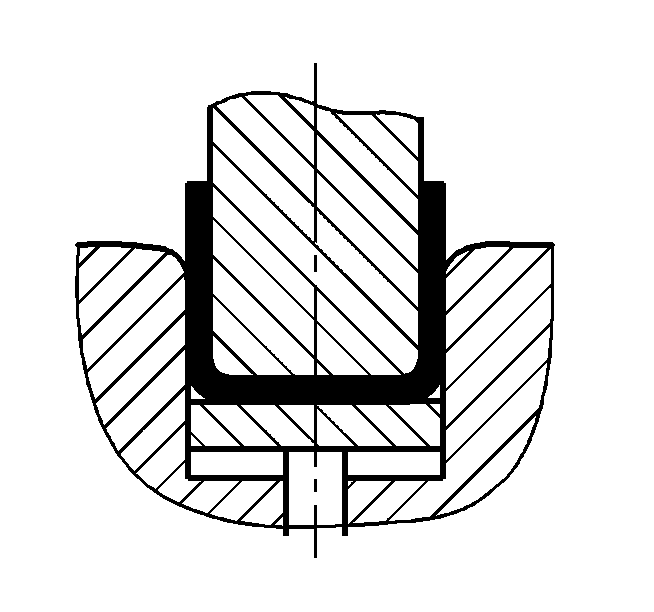 | P=(1,6Bt2σb)/(r+t) | ||
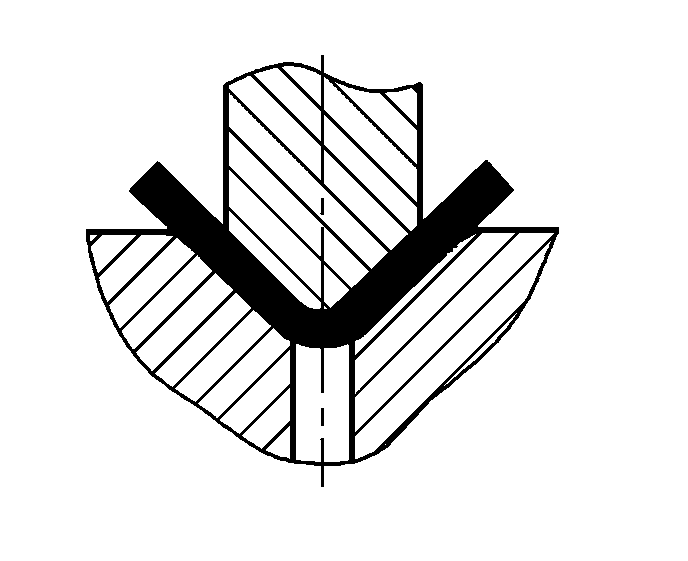 | P=(1,4Bt2σb)/(r+t)+Aq | ||
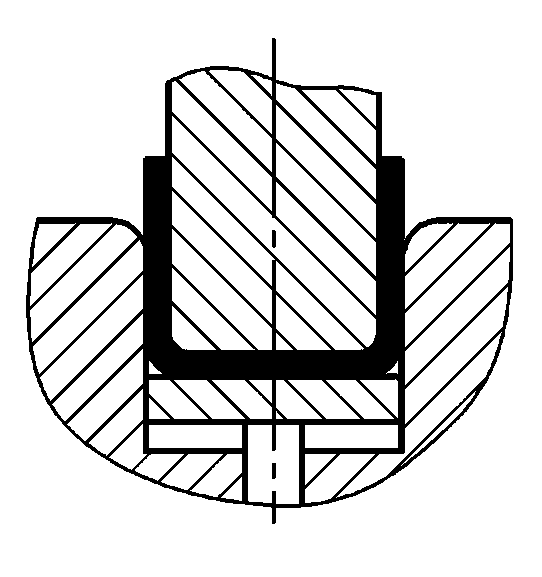 | P=(1,6Bt2σb)/(r+t)+Aq |
Tabelle 5 Einheitskorrekturdruck q-Wert (Einheit: MPa)
| Material | Materialstärke / mm | |||
| <1 | 1~3 | 3~6 | 6~10 | |
| Aluminium | 15~20 | 20~30 | 30~40 | 40~50 |
| Messing | 20~30 | 30~40 | 40~60 | 60~80 |
| 10~20 Stahl | 30~40 | 40~60 | 60~80 | 80~100 |
| 25~30 Stahl | 40~50 | 50~70 | 70~100 | 100~120 |
III. Berechnung der Biegearbeit
Die Biegearbeit von V-förmigen Biegeteilen kann mit der folgenden Formel berechnet werden.
Wv=mFvh
Wo
- Wv - Biegearbeit von V-förmigen Biegeteilen (J), im Allgemeinen berechnet durch Kontaktstauchbiegen;
- m - Korrekturkoeffizient, m=0,32 für V-förmige Biegeteile, m=0,63 für U-förmige Biegeteile;
- Fv - Biegekraft der V-förmigen Biegeteile (kN), F v oder F u Für die Berechnung der Biegekraft kann die entsprechende Berechnungsformel in Tabelle 1 gefunden werden.
- h - Tiefe des Biegestempelhohlraums (d.h. Biegehub) (mm), h kann auch mit der folgenden Formel berechnet werden.
h=0,5L~0,4(t+r)
Wo
- L - Abstand zwischen den beiden Auflagepunkten der V-förmigen Biegeteile an der Öffnung der Biegematrize (mm);
- t - Dicke der Biegeteile (mm);
- r - Biegeradius (mm).
IV. Vereinfachte grafische Methode für Biegekraft und Biegearbeit
Abbildung 2 zeigt das grafische Säulendiagramm zur Berechnung der Biegekraft und Biegearbeit von V- und U-förmigen Biegeteilen. Dieses Diagramm ist bequem zu verwenden, die grafische Berechnung ist schnell und die Ergebnisse sind realitätsnah und für den Einsatz vor Ort geeignet.
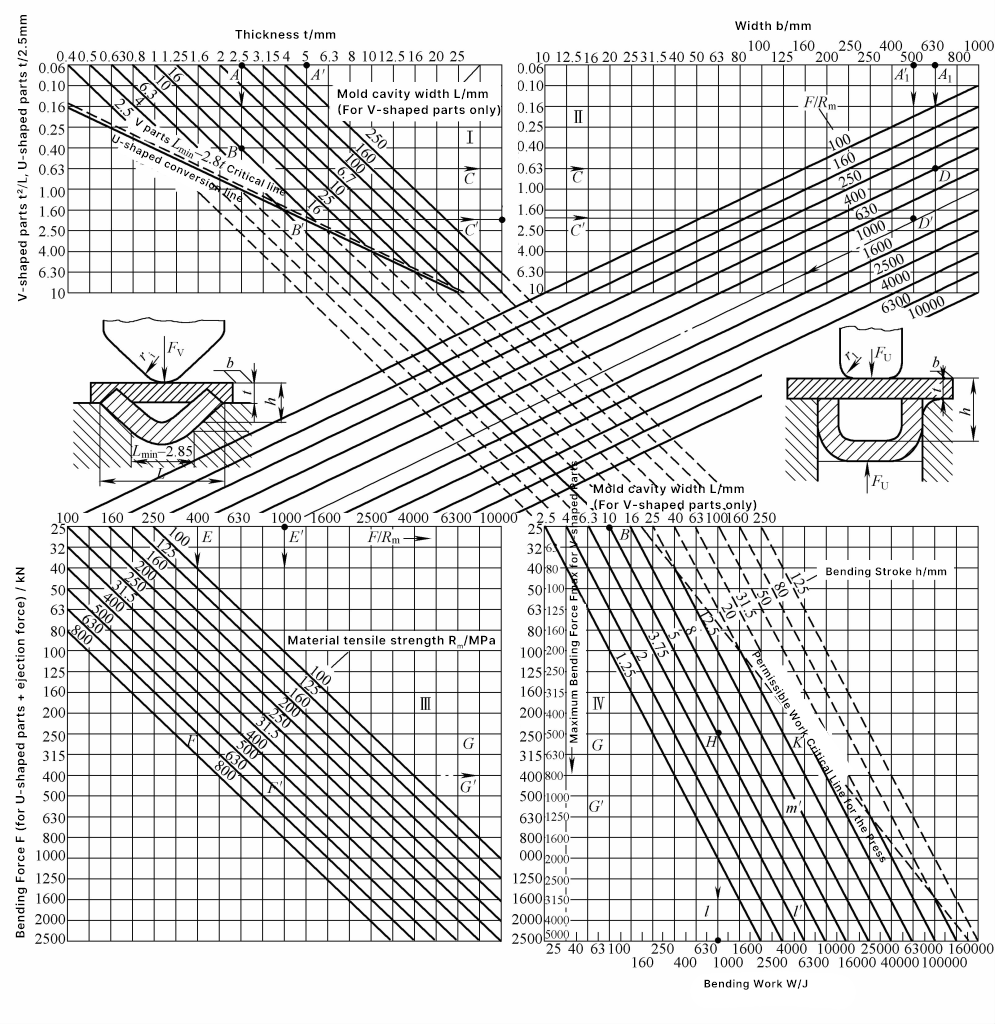
Hinweis: Die Symbole in der Tabelle haben folgende Bedeutung:
- F - Biegekraft der V- und U-förmigen Biegeteile (kN);
- W - Biegearbeit von V- und U-förmigen Biegeteilen (J);
- H - Biegearbeitshub von V- und U-förmigen Biegeteilen (mm);
- L, L min - Öffnungsweite der Biegematrize für V-förmige Biegeteile (mm), Mindestöffnungsweite (mm);
- r - Innerer Biegeradius der Biegeteile (mm);
- t - Dicke der Biegeteile (mm).
Grafisches Berechnungsbeispiel. Gegeben sei ein V-förmiges Biegeteil mit t=2,5mm, Öffnungsweite des Biegewerkzeugs L=10mm. Im Bereich I der Abbildung 2, t2/L=0,63 (siehe ABC-Linie). Bei der Breite des Biegeteils b=630mm, der Zugfestigkeit des Materials R m =630MPa, in den Bereichen II und III, die A1 DEF-Linie und im Bereich III entlang der rechten Verlängerungslinie die FG-Linie finden, woraus sich eine Biegekraft Fv =250kN.
Im Bereich IV beträgt der Gesamtdruck unter Berücksichtigung des Nivellierungsrichtdrucks F∑ =2F=500kN. Der Biegearbeitshub h=0,5L=5mm, Korrekturkoeffizient m=0,32, also die Biegearbeit Wv =mF∑ h=800J, wie in der BH-Linie und der CHI-Linie in Abbildung 2 dargestellt.