Tabla de margen de plegado
| Espesor de la chapa/Anchura de la ranura | Chapa de acero laminada en frío, chapa de acero galvanizada o chapa de acero con revestimiento de aluminio zincado | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.6 | 0.8 | 1.0 | 1.2 | 1.5 | 20 | 2.5 | 3.0 | 3.5 | .0 | 4.5 | 5.0 | Tamaño mínimo | observaciones | |
| V4 | 0.9 | 1.4 | 2.8 | Cuando el tamaño gráfico de la pieza está marcado con una tolerancia negativa, se puede aumentar el valor de la tolerancia de plegado. Por ejemplo, la pieza roja de la tabla puede aumentarse como mínimo: 2,8:2,82,3,4:3,43 ó 3,44, 4,5:4,6, 5,5:5,6 | ||||||||||
| V6 | 1.5 | 1.7 | 2.0 | 4.5 | ||||||||||
| V7 | 1.8 | 2.1 | 2.4 | 5 | ||||||||||
| V8 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||||
| V10 | 2.1 | 2.3 | 2.7 | 7 | ||||||||||
| V12 | 2.2 | 2.5 | 2.8 | 3.4 | 8.5 | |||||||||
| V14 | 3.5 | 3.8 | 6.4 | 6.8 | 10 | |||||||||
| V16 | 3.1 | 3.8 | 4.5 | 5.0 | 11 | |||||||||
| V18 | 3.3 | 4.0 | 13 | |||||||||||
| V20 | 4.0 | 4.9 | 5.1 | 6.6 | 7.2 | 7.8 | 14 | |||||||
| V25 | 4.4 | 5.0 | 5.5 | 6.8 | 7.8 | 8.3 | 17.5 | |||||||
| V32 | 5.0 | 5.5 | 6.1 | 8.7 | ||||||||||
Flexión de doble capa subsidio tabla
Chapa de acero laminada en frío, chapa de acero galvanizada o chapa de acero con revestimiento de aluminio zincado
| Ángulo | Anchura de la ranura del molde | 90° | Ángulo de flexión interno | Ángulo de flexión exterior | 180° |
|---|---|---|---|---|---|
| Espesor de la placa mm | |||||
| 1.5 | V10 | 3 | 3.2 | 4.1 | 0.75 |
| 2.0 | V12 | 3.84 | 3.7 | 4.6 | 1.0 |
| 2.5 | V16 | 45 | 4.8 | 6.1 | 1.25 |
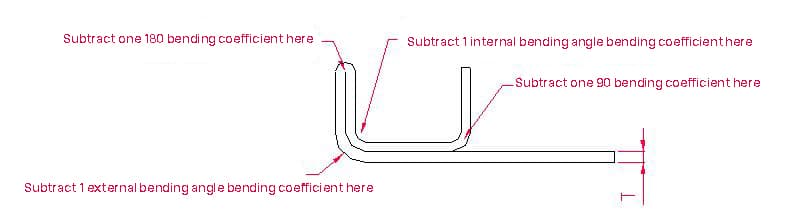
Doblar subsidio tabla para diferentes ángulos de flexión
| Espesor de la placa mm | 30 | 45° | 60° | 120° | 135 | 145° |
|---|---|---|---|---|---|---|
| 1.0 | 0.35 | 0.7 | 1.1 | 1.0 | 0.6 | 0.4 |
| 1.2 | 0.4 | 0.8 | 1.2 | 1.0 | 0.6 | 0.4 |
| 1.5 | 0.5 | 1.0 | 1.6 | 1.4 | 0.9 | 0.6 |
| 2.0 | 0.6 | 1.2 | 2.0 | 1.7 | 1.1 | 0.7 |
| 2.5 | 0.8 | 1.6 | 2.6 | 2.2 | 1.4 | 0.85 |
| 3.0 | 1.0 | 2.2 | 3.4 | 2.8 | 2.0 | 1.2 |
| 4.0 | 3.7 | 2.4 | 1.4 |
1. Ejemplo de diseño de desdoblamiento del proceso de piezas
1.1 Ejemplo de plano desplegable del proceso de curvado de cantos en ángulo recto.
1.1.1 Ejemplo de dibujo de despliegue de un pliegue y fórmula de cálculo
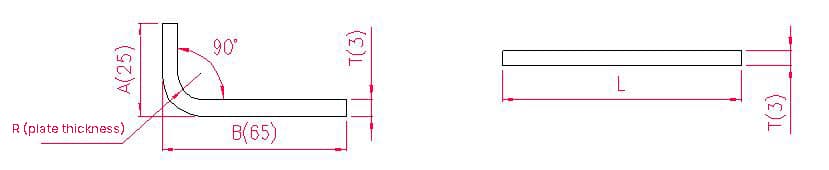
- A, B - longitud de la curva de la pieza
- P' - sobremedida de flexión por codo (sobremedida de flexión: restar una sobremedida por cada codo)
- R - radio de curvatura (normalmente igual al grosor de la placa)
- T - espesor del material
Longitud de despliegue: L = A + B - P', es decir, L = 25 + 65 - 5,5 = 84,5
Según la tabla 1: Para un espesor de chapa de 3 mm, debe utilizarse la matriz inferior V25, con una tolerancia de flexión de 5,5.
Nota: De acuerdo con la Tabla 1, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.1.2 Ejemplo de plano de despliegue de dos curvas y fórmula de cálculo
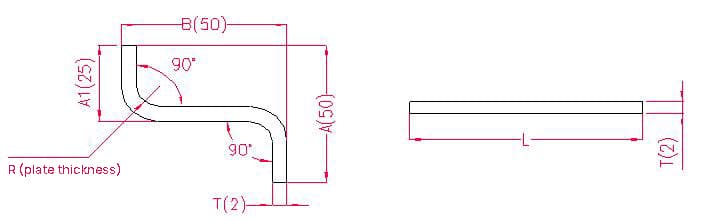
- A(A1), B - longitud de la curva de la pieza
- P - sobremedida de flexión por pliegue (sobremedida de flexión: restar una sobremedida por cada pliegue)
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Longitud de despliegue: L = A + T + B - 2xP', es decir, L = 50 + 2 + 50 - 2×3,4 = 95,6
Según la tabla 1: Para un espesor de chapa de 2 mm, debe utilizarse la matriz inferior V12, con una tolerancia de flexión de 3,4.
Nota: De acuerdo con la Tabla 1, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.1.3. Ejemplo de dibujo de despliegue de tres curvas y fórmula de cálculo
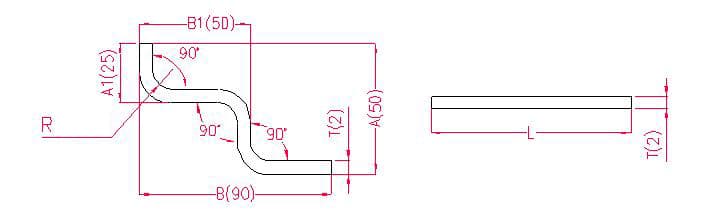
- A(A1), B(B1) - longitud de la curva de la pieza
- P - sobremedida de flexión por pliegue (sobremedida de flexión: restar una sobremedida por cada pliegue)
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Longitud de despliegue: L = A + T + B + T - 3xP', es decir, L = 50 + 2 + 90 + 2 - 3×3,4 = 133,8
Según la tabla 1: Para un espesor de chapa de 2 mm, debe utilizarse la matriz inferior V12, con una tolerancia de flexión de 3,4.
Nota: De acuerdo con la Tabla 1, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.1.4. Ejemplo de dibujo de despliegue de cuatro curvas y fórmula de cálculo
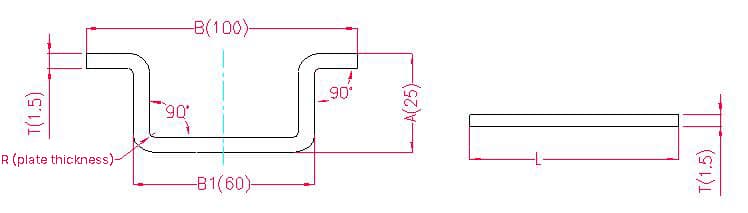
- A, B(B1) - longitud de la curva de la pieza
- P - sobremedida de flexión por pliegue (sobremedida de flexión: restar una sobremedida por cada pliegue)
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Longitud de despliegue: L = A + A + B + T + T - 4xP', es decir, L = 25 + 25 + 100 + 1,5 + 1,5 - 4×2,8 = 141,8
Según la tabla 1: Para un espesor de chapa de 1,5 mm, debe utilizarse la matriz inferior V12, con una tolerancia de flexión de 2,8.
Nota: De acuerdo con la Tabla 1, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.1.5. Ejemplo de plano de desdoblamiento de seis curvas y fórmula de cálculo
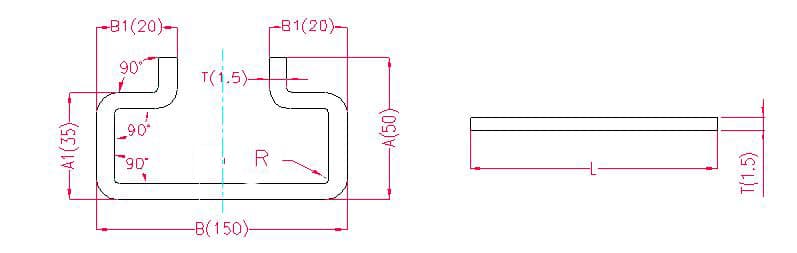
- A(A1), B(B1) - longitud de la curva de la pieza
- P' - sobremedida de flexión por codo (sobremedida de flexión: restar una sobremedida por cada codo)
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Longitud de despliegue: L = A + T + A + T + B + B1 + B1 - 6xP', es decir, L = 50 + 1,5 + 50 + 1,5 + 150 + 20 + 20 - 6×2,8 = 276,2
Según la tabla 1: Para un espesor de chapa de 1,5 mm, debe utilizarse la matriz inferior V12, con una tolerancia de flexión de 2,8.
Nota: De acuerdo con la Tabla 1, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.2.1. Ejemplos y fórmulas de cálculo para el despliegue por flexión de 180°.
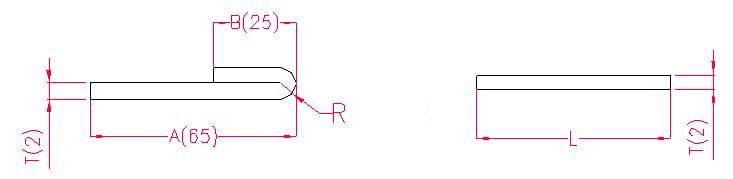
- A, B - longitud de la curva de la pieza
- P - Tolerancia de flexión del radio de aplanamiento
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Longitud de desdoblamiento: L = A + B - P', es decir, L = 25 + 65 - 1 = 89
Según la tabla 2: Para un espesor de chapa de 2 mm, debe utilizarse la matriz inferior V12, con un margen de flexión de la mitad del espesor de la chapa.
Nota: De acuerdo con la Tabla 2, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.2.2. Ejemplos y fórmulas de cálculo para el plegado-desplegado de doble capa.
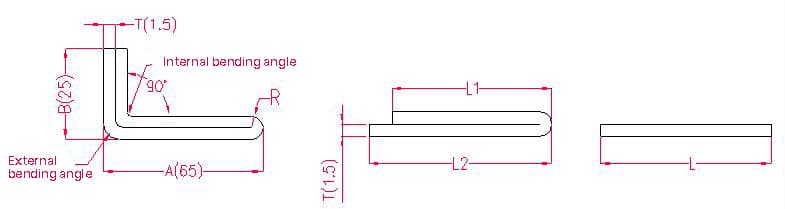
- A, B - longitud de la curva de la pieza
- P1 - margen de flexión para esquinas interiores
- P2 - margen de flexión para esquinas exteriores
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Longitud de despliegue: L1 = (A-1,5) + (B-1,5) - P1, es decir, L1 = (65-1,5) + (25-1,5) - 3,2 = 83,8
L2 = A + B - P2, es decir, L2 = 65 + 25 - 4,1 = 85,9
L = L1 + L2 - T/2, es decir, L = 83,8 + 85,9 - 0,75 = 168,95
Según la tabla 2: Para un espesor de chapa de 1,5 mm, debe utilizarse la matriz inferior V12, con un margen de flexión de 3,2 para las esquinas interiores, 4,1 para las esquinas exteriores y 0,75 para un ángulo de 180°.
Nota: De acuerdo con la Tabla 2, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.2.3. Ejemplos y fórmulas de cálculo para el plegado-desplegado de doble capa.
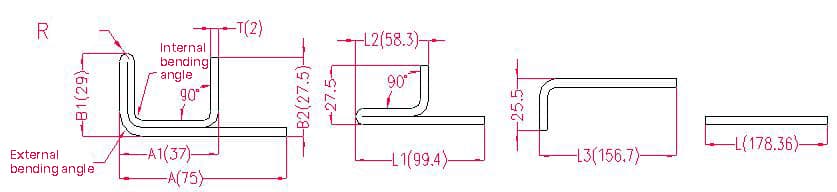
- A(A1), B1B2- longitud de la curva de la pieza
- P1 - margen de flexión para el ángulo interno
- P2 - margen de flexión para el ángulo exterior
- P3 - margen de flexión de 90
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
- P4 - margen de flexión de 180
Longitud de despliegue: L1 = A + B1 - P2, es decir, L1 = 75 + 29 - 4,6 = 99,4
L2 = (A1 - T) + (B1 - T) - P1, es decir, L2 = (37 - 2) + (29 - 2) - 3,7 = 58,7
L3 = L1 + L2 - P3, es decir, L3 = 99,4 + 58,3 - 1 = 156,7
L = 25,5 + L3 - P1, es decir, L = 25,5 + 156,7 - 3,84 = 178,36
Según la tabla 2: Para un espesor de chapa de 1,5 mm, debe utilizarse la matriz inferior V12, con una tolerancia de flexión en ángulo interior de 3,2, una tolerancia de flexión en ángulo exterior de 4,1 y una tolerancia de flexión a 180° de 0,75.
Nota: De acuerdo con la Tabla 2, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.2.4. Ejemplos y Fórmulas de Cálculo para el Desdoblamiento por Flexión de Doble Capa.
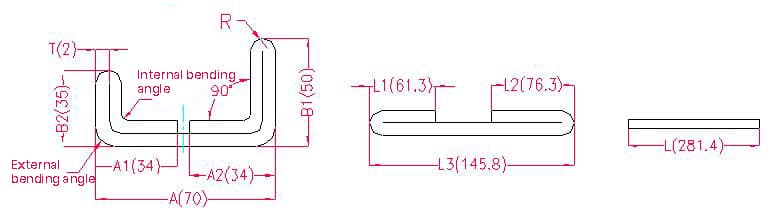
- A, A1, A2, B1, B2, L, L1, L2, L3 - longitud de la curva de la pieza
- P1 - margen de flexión para el ángulo interno
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
- P2 - margen de flexión para el ángulo exterior
Longitud de despliegue: L1 = (A1-T) + (B2-T) - P1, es decir, L1 = (35-2) + (34-2) - 3,7 = 61,3
L2 = (B1-T) + (A2-T) - P1, es decir, L2 = (50-2) + (34-2) - 3,7 = 76,3
L3 = A + B1 + B2 - 2 x P2, es decir, L3 = 70 + 35 + 50 - 2 x 4,6 = 145,8
L = L1 + L2 + L3 - 2 x P3, es decir, L = 61,3 + 75,3 + 145,8 - 2 x 1 = 281,4
Según la tabla 2: Para un espesor de chapa de 2 mm, debe utilizarse la matriz inferior V12, con una tolerancia de flexión en ángulo interior de 3,7, una tolerancia de flexión en ángulo exterior de 4,6 y una tolerancia de flexión en 180° de 1.
Nota: De acuerdo con la Tabla 2, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.3.1. Ejemplos y fórmulas de cálculo para el plegado en ángulo especial Desplegado.
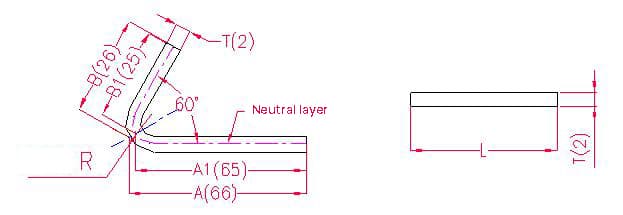
- A(A1), B(B1) - longitud de la curva de la pieza
- P - margen de flexión para un ángulo de flexión (varía con el ángulo)
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Longitud de desdoblamiento: L = (A-T) + (B-T) - P' = A1 + B1 - P', es decir, L = (66-1) + (26-1) - 2 = 65+25-2 = 88
Según la tabla 3: Para un espesor de chapa de 2 mm, debe utilizarse la matriz inferior V12, y la tolerancia de flexión para un ángulo de 60° es de 2.
Nota: Según la tabla 3, la capa neutra debe utilizarse como longitud y anchura de flexión.
1.3.2. Ejemplos y fórmulas de cálculo para el desdoblamiento por prensado escalonado.
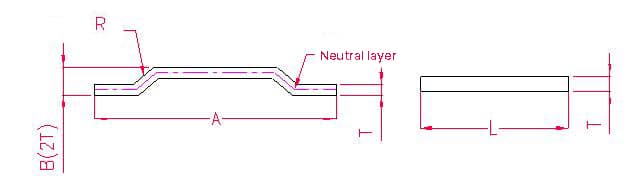
- A, B - longitud de la curva de la pieza
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Longitud de desdoblamiento: L = A + 1
Nota: Cuando el escalón sea igual a dos grosores de placa, añada 0,5 para cada escalón, y añada 1 para dos escalones.
1.3.3. Ejemplos y fórmulas de cálculo para el desdoblamiento de ángulos especiales.
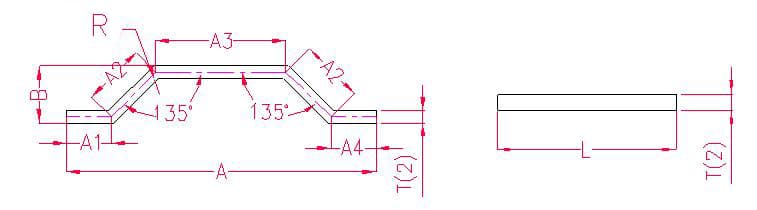
- A(A1A2A3A4), B - longitud de la curva de la pieza
- P - margen de flexión para un ángulo de 135
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Longitud de desdoblamiento: L = A1 + A2 + A3 + A2 + A4 - P - P
Nota: Para doblar con escalones, basta con restar dos márgenes.
Según la tabla 3: Para un espesor de chapa de 2 mm, debe utilizarse la matriz inferior V12, y la tolerancia de flexión para un ángulo de 135° es de 1,1.
1.3.4. Ejemplos y fórmulas de cálculo para el desdoblamiento de ángulos especiales.
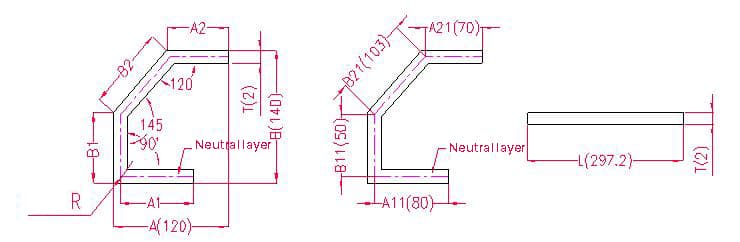
- A(A1A2), B(B1B2) - longitud de la curva de la pieza
- P1 - margen de flexión para un ángulo de 120
- P2 - margen de flexión para un ángulo de 145
- P3 - margen de flexión de 90
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
Nota: Cuando la dimensión está marcada en el contorno, es necesario convertirla al tamaño de la capa neutra al calcular la longitud de despliegue.
Longitud de despliegue: L = A11 + B11 + B21 + A21 - P1 - P2 - P3, es decir, L = 80 + 50 + 103 + 70 - 1,7 - 0,7 - 3,4 = 297,2
Según la tabla 3: Para un espesor de chapa de 2 mm, debe utilizarse la matriz inferior V12, con una tolerancia de flexión de 1,7 para un ángulo de 120°, de 0,7 para un ángulo de 145° y de 3,4 para un ángulo de 90°.
Nota: De acuerdo con la Tabla 3, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.4.1. Ejemplos y fórmulas de cálculo para el desplegado de pestañas ordinario.
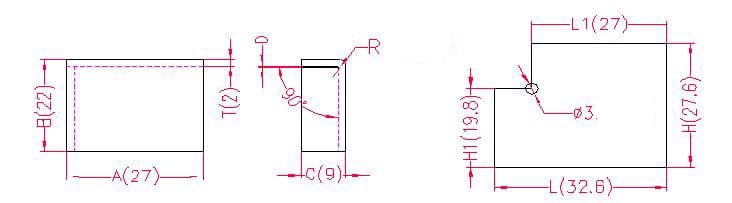
- A, B, C - longitud, anchura y altura de la curva de la pieza
- P - margen de flexión
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- H(H1), L(L1) - longitud de despliegue de cada lado
- T - espesor del material
- D - separación del proceso de flexión (normalmente entre 0 y 0,5)
Longitud de desdoblamiento: L1 = A, es decir, L1 = 27
L = A + C - P, es decir, L = 27 + 9 - 3,4 = 32,6
H1 = B - T - D, es decir, H1 = 22 - 2 - 0,2 = 19,8 (Nota: D se toma como 0,2)
H = B + C - P, es decir, H = 22 + 9 - 3,4 = 27,6
Según la tabla 1: Para un espesor de chapa de 2 mm, debe utilizarse la matriz inferior V12, con una tolerancia de flexión de 3,4.
Nota: De acuerdo con la Tabla 1, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.4.2. Ejemplos y Fórmulas de Cálculo para el Plegado Ordinario de Puertas.
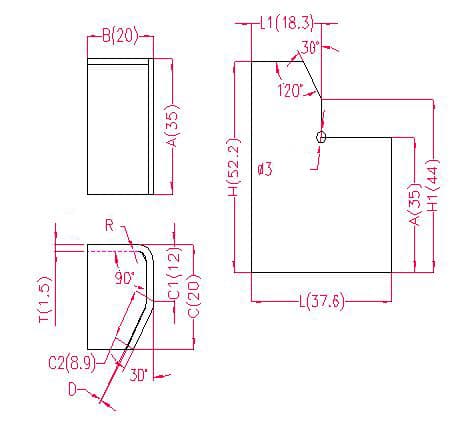
- A, B, C - longitud, anchura y altura de la curva de la pieza
- L(L1), H(H1) - longitud de despliegue de cada lado
- P - margen de flexión para un ángulo de 90
- P1 - margen de flexión para un ángulo de 30
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
- D - separación del proceso de flexión (normalmente entre 0 y 0,5)
Longitud de despliegue: L1 = B - T - D, es decir, L1 = 20 - 1,5 - 0,2 = 18,3
L = B + C1 + C2 - P - P1, es decir, L = 20 + 12 + 8,9 - 2,8 - 0,5 = 37,6
H1 = C1 + A - P - D, es decir, H1 = 12 + 35 - 2,8 - 0,2 = 44 (Nota: D se toma como 0,2)
H = A + C - P, es decir, H = 35 + 20 - 2,8 = 52,2
Según la tabla 1: Para un espesor de chapa de 1,5 mm, debe utilizarse la matriz inferior V12, con una tolerancia de flexión de 2,8 para un ángulo de 90° y de 0,5 para un ángulo de 30°.
Nota: De acuerdo con la Tabla 1, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.
1.4.3. Ejemplos y fórmulas de cálculo para plegado y desplegado de pestañas ordinarias.
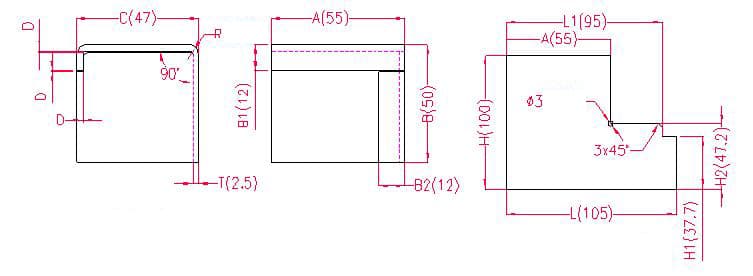
- A, B, C - longitud, anchura y altura de la curva de la pieza
- P - margen de flexión
- R - radio de curvatura (normalmente igual al grosor de la chapa)
- T - espesor del material
- D - separación del proceso de flexión (normalmente entre 0 y 0,5)
Longitud de desdoblamiento: H1 = B - B1 - D, es decir, H1 = 50 - 12 - 0,3 = 37,7 (Nota: D se toma como 0,2)
H2 = B - T - D, es decir, H2 = 50 - 2,5 - 0,3 = 47,2
H = B + C + B1 - 2xP, es decir, H = 50 + 47 + 12 - 2×4,5 = 100
L1 = A + C - T - D - P, es decir, L1 = 55 + 47 - 2,5 - 0,3 - 4,5 = 94,7
L = A + C+ B2 - 2xP, es decir, L = 55 + 47 + 12 - 2×4,5 = 105
Según la tabla 1: Para un espesor de chapa de 2,5 mm, debe utilizarse la matriz inferior V16, con una tolerancia de flexión de 4,5.
Nota: De acuerdo con la Tabla 1, las diferentes matrices inferiores tienen diferentes tolerancias de flexión, y los diferentes espesores de chapa tienen diferentes tolerancias de flexión.

