1. Biegung Rückfederung
Wie jede Form der plastischen Verformung geht auch das Biegen von Rohren mit einer elastischen Verformung einher. Wenn die Last entfernt wird, verkürzen sich die Fasern auf der Außenseite der neutralen Biegeschicht aufgrund der elastischen Erholung, und die Fasern auf der Innenseite verlängern sich, wodurch sich die Biegegeschwindigkeit und der Biegewinkel ändern. Dieses Phänomen wird als Rückfederung bezeichnet. Es gibt zwei Formen der Rückfederung, wie in Abbildung 4-25 dargestellt.
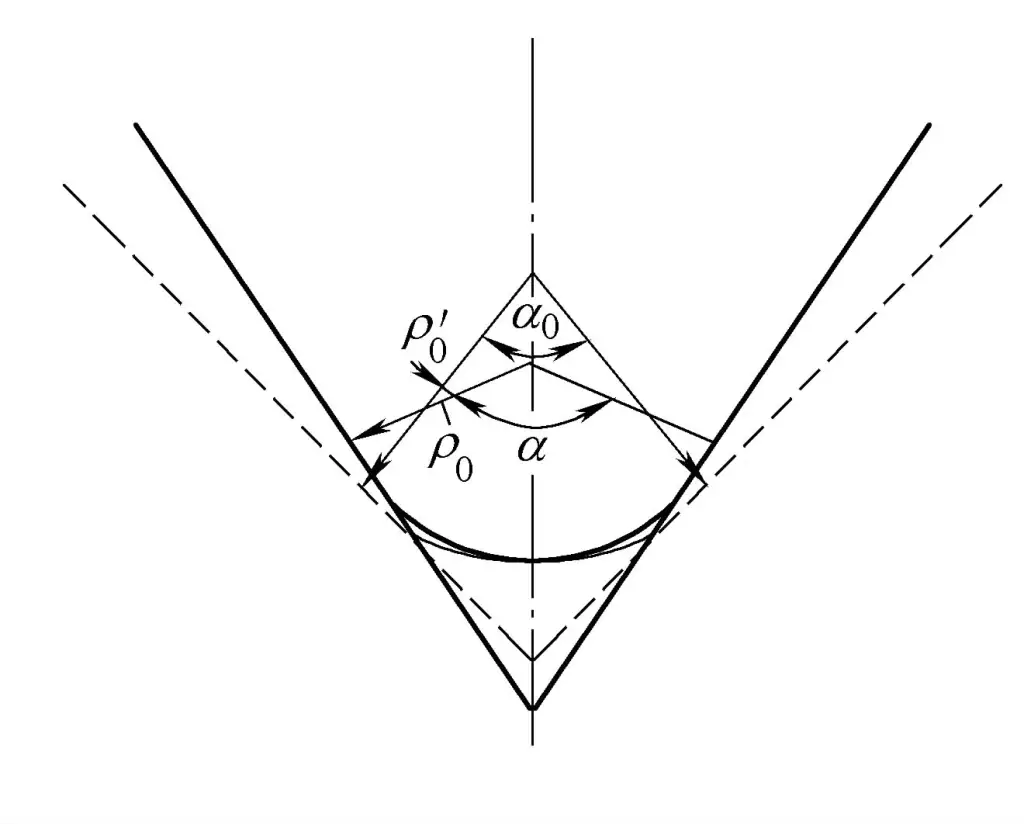
1) Die Krümmung nimmt ab.
Die Krümmung verringert sich von 1/ρ0 vor dem Entladen auf 1/ρ'0 nach dem Entladen.
2) Der Biegewinkel nimmt ab.
Der Biegewinkel sinkt von α vor der Entlastung auf α 0 nach der Entlastung. Das Ausmaß der Rückfederung kann durch die Änderung der Krümmung ΔK oder die Änderung des Biegewinkels Δα (auch Rückfederungswinkel genannt) berechnet werden.
Δα = α - α 0
(1) Faktoren, die die Biegerückfederung beeinflussen
Beim Biegen gibt es viele Faktoren, die das Ausmaß der Rückfederung beeinflussen, die wichtigsten sind folgende:
1) Die mechanischen Eigenschaften des Rohlings.
Je kleiner der Wert von σs /E, d.h. je kleiner σs und je größer der Wert von E ist, desto kleiner ist der Rückfederungswert Δα.
2) Der Grad der Verformung r/t.
Unter den gleichen Bedingungen, je kleiner das r/t, desto größer ist der Grad der Biegeverformung, der Anteil der elastischen Verformung an der Gesamtverformung nimmt ab, so dass die Rückfederung der Biegung abnimmt.
3) Zentraler Biegewinkel α.
Je größer der zentrale Biegewinkel α ist, desto größer ist die Länge der Verformungszone. Unter den gleichen Verformungsbedingungen nimmt der Verformungsbetrag pro Längeneinheit ab. Je größer der Biegewinkel α ist, desto größer ist daher der Anteil der elastischen Verformung an der Gesamtverformung und desto größer ist der Rückfederungswert Δa.
4) Spielraum der Matrize Z.
Größere Schnittspalt, größere Rückfederung.
5) Biegeverfahren.
Die Rückfederung ist beim Zugbiegen gering und beim Druckbiegen am kleinsten.
6) Form des Werkstücks und Zustand der Materialstruktur.
Komplexe Formen, mehrfache gegenseitige Beanspruchung führen zu geringer Rückfederung, große Rückfederung nach Kaltverfestigung.
7) Struktur der Form und Größe der Presskraft.
Die Kantenpresskraft ist groß, was zu einem kleinen Rückprallbetrag nach dem Biegen des Werkstücks führt.
(2) Bestimmung des Rückprallwertes
Die Bestimmung des Rückprallwerts des Werkstücks dient dazu, entsprechende Maßnahmen zur Überwindung des Rückpralls zu ergreifen, damit das gebogene Werkstück die Genauigkeitsanforderungen des Entwurfsmusters erfüllen kann. Zu den Methoden zur Bestimmung des Rückprallwertes gehören die Lookup-Diagramm-Methode, die Lookup-Table-Methode und die Berechnungsmethode.
In Wirklichkeit BiegeumformungAndererseits ist es schwierig, die neutrale Schicht während des Biegeprozesses von Profilen genau zu bestimmen, was die Berechnung des Rückpralls erschwert. Die Berechnung des Rückpralls beim Biegen von Profilen ist viel komplexer als beim Biegen von Blechen, so dass die Methoden zur Berechnung des Rückpralls von Rohrbiegen sind allesamt Näherungswerte und weichen stark von der tatsächlichen Situation ab.
Gegenwärtig wird sowohl im Inland als auch auf internationaler Ebene noch über den Rebound geforscht. Da der Rückprall von vielen Faktoren abhängt und recht komplex ist, gibt es derzeit keine genaue Berechnungsformel. Daher wird die Kontrolle des Rückprallwerts im Allgemeinen mit Hilfe von Formen unterschiedlicher Struktur korrigiert, hauptsächlich während der Formprüfung.
(3) Methoden zur Verringerung und Verhinderung des Rückpralls
Die Methoden zur Verringerung und Verhinderung des Rückpralls lassen sich aus prinzipieller Sicht in zwei Hauptkategorien einteilen. Die erste Kategorie von Methoden gewährleistet die Form des Teils nach dem Rückprall, indem sie die Verformung erhöht. Die wichtigsten Maßnahmen dieser Kategorie bestehen darin, die Form der Form zu korrigieren, die Biegekrümmung des Teils zu verringern oder den Biegewinkel zu vergrößern, so dass das Teil nach dem Rückprall die Konstruktionsanforderungen erfüllt.
Eine weitere Kategorie von Methoden besteht darin, den Rückprall durch Veränderung der Spannungsverteilung des verformten Biegeteils zu verringern. Die am häufigsten angewandte Maßnahme in dieser Kategorie ist die Anwendung einer tangentialen Zugspannung, wodurch die Spannungsverteilung im Querschnitt des gebogenen Teils gleichmäßig wird, wodurch die Ungleichmäßigkeit der elastischen Erholung während der Entlastung verringert und der Rückprall reduziert wird.
Der Rückprall bei der Biegeumformung ist einer der Hauptfaktoren, die die Maßgenauigkeit und die Produktionseffizienz von Teilen beeinflussen. Da die Vorhersage des Rückpralls eng mit dem gesamten Umformprozess zusammenhängt, ist das Rückprallproblem recht komplex und ein heißer und schwieriger Punkt in der Forschung von Profilbiegen bilden. Viele Wissenschaftler im In- und Ausland haben eingehende Untersuchungen und Diskussionen durchgeführt.
Derzeit gibt es mehrere Methoden, um das Problem des Rückpralls beim Rohrbiegen zu lösen:
1) Führen Sie die Tabelle der Rückpralldaten auf der Grundlage von Erfahrungswerten auf.
So haben zum Beispiel mehrere inländische Werften CNC Rohrbiegemaschinen der amerikanischen Firma WALLACE COAST, die zur Rückprallkompensation einen Erfahrungsdatensatz im Steuerungssystem verwenden. Aufgrund des großen Fehlers dieser Methode ist die Biegegenauigkeit der CNC-Rohrbiegemaschine jedoch nicht ideal.
2) Anwendung theoretischer Berechnungsmethoden.
Da die Kraftsituation beim Biegen von Rohren sehr komplex ist, bei den Berechnungen Annahmen und Vereinfachungen getroffen werden müssen und die Materialeigenschaften und die tatsächlichen Arbeitsbedingungen schwer vorhersehbar sind, wurde bisher kein erfolgreicher Präzedenzfall für die Anwendung von theoretischen Berechnungsformeln zur Rückfederung in der Praxis gefunden, und es besteht weiterer Diskussionsbedarf.
3) Im Flugzeug- und Automobilbau wird seit vielen Jahren die von der amerikanischen Firma EATON LEONARD vertretene Methode angewendet.
Bei dieser Methode wird davon ausgegangen, dass es zwar viele Faktoren gibt, die den Rückprall beim Biegen von Rohren beeinflussen, aber sobald die Werkzeugmaschine eingestellt ist, die Prozessparameter (BiegeradiusZu diesem Zeitpunkt wird die Beziehung zwischen dem Biegewinkel und dem Umformwinkel nach dem Rückprall unter den Bedingungen des Biegens einer Charge von Materialrohren gemessen, so dass der Drehwinkel des Rohrbiegemaschinenarms und der Umformwinkel des Rohrs als eine lineare Beziehung betrachtet werden können.
Die Methode besteht darin, die Rohre bei 125° und 22° auf der Rohrbiegemaschine zu biegen, und nachdem die Rohre gebogen sind, sie auf die CNC-Rohrformmessmaschine zu legen, um ihre tatsächlichen Formungswinkel von 120° und 20° zu messen, wobei eine Geradengleichung durch zwei Punkte aufgestellt wird, um die Beziehung zwischen dem Drehwinkel des Rohrbiegemaschinenarms und dem erforderlichen Formungswinkel des Rohrs zu erhalten. Diese Methode hat eine gute Wirkung.
Um das Problem des Rückpralls beim Biegen von Rohren zu lösen, wurden die folgenden Arbeiten durchgeführt:
1) Es wurde eine große Anzahl von Rückprallexperimenten durchgeführt.
Durch die Durchführung von kernlosen und kernhaltigen Rohrbiegeversuchen mit verschiedenen Spezifikationen auf mehreren Rohrbiegemaschinen und die Durchführung von Regressionsanalyseberechnungen mit den gemessenen Daten ist bekannt, dass der Biegewinkel α und der Umformwinkel α 0 linear ändern, was mit der theoretischen Berechnung der linearen Änderung übereinstimmt. Anders jedoch, diese Linie geht nicht durch den Ursprung, es gibt einen Streckenabschnitt C1 wie in Abbildung 4-26 dargestellt.
α = K1 α0 + C1
In der Formel wird K1 ist die Steigung einer Geraden;
C1 ist der Schnittpunkt einer Geraden.
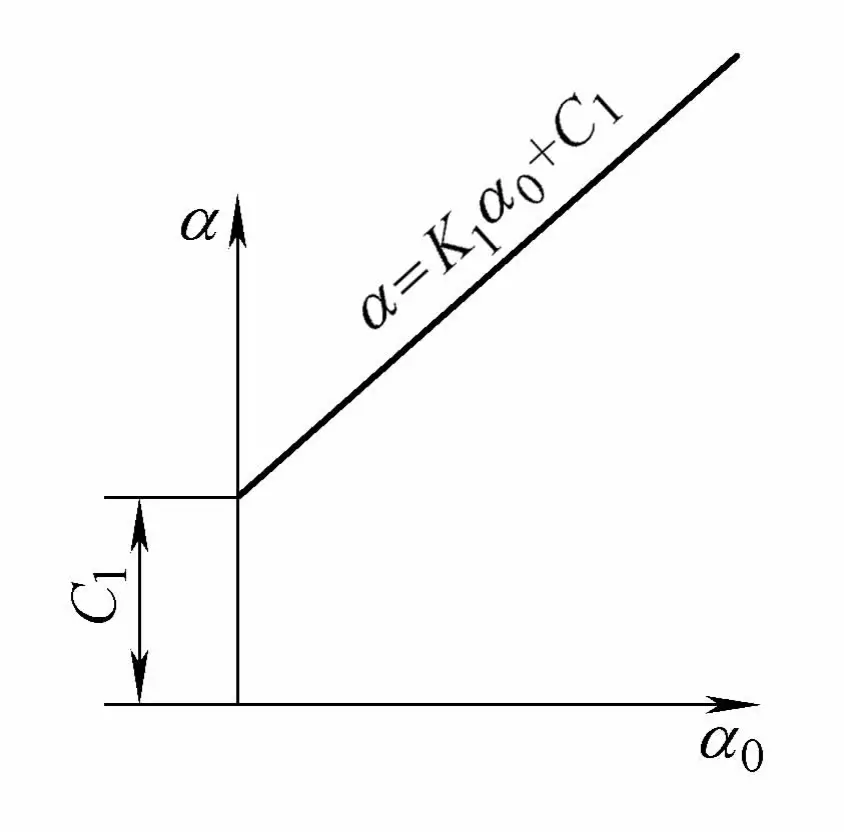
Aus der obigen Formel lässt sich die folgende Schlussfolgerung ziehen: Für Rohre, die aus der gleichen Materialcharge gebogen werden, gilt innerhalb des Bereichs der technischen Biegewinkel die Beziehung zwischen dem Biegewinkel α und dem Umformwinkel α 0 ist immer eine gerade Linie, die nicht durch den Ursprung verläuft.
2) Theoretische Analyse der Rückfederung von Rohrbiegeversuchen.
Um die Korrektheit der Schlussfolgerungen aus dem Rückfederungsversuch zu analysieren, wurde eine Kraftanalyse für die Arbeitsbedingungen der Rohrbiegemaschine durchgeführt, und nach einigen Annahmen und Vereinfachungen wurden zahlreiche Berechnungen vorgenommen.
Die Berechnungsergebnisse zeigen, dass innerhalb eines kleineren Bereichs von Biegewinkeln die Beziehung zwischen dem Biegewinkel α und dem Umformwinkel α 0 gekrümmt ist, und nachdem der Biegewinkel größer als 1 ist, ist die Beziehung zwischen dem Biegewinkel α und dem Umformwinkel α 0 ist linear und folgt demselben Trend wie die während des Versuchs beobachtete lineare Beziehung, was die Richtigkeit der Schlussfolgerungen aus dem Rückfederungsversuch beweist.
Es ist zu beachten, dass zwischen den beiden Werten ein erheblicher Unterschied besteht, der auf die Annahmen und Vereinfachungen in den theoretischen Berechnungen und die Tatsache zurückzuführen ist, dass die tatsächlichen Rohrbiegebedingungen viel komplexer sind als die berechneten Situationen.
Daher geht die oben genannte Arbeit tiefer als die von der Firma EATON LEONARD vertretenen Forschungsergebnisse, die "die Beziehung zwischen dem Drehwinkel des Rohrbiegemaschinenarms und dem Biegewinkel des Rohrs als linear" betrachtet.
Zusammenfassend lässt sich sagen, dass das Problem der Rückfederung beim Biegen von Rohren derzeit am besten wie folgt gelöst werden kann: Beim Biegen einer Charge von Rohren können zwei verschiedene Biegeversuche (z. B. 30° und 90°) auf der betreffenden Rohrbiegemaschine durchgeführt werden. Während des Versuchs werden die beiden tatsächlichen Drehwinkel des Armes der Rohrbiegemaschine α1 , α2 und messen Sie die beiden Formungswinkel des Rohrs α01 , α02 . Berechnen Sie dann die Koeffizienten nach der folgenden Formel.
K1 = (α 2 - α 1 ) / (α 02 - α 01 )
C1 = α 1 - α 1 (α 2 - α 1 ) / (α 02 - α 01 )
Setzt man die beiden obigen Formeln in die Formel für α im Rückprallversuch ein, so erhält man die lineare Gleichung, die die Rückprallregel für diese Charge von Rohrmaterial darstellt.
2. Biegedehnung
Nach dem Biegen auf einer Biegemaschine vergrößert sich die axiale Länge eines Rohrs einer bestimmten Länge, ein Phänomen, das als Biegedehnung bekannt ist. Die Zunahme der axialen Länge wird als Dehnung des Rohrs bezeichnet. Die Biegedehnung beeinträchtigt die Maßhaltigkeit der Teile. In der Vergangenheit wurden unter anderem folgende Methoden zur Lösung dieses Problems eingesetzt:
1) Für den Einsatz in der Produktion wurde eine auf Erfahrung basierende Dehnungsdatentabelle erstellt, deren Anwendung jedoch einen großen Fehler aufweist.
2) Berechnungsmethoden im Zusammenhang mit der Theorie der Biegedehnung von Rohren. Wie beim Rückprall gibt es derzeit keine theoretische Berechnungsformel, die in der Praxis erfolgreich angewandt wurde, was noch weiter diskutiert werden muss.
3) Im Flugzeug- und Automobilbau wird seit vielen Jahren eine von der Firma EATON LEONARD vertretene Methode angewandt, bei der bei der Messung des Rückpralls mit einem CNC-Rohrprofilierer die so genannte Bogenkonstante anhand einer Formel berechnet wird, die die verwendete Materiallänge bei einem Biegewinkel von 100° darstellt, wobei auch berücksichtigt wird, dass die Dehnung des Rohrs direkt proportional zum Umformwinkel ist.
Um das Problem der Dehnung beim Biegen von Rohren zu lösen, wurde die folgende Arbeit durchgeführt:
1) Es wurde eine große Anzahl von Dehnungsversuchen durchgeführt.
Durch die Durchführung verschiedener Spezifikationen von kernlosen und kernhaltigen Biegeexperimenten auf mehreren Biegemaschinen in fünf Werften und die Durchführung von Regressionsanalyseberechnungen zu den von jeder Materialcharge erhaltenen Daten ist bekannt, dass die Dehnung △L eine lineare Beziehung mit dem Umformwinkel α' hat, die nicht durch den Ursprung verläuft. Das heißt:
ΔL = K 2 α'+C 2
In der Formel,
- K 2 - die Steigung der Linie;
- C 2 - gerade Linie.
Die Regressionsanalyse der gemessenen Daten zeigt, dass der Korrelationskoeffizient γ zwischen 0,97 und 0,99 liegt, was eine klare lineare Beziehung zeigt. Daher kann die folgende Schlussfolgerung gezogen werden: Für Rohre derselben Materialcharge besteht innerhalb des Bereichs der technischen Biegewinkel eine lineare Beziehung zwischen der Dehnung ΔL und dem Umformwinkel α', die nicht durch den Ursprung verläuft.
2) Die Regressionsüberprüfung wurde auch anhand der Tabellen mit Rückfederungsdaten von verbundenen Werften durchgeführt.
Aus empirischen Berechnungen ist bekannt, dass die Dehnung ΔL und der Umformwinkel α' ebenfalls eine lineare Beziehung aufweisen, wobei der Korrelationskoeffizient γ über 0,99 liegt, was auf eine hohe Linearität hindeutet, der Achsenabschnitt jedoch im Allgemeinen klein ist.
3) Theoretische Analyse des Experiments zur Rohrbiegedehnung.
Um die Richtigkeit der Schlussfolgerungen aus dem Dehnungsexperiment weiter zu belegen, wurde eine Kraftanalyse für die Rohrbiegebedingungen der Rohrbiegemaschine durchgeführt, und nachdem einige Annahmen und Vereinfachungen vorgenommen worden waren, wurde eine große Anzahl von Berechnungen durchgeführt. Die Berechnungsergebnisse zeigen, dass innerhalb eines kleinen Biegewinkelbereichs die Dehnung ΔL und der Umformwinkel α' eine gekrümmte Beziehung haben; wenn der Biegewinkel größer als 3° ist, haben die Dehnung ΔL und der Umformwinkel α' eine lineare Beziehung.
Der lineare Beziehungsteil der theoretischen Analyse und die Tendenz der linearen Beziehung während des Versuchs stimmen überein, was die Richtigkeit der Schlussfolgerungen des Rohrbiegedehnungsversuchs beweist. Es ist anzumerken, dass ein erheblicher Unterschied zwischen den beiden Werten besteht, der durch die Annahmen und Vereinfachungen der theoretischen Berechnungen und die tatsächlichen Rohrbiegebedingungen verursacht wird, die viel komplexer sind als die berechneten Situationen.
Die Schlussfolgerung der Studie, dass für Rohre der gleichen Materialcharge innerhalb des Bereichs der technischen Biegewinkel die Dehnung ΔL und der Umformwinkel α' eine lineare Beziehung aufweisen, die nicht durch den Ursprung verläuft, unterscheidet sich von der traditionell vertretenen Ansicht, dass die Dehnung direkt proportional zum Umformwinkel ist, wobei die erstere eher der tatsächlichen Situation beim Biegen von Rohren durch den Rohrbieger entspricht.
Zusammenfassend lässt sich sagen, dass das Problem der Biegedehnung von Rohrmaterial derzeit am besten wie folgt gelöst werden sollte: Beim Biegen einer Charge von Rohrmaterial können zwei Biegeversuche mit der gleichen Länge L, aber unterschiedlichen Biegungen (z. B. 30° und 90°) auf der gegebenen Rohrbiegemaschine durchgeführt werden. Nach dem Versuch werden die Rohre entnommen und die beiden tatsächlichen Biegewinkel α' 1 , α' 2 und die vergrößerten Längen der beiden tatsächlichen Rohrachsen L' 1 , L' 2 kann die Dehnung berechnet werden.
ΔL1 = (L1 '-L) ΔL2 = (L2 '-L)
Daraus lassen sich die Koeffizienten der linearen Gleichung für ΔL mit Hilfe der beiden folgenden Formeln berechnen.
K 2 = (ΔL 2 -ΔL 1 ) / (α' 2 -α' 1 )
C 2 = ΔL 1 -α' 1 (ΔL 2 -ΔL 1 ) / (α' 2 -α' 1 )
Setzt man die beiden obigen Gleichungen in die lineare Gleichung über ΔL ein, erhält man das Dehnungsgesetz für diese Rohrserie. Das intelligente Rohrbiegemessgerät kann dieses Dehnungsgesetz auf bequeme Weise ermitteln.
3. Behandlungsmethode für das Problem des Umformradius nach dem Rohrbiegen und der Rückfederung
Nachdem das Rohrmaterial gebogen ist und zurückfedert, wird sein Formradius R' größer als der Formradius R, was zu einer Änderung des Tangentenpunkts des Rohrs führt. Daher sollte die Biegemaschine beim Biegen von Rohren die dadurch verursachte Änderung des Ausgangs-Biegepunktes berücksichtigen. Die von der Firma EATON LEONARD angewandte Methode besteht darin, ein CNC-Rohrprofilmessgerät zu verwenden, um die relevanten Parameter der Rückfederung zu messen, dann den Formradius nach der Rückfederung mit einer Formel zu berechnen und diesen berechneten Radius zur Korrektur des Ausgangsbiegepunkts zu verwenden.
Bei der Verwendung dieser Formel für den Ausgangspunkt der Biegung wird festgestellt, dass beim Biegen von Rohren mit kleinen Spezifikationen (z. B. <3 mm) der Fehler zwar größer, aber immer noch brauchbar ist; beim Biegen von Rohren mit größeren Spezifikationen ist der Fehler besonders groß, und die Wirkung ist nicht gut. Dies ist auch auf die sehr komplexe Situation beim Biegen von Rohren und die Schwierigkeiten bei der Vorhersage der Materialeigenschaften und der tatsächlichen Arbeitsbedingungen zurückzuführen, so dass die theoretische Berechnungsformel für den Umformradius den tatsächlichen Anforderungen nicht gerecht wird.
Wenn der Anfangspunkt der Biegung nicht gut gehandhabt wird, ist es schwierig, die Genauigkeit der Biegeumformung zu gewährleisten, und es treten Schwierigkeiten bei der Durchführung des randlosen Biegeverfahrens auf. Um dieses Problem zu lösen, sollten moderne Messgeräte eingesetzt werden.
Anhand einer bestimmten Rohrbiegemaschine wird der Verformungsradius einer Charge von Rohrmaterialien nach dem Biegen und der Rückfederung gemessen, was als Grundlage für die Bestimmung des Anfangspunkts des Biegeprozesses dient. Mit dem intelligenten Rohrbiegemessgerät kann der Umformradius des Rohrmaterials nach dem Biegen und der Rückfederung bequem ermittelt werden, und das Prinzip der Messberechnung ist in der folgenden Berechnungsformel dargestellt.
4. Verfahren zur Messung von Rückfederung, Dehnung und Umformradius mit einem intelligenten Rohrbiegemessgerät
Das intelligente Rohrbiegemessgerät basiert hauptsächlich auf dem oben erwähnten Rohrbiegeprinzip und wurde speziell für den Einsatz mit CNC-Rohrbiegemaschinen entwickelt. Das Gerät besteht aus einer Messvorrichtung (einschließlich Messmechanismus, Winkelsensor) und einem Mikrocomputersystem (einschließlich Mikrocomputer, Schnittstellenkarte). Das Gerät verfügt über eine hohe Präzision, mit einem Winkel von 0,1° und einer Länge von 0,25 mm.
Der Messmechanismus des Geräts ist ein viergliedriger, planarer Mechanismus, wie in Abbildung 4-27 dargestellt, mit einem an den Knotenpunkten a, b und c installierten Winkelsensor, der den Winkel zwischen zwei benachbarten Stäben messen kann. Die Messköpfe an d und e sind planar, so dass die Stangen ad und be während der Messung senkrecht zum geraden Rohrabschnitt des dghe-Rohrs stehen können.
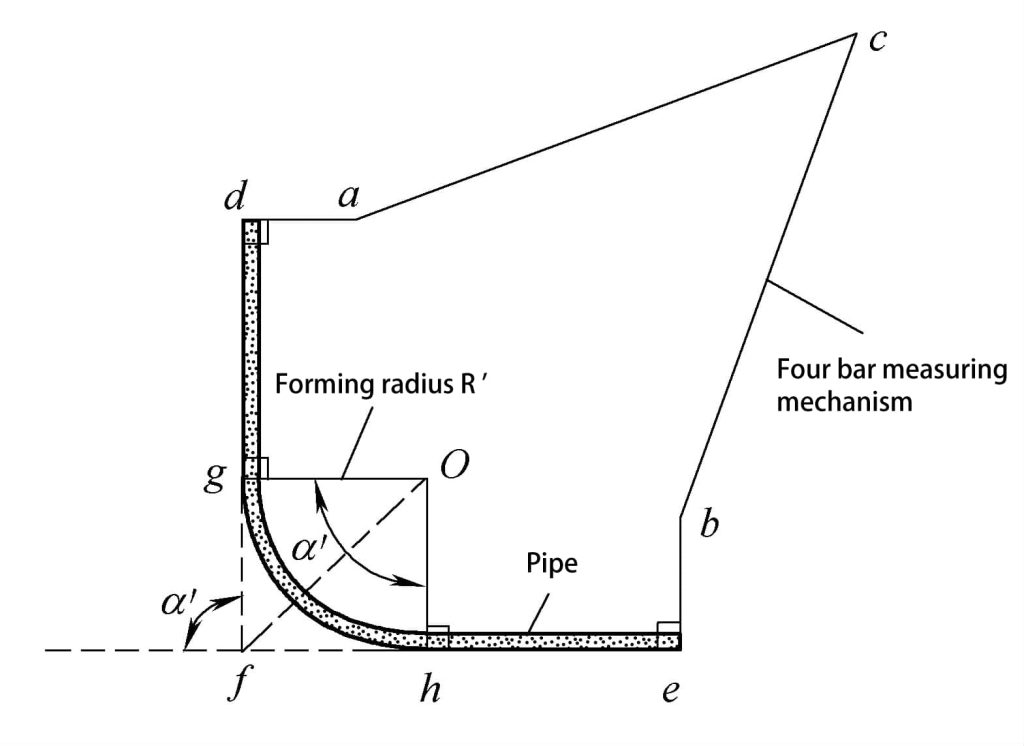
Die Längen der einzelnen Stangen des viergliedrigen, ebenen Mechanismus sind bekannt, so dass die relevanten geometrischen Parameter des dghe-Rohrs gemessen und berechnet werden können. Die Methode ist wie folgt:
1) Ausgehend von den bekannten Bedingungen des Mechanismus und dem vom Winkelsensor gemessenen Winkel kann der Umformwinkel α' des Rohrs berechnet werden.
2) Ausgehend von den bekannten Bedingungen des Mechanismus und dem vom Winkelsensor gemessenen Winkel können die Abstände df und fe der Schnittpunkte der geraden Rohrachse berechnet werden.
3) Wenn der Abstand dg des Anfangsbiegepunktes des Rohres Montage bekannt ist, kann der tatsächliche Umformradius R' weiter berechnet werden.
R'=O g = (df-dg) / tan(α'/2)
4) Die Länge L' der Rohrachse kann weiter berechnet werden.
L’=df+fe-2R’tan(α’/2) +πR’α’/180
Auf der Grundlage der obigen Grundsätze und Formeln ist es nur erforderlich, zwei Prüfstücke gleicher Länge L und mit Biegeansatzpunkten im Abstand d bzw. g auf der Rohrbiegemaschine unter vorgegebenen Winkeln (H 1 =30°, H=90°), dann entfernen Sie sie und messen Sie mit einem intelligenten Rohrbiegemessgerät, das die eigentliche Messung automatisch abschließen und das Rückprall-Variationsmuster, das Dehnungs-Variationsmuster und den geformten Radius nach dem Rückprall für verschiedene Metallmaterialien und Rohrmodelle ausdrucken kann.
Wenn die Rohrform des Werkstücks vorgegeben ist, kann das Gerät auch die Stanzdaten für das Biegen ohne Zugabe liefern und das Bearbeitungsprogramm für die CNC-Rohrbiegemaschine bereitstellen, einschließlich der Startpunktkorrektur und der Rückprallkompensation (das Gerät hat auch die Funktion, die Rohrform zu messen). Die vom Gerät gelieferten Daten verbessern nicht nur die Formgenauigkeit der CNC-Rohrbiegemaschine, sondern fördern auch den technologischen Fortschritt, indem sie die Arbeitsintensität verringern, Stahl einsparen und die Produktionseffizienz verbessern.
5. Biegeradius
Der Grad der Biegeverformung des Rohrmaterials hängt von den Werten des relativen Biegeradius R/D und der relativen Dicke t/D ab (R ist der Krümmungsradius der Querschnittsmittelschicht des Rohrmaterials, D ist der Außendurchmesser des Rohrmaterials, t ist die Wanddicke des Rohrmaterials). Je kleiner die Werte von R/D und t/D sind, desto größer ist der Grad der Biegeverformung, die äußere Wand der biegeneutralen Schicht wird zu dünn und führt sogar zum Bruch; die innerste Wand wird dicker und wird sogar instabil und faltig.
Gleichzeitig wird mit zunehmendem Verformungsgrad auch die Verformung des Querschnitts (Abflachung) immer stärker. Um die Qualität der Umformung des Rohrmaterials zu gewährleisten, ist es daher notwendig, den Verformungsgrad innerhalb eines zulässigen Bereichs zu steuern. Der zulässige Verformungsgrad für das Biegen des Rohrmaterials wird als Grenzwert für das Biegen bezeichnet. Die Biegegrenze des Rohrmaterials hängt nicht nur von den mechanischen Eigenschaften des Materials und der Biegemethode ab, sondern auch von den Anforderungen an die Verwendung der Rohrformstücke.
Für allgemeine Biegeteile ist die Bedingung für die Definition der Umformgrenze, dass die maximale Dehnungsdehnung ε max die an der am weitesten von der neutralen Schicht entfernten Stelle des äußeren Abschnitts des Biegeverformungsbereichs erzeugt wird, sollte den durch die Plastizität des Materials zulässigen Grenzwert nicht überschreiten.
Unter der Bedingung, dass die äußere Oberflächenschicht außerhalb des Verformungsbereichs des gebogenen Rohrformstücks nicht reißt, ist der Grenzbiegeradius r min die in die Innenseite des Teils gebogen werden kann, wird als Grenzwert für das Biegen von Rohrstücken verwendet. r min hängt von den mechanischen Eigenschaften des Materials, der Größe der Rohrformstückstruktur, dem Biegeverfahren und anderen Faktoren ab.
Der Mindestbiegeradius für verschiedene Biegeverfahren ist in Tabelle 4-6 angegeben.
Tabelle 4-6 Mindestbiegeradius für das Biegen von Rohren (Einheit: mm)
| Biegeverfahren | Minimaler Biegeradius (rmin) |
| Biegen mit der Presse | (3~5)D |
| Wrap Bending | (2~2.5)D |
| Walzenbiegen | 6D |
| Push-Bending | (2.5~3)D |
Anmerkung: D ist der Außendurchmesser des Rohrs.
Der Mindestbiegeradius für Stahl- und Aluminiumrohre ist in Tabelle 4-7 angegeben.
Tabelle 4-7 Mindestbiegeradius für Stahl- und Aluminiumrohre (Einheit: mm)
| Außendurchmesser des Rohrs | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
| Minimaler Biegeradius rmin | 8 | 12 | 16 | 20 | 28 | 32 | 40 | 45 | 50 | 56 |
| Außendurchmesser des Rohrs | 24 | 28 | 30 | 32 | 35 | 38 | 40 | 44 | 48 | 50 |
| Minimaler Biegeradius rmin | 68 | 84 | 90 | 96 | 105 | 114 | 120 | 132 | 144 | 150 |

