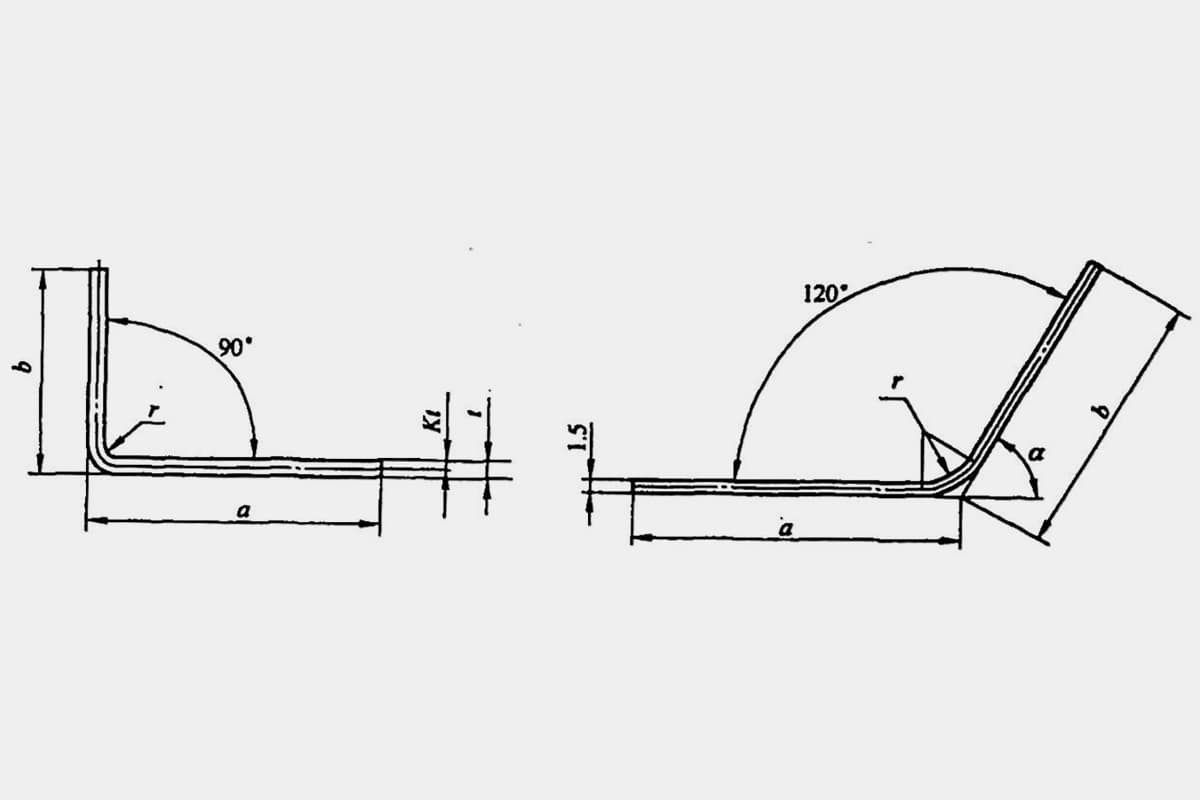
Bei Blechbiegeteilen ist die Berechnung der Rohteilgröße eine Voraussetzung für die Formulierung des Biegeverfahrensplans. Verschiedene Techniker können in ihren Prozessdokumenten unterschiedliche Biegezugabefaktoren wählen, und die Genauigkeit der Rohteilgröße wirkt sich direkt auf die Maßhaltigkeit und Produktqualität der Biegeteile aus.
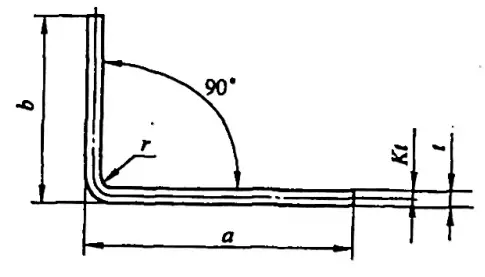
Manchmal können ungenaue Berechnungen sogar zu Abfallprodukten führen. Die entfaltete Länge L eines typischen einfachen Biegeteils (siehe Abbildung 5-1) ist L = a + b - y (wobei y der Biegeabzug ist, auch bekannt als Korrekturwert für das R-Teil).
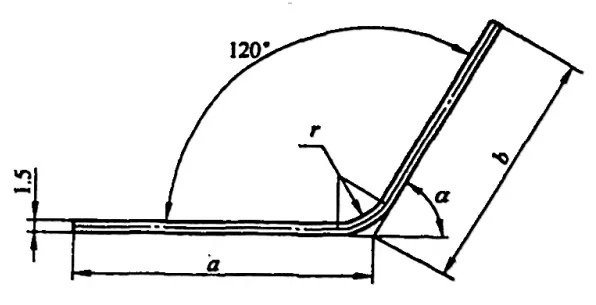
In verschiedenen Handbüchern und Materialien kann der Biegeabzug für φ=90° jedoch direkt ermittelt werden, während er bei Biegungen, die nicht 90° betragen, wie in Abbildung 5-2 gezeigt, von Technikern anhand eines Erfahrungsfaktors (K-Faktor) berechnet werden muss.
Weiterführende Lektüre: Die Kunst des Abfaltens von Blechen erklärt
1. Prinzip der Berechnung des Abwicklungsmaßes von Blechbiegungen
Die ungefaltete Abmessung einer gebogenen Platine wird nach dem Prinzip bestimmt, dass die Länge der neutralen Schicht vor und nach dem Biegen unverändert bleibt. Wenn das Blech gebogen wird, werden die Fasern der äußeren Schicht des Zuschnitts gedehnt und die Fasern der inneren Schicht gestaucht.
Die Dehnung der Fasern der äußeren Schicht nimmt von außen nach innen allmählich ab, und die Kompression der Fasern der inneren Schicht nimmt ebenfalls von innen nach außen allmählich ab.
Wenn die Fasern von der Streckung zur Kompression oder von der Kompression zur Streckung übergehen, muss es eine Faserschicht geben, bei der die Spannung und die Dehnung gleich Null sind und deren Länge vor und nach der Biegung unverändert bleibt.
Diese Schicht bezeichnen wir als die neutrale Schicht. Der Schlüssel zur Berechnung der entfalteten Abmessung des gebogenen Rohlings ist daher die Bestimmung der Position der neutralen Schicht. Die Lage der neutralen Schicht wird unter der Voraussetzung bestimmt, dass das Volumen des Biegeteils und des Rohlings vor und nach der plastischen Verformung gleich sind.
2. Bestimmung des Krümmungsradius ρ der neutralen Schicht
Theoretisch ist die neutrale Schicht aufgrund der ungleichmäßigen Verformung entlang der Dickenrichtung des gebogenen Teils eine parabolische Fläche, aber für Berechnungszwecke wird sie gewöhnlich als Kreisbogenfläche betrachtet. Wenn die Biegeverformung sehr klein ist (r/t >6,5), kann die neutrale Schicht näherungsweise als in der Mitte der Materialdicke liegend betrachtet werden, d. h. der Krümmungsradius der neutralen Schicht ist ρ=r+t/2.
Wenn die Verformung sehr groß ist (r/t≤6,5), wird die Materialdicke dünner, und die Querschnittsverformung ist sehr groß, wie in Abbildung 5-3 dargestellt.
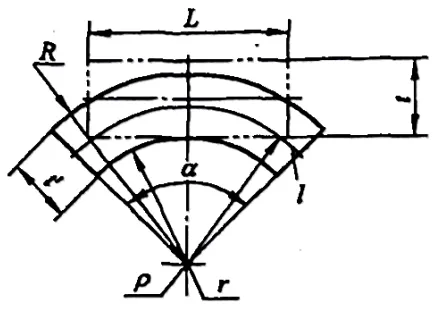
Um die Gleichgewichtsbedingung zu erfüllen, dass die resultierende Kraft aller in dem Abschnitt wirkenden Kräfte gleich Null ist, muss sich die neutrale Schicht zu diesem Zeitpunkt in Richtung der inneren Oberfläche des Materials bewegen.
An dieser Stelle kann der Krümmungsradius der neutralen Schicht unter der Voraussetzung bestimmt werden, dass sich das Volumen während der plastischen Verformung nicht ändert, d. h. das Volumen vor der Biegung: V0=LBt, und das Volumen nach dem Biegen:
V=(R2-r2)α*B'/2.
In der Formel ist B die Breite des Rohlings (mm); B' ist die durchschnittliche Breite des Rohlings nach dem Biegen (mm); α ist der Biegemittelwinkel. Nach dem Prinzip, dass das Volumen vor und nach dem Biegen gleich ist, ergibt sich V0=V, das heißt,
LBt=(R2-r2)α*B'/2, und L=(R2-r2)α*B'/2tB (5-1).
Aus der Nullspannung und -dehnung der neutralen Schicht ergibt sich L=l=αρ, wobei L die Länge vor der Verformung der neutralen Schicht (mm) und l die Länge nach der Verformung der neutralen Schicht (mm) ist.
Setzt man Gleichung (5-1) ein, erhält man ρ=(R2-r2)B'/2tB. Wenn wir R=r+t' in die obige Gleichung einsetzen, erhalten wir eine andere Form der Gleichung ρ=(r/t+η/2)tβη (5-2)wobei β der Breitenfaktor ist, β=B'/B, und im Allgemeinen, wenn ein breites Blech (B>3t) gebogen wird, gilt, dass β=1; η ist der Ausdünnungsfaktor, η=t'/t.
Gleichung (5-2) ist die Formel zur theoretischen Berechnung der Lage der neutralen Schicht. Für die Berechnung muss man η, d. h. die Ausdünnungsregel, kennen. Der Wert von η kann in Tabelle 5-1 nachgeschlagen werden.
Es ist darauf hinzuweisen, dass die Ausdünnungsregel recht komplex ist, dass die Verteilung der neutralen Schicht im Biegebereich nicht gleichmäßig ist und dass die Ausdünnungsregel auch von vielen Faktoren wie dem Biegeverfahren, der Breite des unteren Biegeschlitzes und der Materialdicke abhängt.
Dies führt zu unvermeidbaren Fehlern bei der theoretischen Berechnung der Lage der neutralen Schicht und mindert damit den praktischen Anwendungswert der theoretischen Bestimmungsmethode.
Tabelle 5-1: Verdünnungsfaktor η
| r/t | 0.1 | 0.25 | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | ≥5 |
| η | 0.82 | 0.87 | 0.92 | 0.96 | 0.985 | 0.992 | 0.995 | 0.998 | 1 |
In der Praxis wird in der Regel eine empirische Formel zur Bestimmung der Lage der neutralen Achse verwendet, die einfacher ist als eine theoretische Berechnung, und zwar wie folgt
ρ = r + Kt (5-3)
Wo:
- ρ - Radius der Krümmung der neutralen Achse (mm)
- r - Innenradius der Biegung des Rohmaterials (mm)
- t - Dicke des Materials (mm)
- K - Koeffizient der neutralen Achse (empirisch) Faktor K), siehe Tabelle 5-2
Tabelle 5-2: Empirische Werte des Neutralachsenkoeffizienten K
| r/t | K1 | K2 | ±k |
| 0.3 | 0.2 | 0.23 | 0.04 |
| 0.4 | 0.22 | 0.24 | |
| 0.5 | 0.23 | 0.25 | |
| 0.6 | 0.24 | 0.265 | |
| 0.7 | 0.26 | 0.28 | |
| 0.8 | 0.28 | 0.3 | |
| 1 | 0.31 | 0.32 | |
| 1.2 | 0.32 | 0.33 | |
| 1.3 | 0.33 | 0.34 | |
| 1.5 | 0.35 | 0.36 | |
| 2 | 0.37 | 0.38 | 0.03 |
| 2.5 | 0.38 | 0.39 | |
| 3 | 0.39 | 0.4 | |
| 4 | 0.42 | 0.42 | |
| 5 | 0.44 | 0.44 | 0.02 |
| 6 | 0.46 | 0.46 | |
| 7 | 0.48 | 0.48 | |
| ≥8 | 0.5 | 0.5 |
Anmerkung:
- K1 ist für V- oder U-förmige Biegungen mit einer Oberplatte oder einer Pressplatte geeignet.
- K2 ist für V-förmige Bögen ohne Deckplatte geeignet.
3. Berechnung der Abmessungen des ungefalteten Zuschnitts für mehrere typische Blechbiegungen
Ausgehend von der Definition der neutralen Lage sollte die ungefaltete Abmessung des Zuschnitts der Länge der neutralen Lage entsprechen. Typischerweise wird auf der Grundlage der inneren Biegeradius r des Rohlings werden Biegungen in rund-eckige und nicht rund-eckige Biegungen eingeteilt: Biegungen gelten als rund-eckig, wenn r>0,5t, und als nicht rund-eckig, wenn r<0,5t.
Darüber hinaus werden Biegungen auf der Grundlage der Blechbreite B in breite und schmale Blechbiegungen unterteilt: Wenn die Blechbreite B>3t ist, spricht man von einer breiten Blechbiegung, wenn die Blechbreite B<3t ist, von einer schmalen Blechbiegung.
In der Produktionspraxis sind Biegungen mit rundem Eckradius (r>0,5t) und breiten Blechen (B>3t) am weitesten verbreitet. In Anbetracht der Universalität von Biegungen diskutieren wir hauptsächlich die Berechnung der Abwicklungsmaße für Biegungen mit rundem Eckradius und breiten Blechen während des Biegens.
3.1 Berechnung der Zuschnittabmessungen für Rund-Eck-Bögen (r>0,5t)
Wenn r>0,5t, B>3t, aufgrund der geringen Ausdünnung des Biegeteils und der geringen Querschnittsverformung, kann die Länge des Rohlings nach dem Prinzip bestimmt werden, dass die Länge der neutralen Schicht gleich dem abgewickelten Rohling ist.
Die gängigen Methoden zur Berechnung der Abwicklungsmaße von Rundbögen (r>0,5t) werden unterteilt in: die Berechnung des Biegekoeffizienten und die Berechnung des Biegeabzugswertes.
1. Rund-Eck-Biegungen (r>0,5t) Berechnung des Biegekoeffizienten für ungefaltete Abmessungen:
1) Der Biegekoeffizient ist die Länge des Bogenabschnitts, gemessen entlang der neutralen Schicht der Biegeverformungszone (Biege-R-Abschnitt), wie in Abbildung 5-4 dargestellt.
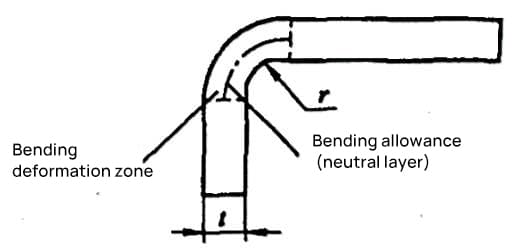
Der Biegekoeffizient wird nach der Formel (5-4) berechnet: x=παρ/180° (5-4)
Dabei ist ρ der Krümmungsradius der neutralen Schicht (mm).
2) Abbildung 5-5 zeigt ein Beispiel für die Notation der Abmessungen für die Berechnung des Biegekoeffizienten der ungefalteten Abmessungen des Rohlings, und die Formel für die Berechnung des Biegekoeffizienten der ungefalteten Abmessungen des Rohlings lautet wie folgt.

a) φ > 90° b) φ≤90
L=a+b+x (5-5)
Setzt man Gleichung (5-3) in Gleichung (5-4) ein, erhält man die Formel für den Biegekoeffizienten:
x=πα(r+Kt)/180° (5-6)
Setzt man Gleichung (5-6) in Gleichung (5-5) ein, erhält man die Formel für die Berechnung der ungefalteten Größe des gebogenen Rohlings:
L=a+b+πα(r+Kt)/180° (5-7)
Wo:
- L - Die ungefaltete Größe des Rohlings (mm);
- K - Koeffizient für den K-Faktor, dessen Wert in Tabelle 5-2 angegeben ist;
- α - Der zentrale Biegewinkel, sein Verhältnis zum Winkel des gebogenen Teils ist α=180°-φ;
- r - Der Biegeradius der inneren Schicht des Rohlings (mm);
- t - Die Dicke des Materials (mm);
- a, b - Die Längen der geraden Teile des Bauteils (mm).
2. Berechnung des Biegeabzugs für die abgewickelte Größe eines Biegeteils mit abgerundeten Ecken (r>0,5t)
1) Der Biegeabzug (auch bekannt als Korrekturwert für den R-Teil) ist die Differenz zwischen dem doppelten R der Biegeverformungszone (dem R-Teil der Biegung) und dem Biegekoeffizienten, wie in Abbildung 5-6 dargestellt.

Der Biegeabzug (Korrekturwert für den R-Anteil) wird nach Gleichung (5-8) berechnet:
y = 2R-παr/180° (5-8)
2) Abbildung 5-7 zeigt ein Beispiel für eine Bemaßung zur Berechnung des Biegeabzugs für die ungefaltete Größe des Zuschnitts. Der Biegeabzug y wird nach der folgenden Formel berechnet:
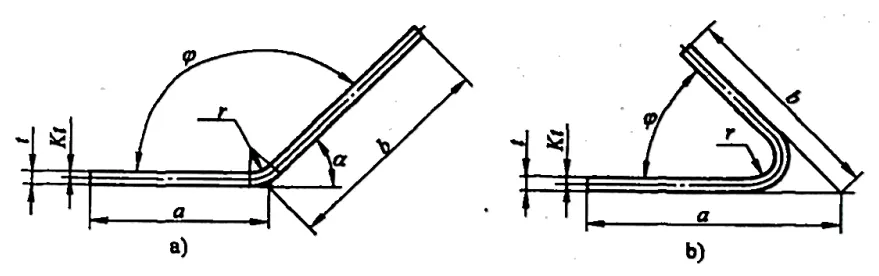
a)90°<φ≤165° b)φ≤90°
①Wenn φ ≤ 90°:
R=(r+t)/tan(φ/2)
Setzt man die obige Formel und Formel (5-3) in Formel (5-8) ein, erhält man den Biegeabzug (d. h. den Korrekturwert des R-Anteils) für eine Biegung φ≤90° (siehe Abbildung 5-7b):
y=2(r+t)/tan(φ/2)-πα(r+Kt)/180° (5-9)
②Wenn 90°<φ≤165°:
R=(r+t)tan[(180°-φ)/2]
Setzt man die obige Formel und Formel (5-3) in Formel (5-8) ein, erhält man den Biegeabzug (d. h. den Korrekturwert des R-Anteils) für eine Biegung 90°<φ≤165° (siehe Abbildung 5-7a):
y=2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180° (5-10)
③Wenn 165°<φ≤180°:
y≈0
3) Die Formel zur Berechnung des Biegeabzugswerts für die Rohteilgröße des in Abbildung 5-7 dargestellten Teils lautet:
L=a+b-y (5-11)
Wenn φ≤90° ist, erhält man durch Einsetzen der Formel (5-9) in die Formel (5-11) die Formel für die Berechnung des Biegeabzugswerts der Rohteilgröße wie folgt:
L=a+b-[2(r+t)/tan(φ/2)-πα(r+Kt)/180°] (5-12)
Wenn 90°<φ≤165° ist, erhält man durch Einsetzen der Formel (5-10) in die Formel (5-11) die Formel zur Berechnung des Biegeabzugswerts der Zuschnittgröße wie folgt:
L=a+b-[2(r+t)tan[(180°-φ)/2]-πα(r+Kt)/180°] (5-13)
③Wenn 165°<φ≤180°:
L≈a+b (5-14)
Wo,
- y - Biegeabzug (mm)
- L - Rohlingsgröße des Teils (mm)
- r - Innerer Biegeradius des Rohlings (mm)
- t - Dicke des Materials (mm)
- α - Biegemittenwinkel, seine Beziehung zum Biegewinkel ist α=180°-φ
- a, b - Kantenlängen des Teils (mm) bis zum Biegescheitelpunkt.
3. Berechnung der Rohlingsgröße für mehrwinklige Biegungen
Bei mehrwinkligen Biegungen ist die Größe des Rohlings die Summe aus dem R-Teil und den Längen der geraden Kanten.
1) Berechnung der Größe des gebogenen Rohlings mit mehreren Winkeln anhand des Biegekoeffizienten:
L=l1+l2+...+ln+1+nx (5-15)
Wo l1, l2...ln+1 sind die Längen der geraden Teile jeder Kante des Teils (mm);
n ist die Anzahl der Biegungen R.
2) Multi-angle bend blank Größe Berechnung durch die Biegung Abzug:
L=l1+l2+...+ln+1-ny (5-16)
Wo l1, l2...ln+1 sind die Längen der Kanten des Teils (mm) bis zum Biegescheitelpunkt;
n ist die Anzahl der Biegungen R.
Beispiel 5-1: Berechnen Sie die Zuschnittgröße für die in Abbildung 5-8 dargestellte Biegung.
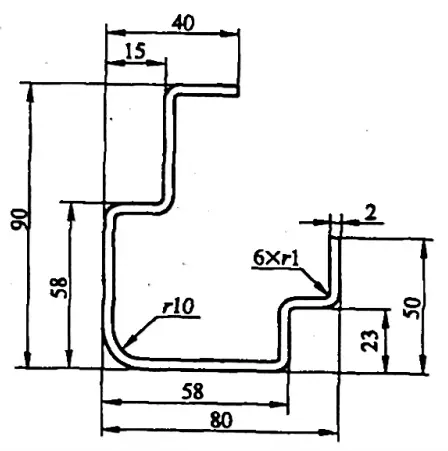
Lösung 1: Berechnen Sie die Größe des Rohlings anhand des Biegekoeffizienten.
Siehe Anhang A: Wenn der Winkel des Biegeteils φ=90°, die Dicke t=2mm und der Radius r=10mm ist, beträgt der Biegekoeffizient 2,68mm;
Wenn der Winkel des Biegeteils 90°, die Dicke t=2mm und der Radius r=10mm beträgt, ist der Biegekoeffizient x2=16,9mm.
Aus den Gleichungen (5-5) und (5-15) errechnet sich das Flachmaß des Rohlings für das gebogene Stück wie folgt:
L= [(40-15-2-1) + (90-58-2-2×1) + (15-2-2×1) +2(58-2×2-10-1) + (23-2-2×1) + (80-58-2-2×1) + (50-23-2-1) + 6×2,68 + 16,9]mm
= (22+28+11+86+19+18+24+16.08+16.9)mm
= 240,98 mm.
Lösung 2: Berechnen Sie die flache Größe des Rohlings anhand des Biegeabzugswertes.
Siehe Anhang C: Für eine Biegung mit einem Winkel φ=90°, einer Dicke t=2mm und einem Radius r=1mm beträgt der Korrekturwert für den R-Schnitt y1=3,32mm; für eine Biegung mit einem Winkel φ=90°, einer Dicke t=2mm und einem Radius r=10mm beträgt der Korrekturwert für den R-Schnitt y2=7,1mm.
Die Rohgröße des gebogenen Teils kann aus den Gleichungen (5-11) und (5-16) ermittelt werden:
L= [(40-15) + (90-58+2) + (15+2) + 2×58 + (23+2) + (80-58+2) + (50-23) - 6×3,32 - 7,1] mm
= (25+34+17+116+25+24+27-19,92-7,1) mm
= 240,98 mm
Beispiel 5-2: Berechnen Sie die Rohgröße des in Abbildung 5-9 gezeigten Biegeteils.
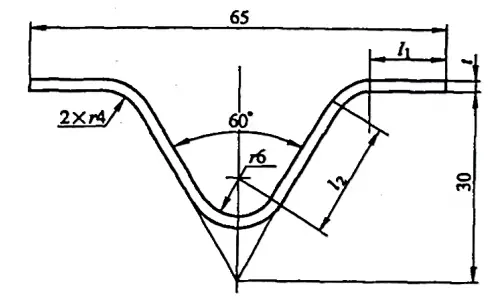
Lösung: Berechnen Sie die Rohgröße anhand des Biegekoeffizienten.
Die Formel zur Berechnung der Rohteilabmessungen des Biegeteils aus den Gleichungen (5-5) und (5-15) lautet:
L=2l1+2l2+2x1+x2
wobei l1 = [32,5 - (30tan30°+4tan30°)] mm = 12,87 mm
und l2 = [(30/cos30°) - (8/tan30°+4tan30°)] mm = 18,47 mm
Siehe Anhang A: Wenn der Biegewinkel φ=120°, t=2mm, r=4mm ist, beträgt der Wert des Biegefaktors x1=4,98mm; bei einem Biegewinkel φ=60°, t=2mm, r=6mm beträgt der Biegefaktorwert x2=14,16 mm.
Setzt man diese Werte in die Formel ein, so ergibt sich die ungefaltete Länge des Rohlings als L= (2×12,87 + 2×18,47 + 2×4,98 + 14,16) mm = 86,8 mm.
Es ist zu beachten, dass bei einfacheren Biegungen mit geringeren Genauigkeitsanforderungen die Abmessungen des abgewickelten Rohlings direkt berechnet werden können. Bei komplexeren Biegungen oder solchen mit höheren Genauigkeitsanforderungen müssen die Form und die Abmessungen des abgewickelten Rohlings jedoch wiederholt geprüft und kontinuierlich überarbeitet werden, um die Form und die Abmessungen des Rohlings zu bestätigen.
3.2 Berechnung der Rohteilabmessungen für scharfkantige Bauteile (r<0,5t)
Wenn der Biegeradius r eines Bauteils kleiner als 0,5t ist, spricht man von einer scharfen Biegung. Die Berechnung des Rohteilentwicklungsmaßes für solche Bauteile basiert auf dem Prinzip der Volumenkonsistenz vor und nach dem Biegen.
Bei scharfen Biegungen ist der Verformungsprozess aufgrund der starken Ausdünnung des Materials an der Biegung äußerst komplex, was eine genaue Berechnung der Rohteilabmessungen erschwert. Daher müssen die berechneten Rohteilentwicklungsmaße auf der Grundlage empirischer Daten oder durch Probebiegen korrigiert werden.
Die Berechnungsformel für die Rohteilabmessungen von scharfkantigen Bauteilen (r<0,5t, φ=90°) ist in Tabelle 5-3 zu finden.
Tabelle 5-3 Berechnungsformel für Rohteilabmessungen von scharfkantigen Biegeteilen (r<0,5t, φ=90°) (Einheit: mm)
| Seriennummer | Biegeeigenschaften | Schematische Darstellung | Formel |
| 1 | Eine Ecke biegen. |  | L=a+b+0,4t |
| 2 | Glätten Sie es. |  | L=a+b-0,43t |
| 3 | Biegen Sie zwei Ecken auf einmal. | 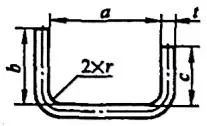 | L=a+b+c+0,6t |
| 4 | Biegen Sie drei Ecken gleichzeitig. | 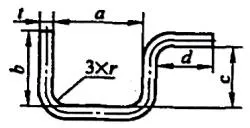 | L=a+b+c+d+0,75t |
| 5 | Biegen Sie im ersten Fall zwei Ecken und im zweiten Fall eine weitere Ecke. | L=a+b+c+d+t | |
| 6 | Biegen Sie vier Ecken gleichzeitig. | 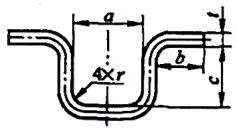 | L=a+2b+2c+1,2t |
| 7 | In zwei Fällen zu vier Ecken biegen. | L=a+2b+2c+1,2t |
3.3 Berechnung der Abwicklungsmaße für Scharnierbiegeteile
Für Scharniertyp Biegeteile mit r= (0,6~3,5)t (siehe Abbildung 5-10), verläuft der Bördelvorgang in der Regel nach dem in Abbildung 5-11 dargestellten Muster. Während des Bördelns nimmt die Dicke des Blechs zu und die neutrale Schicht verschiebt sich nach außen. Die abgewickelten Abmessungen der Platine können näherungsweise mit der folgenden Formel berechnet werden:
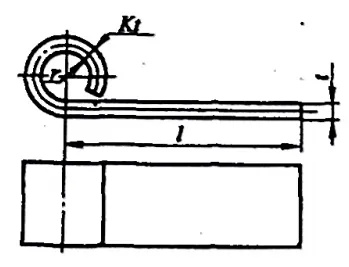
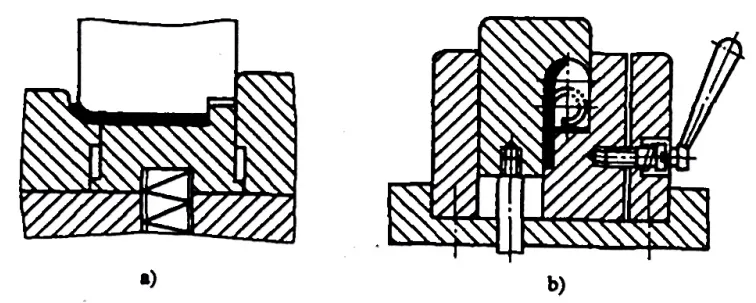
- a) Erste Operation
- b) Zweite Operation
L=l+1,57π(r+Kt)+r
Wo:
- L - Maße des Rohlings im ungefalteten Zustand (mm);
- l - Länge des geraden Segments (mm);
- r - Innerer Biegeradius des Rohlings (mm);
- K - Verdrängungskoeffizient der neutralen Schicht. Wenn r/t=0,5~1,8 ist, wird K normalerweise mit 0,5~0,70 angenommen (je kleiner der r/t-Wert, desto größer der K-Wert; umgekehrt, desto kleiner der K-Wert). Er kann auch gemäß Tabelle 5-4 gewählt werden.
Tabelle 5-4 Verschiebungskoeffizient der neutralen Schicht für gelenkige Biegeteile
| r/t | ≥0.5~0.6 | >0.6~0.8 | >0.8~1 | >1~1.2 | >1.2~1.5 | >1.5~1.8 | >1.8~2 | >2~2.2 | >2.2 |
| K | 0.76 | 0.73 | 0.7 | 0.67 | 0.64 | 0.61 | 0.58 | 0.54 | 0.5 |