Ever wondered how to calculate the weight of steel for your next DIY project or construction task? Whether you’re dealing with steel rods, bars, plates, or sheets, understanding how to accurately determine their weight is crucial. This guide will demystify the process with step-by-step instructions tailored for beginners. We’ll start by introducing the basic concept of steel weight calculation, including the all-important density of steel. Then, we’ll dive into specific formulas for various steel shapes, such as the D²/162 formula for bars and the volume-based formula for plates and sheets. By the end of this article, you’ll be well-equipped with practical tips and examples to ensure your calculations are precise and reliable. Ready to become a steel weight calculation pro? Let’s get started!
Introduction to Steel Weight Calculation
Importance of Calculating Steel Weight
Calculating steel weight is essential in industries like construction, manufacturing, and engineering. Understanding how to determine steel weight is crucial for project planning, cost estimation, ensuring structural safety, optimizing material usage, avoiding wastage, and adhering to load-bearing requirements.
Basic Concept of Steel Weight Calculation
The weight of steel depends on two main factors:
- Volume of the steel piece – This refers to the amount of space the steel occupies.
- Density of the steel alloy – This is the mass per unit volume of the steel.
The general formula for calculating steel weight is:
Weight is typically measured in kilograms (kg), volume in cubic meters (m³), and density in kilograms per cubic meter (kg/m³).
Understanding Steel Density
Steel density can vary slightly depending on the type and composition of the alloy. Here are some common steel densities:
- Mild steel: approximately 7,870 kg/m³
- Carbon steel: approximately 7,850 kg/m³
- Stainless steel: around 8,030 kg/m³
Knowing the exact density of the steel type you are using is crucial because even small variations can significantly affect the weight calculation, especially for large volumes.
Measuring Dimensions
To calculate the volume of a steel piece, accurate measurement of its dimensions is necessary. The method for calculating volume depends on the shape of the steel object:
Rectangular or square plates and bars:
Volume=Length×Width×ThicknessRound bars or rods:
Volume=π/4×(Diameter)2×Length
Make sure all measurements are in the same units (meters for length, width, thickness, and diameter) to match the density units.
Practical Steps for Steel Weight Calculation
- Identify the steel type and note its density.
- Measure the dimensions of the steel piece accurately.
- Calculate the volume using the appropriate formula for the shape.
- Multiply the volume by the steel density to obtain the weight.
Example Calculations
Example 1: Rectangular Steel Plate
- Length: 2 meters
- Width: 1 meter
- Thickness: 0.005 meters (5 mm)
- Density: 7,850 kg/m³ (mild steel)
Example 2: Round Steel Bar
- Diameter: 0.05 meters (50 mm)
- Length: 3 meters
- Density: 7,850 kg/m³ (mild steel)
These examples demonstrate how to apply formulas for different shapes to achieve accurate steel weight calculations.
Understanding the Density of Steel
Steel density is the mass per unit volume of steel, and understanding this property is essential for many applications. It plays a crucial role in weight calculations, structural engineering, and material selection, helping engineers and manufacturers ensure accurate material estimates, optimize designs, and maintain structural integrity.
The standard density of steel is approximately 7,850 kg/m³, though it can vary slightly based on its composition, such as the presence of elements like manganese, nickel, or chromium. For example, stainless steel typically has a density range of about 7,750 to 8,050 kg/m³. To calculate the density of steel, follow these steps:
Measure the Mass: Begin by measuring the mass of the steel sample using a calibrated scale. Record the mass in kilograms (kg) or grams (g), depending on the scale’s precision.
Determine the Volume: The method for determining the volume depends on the shape of the steel object:
- For regular shapes like rectangular prisms, use geometric formulas such as length × width × height.
- For irregular shapes, submerge the steel in water and measure the amount of water displaced to find the volume.
Apply the Density Formula: Use the formula density = mass / volume. Ensure the units are consistent; for example, if the mass is in kilograms and the volume is in cubic meters, the density will be in kilograms per cubic meter (kg/m³).
Knowing the density and volume of steel allows you to calculate its mass using the formula mass = density × volume. For instance, if a steel beam has a volume of 2 cubic meters and a density of 7,850 kg/m³, the mass would be:
Understanding the density of steel is crucial for accurate weight calculations and material selection in various industrial applications. By measuring mass and volume and applying the density formula, professionals can achieve precise and reliable results in their projects.
Steel Weight Formulas for Different Shapes
Overview of Various Steel Shapes
Steel is available in many shapes, each with its own specific weight calculation formula. Understanding these shapes and their corresponding formulas is essential for precise weight calculations in construction, manufacturing, and engineering projects.
Steel Bars and Rods
For cylindrical steel rods, the weight can be calculated using the following formula:
where ‘d’ is the diameter, ‘l’ is the length, and ‘density’ is typically 7850 kg/m³. Alternatively, a simplified formula often used for quick calculations in metric units is:
In this formula:
- d is in millimeters (mm)
- l is in meters (m)
Steel Plates
The weight of rectangular steel plates can be calculated using the formula:
For practical purposes, this is often simplified to:
where ‘t’ is the thickness in millimeters, and ‘w’ and ‘l’ are in meters.
Steel Tubes and Pipes
For steel tubes and pipes, use the formula:
A simplified version commonly used is:
where ‘O.D.’ is the outer diameter, ‘W.T.’ is the wall thickness, and ‘l’ is the length.
Hexagonal and Octagonal Shapes
For hexagonal steel bars, the weight is calculated as:
For octagonal steel bars:
where ‘d’ is the side length and ‘l’ is the length of the bar.
Explanation of the D²/162 Formula for Steel Bars
Detailed Breakdown of the D²/162 Formula
The D²/162 formula is a simplified method used to calculate the weight of steel bars per meter. This formula is particularly useful in the construction industry for quickly estimating the weight of steel bars, which are commonly used in various structural applications.
Understanding the Components of the Formula
To understand how the D²/162 formula works, it’s important to break down its components:
- Diameter of the Steel Bar (D): This is the diameter of the steel bar measured in millimeters (mm).
- Constant (162): This constant is based on the density of steel and various conversion factors to make the calculation easier.
Derivation of the Formula
The formula is derived from the basic principle of calculating the weight of an object using its volume and density. For a circular steel bar, the cross-sectional area (A) is given by:
Area of Steel Bar:
A=πD2/4
where ( D ) is the diameter of the bar.Volume of Steel Bar: Given the steel bar’s length (L) is 1 meter, the volume (V) is:
V=A×L=πD2/4×1Density of Steel: The density (ρ) of steel is approximately 7850 kg/m³.
Weight of Steel Bar: Therefore, the weight (W) of the steel bar can be calculated as:
W=V×ρ=πD2/4×7850
Simplifying further:
W=(πD2×7850)/4Conversion to Kilograms per Meter: Since the diameter is in millimeters, we need to convert it into meters by dividing by 1000. The simplified formula becomes:
W=D2×((3.14×7850)/(4×10002))
W=D2×0.00616225≈D2/162
Importance and Applications
The D²/162 formula is popular because it quickly estimates the weight of steel bars without complicated calculations. This is particularly useful for:
- Construction Planning: Helps in estimating the weight of steel required for projects.
- Cost Estimation: Assists in budgeting by providing an approximation of the material costs.
- Load Calculations: Ensures structural integrity by helping calculate the load-bearing capacity.
Practical Example
To illustrate how to use the D²/162 formula, consider the following example:
- Diameter of Steel Bar: 20 mm
- Length of Steel Bar: 10 meters
Calculate Weight per Meter:
Weight per Meter=202/162=400/162≈2.47kg/mCalculate Total Weight:
Total Weight=2.47×10=24.7kg
This example demonstrates the simplicity and efficiency of the D²/162 formula in calculating the weight of steel bars.
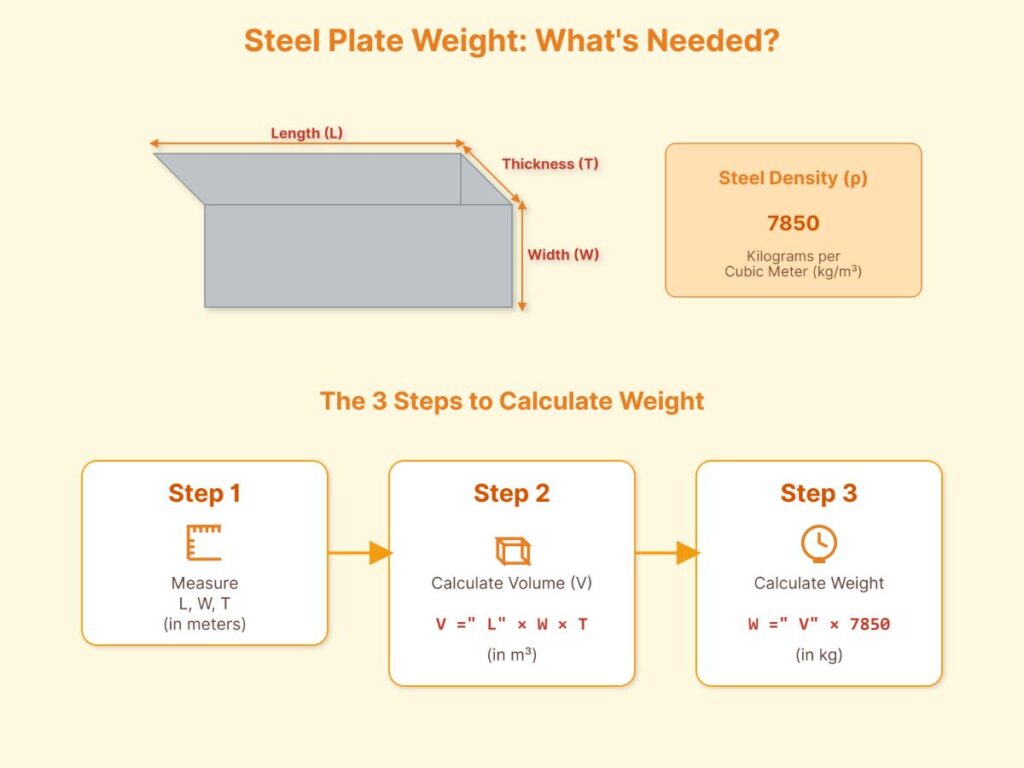
Calculating the Weight of Steel Plates
Accurately measure the steel plate’s thickness, width, and length to find its volume.
Calculate the volume by multiplying the plate’s thickness, width, and length; for instance, if the thickness is 10 mm, the width is 1.5 m, and the length is 3 m:
Steel density varies slightly by type:
- Carbon Steel: approximately 7,850 kg/m³
- Mild Steel: approximately 7,870 kg/m³
- Stainless Steel: 7,900–8,000 kg/m³
Multiply the volume (0.045 m³) by the density of steel (7,850 kg/m³) to get the weight:
For multiple plates, multiply the weight of one plate by the total number of plates. For example, if each plate weighs 3.148 kg and you have 5 plates:
Always ensure all measurements are in the same system (metric or imperial) before calculating. For calculations in inches and pounds, convert thickness, width, and length to inches and use the steel density typically around 0.284 lb/in³ for carbon steel. Manufacturing tolerances and surface coatings can slightly affect the actual weight, so consider these factors when precision is critical.
Calculating the Weight of Steel Rods and Bars
Measuring the Dimensions
To calculate the weight of steel rods and bars, start by measuring their dimensions accurately.
Diameter (D)
Use calipers or a tape measure to determine the diameter of the steel rod. Record this measurement in millimeters (mm) for metric calculations or inches (in) for imperial calculations.
Length (L)
Measure the total length of the rod in meters (m) for metric calculations or feet (ft) for imperial calculations. Ensure the measurement is precise for accurate weight estimation.
Applying the D²/162 Formula (Metric Units)
To calculate the weight of steel rods and bars in metric units, a simplified formula can be used, which accounts for the density of steel and necessary unit conversions:
- D = Diameter in millimeters (mm)
- L = Length in meters (m)
- 162 = Constant that incorporates π/4, steel density, and unit conversions
Example Calculation
Consider a steel rod with a diameter of 12 mm and a length of 5 meters; to calculate its weight, apply the formula as follows:
Formula for Steel Shapes (Imperial Units)
For steel shapes in imperial units, use the following formula to determine the weight. Multiply the length (in feet), width (in feet), thickness (in feet), and the density of steel (490 lb/ft³):
Example Calculation
For a square steel bar with a side length of 4 inches (0.33 ft) and a length of 8 feet:
Key Considerations
Density Variations
Check the type of steel, as different types have slightly varying densities. For example, the density of carbon steel is approximately 7850 kg/m³ or 490 lb/ft³. Ensure the correct density value is applied in calculations.
Shape-Specific Formulas
Different shapes of steel require specific formulas for accurate weight calculations:
- Round Bars: Use the D²/162 formula per meter for metric calculations.
- Flat Bars: Calculate the cross-sectional area (width × thickness) and multiply by length and density.
Unit Consistency
Ensure all measurements match the units required by the formula being used. Consistency in units is crucial for accurate weight calculations.
Practical Tools
Online Calculators
Several online tools are available to simplify weight calculations for steel rods and bars. For quick results, consider using calculators from reputable sources such as Eaton Steel or Omnicalculator.
Manual Checks
For critical projects, it’s important to cross-verify automated results using the formulas provided. This ensures precision and reliability in your weight calculations.
Calculating the Weight of Steel Sheets
To calculate the weight of a steel sheet, you need to know its length, width, and thickness.
Calculating the Volume of the Steel Sheet
Multiply the length, width, and thickness to find the volume (V).
For example, if the steel sheet is 2 meters long, 1 meter wide, and 0.01 meters (10 mm) thick:
Using the Density of Steel
The density of mild steel is about 7,870 kg/m³.
Calculating the Weight of the Steel Sheet
To find the weight, multiply the volume by the density of steel:
Using the example volume of 0.02 m³:
Calculating the Weight for Multiple Sheets
If you have multiple sheets, multiply the weight of one sheet by the number of sheets. For example, 5 sheets would weigh:
Example Calculation
For a steel sheet that is 2 m long, 1 m wide, and 0.01 m thick:
Using a density of 7,870 kg/m³:
| Step | Formula/Action | Example (Metric) |
|---|---|---|
| Measure dimensions | Length, Width, Thickness | 2 m, 1 m, 0.01 m |
| Calculate volume | (V=L×W×T) | (0.02m3) |
| Use steel density | Density ≈ 7,870 kg/m³ | — |
| Calculate weight | Weight = Volume × Density | 157.4 kg |
| Multiply if needed | Total Weight = Weight × Number of sheets | 787 kg for 5 sheets |
Using these steps, you can quickly and accurately calculate the weight of steel sheets for any construction, fabrication, or purchasing needs.
Steel Volume Calculation
Determining the volume of steel is crucial for calculating its weight. The method for calculating the volume depends on the shape of the steel object. Below are the methods for different steel shapes:
Steel Plates and Sheets
Steel plates and sheets are typically rectangular. To calculate their volume, measure the length, width, and thickness.
Formula:
Let’s take a look at how to find the volume of a steel plate with specific dimensions:
- Length: 3 meters
- Width: 1.5 meters
- Thickness: 0.01 meters (10 mm)
Calculation:
Steel Rods and Bars
Steel rods and bars are typically cylindrical. To calculate their volume, measure the diameter and length.
Formula for a Cylinder:
First, calculate the radius by dividing the diameter by 2:
Then, use the formula for the cylinder volume:
Let’s take a look at how to find the volume of a steel rod with specific dimensions:
- Diameter: 0.02 meters (20 mm)
- Length: 10 meters
Calculation:
Steel Beams and Structures
Steel beams and other structural shapes can have complex geometries. For simplicity, these are often treated as rectangular prisms. Measure the length, width, and height.
Formula:
Let’s take a look at how to find the volume of a steel beam with specific dimensions:
- Length: 5 meters
- Width: 0.2 meters
- Height: 0.1 meters
Calculation:
Key Points to Remember
- Ensure all dimensions are measured accurately for precise volume calculations.
- Use the appropriate formula based on the shape of the steel object.
- Ensure that all units are consistent (e.g., meters for volume and kilograms per cubic meter for density).
By following these methods and examples, you can accurately calculate the volume of different steel shapes, which is the first step in determining their weight.
Unit Conversions in Steel Weight Calculation
Understanding unit conversions is essential for accurately calculating the weight of steel, especially when dealing with different units of measurement. Converting units ensures consistency and accuracy in calculations, which is vital for engineers, manufacturers, and construction professionals.
Common Units and Their Conversions
Length Conversions
Length measurements are often needed in both metric and imperial units; here are some common conversions:
Meters to Feet:
1meter=3.2808feetCentimeters to Inches:
1centimeter=0.3937inchesMillimeters to Inches:
1millimeter=0.03937inches
Mass Conversions
Mass is often measured in both kilograms and pounds. Here are the conversions:
Kilograms to Pounds:
1kilogram=2.20462poundsGrams to Pounds:
1gram=0.00220462pounds
Density Conversions
Density is usually given in kilograms per cubic meter (kg/m³) or pounds per cubic foot (lb/ft³). Here are the conversions:
- Kilograms per Cubic Meter to Pounds per Cubic Foot:
1kg/m3=0.06242796lb/ft3
Practical Examples
Example 1: Converting Length
If a steel rod is 2 meters long and you need to convert this length to feet:
2meters×3.2808feet/meter=6.5616feet
Example 2: Converting Mass
If a steel plate weighs 50 kilograms and you need to convert this weight to pounds:
Example 3: Converting Density
If the density of steel is 7850 kg/m³ and you need to convert this density to lb/ft³:
Ensuring Accurate Conversions
- Identify the Units: Identify the units of the given measurements and the units you need.
- Use Conversion Factors: Apply the appropriate conversion factors based on the units involved.
- Check Consistency: Ensure all measurements are in the same unit system before performing calculations.
Conversion Tools
Use online conversion calculators or reference tables to simplify the process. These tools quickly and accurately convert between units, saving time and reducing errors.
Practical Tips for Accurate Steel Weight Calculation
Understand the Basic Formula for Steel Weight
The fundamental formula to calculate the weight of steel is:
For example, for plates and sheets, if the dimensions are in inches and the density is in pounds per cubic inch, the formula can be simplified to:
Weight (lbs)=Width (in)×Length (in)×Thickness (in)×0.2836
where 0.2836 lb/in³ is the density of mild steel.
For steel bars or rods, the formula is:
Weight=π/4×d2×L×ρ
where ( d ) is the diameter, ( L ) is the length, and ( ρ ) is the density of steel (usually 7850 kg/m³).
For quick estimation, use the formula:
Weight (kg)=(d2×L)/162
where ( d ) is in millimeters and ( L ) is in meters.
Measure Steel Dimensions Accurately
- Use precise tools like calipers or a tape measure to obtain the width, length, thickness, or diameter of the steel piece.
- Ensure measurements are taken in the correct units (inches or millimeters) as required by the formula.
- For irregular shapes, break them down into simpler shapes, measure each part, and calculate their weights individually.
Know the Steel Density for Your Material
The density of steel can vary depending on the alloy type. Here are some common densities (in kg/m³):
- Mild Steel: 7870
- Carbon Steel: 7840
- Stainless Steel: 8030
Using the correct density value for your specific steel type ensures more accurate results.
Calculate Volume Correctly
For plates or sheets, calculate volume as Width × Length × Thickness. For rods, bars, or tubes, use the formula Volume = Cross-sectional area × Length.
Ensure that the units for volume and density match (e.g., cubic meters and kg/m³ or cubic inches and lb/in³) to avoid calculation errors.
Use Weight Calculators for Convenience and Accuracy
Using online steel weight calculators can save time and minimize errors. Simply input the dimensions and select the steel type for an automatic calculation. These tools are especially useful for multiple pieces or complex shapes.
Double-Check Units and Conversions
- Verify that all measurements (length, width, thickness, diameter) are in the same unit system (metric or imperial).
- Convert units if necessary before applying formulas to avoid mistakes. For example, 1 inch = 25.4 mm and 1 lb = 0.4536 kg.
Example Calculation for a Steel Plate
Suppose you have a steel plate measuring 48 inches long, 24 inches wide, and 0.5 inches thick:
Weight=48×24×0.5×0.2836=164.45lbs
To convert to kilograms:
164.45lbs×0.4536=74.6kg
Frequently Asked Questions
Below are answers to some frequently asked questions:
What is the formula to calculate the weight of steel?
To calculate the weight of steel, the formula you use depends on the shape and dimensions of the steel piece.
For flat steel sheets or plates, you can use the following formula:
Here, the width, length, and thickness are measured in inches, and the constant 0.2836 represents the density factor of steel in pounds per cubic inch (lb/in³). This formula gives the weight in pounds (lbs).
For steel rods or bars with a circular cross-section, the weight can be calculated using the simplified empirical formula:
where ( d ) is the diameter in millimeters (mm). This is a quick and widely used formula to estimate the weight of steel rods.
In general, the density of steel, which is typically 7850 kg/m³, is used in these calculations to convert the volume of the steel piece to its weight. By using the appropriate formula for the specific shape, you can accurately determine the weight of steel for various applications.
How do you calculate the weight of a steel rod or bar?
To calculate the weight of a steel rod or bar, you can use the formula:
where:
- D is the diameter of the rod/bar in millimeters (mm)
- L is the length of the rod/bar in meters (m)
- 162 is a constant derived from the density of steel (7850 kg/m³) and unit conversions.
Here’s a step-by-step process:
- Measure the diameter (D) of the steel rod/bar in millimeters.
- Measure the length (L) of the steel rod/bar in meters.
- Square the diameter (D²).
- Multiply the squared diameter (D²) by the length (L).
- Divide the result by 162 to get the weight in kilograms.
For example, if you have a steel rod with a diameter of 12 mm and a length of 5 meters:
This formula provides a simple and practical way to estimate the weight of steel rods and bars commonly used in construction and engineering.
How to calculate the weight of a steel plate or sheet?
To calculate the weight of a steel plate or sheet, you need to know its dimensions and the density of the steel. The density of steel is typically 7850 kg/m³. Follow these steps for an accurate calculation:
Measure the Dimensions: Determine the length (L), width (W), and thickness (T) of the steel plate. Ensure all measurements are in the same unit (e.g., meters).
Calculate the Volume: Multiply the length, width, and thickness to get the volume in cubic meters (m³).
Volume=L×W×TCalculate the Weight: Multiply the volume by the density of the steel.
Weight=Volume×Density
Using the standard density of 7850 kg/m³:
Weight (kg)=Volume (m³)×7850kg/m³
Example Calculation:
For a steel plate with dimensions 2 meters by 1 meter and a thickness of 0.01 meters (1 cm):
By following these steps, you can accurately determine the weight of any steel plate or sheet.
What is the density of steel used in weight calculations?
The density of steel used in weight calculations is typically 7850 kilograms per cubic meter (kg/m³). Density is a measure of mass per unit volume and is crucial for determining the weight of steel in various applications such as construction and manufacturing. By knowing the density, you can apply the formula Weight = Volume x Density to calculate the weight of any steel object, provided you have its volume. This standard value ensures accuracy and consistency in weight calculations, which are essential for cost estimation, structural integrity, and logistics planning.
Why is the constant 162 used in the steel weight formula?
The constant 162 is used in the steel weight formula to simplify the calculation of the weight of steel bars or rods. The exact formula to calculate the weight ( W ) of a cylindrical steel rod is:
where ( d ) is the diameter in meters, ( l ) is the length in meters, and ( ρ ) is the density of steel (approximately 7850 kg/m³). However, this formula can be complex to use directly, especially when the diameter is given in millimeters and length in meters.
To make calculations easier, the formula is simplified by incorporating the physical properties of steel and unit conversions into a constant:
Here, ( d ) is in millimeters, ( l ) is in meters, and ( W ) is in kilograms. The constant 162 comes from evaluating the expression:
This approximation accounts for the steel’s density and the conversion from millimeters to meters, making it practical and easy to use in quick estimations of steel weight.
